121 200304 LK Math Ue7

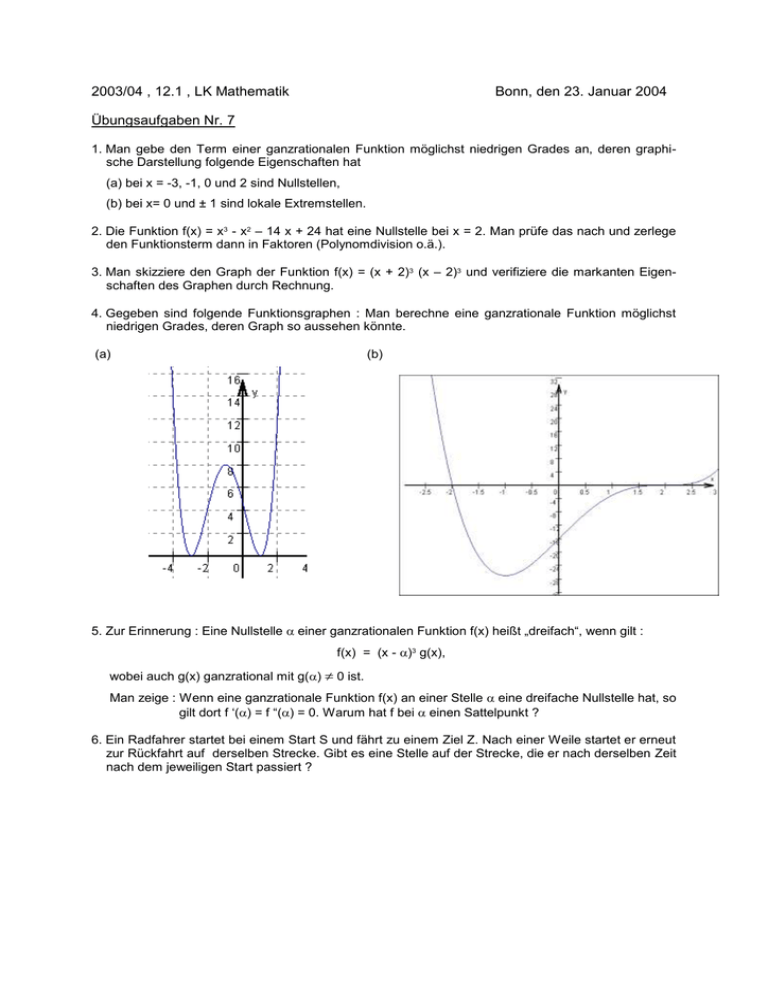
2003/04 , 12.1 , LK Mathematik
Bonn, den 23. Januar 2004
Übungsaufgaben Nr. 7
1. Man gebe den Term einer ganzrationalen Funktion möglichst niedrigen Grades an, deren graphische Darstellung folgende Eigenschaften hat
(a) bei x = -3, -1, 0 und 2 sind Nullstellen,
(b) bei x= 0 und ± 1 sind lokale Extremstellen.
2. Die Funktion f(x) = x3 - x2 – 14 x + 24 hat eine Nullstelle bei x = 2. Man prüfe das nach und zerlege
den Funktionsterm dann in Faktoren (Polynomdivision o.ä.).
3. Man skizziere den Graph der Funktion f(x) = (x + 2)3 (x – 2)3 und verifiziere die markanten Eigenschaften des Graphen durch Rechnung.
4. Gegeben sind folgende Funktionsgraphen : Man berechne eine ganzrationale Funktion möglichst
niedrigen Grades, deren Graph so aussehen könnte.
(a)
(b)
5. Zur Erinnerung : Eine Nullstelle  einer ganzrationalen Funktion f(x) heißt „dreifach“, wenn gilt :
f(x) = (x - )3 g(x),
wobei auch g(x) ganzrational mit g()  0 ist.
Man zeige : Wenn eine ganzrationale Funktion f(x) an einer Stelle  eine dreifache Nullstelle hat, so
gilt dort f ‘() = f “() = 0. Warum hat f bei  einen Sattelpunkt ?
6. Ein Radfahrer startet bei einem Start S und fährt zu einem Ziel Z. Nach einer Weile startet er erneut
zur Rückfahrt auf derselben Strecke. Gibt es eine Stelle auf der Strecke, die er nach derselben Zeit
nach dem jeweiligen Start passiert ?