10.10.2011 - TU Bergakademie Freiberg

194
Numerik I
5
Interpolation und numerische Approximation
5.1 Polynominterpolation
5.2 Spline-Interpolation
5.3 Diskrete Fourier-Transformation
5.4 Schnelle Fourier-Transformation (FFT)
5.5 Eine Anwendung
5 Interpolation und numerische Approximation
TU Bergakademie Freiberg, WS 2011/12
195
Numerik I
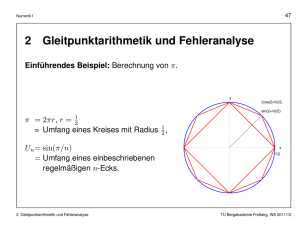
Das (allgemeine) Interpolationsproblem.
Zu gegebener Funktion f : [a, b] → R und gegebenen Stützstellen (Knoten)
a ≤ x0 < x1 < x2 < · · · < xn ≤ b
soll eine einfache“ Funktion p : [a, b] → R konstruiert werden, die die Inter”
polationsbedingungen p(xi ) = f (xi ) (i = 0, 1, . . . , n) erfüllt.
Wozu?
• f ist nur an diskreten Punkten bekannt (Messwerte), aber eine geschlossene Formel für f ist auf ganz [a, b] erwünscht (z.B. um f an
Zwischenstellen x ∈ [a, b] \ {x0 , x1 , . . . , xn } auszuwerten),
• f ist kompliziert“ und soll durch eine einfache“ Funktion angenähert
”
”
0
werden (z.B. um die Ableitung f (x), x ∈ [a, b], oder das Integral
Rb
f (x)dx näherungsweise zu bestimmen).
a
5 Interpolation und numerische Approximation
TU Bergakademie Freiberg, WS 2011/12
196
Numerik I
5.1
Polynominterpolation
Polynomiale Interpolationsaufgabe.
Zu gegebenen (paarweise verschiedenen) Knoten a ≤ x0 < x1 < x2 <
· · · < xn ≤ b und gegebenen Funktionswerten f0 , f1 , . . . , fn ∈ R soll ein
Interpolationspolynom
p(x) = πn xn + πn−1 xn−1 + · · · + π1 x + π0 ∈ Pn
(mit reellen Koeffizienten π0 , π1 , . . . , πn = n + 1 Freiheitsgrade) vom Grad n
konstruiert werden, das die n + 1 Interpolationsbedingungen
p(xi ) = fi
(i = 0, 1, . . . , n)
erfüllt.
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
197
Numerik I
Satz 5.1 Die polynomiale Interpolationsaufgabe ist eindeutig lösbar. Mit
den Lagrange-Grundpolynomen
n
Y
x − xj
`i (x) :=
∈ Pn
x
−
x
i
j
j=0
j6=i
(beachte `i (xi ) = 1 und `i (xj ) = 0 für j 6= i) lässt sich das Interpolationspolynom in der Lagrange-Form
p(x) =
n
X
fi `i (x)
i=0
darstellen.
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
198
Numerik I
Beispiel 1.
Daten:
(x0 , f0 ) = (−1, −1),
(x1 , f1 ) = (0, −1),
(x2 , f2 ) = (2, 2).
3.5
3
P
2.5
2
Lagrange-Grundpolynome:
1.5
L0
L1
L2
1
`0 (x) = x(x − 2)/3,
0.5
`1 (x) = (x + 1)(x − 2)/(−2),
0
`2 (x) = (x + 1)x/6.
−0.5
−1
−1.5
Interpolationspolynom:
−2
−1
0
1
2
3
p(x) = −`0 (x) − `1 (x) + 2`2 (x)
= x2 /2 + x/2 − 1.
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
199
Numerik I
Die Auswertung der Lagrange-Formel ist aufwändig, wenn ein neuer Knoten hinzukommt. Eine rekursive Berechnung ist ökonomischer:
Lemma 5.2 Für eine beliebige Indexmenge 0 ≤ i0 < i1 < · · · < ik ≤ n
bezeichne pi0 ,i1 ,...,ik das (nach Satz5.1 eindeutig bestimmte) Polynom vom
Grad k, das die Bedingungen
pi0 ,i1 ,...,ik (xij ) = fij
(j = 0, 1, . . . , k)
erfüllt.
Dann gilt die Rekursionsformel
pi (x) =
pi0 ,i1 ,...,ik (x) =
5.1 Polynominterpolation
fi ,
(x − xi0 )pi1 ,i2 ,...,ik (x) − (x − xik )pi0 ,i1 ,...,ik−1 (x)
.
x ik − x i0
TU Bergakademie Freiberg, WS 2011/12
200
Numerik I
Rechenschema (Algorithmus von Neville-Aitken):
xi
k=0
x0
p0 (x) = f0
k=1
k=2
k=3
k=4
p0,1 (x)
x1
p1 (x) = f1
p0,1,2 (x)
p1,2 (x)
x2
p2 (x) = f2
p0,1,2,3 (x)
p1,2,3 (x)
p2,3 (x)
x3
p3 (x) = f3
p0,1,2,3,4 (x)
p1,2,3,4 (x)
p2,3,4 (x)
p3,4 (x)
x4
p4 (x) = f4
(Berechnungsreihenfolge : p0 → p1 → p0,1 → p2 → p1,2 → p0,1,2 → · · · )
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
201
Numerik I
Beispiel 2 (vgl. Beispiel 1).
xi
k=0
−1
−1
k=1
k=2
(x−(−1))(−1)−(x−0)(−1)
0−(−1)
0
= −1
−1
(x−0)2−(x−2)(−1)
2−0
2
= 23 x − 1
(x−(−1))(3x/2−1)−(x−2)(−1)
2−(−1)
= 12 x2 + 12 x − 1
2
Aufwand des Neville-Aitken Schemas (für Auswertung des Interpolationspolynoms vom Grad n an einer Stelle x):
5 2
7
2 n + 2 n + 1 Gleitpunktoperationen (falls die Differenzen x − xi (0 ≤ i ≤ n)
vorab bestimmt werden).
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
202
Numerik I
Tableau der dividierten Differenzen von {(xi , fi )}:
xi
k=0
x0
f0
k=1
k=2
k=3
k=4
f0,1
x1
f1
f0,1,2
f1,2
x2
f2
f0,1,2,3
f1,2,3
f2,3
x3
f3
f0,1,2,3,4
f1,2,3,4
f2,3,4
f3,4
x4
f4
mit xi , fi gegeben und
fi0 ,i1 ,...,ik
5.1 Polynominterpolation
fi1 ,i2 ,...,ik − fi0 ,i1 ,...,ik−1
:=
x ik − x i0
(k ≥ 1).
TU Bergakademie Freiberg, WS 2011/12
203
Numerik I
Satz 5.3 Mit Hilfe der dividierten Differenzen läßt sich das (nach Satz 5.1
eindeutig bestimmte) Interpolationspolynom p in Newton-Form
p(x)
= f0 + f0,1 (x − x0 ) + f0,1,2 (x − x0 )(x − x1 ) + · · ·
· · · + f0,1,...,n (x − x0 )(x − x1 ) · · · (x − xn−1 )
darstellen.
Rechenaufwand:
• Zur Bestimmung der Differenzentafel: 32 (n2 + n) Gleitpunktoperationen.
• Zur Auswertung des Newtonschen Interpolationspolynoms mit dem
Horner-Schema: 3n Gleitpunktoperationen (pro Auswertungspunkt).
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
204
Numerik I
Beispiel 3 (vgl. Beispiele 1 und 2).
Dividierte Differenzen:
xi
k=0
−1
−1
k=1
f0,1 =
0
(−1)−(−1)
0−(−1)
= 0
−1
f0,1,2 =
f1,2 =
2
k=2
2−(−1)
2−0
=
3/2−0
2−(−1)
=
1
2
3
2
2
Das bedeutet:
p(x) = (−1) + 0 (x − (−1)) +
5.1 Polynominterpolation
1
1
1
(x − (−1))(x − 0) = x2 + x − 1.
2
2
2
TU Bergakademie Freiberg, WS 2011/12
205
Numerik I
Satz 5.4 (Fehler der Polynominterpolation) Für f ∈ C n+1 [a, b] sei p das
Polynom vom Grad n, welches f an den Knoten a ≤ x0 < x1 < · · · < xn ≤ b
interpoliert. Außerdem bezeichne
wn+1 (x) =
n
Y
(x − xi ) ∈ Pn+1
i=0
das zugehörige Knotenpolynom.
Dann gibt es zu jedem x ∈ [a, b] ein ξ = ξ(x) ∈ (a, b) mit
wn+1 (x) (n+1)
f (x) − p(x) =
f
(ξ).
(n + 1)!
Mit Mn+1 := maxa≤t≤b |f (n+1) (t)| gilt für alle x ∈ [a, b] die Fehlerabschätzung
Mn+1
|f (x) − p(x)| ≤
max |wn+1 (t)|.
(n + 1)! a≤t≤b
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
206
Numerik I
Optimale“ Knoten. Idee (motiviert durch Fehlerabschätzung):
”
Wähle Knoten a ≤ x0 < x1 < · · · < xn ≤ b so, dass
max |wn+1 (t)| = max
a≤t≤b
a≤t≤b
n
Y
|t − xi |
i=0
so klein wie möglich wird.
Lösung: Tschebyscheff-Knoten
2(n − i) + 1
a+b
b−a
(T)
xi =
cos
π +
2
2n + 2
2
mit
max
a≤t≤b
n
Y
i=0
|t −
x(T)
i |
=2
b−a
4
(i = 0, 1, . . . , n)
n
< max
a≤t≤b
n
Y
|t − xi |
i=0
für jede andere Wahl x0 , . . . , xn der Knoten.
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
207
Numerik I
Knotenpolynome mit äquidistanten und Tschebyscheff-Knoten:
0.8
aequidistante Knoten
Tschebyscheff−Knoten
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
5.1 Polynominterpolation
0
1
2
TU Bergakademie Freiberg, WS 2011/12
208
Numerik I
Beispiel 4. Interpoliere
1
f (x) =
1 + x2
(−5 ≤ x ≤ 5)
(Runge-Funktion)
an n + 1 äquidistanten Stützstellen:
n=10
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
0
0
−1
−5
5.1 Polynominterpolation
n=14
8
0
5
−1
−5
0
5
TU Bergakademie Freiberg, WS 2011/12
209
Numerik I
Beispiel 5. Interpoliere
1
f (x) =
1 + x2
(−5 ≤ x ≤ 5)
(Runge-Funktion)
an n + 1 Tschebyscheff-Knoten:
n=10
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
0
0
−1
−5
5.1 Polynominterpolation
n=14
8
0
5
−1
−5
0
5
TU Bergakademie Freiberg, WS 2011/12
210
Numerik I
Fazit.
Durch eine geeignete Knotenwahl (Tschebyscheff-Knoten) lässt sich auch
die Runge-Funktion durch Interpolationspolynome beliebig genau annähern.
Prinzipiell ist eine Approximation durch Interpolationspolynome aber nur
dann ratsam, wenn man mit wenigen Knoten (d.h. mit Polynomen niedrigen Grades) ausreichend gute Ergebnisse erzielen kann. Das ist i.a.
nur bei extrem glatten Funktionen (wie etwa bei der Exponentialfunktion)
gewährleistet. (Die Runge-Funktion ist zwar in ganz R beliebig oft diffe√
renzierbar, besitzt aber Pole in ± −1. Wie gut eine Funktion durch reelle
Interpolationspolynome genähert werden kann, hängt auch von der Lage
ihrer komplexen Singularitäten ab!)
Polynome hohen Grades neigen zu Oszillationen und sind daher zur Approximation oft unbrauchbar.
5.1 Polynominterpolation
TU Bergakademie Freiberg, WS 2011/12
211
Numerik I
5.2
Spline-Interpolation
Splines sind stückweise Polynome“.a
”
Idee: Um die Güte der Approximation zu verbesseren, wird hier nicht der
Polynomgrad erhöht, sondern die Unterteilung des Intervalls verfeinert.
Seien n + 1 Knoten in [a, b] gegeben:
a = x0 < x1 < · · · < xn−1 < xn = b.
Mit T := [x0 , x1 ] ∪ [x1 , x2 ] ∪ · · · ∪ [xn−1 , xn ] bezeichnen wir die zugehörige
Zerlegung des Intervalls [a, b]. Ein Spline vom Grad k bez. T ist eine Funktion s ∈ C k−1 [a, b], die auf jedem Teilintervall von T mit einem Polynom
vom Grad k übereinstimmt:
s [xi−1, xi ] ∈ Pk für i = 1, 2, . . . , n.
a
Eigentlich: Spezielle biegsame Kurvenlineale, die durch Halterungen gezwungen werden,
auf dem Zeichenpapier gegebene Punkte zu verbinden. Werden im Schiffsbau verwendet.
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
212
Numerik I
Satz 5.5 STk , die Menge aller Splines vom Grad k bez. T , ist ein (n + k)dimensionaler Raum.
Runge−Funktion
Knoten
linearer Spline
kubischer Spline
1
0.8
0.6
0.4
0.2
0
−5
5.2 Spline-Interpolation
−4
−3
−2
−1
0
1
2
3
4
5
TU Bergakademie Freiberg, WS 2011/12
213
Numerik I
Einfachster Fall: k = 1. Splines vom Grad 1 oder lineare Splines.
Die zwei charakteristischen Eigenschaften eines linearen Splines s:
1. Auf jedem Teilintervall [xi−1 , xi ] von T ist s linear:
s(x) = αi + βi x
für alle x ∈ [xi−1 , xi ] und i = 1, 2, . . . , n.
2. Auf ganz [a, b] ist s stetig, d.h. für i = 1, 2, . . . , n − 1
lim s(x) = αi + βi xi = αi+1 + βi+1 xi = lim s(x).
x→xi −
x→xi +
Interpolationsaufgabe:
Zu vorgebener Zerlegung T = [x0 , x1 ] ∪ [x1 , x2 ] ∪ · · · ∪ [xn−1 , xn ] von [a, b]
und zu vorgegebenen Werten f0 , f1 , . . . , fn bestimme einen linearen Spline
s ∈ ST1 mit
s(xi ) = fi für alle i = 0, 1, . . . , n.
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
214
Numerik I
Offensichtlich: Diese Aufgabe ist eindeutig lösbar:
fi − fi−1
s(x) = fi−1 +
(x − xi−1 )
xi − xi−1
für x ∈ [xi−1 , xi ].
1.2
linearer Interpolationsspline
1
0.8
0.6
0.4
0.2
0
x0
x1
x2
0.5
0.6
x3
x4
−0.2
−0.4
−0.6
−0.8
5.2 Spline-Interpolation
0
0.1
0.2
0.3
0.4
0.7
0.8
0.9
1
TU Bergakademie Freiberg, WS 2011/12
215
Numerik I
Fehler des linearen Interpolationssplines: (f ∈ C 2 [a, b])
Lokal, d.h. für x ∈ [xi−1 , xi ]:
|f (x) − s(x)| =
1 00
1
|f (ζ)||(x − xi−1 )(x − xi )| ≤ M2,i h2i
2
8
mit M2,i = maxxi−1 ≤ζ≤xi |f 00 (ζ)| und hi = xi − xi−1 .
Global, d.h. für x ∈ [x0 , xn ]:
1
|f (x) − s(x)| ≤ M2 h2max
8
mit M2 = max1≤i≤n M2,i = maxx0 ≤ζ≤xn |f 00 (ζ)| und hmax = max1≤i≤n hi .
Adaptive Knotenwahl. Stategie: Fehler etwa gleich auf jedem Teilintervall.
p
D.h.: Wähle hi invers proportional zu M2,i (viele Knoten dort, wo die
Krümmung von f groß ist).
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
216
Numerik I
Zur Implementierung.
Gegeben: x0 , x1 , . . . , xn und f0 , f1 , . . . , fn .
Gesucht: Wert s(x) des linearen Interpolationssplines an der Stelle x.
Bestimme gi−1 = (fi − fi−1 )/(xi − xi−1 ) für i = 1, 2, . . . , n.
Falls x ∈ [xi−1 , xi ], dann s(x) = fi−1 + gi−1 (x − xi−1 ).
Problem: Gegeben x, in welchem Teilintervall [xi−1 , xi ] liegt x?
Einfach, falls hi = h (äquidistante Knoten):
x − x0
x − x0
i=
:= min k ∈ N : k ≥
.
h
h
Schwieriger bei beliebigen Knoten:
Binäres Suchen ergibt Komplexität von ≈ log2 n.
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
217
Numerik I
Nächster Fall: k = 3:
Gesucht ist ein interpolierender kubischer Spline s ∈ ST3 .
Charakteristische Eigenschaften des kubischen Splines:
1. Auf jedem Teilintervall [xi−1 , xi ] von T ist s kubisch:
s(x) = pi (x) = αi + βi (x − xi−1 ) + γi (x − xi−1 )2 + δi (x − xi−1 )3 .
2. Auf ganz [a, b] ist s zweimal stetig differenzierbar, d.h.:
pi (xi ) = pi+1 (xi ), p0i (xi ) = p0i+1 (xi ), p00i (xi ) = p00i+1 (xi )
für i = 1, 2, . . . , n − 1.
3. Interpolationsbedingungen:
s(xi ) = fi
(i = 0, 1, . . . , n)
(Also 3(n − 1) + (n + 1) = 4n − 2 Bedingungen, aber 4n Freiheitsgrade).
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
218
Numerik I
Drei Möglichkeiten für die erforderlichen zwei Zusatzbedingungen.
Natürlicher Spline:
s00 (x0 ) = s00 (xn ) = 0
(N)
Hermitescher oder vollständiger Spline:
s0 (x0 ) = f00 und s0 (xn ) = fn0 mit f00 , fn0 ∈ R.
(H)
Periodischer Spline: Falls s(x0 ) = s(xn ),
s0 (x0 ) = s0 (xn ) und s00 (x0 ) = s00 (xn ).
5.2 Spline-Interpolation
(P)
TU Bergakademie Freiberg, WS 2011/12
219
Numerik I
Berechnung des kubischen Interpolationssplines.
Auf jedem Teilintervall [xi−1 , xi ] hat der kubische Spline die Form
s(x) = pi (x) = αi + βi (x − xi−1 ) + γi (x − xi−1 )2 + δi (x − xi−1 )3 .
Die Koeffizienten lassen sich durch die
Momente µi := s00 (xi ) und die Funktionswerte fi
(i = 0, 1, . . . , n)
darstellen: (hierbei sei hi := xi − xi−1 )
αi = fi−1 ,
1
γi = µi−1 ,
2
fi − fi−1
hi
βi =
− (µi + 2µi−1 ),
hi
6
µi − µi−1
δi =
.
6hi
M. a. W.: Ein kubischer Spline ist durch die Funktionswerte fi und die
Momente µi (i = 0, 1, . . . , n) eindeutig bestimmt.
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
220
Numerik I
Die (n + 1) Momente µi erfüllen die (n − 1) linearen Gleichungen
hi
hi + hi+1
hi+1
fi+1 − fi
fi − fi−1
µi−1 +
µi +
µi+1 =
−
6
3
6
hi+1
hi
(i = 1, 2, . . . , n − 1) und zwei Zusatzgleichungen:
(N)
µ0 = 0,
µn = 0,
(H)
(P)
h1
f1 − f0
h1
µ0 + µ1 =
− f00 ,
3
6
h1
hn
fn − fn−1
hn
0
µn−1 +
µn = fn −
,
6
3
hn
µ0 − µn = 0,
h1
h1 + hn
f1 − fn
fn − fn−1
h1
µ1 + µn−1 +
µn =
−
.
6
6
3
h1
hn
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
221
Numerik I
Sei
HTk
:= f ∈ C
kf 00 k2 :=
"Z
a
b
k−1
k
[a, b] : f [xi−1 ,xi ] ∈ C [xi−1 , xi ] und
#1/2
|f 00 (x)|2 dx
=
" n Z
X
i=1
#1/2
xi
|f 00 (x)|2 dx
xi−1
(f ∈ HTk , k ≥ 2).
Lemma 5.6 Für f ∈ HT2 und s ∈ ST3 gilt
kf 00 − s00 k22 = kf 00 k22 − ks00 k22
"
b
− 2 (f 0 (x) − s0 (x))s00 (x)|a −
n
X
#
x +
(f (x) − s(x))s000 (x)|xii−1 − .
i=1
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
222
Numerik I
Satz 5.7 [Minimierungseigenschaft kubischer Splines].
Ist f ∈ HT2 und s ∈ ST3 ein zugehöriger kubische Interpolationsspline, der
eine der drei Zusatzbedingungungen (N), (H) oder (P) erfüllt, dann folgt
!
Z
b
ks00 k22
≤
kf 00 k22
f 00 (x)2 dx .
=:
a
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
223
Numerik I
Interpretation von Satz 5.7.
Die Biegeenergie
Z b
Z b
00
2
f (x)
00
2
EB (f ) =
dx
≈
f
(x)
dx
0
2
3/2
a (1 + f (x) )
a
wird näherungsweise durch den kubischen Interpolationsspline s minimiert.
Im folgenden werden nur vollständige kubische Splines (Bedingung (H))
betrachtet, analoge Aussagen gelten unter den Voraussetzungen (N) und
(P).
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
224
Numerik I
Die Momente erfüllen das LGS (s.o.)
h
h
1
3
 h1
6






mit d0 =
fn0 −
f1 −f0
h1

1
6
h1 +h2
3
h2
6
..
..
.
.
hn−1
6
− f00 , dj =
..
.
hn−1 +hn
3
hn
6
fj+1 −fj
hj+1
−
µ0


d0


 

  µ1   d1 

 

  ..   .. 
 .  =  . 

 






hn
µ
d
 n−1 
6   n−1 
hn
3
fj −fj−1
hj
µn
dn
(1 ≤ j ≤ n) und dn =
fn −fn−1
.
hn
Lemma 5.8 Für jede Wahl der Knoten a = x0 < x1 < · · · < xn = b ist
dieses Gleichungssystem eindeutig lösbar. D.h.: Zu jeder Knotenwahl gibt
es genau einen vollständigen kubischen Interpolationsspline für f .
5.2 Spline-Interpolation
TU Bergakademie Freiberg, WS 2011/12
225
Numerik I
Satz 5.9 [Fehler bei kubischer Spline-Interpolation].
Ist f ∈ C 4 [a, b] und s ∈ ST3 der vollständige kubische Interpolationsspline
für f , dann gelten
5
M4 h4max ,
384
x∈[a,b]
1
0
0
max |f (x) − s (x)| ≤
M4 h3max ,
24
x∈[a,b]
3
00
00
max |f (x) − s (x)| ≤ M4 h2max
8
x∈[a,b]
max |f (x) − s(x)|
≤
mit
M4 := max |f (4) (x)|
a≤x≤b
und
hmax = max hi = max (xi − xi−1 ).
1≤i≤n
5.2 Spline-Interpolation
1≤i≤n
TU Bergakademie Freiberg, WS 2011/12
226
Numerik I
5.3
Diskrete Fourier-Transformation
Für n ≥ 0 und reellen Koeffizienten α0 , α1 , . . . , αn sowie β1 , β2 , . . . , βn
bezeichnen wir als trigonometrisches Polynom einen Ausdruck der Form
n
i
α0 Xh
+
αk cos(kx) + βk sin(kx) ,
tn (x) =
2
k=1
wobei βn = 0 für n gerade.
Die trigonometrische Interpolationsaufgabe besteht darin, zu den m äquidistanten Knoten xj = 2πj/m, (j = 0, 1, . . . , m − 1) im Intervall [0, 2π) und m
gegebenen reellen Zahlen f0 , f1 , . . . , fm−1 ein trigonometrisches Polynom
tn zu bestimmen, welches die m Interpolationsbedingungen
tn (xj ) = fj
erfüllt. Hierbei sei n =
5.3 Diskrete Fourier-Transformation
(j = 0, 1, . . . , m − 1)
(
(m − 1)/2 m ungerade
m/2
m gerade.
TU Bergakademie Freiberg, WS 2011/12
227
Numerik I
Transformation auf den (komplexen) Einheitskreis:
φ : [0, 2π) −→ T := {z ∈ C : |z| = 1},
x 7→ z = exp(ix) = cos x + i sin x.
Die Knoten xj gehen in die m-ten Einheitswurzeln über:
j
φ(xj ) = exp(2πij/m) = [exp(2πi/m)]j = ωm
(j = 0, 1, . . . , m − 1)
mit ωm := exp(2πi/m) = cos(2π/m) + i sin(2π/m).
Setzt man β0 = 0 und für k = 0, 1, . . . , n
"
"
#
"
#
1
ak
1 1
2
2 (αk − iβk )
C 3
:= 1
=
2 1
a−k
2 (αk + iβk )
5.3 Diskrete Fourier-Transformation
#" #
−i αk
i
βk
, d.h.
TU Bergakademie Freiberg, WS 2011/12
228
Numerik I
"
R2 3
αk
#
"
=
βk
#"
1
1
i
−i
ak
#
"
=
a−k
ak + a−k
#
i(ak − a−k )
"
=
2 Real (ak )
#
−2 Imag(ak )
,
so folgt
tn (x) =
n
X
ak exp(ikx) =
k=−n
mit p2n (z) =
n
X
ak z k = z −n
k=−n
Pn
k+n
=
k=−n ak z
n
X
ak z k+n = z −n p2n (z)
k=−n
P2n
j=0
aj−n z j ∈ P2n . Wegen
j
jn
jn
p2n (ωm
) = ωm
tn (xj ) = ωm
fj
ist die trigonometrische Interpolationsaufgabe zurückgeführt auf ein (gewöhnliches, wenn auch komplexes) Interpolationsproblem für algebraische Polynome.
5.3 Diskrete Fourier-Transformation
TU Bergakademie Freiberg, WS 2011/12
229
Numerik I
Satz 5.10 Zu beliebig vorgegebenen Funktionswerten f0 , f1 , . . . , f2n ∈ R
gibt es genau ein reelles trigonometrisches Polynom tn ∈ Tn mit
tn (xj ) = fj
(j = 0, 1, . . . , 2n).
k
Lemma 5.11 Für die m-ten Einheitswurzeln ωm
(k ∈ Z, m ∈ N) gelten:
a)
k
kj
j
[ωm
] = ωm
= [ωm
]
j
k
b)
k`
k
ωm`
= ωm
(` ∈ Z, ` 6= 0),
c)
k = ω −k ,
ωm
m
(
m−1
X
m, falls k = 0 (mod m),
kj
ωm =
0, falls k 6= 0 (mod m).
j=0
d)
5.3 Diskrete Fourier-Transformation
(j ∈ Z),
TU Bergakademie Freiberg, WS 2011/12
230
Numerik I
Satz 5.12 Das komplexe (algebraische) Interpolationspolynom pm−1 (z) =
Pm−1
k
j
c
z
∈
P
mit
p
(ω
k
m−1
m−1
m ) = fj ∈ C
k=0
(j = 0, 1, . . . , m − 1) besitzt die Koeffizienten
m−1
1 X
−kj
fj ωm
ck =
m j=0
(k = 0, 1, . . . , m − 1).
In Matrix-Vektor-Schreibweise


c0


 c1 
1


 .  = Fm
 ..  m


cm−1

f0



 f1 


 . 
 .. 


fm−1
mit der Fourier-Matrix
5.3 Diskrete Fourier-Transformation
TU Bergakademie Freiberg, WS 2011/12
231
Numerik I
Fm
−kj := ωm 0≤k,j≤m−1

1

1

= .
 ..

1
1
−1
ωm
···
1
···
−m+1
ωm
..
.
..
.
−m+1
ωm
−(m−1)2
ωm
···




.


Bemerkung. Seien m ∈ N, d ∈ N0 , d ≤ m − 1, f0 , f1 , . . . , fm−1 ∈ C
j
und zj = ωm
(j = 0, 1, . . . , m − 1). Unter allen Polynomen q ∈ Pd vom
Grad d minimiert pm,d (z) = c0 + c1 z + · · · + cd z d , also das “abgeschnittene”
Pm−1
Interpolationspolynom, die Fehlerquadratsumme j=0 |fj − q(zj )|2 :
m−1
X
|fj − pm,d (zj )|2 <
j=0
5.3 Diskrete Fourier-Transformation
m−1
X
|fj − q(zj )|2 für alle q ∈ Pd , q 6= pm,d .
j=0
TU Bergakademie Freiberg, WS 2011/12
232
Numerik I
Satz 5.13 Für m = 2n oder m = 2n+1 gibt es zu beliebigen f0 , f1 , . . . , fm−1 ∈
R ein reelles trigonometrisches Interpolationspolynom
"
#
n
X
1
tn (x) = α0 +
αk cos(kx) + βk sin(kx) ∈ Tn
2
k=1
vom Grad n, das die m Bedingungen
tn (2πj/m) = fj
(j = 0, 1, . . . , m − 1)
erfüllt. Seine Koeffizienten sind durch
!
!
m−1
m−1
2πj
2πj
2 X
2 X
fj cos k
fj sin k
αk =
bzw. βk =
m j=0
m
m j=0
m
(k = 0, 1, . . . , n) gegeben.
Im Fall m = 2n muß βn = 0 gesetzt und αn halbiert werden.
5.3 Diskrete Fourier-Transformation
TU Bergakademie Freiberg, WS 2011/12
233
Numerik I
5.4
Schnelle Fourier-Transformation (FFT)
j
Seien ωm
(j = 0, . . . , m − 1, ωm := exp(2πi/m)) die m-ten Einheitswurzeln.
Diskrete Fourier-Analyse:
Bestimme zu vorgebenen Funktionswerten f0 , . . . , fm−1 ∈ C die KoeffiPm−1
j
zienten c0 , . . . , cm−1 des Interpolationspolynoms P (z) =
j=0 cj z mit
j
P (ωm
) = fj für j = 0, . . . , m − 1.
−kj
Wir wissen: Mit der Fourier-Matrix Fm := [ωm
]0≤k,j≤m−1 ∈ Cm×m gilt




c0
f0




 c1 


1

 f1 

 .  = Fm  .  .
 ..  m
 .. 




cm−1
fm−1
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
234
Numerik I
Diskrete Fourier-Synthese:
Inverse Aufgabe: Bestimme zu vorgebenen Koeffizienten c0 , . . . , cm−1 ∈ C
Pm−1
die Funktionswerte f0 , . . . , fm−1 des Polynoms P (z) = j=0 cj z j an den
0
m−1
m-ten Einheitswurzeln ωm
, . . . ωm
.
Offensichtlich:

f0


c0





 c1 
 f1 




 .  = Wm  . 
 .. 
 .. 




cm−1
fm−1
kj
mit der Matrix Wm := [ωm
]0≤k,j≤m−1 = F̄m ∈ Cm×m .
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
235
Numerik I
−kj
Lemma 5.14 Für die Fourier-Matrix Fm = [ωm
]0≤k,j≤m−1 ∈ Cm×m gelten:
T
H
(a)
Fm
= Fm (aber Fm
6= Fm für m > 2!),
H
(b)
Fm
Fm = mIm , d.h. die Spalten von Fm sind orthogonal
√
und besitzen alle die Euklid-Norm m.
1
1
H
−1
Fm
=m
F̄m .
(c)
Fm
=m
Diskrete Fourier-Transformationen (d.h. diskrete Fourier-Analysen und
Synthesen) müssen in der Praxis oft berechnet werden (Signalverarbeitung, Lösung der Poisson-Gleichung etc.). Die “klassische” Berechnung
einer Fourier-Transformation (ein Matrix-Vektor-Produkt mit Fm /m bzw.
Wm ) erfordert offenbar O(m2 ) komplexe Multiplikationen. Bei Anwendung
der schnellen Fourier-Transformation (FFT) reduziert sich dieser Aufwand
auf O(m log2 m).
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
236
Numerik I
Diese Verbesserung kann nicht überbewertet werden:
“It [the FFT] has changed the face of science and engineering so much
that it is not an exaggeration to say that life as we know it would be very
different without the FFT.”
[Charles Van Loan, Computational Frameworks for the Fast Fourier Transform,
SIAM, Philadelphia 1992, p. ix]
Wir setzen (aus schreibtechnischen Gründen) im folgenden
2πi
2π
2π
ζm = ω̄m = exp −
= cos
− i sin
,
m
m
m
kj
so dass Fm = [ζm
]0≤k,j≤m−1 .
Außerdem sei m gerade.
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
237
Numerik I
Die Idee der FFT (für m = 8): Mit ζ := ζ8 ist

1 1
1
1
1
1

1 ζ ζ 2 ζ 3 ζ 4 ζ 5


1 ζ 2 ζ 4 ζ 6 ζ 8 ζ 10

1 ζ 3 ζ 6 ζ 9 ζ 12 ζ 15

F8 = 
1 ζ 4 ζ 8 ζ 12 ζ 16 ζ 20


1 ζ 5 ζ 10 ζ 15 ζ 20 ζ 25

1 ζ 6 ζ 12 ζ 18 ζ 24 ζ 30

1 ζ 7 ζ 14 ζ 21 ζ 28 ζ 35
5.4 Schnelle Fourier-Transformation (FFT)
1
ζ
6
ζ 12
ζ 18
ζ 24
ζ 30
ζ 36
ζ 42
1


ζ 


ζ 14 

21 
ζ 
.
28 
ζ 

ζ 35 

42 
ζ 
ζ 49
7
TU Bergakademie Freiberg, WS 2011/12
Numerik I
238
Wegen ζ 8 = 1, d.h. ζ j = ζ k , wenn j − k (ohne Rest) durch 8 teilbar ist, folgt


1 1 1 1 1 1 1 1


1 ζ ζ 2 ζ 3 ζ 4 ζ 5 ζ 6 ζ 7 




1 ζ 2 ζ 4 ζ 6 1 ζ 2 ζ 4 ζ 6 


1 ζ 3 ζ 6 ζ ζ 4 ζ 7 ζ 2 ζ 5 


F8 = 
.
4
4
4
4
1 ζ
1 ζ
1 ζ
1 ζ 




1 ζ 5 ζ 2 ζ 7 ζ 4 ζ ζ 6 ζ 3 


1 ζ 6 ζ 4 ζ 2 1 ζ 6 ζ 4 ζ 2 


1 ζ7 ζ6 ζ5 ζ4 ζ3 ζ2 ζ1
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
239
Numerik I
Jetzt numerieren wir die Zeilen von F8 um: zuerst werden
radem (0,2,4,6), danach die mit ungeradem Index (1,3,5,7)
zugehörige Pemutationsmatrix wird mit P bezeichnet.


1 1 1 1 1 1 1 1


 1 ζ2 ζ4 ζ6 1 ζ2 ζ4 ζ6 




 1 ζ4 1 ζ4 1 ζ4 1 ζ4 


"
 1 ζ6 ζ4 ζ2 1 ζ6 ζ4 ζ2 
B1,1


P F8 = 
 =:
 1 ζ ζ2 ζ3 ζ4 ζ5 ζ6 ζ7 
B2,1




 1 ζ3 ζ6 ζ ζ4 ζ7 ζ2 ζ5 


 1 ζ5 ζ2 ζ7 ζ4 ζ ζ6 ζ3 


1 ζ7 ζ6 ζ5 ζ4 ζ3 ζ2 ζ1
5.4 Schnelle Fourier-Transformation (FFT)
die mit gegezählt. Die
B1,2
#
B2,2
TU Bergakademie Freiberg, WS 2011/12
240
Numerik I
Wir untersuchen die einzelnen Blöcke: Wegen ζ = ζ8 ist ζ 2 = ζ4 , d.h.


1 1 1 1


1 ζ4 ζ42 ζ43 

B1,1 = B1,2 = 
1 ζ 2 ζ 4 ζ 6  = F4 .

4
4
4
1 ζ43 ζ46 ζ49
Aus den Spalten 0,1,2
“aus”:

1

1
B2,1 = 
1

1
5.4 Schnelle Fourier-Transformation (FFT)
bzw. 3 von B2,1 “klammern” wir ζ 0 , ζ 1 , ζ 2 bzw. ζ 3
1
1
ζ2
ζ4
ζ4
1
ζ6
ζ4

1
1


ζ 6
 0

ζ 4
 0
ζ2
0

0
0
0
ζ
0
0
ζ2
0
0

0
 = F4 D 4 .
0

ζ3
TU Bergakademie Freiberg, WS 2011/12
241
Numerik I
Analog:
B2,2

1

1
=
1

1
1
1
ζ2
ζ4
ζ4
1
ζ6
ζ4

1
ζ4


ζ 6
 0

ζ 4
 0
ζ2
0
Insgesamt erhalten wir
"
F4
P F8 =
F4 D4
5.4 Schnelle Fourier-Transformation (FFT)
F4
−F4 D4

0
0
0
ζ5
0
0
ζ6
0
0

0
 = F4 (ζ 4 D4 ) = −F4 D4 .
0

ζ7
#
"
=
F4
O
O
F4
#"
I4
I4
D4
−D4
#
.
TU Bergakademie Freiberg, WS 2011/12
242
Numerik I
Satz 5.15 Seien m gerade, σ die folgende (even/odd) Permutation
σ = [0, 2 . . . , m − 2, 1, 3, . . . , m − 1]
und P = Pσ die zugehörige Permutationsmatrix.
Dann besitzt die zeilenpermutierte Fourier-Matrix Fm die Zerlegung
"
# "
#"
#
Fm/2
Fm/2
Fm/2
O
Im/2
Im/2
P Fm =
=
.
Fm/2 Dm/2 −Fm/2 Dm/2
O
Fm/2 Dm/2 −Dm/2
Dabei bezeichnet Dm/2 die Diagonalmatrix
0
1
m/2−1
∈ C(m/2)×(m/2)
Dm/2 = diag ζm
, ζm
, . . . , ζm
mit ζm = ω̄m = exp(−2πi/m).
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
243
Numerik I
Berechne jetzt y = Fm x für ein x ∈ Cm (m gerade).
Wegen der Zerlegung von Fm aus Satz 17 unterteilen wir dies in zwei
Schritte:
1. Reduktionsschritt: Berechne
"
#
Im/2
Im/2
z =
x.
Dm/2 −Dm/2
Für m = 8:
z0 = x0 + x4 ,
z1 = x1 + x5 ,
z2 = x2 + x6 ,
z3 = x3 + x7
z4 = (x0 − x4 ),
z5 = (x1 − x5 )ζm ,
2
3
z6 = (x2 − x6 )ζm
, z7 = (x3 − x7 )ζm
(m/2 komplexe Multiplikationen und m komplexe Additionen).
2. Berechne
Fm/2 z (0 : m/2 − 1)
und
Fm/2 z (m/2 : m − 1)
(zwei Fourier-Transformationen der Dimension m/2).
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
244
Numerik I
Ist m = 2p eine Potenz von 2, so ist m/2 ebenfalls gerade und die beiden
Fourier-Transformationen der Dimension m/2 können auf vier FourierTransformationen der Dimension m/4 reduziert werden. Der Aufwand zur
Reduktion beträgt 2·m/4 = m/2 komplexe Multiplikationen (und 2·m/2 = m
komplexe Additionen). Diese Prozess wird solange fortgesetzt bis man
eine Multiplikation mit Fm auf m Multiplikationen mit F1 = [1] reduziert
hat (eine Multiplikation mit F1 erfordert offenbar keinen Aufwand). Dieses
Reduktionsverfahren heißt schnelle Fourier-Transformation (FFT = Fast
Fourier Transformation).
Satz 5.16 Zur Durchführung einer schnellen Fourier-Transformation der
Ordnung m = 2p sind
m
m
p=
log2 (m)
2
2
komplexe Multiplikationen
und m log2 (m) komplexe Additionen erforderlich.
5.4 Schnelle Fourier-Transformation (FFT)
TU Bergakademie Freiberg, WS 2011/12
245
Numerik I
Die konventionelle Berechnung einer Fourier-Transformation der Länge
m = 2p durch Fm x erfordert also 2p+1 /p-mal mehr Multiplikationen als
ihre Berechnung durch FFT. Wenn z.B. für p = 20 die FFT-Version eine
Sekunde benötigt, so benötigt Fm x etwa 29 Stunden.
Verbleibendes Problem: Bestimmt man y = Fm x durch FFT, so erhält man
e = Qy mit einer Permutatinicht y , sondern einen permutierte Version y
onsmatrix Q ∈ Rm×m .
Es gilt: Besitzt für m = 2p der Index i ∈ {0, 1, . . . , m−1} die Binärdarstellung
i = bp−1 2p−1 + · · · + b2 22 + b1 2 + b0 =: [bp−1 . . . b2 b1 b0 ]2 , und ist
r(i) := [b0 b1 b2 . . . bp−1 ]2 = b0 2p−1 + b1 2p−2 + b2 2p−3 + · · · + bp−1
(bit reversal), dann gelten
yi = yer(i)
5.4 Schnelle Fourier-Transformation (FFT)
und
yei = yr(i) .
TU Bergakademie Freiberg, WS 2011/12
246
Numerik I
5.5
Eine Anwendung
Interpretiere die m Ecken eines Polygons, (x0 , y0 ), . . . , (xm−1 , ym−1 ), als
komplexe Zahlen: f0 = x0 + iy0 , . . . , fm−1 = xm−1 + iym−1 (i2 = −1).
Das Ergebnis einer diskreten Fourier-Analyse dieser Zahlen
1
[c0 , c1 , . . . , cm−1 ] = Fm [f0 , f1 , . . . , fm−1 ]>
m
>
nennt man diskretes komplexes Spektrum des Polygons. Es spiegelt
geometrische Eigenschaften des Polygons wider und kann daher zur Klassifikation von Formen (Mustererkennung) verwendet werden.
Lage- und größeunabhängig ist das normierte Amplitudenspektrum
ak = |ck+2 /c1 |
5.5 Eine Anwendung
(k = 0, . . . , m − 3).
TU Bergakademie Freiberg, WS 2011/12
247
Numerik I
5
5
5
4
4
4
3
3
3
2
2
2
1
1
1
0
0
1
2
3
4
5
0
0
1
2
3
4
5
0
0.5
0.5
0.5
0.4
0.4
0.4
0.3
0.3
0.3
0.2
0.2
0.2
0.1
0.1
0.1
0
10
20
30
0
10
20
30
0
0
1
2
10
3
20
4
5
30
a1 < a2 , a2 > a3 ; a1 > a2 , a2 > a3 ; a1 > a2 , a2 < a3 ;
5.5 Eine Anwendung
TU Bergakademie Freiberg, WS 2011/12
248
Numerik I
5
0.5
4.5
0.45
4
Polygon
E
F
H
0.4
3.5
0.35
3
0.3
2.5
0.25
2
0.2
1.5
0.15
1
0.1
0.5
0.05
0
0
5.5 Eine Anwendung
1
2
3
0
0
5
10
15
20
25
30
TU Bergakademie Freiberg, WS 2011/12
249
Numerik I
5
0.5
4.5
Polygon
E
F
H
0.45
4
0.4
3.5
0.35
3
0.3
2.5
0.25
2
0.2
1.5
0.15
1
0.1
0.5
0.05
0
0
5.5 Eine Anwendung
1
2
3
0
0
5
10
15
20
25
30
TU Bergakademie Freiberg, WS 2011/12
250
Numerik I
5
0.5
4.5
0.45
4
0.4
3.5
Polygon
E
F
H
0.35
3
0.3
2.5
0.25
2
0.2
1.5
0.15
1
0.1
0.5
0.05
0
0
5.5 Eine Anwendung
1
2
3
0
0
5
10
15
20
25
30
TU Bergakademie Freiberg, WS 2011/12