Vorlesungsmitschrieb

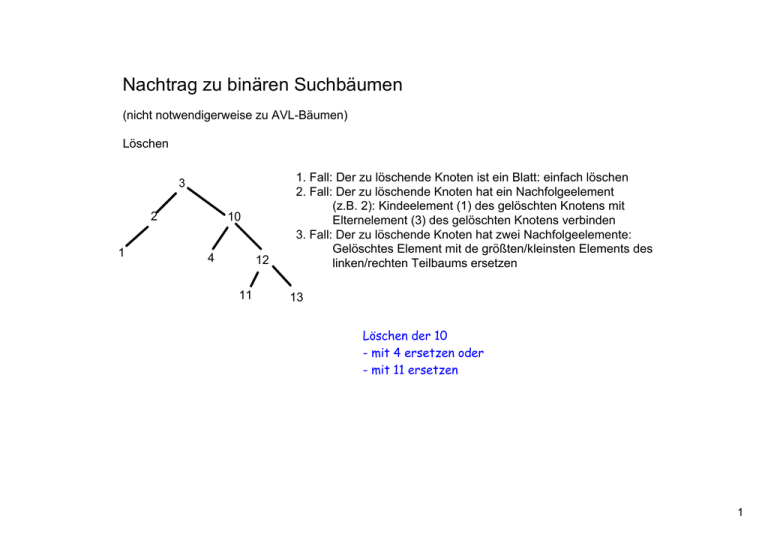
Nachtrag zu binären Suchbäumen
(nicht notwendigerweise zu AVL­Bäumen)
Löschen
3
2
1
10
4
12
11
1. Fall: Der zu löschende Knoten ist ein Blatt: einfach löschen
2. Fall: Der zu löschende Knoten hat ein Nachfolgeelement (z.B. 2): Kindeelement (1) des gelöschten Knotens mit Elternelement (3) des gelöschten Knotens verbinden
3. Fall: Der zu löschende Knoten hat zwei Nachfolgeelemente:
Gelöschtes Element mit de größten/kleinsten Elements des linken/rechten Teilbaums ersetzen
13
Löschen der 10
- mit 4 ersetzen oder
- mit 11 ersetzen
1
B­Bäume
B steht NICHT für binär, sondern für den "Erfinder" Rudolph Bayer
Charakteristiken für einen Baum der Ordnung k
­ Jeder Knoten (außer Wurzel) hat zwischen k und 2k Elemente
­ Jeder Knoten (außer Wurzel) hat i+1 Nachfolgeknoten, wobei i die Anzahl der Elemente des Knotens ist.
­ Alle Wege von der Wurzel zu den Blättern sind gleich lang
­ B­Bäume sind sortiert
­ innerhalb der Knoten
­ Elemente des linken/rechten Teilbaums sind immer kleiner/größer als das Element im Elternkonten
2
Zusammenspiel von Datenbanken und B­Bäumen
Die Knoten/Blätter nennt man bei Datenbanken oft "Pages" (Seiten. Dabei entsprechen die Seiten Speicherheiten auf einem Medium, z.B. auf einer Festplatte.
Der Zugriff auf diese Speichereinheiten (Medium) ist im Vergleich zum Zugriff auf den Hauptspeicher sehr aufwendig/langsam (>Faktor 1000).
Bei Datenbanken wird der Index als Baumstruktur im Hauptspeicher gehalten, so dass man die Seite schnell zum Einfügen, Löschen oder Suchen findet. Erst wenn man die Seite gefundet hat, erfolgt der aufwendige Zugriff auf den Inhalt der Seite.
Wenn man k und damit die Page­Size erhöht
­ wird der Baum (Indexstruktur ­ in rot) und damit der Hauptspeicherbedarf niedriger.
­ wird die Größe der Speichereinheiten (in grün) größer und damit die Zugriffszeit auf deren Inhalt
3
k=1, Einfügen: 1, 5, 2, 6, 7, 8, 3, 4
Regeln zum Einfügen in B­Bäume
Einfügen 3, 2, 5
1. Position für neues Element suchen und dann dort einfügen
2. Prüfen, ob der Knoten danach maximal 2k Elemente hat
a) falls ja: subba, fertig.
b) falls nein: Überlaufbehandlung
Überlaufbehandlung
­ Mittleres Element (hier 3) wandert nach oben (kann rekursiv erfolgen)
­ Es erfolgt ein Split
­ Element links des verschobenen Elements (2) bleibt auf dem Blatt
­ Element rechts des verschobenen Elements (5) wander auf neues Blatt
2
3
5
3
2
5
Überlaufbehandlung
­ Mittleres Element (hier 9) wandert nach oben (kann rekursiv erfolgen)
­ Es erfolgt ein Split
­ Element links des verschobenen Elements (8) bleibt auf dem Blatt
­ Element rechts des verschobenen Elements (11) wander auf neues Blatt
4
k=1, Einfügen: 1, 5, 2, 6, 7, 8, 3, 4
Überlaufbehandlung
­ Mittleres Element (hier 9) wandert nach oben (kann rekursiv erfolgen)
­ Es erfolgt ein Split
­ Element links des verschobenen Elements (8) bleibt auf dem Blatt
­ Element rechts des verschobenen Elements (11) wander auf neues Blatt
2
1 2 5
2
6 7
6
4
4
1
5
1
3
5
7
8
2
1
6
3
5
7
8
5
Regeln zum Löschen in B­Bäumen
Folgende Fälle
­ Element ist im Blatt: Element löschen und ggf. Unterlaufbehandlung
­ Element in sonstigem Knoten: Element löschen und durch das nächst kleinere ersetzen, ggf. Unterlaufbehandlung
keine Unterlaufbehandlung,
da k Elemente verbleiben
(k=2)
6
Unterlaufbehandlung
Fall a) Es verbleiben nicht genügend Elemente, aber beide Seiten inklusive des Elternelements (20) haben genügend Elemente für eine Reorganisation:
Elemente beider Nachbarbarblätter und des Elternelements werden so umorganisiert, dass das mittlere Element (17 oder 18) das neue Elternelement wird.
13, 14, 17, 18, 20, 24
7
Fall b) es verbleiben nicht genügend Elemente und es kann daher nicht mit den Elementen des Nachbarblatts (13, 14) und des Elternelements (20) ausgeglichen werden:
Die beiden benachbarten Seiten/Blätter und das eingeschlossene Elternelement (20) werden zu einer Seite zusammengelegt. Dabei wird das Elternelement heruntergezogen.
Das kann eine weiter Unterlaufbehandlung nach sich ziehen (rekursiv)
8