PDF

http://www.mpi-sb.mpg.de/~sschmitt/info5-ss01
IS
UN
R
Lösungsvorschläge für das 8. Übungsblatt
Letzte Änderung am 27. Juni 2001
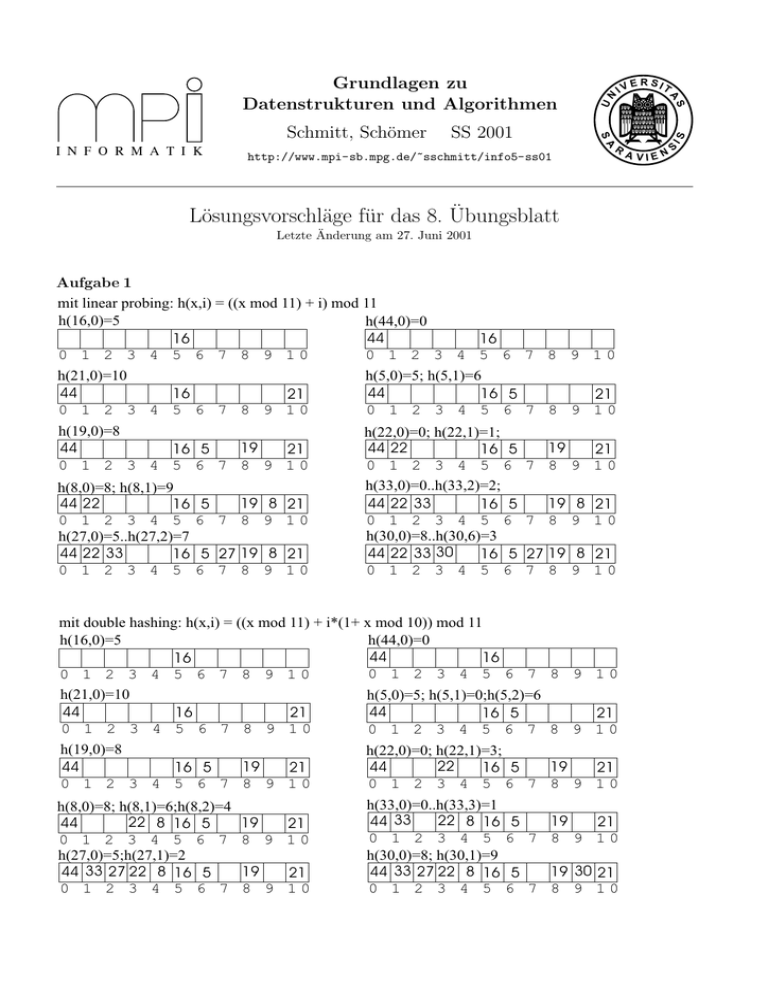
Aufgabe 1
mit linear probing: h(x,i) = ((x mod 11) + i) mod 11
h(16,0)=5
h(44,0)=0
44
16
16
0 1 2 3 4 5 6
0 1 2 3 4 5 6 7 8 9 10
h(21,0)=10
h(5,0)=5; h(5,1)=6
44
44
16
16 5
21
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6
h(19,0)=8
h(22,0)=0; h(22,1)=1;
44
19
44 22
16 5
16 5
21
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6
h(33,0)=0..h(33,2)=2;
h(8,0)=8; h(8,1)=9
44 22
19 8 21
44 22 33
16 5
16 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6
h(30,0)=8..h(30,6)=3
h(27,0)=5..h(27,2)=7
44 22 33
44 22 33 30
16 5 27 19 8 21
16 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6
7 8 9 10
21
7 8 9 10
19
21
7 8 9 10
19 8 21
7 8 9 10
27 19 8 21
7 8 9 10
mit double hashing: h(x,i) = ((x mod 11) + i*(1+ x mod 10)) mod 11
h(16,0)=5
h(44,0)=0
44
16
16
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7 8 9 10
h(21,0)=10
h(5,0)=5; h(5,1)=0;h(5,2)=6
44
44
16
21
16 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7
h(19,0)=8
h(22,0)=0; h(22,1)=3;
22
44
19
44
16 5
16 5
21
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7
h(8,0)=8; h(8,1)=6;h(8,2)=4
22 8 16 5
44
0 1 2 3 4 5 6 7
h(27,0)=5;h(27,1)=2
44 33 27 22 8 16 5
0 1 2 3 4 5 6 7
19
21
8 9 10
19
21
8 9 10
h(33,0)=0..h(33,3)=1
22 8 16
44 33
0 1 2 3 4 5
h(30,0)=8; h(30,1)=9
44 33 27 22 8 16
0 1 2 3 4 5
8 9 10
21
8 9 10
19
21
8 9 10
19
5
21
6 7 8 9 10
19 30 21
5
6 7 8 9 10
S
SS 2001
E R SIT
S
Schmitt, Schömer
SA
IV
A
Grundlagen zu
Datenstrukturen und Algorithmen
A VIE N
Aufgabe 2
1. Da 15 keine Primzahl ist, ist der Restklassenring Z/15Z nicht nullteilerfrei. Ziel des “probing” ist, dass nacheinander Plätze der Hashtabelle ausprobiert werden. Ist c ein Teiler von
m, so werden nicht alle Plätze adressiert. Deshalb sind alle Zahlen c ungeeignet, die nicht
teilerfremd zu 15 sind. Dies sind 3, 5, 6, 9, 10, 12. Sei z.B. c = 3. Dann ist h(x, 0) = h(x, 5).
2. Wie in Aufgabe eins schon bemerkt, müssen m und c teilerfremd sein, d.h. ggT (c, m) = 1.
Es gilt:
∃0 < d < m : d | c ∧ d | m ⇒ ∃1 ≤ k, l ≤ m : c = d · k ∧ m = d · l
⇒ h(x, l) = (h(x) + c · l) mod m = (h(x) + d · k · l) mod m
= (h(x) + d · m) mod m = h(x) mod m = h(x, 0)
Damit alle Plätze der Hashtabelle adressiert werden, muss l = m gelten. Daraus folgt d = 1.
Also sind diejenigen Paare (c, m) sinnvoll mit ggT (c, m) = 1.
Aufgabe 3
a) Die Zahl 257 ist eine Primzahl, daher können wir die 1-universelle Klasse der Hashfunktionen
aus der Vorlesung verwenden. Ein String der Länge l ist dabei ein l-Tupel von Zahlen
s = (sl−1 , . . . , s0 ) und kann als eine Zahl in der Darstellung zur Basis m = 257 betrachtet
werden. Die Hashfunktionen sind dann gegeben durch
ha (s) = a × s
für beliebige Strings a der Länge l, wie in der Vorlesung.
b) Wir wählen jetzt Strings a beliebiger Länge und betrachten auch die Funktionen ha (s) =
a × s wie eben. Seien x, y Strings der Länge lx , ly und l = max{lx , ly }. Dann sind von a nur
die ersten l Stellen wichtig, die hinteren Stellen sind unwichtig. Genau wie in dem Beispiel
der Vorlesung kann man dann zeigen, daß diese Klasse von Funktionen 1-universell ist.
Wie wählt man zufällig einen String a unendlicher Länge? Man wählt sich zufällig Zahlen
aus {0, 1, . . . , 256} für jede Stelle, aber nur soviel, wie man gerade braucht. Hat man z.B.
einen String der Länge 19 zu hashen, wählt man sich die ersten 19 Stellen von a. Hasht man
danach einen String der Länge 99, so läßt man die ersten 19 Stellen von a wie vorher und
wählt sich zufällig die letzten 80 Stellen.
Aufgabe 4
(a) Ein Binärbaum ist so aufgebaut, daß das linke Kind eines jeden Knotens kleiner ist als der
Knoten selbst. Somit ist das Minimum des Teilbaums mit Wurzel v gleichzeitig auch das
Minimum des Teilbaums mit Wurzel v →left, sofern er nicht NULL ist. Besitzt v kein linkes
Kind, so existiert kein kleineres Element im Teilbaum, und v ist selbst das Minimum. Diese
induktive Definition führt uns zur folgenden Implementierung:
// ermittelt das Minimum des Teilbaums mit Wurzel v
handle minimum( handle v)
{
if( NULL == v->left) return v;
return( minimum( v->left));
}
Es stellt sich also heraus, daß das Minimum gerade das linkeste Kind ist, und analog dazu
ist das Maximun das rechteste, was zu dieser Implementierung führt:
// ermittelt das Maximum des Teilbaums mit Wurzel v
handle maximum( handle v)
{
if( NULL == v->right) return v;
return( maximum( v->right));
}
Beide Implementierungen haben logarithmische Laufzeit.
(b) Zeige: Es gibt nur diese 2 Fälle:
(i) v besitzt ein rechtes Kind. Zeige: succ(v) = minimum(v->right)
∗ Alle Elemente im linken Teilbaum von v (falls ein solcher existiert) sind kleiner als
v, kommen also nicht in Frage.
∗ Ist v ein rechtes Kind von v->parent, dann sind alle Elemente im linken Teilbaum
von v->parent sowie v->parent selbst kleiner als v.
∗ Geht man solange nach oben, wie man das rechte Kind eines Elternknotens ist, so
sind diese Elternknoten und ihre linken Teilbäume (genau wie oben) alle kleiner
als v.
∗ Irgendwann auf dem Weg nach oben sind wir das linke Kind eines Knotens w.
Dieser Knoten ist dann größer als v, aber auch größer als minimum(v->right), da
der rechte Unterbaum von v auch links unterhalb w steht.
∗ Ebenso ist alles, was rechts von w steht, größer als minimum(v->right).
∗ Man kann jetzt weiter bis zur Wurzel gehen und wie eben argumentieren: Ist man
das rechte Kind, dann trifft man nur auf Elemente, die kleiner als v sind, ist man
das linke Kind, so trifft man nur auf Elemente, die größer als minimum(v->right)
sind.
(ii) v besitzt kein rechtes Kind. Man geht solange nach oben, wie man das rechte Kind
eines Knotens ist. Ist man das linke Kind eines Knotens w, so ist dieser gleich succ(v).
∗ Auf dem Weg nach oben, bevor man bei w ankommt, sind alle Knoten die man
trifft und ihre linken Teilbäume kleiner als v.
∗ Der Knoten w ist größer als v.
∗ Alle Knoten im rechten Teilbaum von w (falls der existiert) sind größer als w.
∗ Jetzt gehen wir wie in Teil (i) von w aus nach oben. Ist der betrachtete Knoten ein
rechtes Kind des Elternknotens p, dann ist p und der linke Teilbaum von p kleiner
als v (da v im rechten Teilbaum von p liegt).
∗ Ist der betrachtete Knoten ein linkes Kind von p, dann ist p und der rechte Teilbaum von p größer als w.
∗ Genau wie eben kann man mit dieser Argumentation bis zur Wurzel gehen.
(c) Dies sollte uns nun keine Schwierigkeiten mehr bereiten:
// findet das nächst kleinere Element
handle pred( handle v)
{
if( v->left!=0) return maximum( v->left);
handle p = v->parent;
while( p!=0 && v==p->left)
{
v = p;
p = v->parent;
}
return(p);
}
Die Methode hat die gleiche Laufzeit wie succ.