Ubungen zur Physik 2 – Blatt 9

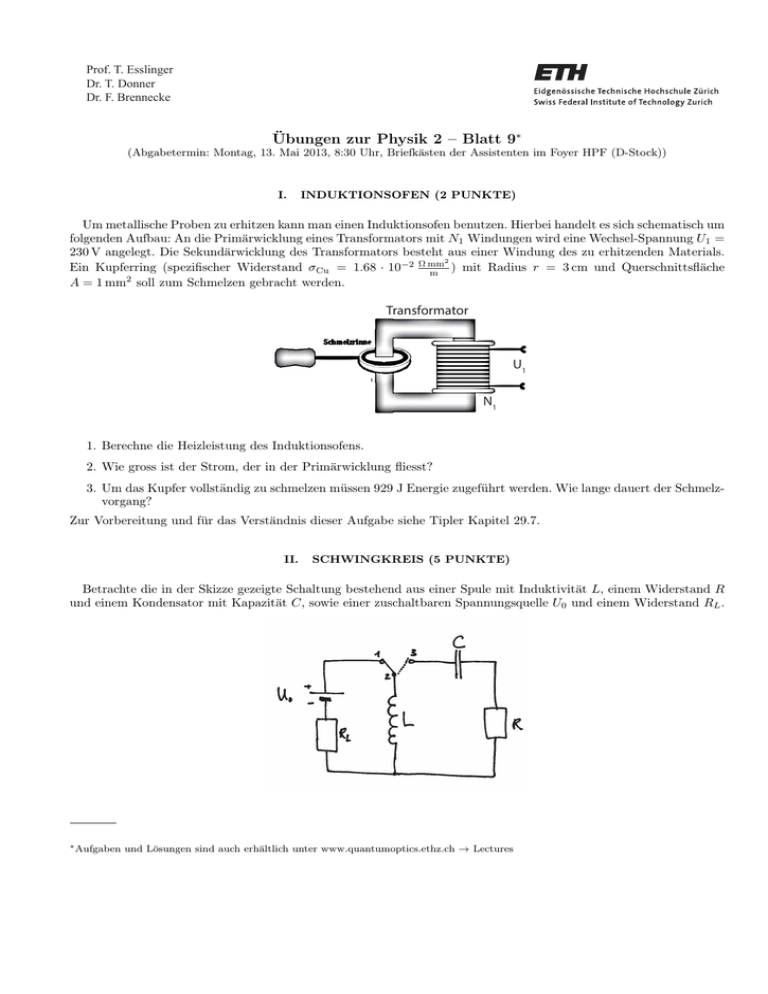
Prof. T. Esslinger
Dr. T. Donner
Dr. F. Brennecke
Übungen zur Physik 2 – Blatt 9∗
(Abgabetermin: Montag, 13. Mai 2013, 8:30 Uhr, Briefkästen der Assistenten im Foyer HPF (D-Stock))
I.
INDUKTIONSOFEN (2 PUNKTE)
Um metallische Proben zu erhitzen kann man einen Induktionsofen benutzen. Hierbei handelt es sich schematisch um
folgenden Aufbau: An die Primärwicklung eines Transformators mit N1 Windungen wird eine Wechsel-Spannung U1 =
230 V angelegt. Die Sekundärwicklung des Transformators besteht aus einer Windung des zu erhitzenden Materials.
2
Ein Kupferring (spezifischer Widerstand σCu = 1.68 · 10−2 Ω mm
m ) mit Radius r = 3 cm und Querschnittsfläche
A = 1 mm2 soll zum Schmelzen gebracht werden.
Transformator
U1
N1
1. Berechne die Heizleistung des Induktionsofens.
2. Wie gross ist der Strom, der in der Primärwicklung fliesst?
3. Um das Kupfer vollständig zu schmelzen müssen 929 J Energie zugeführt werden. Wie lange dauert der Schmelzvorgang?
Zur Vorbereitung und für das Verständnis dieser Aufgabe siehe Tipler Kapitel 29.7.
II.
SCHWINGKREIS (5 PUNKTE)
Betrachte die in der Skizze gezeigte Schaltung bestehend aus einer Spule mit Induktivität L, einem Widerstand R
und einem Kondensator mit Kapazität C, sowie einer zuschaltbaren Spannungsquelle U0 und einem Widerstand RL .
∗ Aufgaben
und Lösungen sind auch erhältlich unter www.quantumoptics.ethz.ch → Lectures
2
1. Der Schalter ist zunächst in der Position 1 − 2, sodass die Spannungsquelle einen Strom I0 durch Spule L und
den Widerstand RL treibt. Berechne diesen Strom und zeichne die Stromrichtung ein.
2. Wird der Kondensator bei dieser Schalterstellung geladen (mit Begründung)?
3. Stelle mit Hilfe der Kirchhoff’schen Maschenregel eine Differentialgleichung für die Ladung Q auf dem Kondensator auf, wenn der Schalter in der Position 2 − 3 ist. Beachte dabei, dass bei der Anwendung der Maschenregel
Spannungen von Elementen bei denen das elektrische Potential im Umlaufsinn abnimmt, ein negatives Vorzeichen erhalten.
4. Mache Dir die weitgehende Analogie zum gedämpftem harmonischen Oszillator aus der Mechanik klar und
identifiziere die einander entsprechenden Grössen.
5. Sei nun der Schalter in der Position 1 − 2. Zum Zeitpunkt t = 0 wird der Schalter in die Position 2 − 3 gebracht.
Wir wollen das Zeitverhalten des Schaltkreises untersuchen. Betrachte zunächst den Fall R = 0.
(a) Berechne und skizziere den zeitlichen Verlauf des Stromes I(t) durch die Spule sowie der Spannung U (t) am
Kondensator. Verwende für die Startbedingung dabei Deine Antwort aus Punkt 2, und drücke die Ladung
Q0 durch die in der Zeichnung gegebenen Grössen aus.
(b) Stelle eine Gleichung für die Gesamtenergie im Schaltkreis auf. Ist die Gesamtenergie zeitlich konstant?
6. Diskutiere nun kurz (ohne Rechnung) den Fall R > 0, wiederum beginnend mit dem Schalten auf Position
1 − 3 bei t = 0. Wie verändert sich qualitativ das Verhalten von Strom und Spannung? Was passiert mit der
elektromagnetischen Gesamtenergie?
Zur Vorbereitung und für das Verständnis dieser Aufgabe siehe Tipler Kapitel 29.5, sowie Kapitel 14.
III.
FARADAY-WAAGE (3 PUNKTE)
Die magnetische Suszeptibilität von para- und diamagnetischen Stoffen lässt sich mit der Faraday-Waage messen:
Die zu untersuchende Probe mit der unbekannten magnetischen Suzeptibilität χm und dem Volumen V wird in
die Nähe eines in z−Richtung verlaufenden Leiters gebracht, der den Strom I führt (der Strom fließt in positive
z−Richtung, also aus dem Blatt heraus). Die Probe ist verbunden mit einer Feder mit der Federkonstante k (deren
anderes Ende fest montiert ist) und mit einem Zeiger, der die Auslenkung der Feder misst.
V
Leiter
y
x
R
~ ·BdV
~
~ ·B
~ der Probe im Magnetfeld des
1. Finde einen Ausdruck für die potentielle Energie Epot = − 21 M
' − 21 V M
geraden Leiters als Funktion der magnetischen Suszeptibilität. Hierbei wird angenommen, dass das Magnetfeld
über die Probe konstant ist. Weiterhin kann angenommen werden, dass die Probe genau senkrecht über dem
Draht hängt, also eindimensional entlang der y-Richtung gerechnet werden kann.
2. Da das Magnetfeld ortsabhängig ist, wirkt eine Kraft auf die Probe. Berechne die Kraft in y-Richtung, wiederum
für den Fall dass die Probe senkrecht über dem Draht hängt.
3. Die Federkonstante beträgt k = 10−6 N/m und in der Ruheposition (I = 0) ist der Abstand der Probe zum Leiter
r = 0.5 cm. Der Strom wird auf 200 A erhöht. Eine Probe aus Aluminium wird um δ =0.234 mm zum Draht
hingezogen und eine Probe aus Kupfer wird um δ = 100 µm weggedrückt. Beide Proben haben ein Volumen
von V = 1 mm3 . Berechne die Suszeptibilitäten von Aluminium und Kupfer.