Computergestütztes wissenschaftliches Rechnen SoSe 2004
Werbung
Computergestütztes wissenschaftliches Rechnen
SoSe 2004
Alexander K. Hartmann, Universität Göttingen
9. Juli 2004
9.2
Finite-size Scaling
Physikalische Systeme: groß (O(1023 ) Teilchen).
Simulationen: endliche (kleine) Systemgrößen.
Ausweg: Studiere mehrere verschiedene Systemgrößen.
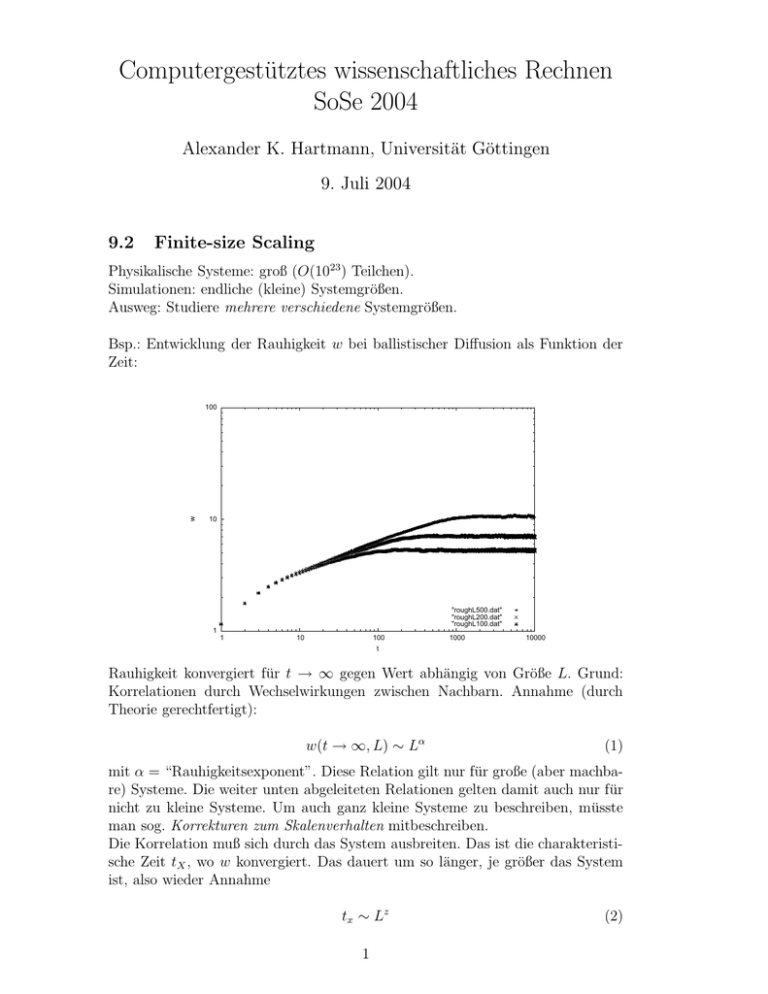
Bsp.: Entwicklung der Rauhigkeit w bei ballistischer Diffusion als Funktion der
Zeit:
w
100
10
"roughL500.dat"
"roughL200.dat"
"roughL100.dat"
1
1
10
100
t
1000
10000
Rauhigkeit konvergiert für t → ∞ gegen Wert abhängig von Größe L. Grund:
Korrelationen durch Wechselwirkungen zwischen Nachbarn. Annahme (durch
Theorie gerechtfertigt):
w(t → ∞, L) ∼ Lα
(1)
mit α = “Rauhigkeitsexponent”. Diese Relation gilt nur für große (aber machbare) Systeme. Die weiter unten abgeleiteten Relationen gelten damit auch nur für
nicht zu kleine Systeme. Um auch ganz kleine Systeme zu beschreiben, müsste
man sog. Korrekturen zum Skalenverhalten mitbeschreiben.
Die Korrelation muß sich durch das System ausbreiten. Das ist die charakteristische Zeit tX , wo w konvergiert. Das dauert um so länger, je größer das System
ist, also wieder Annahme
tx ∼ L z
1
(2)
z = “dynamischer Exponent”. tX beschreibt die typische Zeitskala des Systems.
D.h. das Verhalten des Systems hängt nur von t/tX ab.
Gleichungen (1) und (2) lassen sich durch eine Formel ausdrücken:
w(t, L) = Lα F (t/Lz ) ,
(3)
wobei für die Funktion F (t̃) gelten muß: limt̃→∞ F (t̃) = const.
Von früher wissen wir, dass für kleine Zeiten gilt:
w(t) ∼ tβ
(4)
Also F (t̃) ∼ t̃β für kleine Zeiten t̃ 1, damit
w(t, L) ∼ Lα (t/Lz )β = tβ Lα−zβ
Für kleine Zeiten kann das Verhalten nicht von der Systemgröße abhängen (da
sich die Korrelation noch nicht durch das System “fortgepflanzt” haben kann) →
α − zβ = 0 oder
z = α/β
Das ist eine sogenannte Skalenrelation, weil es eine Verbindung zwischen den verschiedenen Skalenexponenten α, β, z herstellt.
Gl. (3) kann man nutzen um α und z zu bestimmen: Wenn man L−α w(t, L) für
verschiedene Größen L als Funktion von t/Lz plottet, dann müssen alle Datenpunkte auf der gleichen Kurve (gegeben durch die Funktion F (t̃)) liegen. Das
kann man mit gnuplot machen:
gnuplot> z=1.45
gnuplot> a=0.44
gnuplot> plot "roughL100.dat" u ($1/100**z):($2/100**a),
"roughL200.dat" u ($1/200**z):($2/200**a),
"roughL500.dat" u ($1/500**z):($2/500**a)
(Hinweis: noch einfacher ist es, wenn man EIN File macht mit einer weiteren
Spalte, die die Systemgröße enthält)
w(t,L)L^-a
1
0.1
"roughL100.dat" u ($1/100**z):($2/100**a)
"roughL200.dat" u ($1/200**z):($2/200**a)
"roughL500.dat" u ($1/500**z):($2/500**a)
0.01
0.0001
0.001
0.01
0.1
t/L^Z
1
10
100
Im Allgemeinen sind die Skalenexponenten nicht bekannt, dann muss man – ausgehend von sinnvollen Startwerten – iterativ die Werte ändern bis die Kurven gut
übereinanderliegen (“Datenkollaps”).
2
10
Perkolation
Modell für poröses Gestein: Quader in kleine Würfel zerlegt, wo jeder Würfel mit
einer Wahrscheinlichkeit 1 − p von Stein “belegt” ist. Der Anteil p ist “frei”.
Frage: Wie groß muss p sein, damit Wasser von einer Seite durch den ganzen
Stein zur gegenüberliegenden Seite hindurchfließen (“perkolieren”) kann. → Phasenübergang bei kritischer Konzentration p = pc oberhalb der das Wasser hindurchfließt. Perkolation ist ein wichtiges (Spielzeug) Modell für Phasenübergänge
generell (mehr in Statistische Physik II). Vielen Phasenübergängen liegen (versteckte) Perkolationsübergänge zugrunde.
Literatur: [1].
___ ``___
`
`
`
_ ``_
`
ab
a
b
b
aab
a
b
a
a
b
a
b
b
YYZY ZZYYY \\[[
ccc ddccc
\[ d
Z
d
Z
d
YZ ZZY \[
[ \[\[\[ c ddc
\
ef
eefe feffeee d
f
f
f
gghg hhggg
h
hh hgh g
jij
i
j
iii jjiii
j
jj m
mnmn
n
m mnnmnmnm
n
GH
EF
lkl
kl
GH
EF
kkJI lklkllkkJI H
GG HGHGHHGG F
EE FEFEFFEE
l
H
F
III JJIII
J
J
JJ KL
KKL
L
K LKLKLKLK N
L
MN
MMM NMNNMMM
N
NN
^
]]] ^^^]]]
^
^
^
] ^] ooo ppooo
p
p
p
o
p pop
9
::
9:9
9DC 9::9::99DC
:
DDCC
C DDCCDC
D
=>
>
=== >=>>===
>
>;
>
<<;
;;;<<;<<;;
<<
P
OOP
P
OOPPOPOPOO
P
q
qqq t
sss rrqqq t
sss ttsss
q
r
qr
r
t
t
q t
s rrq t
s tts
t
t
qr
W
WWW XXWWW
X
W
X
W
v
X
W
WVUV
X
UU
vuvvuu X
u
uv
u
u
UUU XWVUVVUUU
u
u
U
v
V
u
u
U
u
v
v
V
V
5565 66555
6
66 656
5
A
BA
B
BBAA
BBAABA
BA
&&
33
%
34433 7
@@?
44
%&
34
7
78
??? @@?@@??? "
%%$# %&&%&&%%$# 3
3
3321 7
7
77 78878877
@
4321 88
3
7
@
&
4
4
8
!"
!
1
"
!!!""!!! $
### $$### 1
111 22111
2
"
2
1
"((
" $
$$ 1
2
2,,+ -
'
,
+
+,
'(
-
-.
,
+
+++ -
'' '(('(('' *
-
-- -..-..-,,+++ ..
+
,
(
.
))*
)
*
+
)) *)*))
** /
*
/// 0/0//
0
/
/
0
/0
/ S00/ T
0
TSTST
ST
S
ST
S
SS
T
TS
yz
y
Q
Q
z
z
R
R
S
yz
y
Q
Q
z
R
R
yy|
QQx
S~}
zyy|{
R
RQQxw }~
z
z
R
R
{|
w
}
{{{ ||{{{
www xxwww }
}}} ~~}}}
x
|
x
~
}~
||
xx }
~~
Abbildung 1: Perkolation in zwei Dimensionen: Es gibt einen Weg von freien
Gitterplätzen, so dass man durch das ganzen System laufen kann (gestrichelte
Linie). Das System perkoliert.
Der Wert von pc hängt von der Dimension des Systems und der Kristallstruktur
ab. In einer Dimension ist trivialerweise pc = 1. Für größere Dimensionen kann
man meistens keine analytischen Aussagen machen → Computersimulationen
(Ergebnisse quadratisches Gitter: pc ≈ 0.592746, kubisch: pc ≈ 0.3116, ... [1]).
Die dabei verwendeten Algorithmen (Clusteralgorithmen) kommen in VIELEN
Bereichen der computerorientierten Physik vor.
10.1
Stacks
Zur folgenden Implementierung benötigen wir einen speziellen Datentyp: Stacks.
Stack = Stapel, man kann ein Element oben drauflegen und wieder wegnehmen.
Nur das oberste Element ist zugänglich.
→ LIFO (last in first out).
Anmerkung: Warteschlange = FIFO Prinzip.
Realisierung: im Wesentlichen als Array.
Hier: objektorientierter Ansatz: Stacks = Objekte + Operationen für Stacks. Implementierung in Unterroutinen, Zugriff nur über diese (Datenkapselung).
C++ is eine Erweiterung von C, spezielle objektorientierte Unterstützung. Man
kann aber in JEDER Programmiersparche objektorientiert programmieren, aber
3
evtl. unpraktischer. Hier verwenden wir weiterhin C
Zugrundelegender Datentyp für Stacks von Elementen beliebigen aber gleichen
Typs:
typedef struct
{
int
num;
int
cap;
size_t elem_size;
void
*data;
} lstack_t;
/*
/*
/*
/*
current
size of
size of
pointer
num. of elements in the stack
a stack (No. of elements)
an element
to stack-memory
*/
*/
*/
*/
Grundlegende Operationen:
• new: Anlegen eines Stacks für Elemente einer bestimten Größe, mit einer
maximalen Zahl von Elementen.
• delete: Löschen eines Stacks.
• push: Ein Element wird oben auf den Stack gelegt.
• pop: Ein Element wir vom Stack runter genommen.
cap
cap
cap
num
num
cap
num
num
elem_size
new
elem_size
elem_size
delete
push
elem_size
pop
Implementierung:
/** Creates a stack of size ’cap’, where each data-element **/
/** has the size ’elem_size’ (in bytes = char).
**/
/** RETURN: pointer to the stack
**/
lstack_t *lstack_new(int cap, size_t elem_size)
{
lstack_t *stack;
stack = (lstack_t *) malloc(sizeof(lstack_t));
stack->num = 0;
stack->cap = cap;
stack->elem_size = elem_size;
stack->data = malloc(cap*elem_size);
return(stack);
}
4
/** Deletes a ’stack’
**/
void lstack_delete(lstack_t *stack)
{
free(stack->data);
free(stack);
}
Hinweis: Für push und pop wird immer ein Zeiger auf das Element übergeben.
/** Pushes an ’element’ on top of the ’stack’.
/** RETURN: =0 -> everything ok, or = LSTACK_FULL
int lstack_push(lstack_t *stack, void *element)
{
void *ptr;
**/
**/
if(stack->num >= stack->cap) /* Tests if stack is full */
return(LSTACK_FULL);
ptr = stack->data + (stack->num++) * stack->elem_size;
memcpy(ptr, element, stack->elem_size);
return(0);
}
/** Pops the top ’element’ from the ’stack’ **/
/** RETURNS =0 -> ok, or = LSTACK_FULL
**/
int lstack_pop(lstack_t *stack, void *element)
{
void *ptr;
if(stack->num == 0)
/* Tests if stack is empty */
return(LSTACK_EMPTY);
/** return the element to be poped: **/
ptr = stack->data + (--(stack->num)) * stack->elem_size;
memcpy(element, ptr, stack->elem_size);
return(0);
}
Literatur
[1] D. Stauffer und A, Aharony W.H. Press, S.A. Teukolsky, W.T. Vetterling,
Perkolationstheorie, (Wiley-VCH, Weinheim 1995)
5











