Analysis, Funktionslehre Funktion = Vorschrift, die jeder Zahl x

Analysis, Funktionslehre
Allgemein:
Funktion = Vorschrift, die jeder Zahl x genau eine andere Zahl zuordnet.
freier Fall: s(t)=5*t2
Druck:
p(T)=0.0037*T+1.013
s=Strecke t=Zeit
T=Temperatur p=Druck
e=Eulersche Zahl=2.718
y
2. Quadrant
-x
1. Quadrant
y5
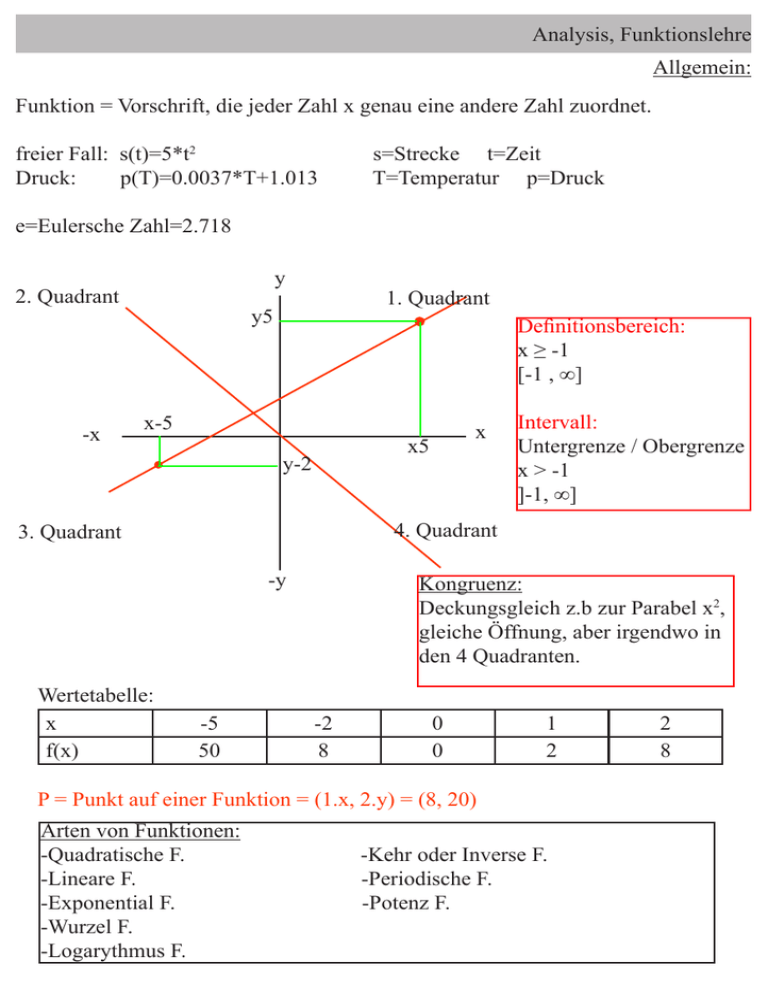
Definitionsbereich:
x ≥ -1
[-1 , ∞]
x-5
y-2
Intervall:
Untergrenze / Obergrenze
x > -1
]-1, ∞]
4. Quadrant
3. Quadrant
-y
Wertetabelle:
x
f(x)
x
x5
-5
50
Kongruenz:
Deckungsgleich z.b zur Parabel x2,
gleiche Öffnung, aber irgendwo in
den 4 Quadranten.
-2
8
0
0
1
2
P = Punkt auf einer Funktion = (1.x, 2.y) = (8, 20)
Arten von Funktionen:
-Quadratische F.
-Lineare F.
-Exponential F.
-Wurzel F.
-Logarythmus F.
-Kehr oder Inverse F.
-Periodische F.
-Potenz F.
2
8
Analysis, Funktionslehre
Taschenrechner:
-Variable speichern:
Wert / STO→ / Variablenname
-Variablen löschen:
F6 / Clear a-z
F4 / DelVar
-Auflösen nach x:
F2 / Solve
F3 / solve( und, (x,y))
-Funktion definieren:
F4 / Define f(x)=....
-Aufrufen:
y(20)
-Funktion löschen:
F4 / del Var
-mehrere Funktionen mit Graph:
◊ F1 = Funktion definieren
◊ F3 = Graph der Funktionen
F4 = anzeigen oder nicht anzeigen
◊ F2 = Anzeige optimieren
◊ F5 = Werteliste lesen
-Brüche zusammenfassen:
F2 / comDeanom
-Ausklammern:
F2 / factor
-Ausmultiplizieren:
F2 / expand
-Minimum, Maximum einer Funktion
F3 / fMin (2*x2+100*x,x)
F3 / fMax (-2*x2+100*x,x)
-Werte eingrenzen (mit Operator)
wenn nicht quadratisch:
-2*x2+100*x | x=25
bei quadratischen Funktionen:
fMin ( Formel , x ) | x<4 and x>2
fMax ( Formel , x ) | x>4 and x>2
Achtung:
fmin und fmax im TR nur
für quadratische Funktionen.
y( x ) = x 2 − 2 * x + 3
f min x = 1
f min y = +∞ −∞
Weil x-399 sein kann, y abber minimal bei x=1 liegt.
im Graphen:
F5 / Minimum / lower Bound / upper B.
F5 / Maximum / lower Bound / upper B.
-Ausgabe:
x = 2*e8*� + cos-1*(40)
e8 bedeutet eine natürliche Zahl oder Null.
x = 0 + cos-1*(40)
x= cos-1*(40)
-Scalierung des Graphen gleichmässig:
F2 / Zoom Dec
-Nur positive Werte bei Funktionen (oder min,
max usw,):
Catalog / abs()
Analysis, Funktionslehre
Graphen:
y
y
x
0
Exponentialkurve, Regressionskurve
2 Funktionen
y
y
x
0
x
0
Geraden (lineare Kurven)
periodische Kurve
y
y
x
0
x
0
x
0
Parabel
abklingende Schwingung
y
y
0
0
x
Exponentialkurve, Regressionskurve
Hyperbel
x
Analysis, Funktionslehre
Die Gearde (lineare Funktion):
implizierte Form = 2*x+y-1=0
explizierte Form (Normalform) = y(x)=5x-3
2*x-y=0
y(x)=2*x
y
3*x+2*y-7=0
y(x)=-2x+7
3 2
4
-x
-3
Schnittpunkt
0
x
2
-6
-y
Schnittpunkt = -2x+7 = 2*x
3 2
Normalform:
y(x) = m*x + q
Steigung = m
Verschiebung (Ordinatenabschnitt) = q
Steigung positiv = 1, 3 Quadrant
Steigung negativ = 2, 4 Quadrant
Liegen drei oder mehr Punkte auf einer Graden, so heisst das kollinear
Analysis, Funktionslehre
Berechnung der Steigung:
y
Achtung Richtung
und Vorzeichen
beachten!!!
←-x
→+x
↑+y
↓-y
B1(x,y)
Δy
B2(x,y)
α
Δx
0
-x
x
Steigung = m
m = tan α
∆y
m=
∆x
-y
Steigung = m
Steigung
in αProzent:
m = tan
m=
∆y
= 0.1 = Steigung 10%
∆x
m=
yB1 − yB2 yB2 − yB1
=
xB
y 1 − xB2 xB2 − xB1
m=
yB1 − yB2 yB2 − yB1
=
xB1 − xB2 xB2 − xB1
y
2
x
y=q
y=2
3
x=q
x=3
x
Analysis, Funktionslehre
Bewegungsabläufe:
s(t)
Weg /Zeit Funktion
∆s
V(Geschwindigkeit)=
∆t
s( t ) = V * t + s0
s0
∆s
∆t
t
Bewegungsrichtung:
0
-1
1
P→
positive Geschwindigkeit
Q←
negative Geschwindigkeit
ungleichförmige Bewegungen:
s
s
t
„Anfahren“ positive Beschleunigung
t
„Abbremsen“ negative Beschleunigung
s
beschleunigt
verzögert
t
Analysis, Funktionslehre
Die Parabel (Parabel zweiter Ordnung):
y
Grundform (allgemeine Form):
y(x) = a*x2 + b*x +c
a = Öffnung
c= Verschiebung in y
Scheitelpunktform:
y(x) = a*(x-u)2 + v
a = Öffnung
u = Verschiebung x
v= Verschiebung y
Symmetrieachse
min y = 2
0
x
Scheitelpunkt, auch Extemum.
Parabel gegen oben offen:
minimale x-Stelle
Grundform:
y(x) = (-a)*x2 + b*x +c
y
Parabel gegen unten offen:
maximale x-Stelle
max y = 5
0
x
Achtung:
fmin und fmax im TR nur
für quadratische Funktionen.
Symmetrieachse
y( x ) = x 2 − 2 * x + 3
f min x = 1
f min y = +∞ −∞
Weil x-399 sein kann, y abber minimal bei x=1 liegt.
Analysis, Funktionslehre
Scheitelpunktformel:
y
Symmetrieachse
min y = 2
x
0
b
Symmetrieachse = -2*a
Grundformel : y(x)=a*x 2 + b * x + c
Grundformel negativ gegen unten offen : y(x)=(-a)*x 2 + b * x + c
Scheitelpunktformel : y(x)=a*(x-u) 2 +v
 -b
4*a*c - b 2 

Scheitelpunkt: 
,
 2*a
4*a 
a = Öfffnung der Parabel
u= x-Verschiebung der Parabel
y(x)=a*(x+2) +1
y
a = Öffnung
u = Verschiebung x-Richtung
v= Verschiebung y-Richtung
Scheitelpunkt = S(u, v)
y(x)=a*(x-6)2+1
2
y(x)=a*(x-2)2+1
1
-2
←+u
0
2
→ -u
6
x
Falls kompliziert x ausklammern, um
quadratischen
vom linearem
Teil zu trennen!!
Analysis, Funktionslehre
Schnittmenge Parabel-Gerade
y
0
x
y(x)=x-3
y(x)=-0.5*x2+2*x
Schnittpunk = x-3 = -0.5*x2+2*x
ergibt 2 Resultate, weil zwei
Schnittpunkte
y
0
x
y
0
ein Schnittpunkt
Diskriminante D = 0
x
y
0
Zwei Schnittpunkte
Diskriminante D > 0
keinen Schnittpunkt, schneidet sicht
Diskriminante D < 0
x
Analysis, Funktionslehre
Schnittmenge Parabel-Gerade:
+
Sekante
y
0
x
Tangente, Teil der Sekante innerhalb eines Radiuses
Tangente oder Gerade,
berührt Radius nur
y
0
x
Zwei Geraden
die die Parabel
berühren.
Je ein Schnitt oder Berührungspunkt.
Bekannt Punkte einer Parabel der Grundform y(x)=a*x 2 + b * x + c
P(2,1)
Q(-1, 3)
R (3, 4)
1=a*22 +b*2+c
ß
1=a*22 +b*2+c
3=a-b+c
4=a*32 + b * 3 + c
ß
y(x)=
Þ a=
11 2 19
1
*x *x +
12
12
2
11
19
1
b=c=
12
12
2
Analysis, Funktionslehre
Formen von Parabeln:
y
a=1 Normalparabel
a=2 a > 1 dehenen, strecken ist
ist schmaler als Normalparabel
x
a=0.5 a < 1 pressen, stauchen ist
breiter als Normalparabel
y
x a=-1 Normalparabel
a=-2 a > 1 dehenen, strecken ist
ist schmaler als Normalparabel
a=-0.5 a < 1 pressen, stauchen ist
breiter als Normalparabel
Spiegelung
y
Die Parabel y(x)=-1/5*(x-2)2-1
wird über die x-Achse gespiegelt
x
Formel : y(x)=1/5*(x-2)2+1
y
Die Parabel y(x)=-1/5*(x-2)2-1
wird über die y-Achse gespiegelt
x
Formel : y(x)=-1/5*(x+2)2-1
Analysis, Funktionslehre
Linearfaktorzerlegung oder Nullstellen:
x
y
x2
x1
zwei Nullstellen
Grundform :
a *( x - x1 ) *( x - x 2 )
y( x ) = 3 * x 2 - 9 * x - 30
y(x) in ein Produk
kt zerlegen:
ß
eine Nullstelle
y( x ) = 3 *( x 2 - 3x -10)
y( x ) = 3 *( x - 5) * ( x + 2)
Nullstellen Þ
x1 = 5
0 = 3 * x 2 - 9 * x - 30
Þ
Achtung - wird +
Achtung + wird -
x 2 = -2
x1 = 5
x 2 =-2
keine Nullstelle
Analysis, Funktionslehre
Potenzfunktion
Potenzfunktion:
y(x) = a*xn
y
n ist gerade
x
a=1
a>1
1 >a <0
Parabel n-ter Ordnung
a bewirkt eine Stauchung
oder Streckung
y
x
a = -1
a < -1
-1 <a >0
a negativ bewirkt eine
Spiegelung an der x
Potenzfunktion:
y(x) = a*xn
n ist ungerade
a=1
a>1
1 >a <0
a = -1
a < -1
-1 <a >0
Analysis, Funktionslehre
die Hyperbel:
f (x) =
xn ungerade
y
1
xn
y
y
x
1
x = x3
1
x= x
x
x
1
x = x5
xn gerade
y
x
1
x = x2
y
y
x
x
1
x = x4
1
x = x6
Analysis, Funktionslehre
allgemeines
Funktion oder Gleichung 3. Ordnung:
y(x) = a*x3 + b*x2 + c*x + d
Horizontaler Wurf:
y( x ) = tan (d)* x -
5
v *cos (d)
2
2
* x2
v = Geschwindigkeit
x = Distanz
y = Höhe
d = Abschusswinkel
Wurf aus Höhe (Stein wird con Spitze Turm horizontal geworfen):
5
* x2 + h
2
v
v = Geschwindigkeit
h = Höhe
y( x ) = -
s( t ) = 5 * t 2
y= bei Weite x , y=0
h= Höhe des Turms
x= Weite
Analysis, Funktionslehre
Die Umkehrfunktion oder Inverse Funktion:
y
Bei der Kehrfunktion
werden die Kordinaten E R0
des Scheitelpunkts x
und y vertauscht.
z.B. (-3;5) ↔ (5;-3)
E R0+
-x
x
-y
Umkehrfunktionen werden
immer über die Gerade der
Winkelhalbierenden vom
1. und 3. Quadranten
gespiegelt.
Funktion f(x)=x 2
Kehrfunktion x=y 2
Diese Zuordnung ist nicht eindeutig:
Dies ergibt 2 einzelne Funktionen:
Umkehrfunktion:
y1 = x
f −1 (x)= − x
y1 = - x
x ≤ 0
x ∈ −0
y2 = − x
f -1 ( x ) = - x
-5
50
x ∈ +0
y1 = x
f -1 ( x ) = x
Wertetabelle:
x
f(x)
x ≥ 0
f −1 (x)= x
-2
8
0
0
1
2
2
8
0
0
2
1
8
2
x und y Werte werden vertauscht:
x
f(x)
50
-5
8
-2
Analysis, Funktionslehre
Die Umkehrfunktion oder Inverse Funktion:
Die Umkehrfunktion einer linearen Funktion:
6
Symmetrieachse
(1-3 Quadrant)
y
Bei der Kehrfunktion
werden die Kordinaten
y und y vertauscht.
z.B. (-3;5) ↔ (5;-3)
2
-x
-y
2
x
6
Funktion
f(x)=-3*x+6
Steigung m =
Dy
-3
=
Dx
1
Umkehrfunktion (x und y werden vertauscht) x=m*y+q
x=-3*y+6
Steigung m =
Dy
-1
=
Dx
3
Auflösung nach y
x-6
y=
-3
6-x
y=
3
1
y = - *x +2
3
Analysis, Funktionslehre
Die Umkehrfunktion oder Inverse Funktion:
y
Funktion :
y( x ) = x 3
Kehrfunktion :
x
-x
x = y3
y( x ) = 3 x
-y
f -1 ( x ) = 3 x
y
Funktion :
f ( x ) = x 2 +1
Kehrfunktion :
x
-x
x = y 2 +1
y 2 = x -1
1.Funktion :
-y
y = x -1
2.Funktion :
y = - x -1
Funktion :
y
2
f ( x ) = -x - 6 * x - 7.5
-x
x
Scheitelpunkt :
Umkehrfunktion1 :
S (-3;1.5)
y=
1.5 - x - 3
2
y ( x ) = -( x + 3) + 1.5
2
x = -( y + 3) + 1.55
-y
2
( y + 3) = 1.5 - x
y = ± 1.5 - x - 3
Umkehrfunktion 2 :
y = - 1.5 - x - 3
Analysis, Funktionslehre
Die Umkehrfunktion oder Inverse Funktion:
Funktion :
y
f ( x ) = -x
2
x ³0
x £0
Umkehrfunktion:
-x
x
-y
y
x= - y
2
1.Umkehrfunktion
2.Umkehrfunktion
y= -x
y= - -x
Achtung : y= - - y
Achtung : y= - - - y
Funktion :
f ( x ) = -( x - 3)
2
x ³0
x £0
Umkehrfunktion :
x x = -( y - 3) 2
-x
2
( y - 3) = -x
y - 3 = ± -x
-y
1.Umkehrfunktion :
2.Umkehrfunktion:
y=
y = - -x + 3
-x + 3
Analysis, Funktionslehre
Die Exponential- oder Logarythumsfunktion:
y
-x
x
-y
Achtung:
Bei der Exponential oder Logarythmusfunktion darf die Basis nie negativ
sein.
Sonnst ist es keine Funktion mehr.
f ( x ) =10x
y =10x
f(x)=2 x
y=2x
f(x)=ex
f(x)=ex
Umkehrfunktion
x =10y
y = log10 x
x=2y
y = log 2 x
x=e y
y = log e x
y=
log(x)
log(10)
y=
log(x)
log(2)
y=
log(x)
log(e)
Analysis, Funktionslehre
Allgemeines:
x
y
1
x -1
2
y : x---->
1
x -1
2
Definitionsbereich D:
Definitionsmenge sind die Zahlen des Definitionsbereichs.
Für Welche Werte ist die Funktion definiert? Können verarbeitet werden.
D = R \ {-1, 1}
D = {x € R | x \ -1,1}
D = {x € R | x ≠ -1,1}
Wertebereich W:
Welche möglichen Zahlen erhalten wir als Lösung?
f(ß) = sin(ß)
W = [-1, 1]
D=R
Intervallschreibweise:
f(x) = √x
D = {x € R | x ≥ 0} ----Intervallschreibweise [0, ∞) oder [0, ∞ [
Analysis, Funktionslehre
Differentialgleichung:
f(x)
f(x1)
∆f
f(x)
x
∆x
x1
x
a = f(t1) - f(t)
t1 - t
f(t) = a*(t1-t) + f(t1)
f(t) = f(t1) + a*t1 - a*t
Bsp :
f(2) = 5, f(4) = 1
f(x) = f(x1)+ a*(x - x1)
f(x) = 5 + a*(x - 2)
f(x) = 5 + - 2*(x - 2)
f(x) = - 2*x + 9
a = f(x1) - f(x)
x1 - x
a = 5-1
a = -2
2-4
Analysis, Funktionslehre
Differentialgleichungen:
s(t)
Zufluss 150 l/min 0.05%
s(t1)
∆s
5000 l
100kg Salz=
Lösung 0.02%
s(t)
Abfluss 150 l/min 0.05%
t
∆t
t+∆t
t
Definition: Die Funktion, die wir suchen und ihre momentane Änderungsrate
kommen als Unbekannte in der Funktion vor. Nicht Zahl ist gesucht, sondern
ganze Funktion.
∆s
f(t+∆t)-f(t)
=
∆t
∆t
s(t)
∆s = f(t+∆t) - f(t)
Salzkonzeentration = c(t)=
5000
t und ∆t eng beieinander
s(t+∆t)
≈ s(t) + ∆V*0.005 - ∆V*c(t)
s(t)
s(t+∆t)
≈ s(t) + ∆t*150*0.005 - ∆t*150*
/-s(t) :∆t
5000
s(t)
s(t+∆tt)-s(t)
≈ 150*0.005 - 150*
5000
∆t
s(t)
s(t+∆t)-s(t)
≈ 7.5 - 150*
5000
∆t
Grenzfall / Grenzwert (momentane Änderungssrate)
∆t 
→0
s'(t)=7.5 - 150*
s(t)
5000

y 
TR : deSolve(y'=7.5 - 150*
 and y(0)=0.2,x,y)

5000 
Analysis, Funktionslehre
Änderungsrate:
Q
f(t+∆t)
∆f
P
f(t)
∆t
2
Beispiel f(t)=t + 3 * t
t
t+∆t
mittlere oder durchschnittliche Änderungsrate (Differenzquotient):
∆f
f(t+∆t) - f(t)
=
∆t
∆t
im Zeitintervall [t,t+” t]
Geometrisch Steigung von P zu Q
momenntane Änderungsrate, Grenzfall:
Grenzwert für ∆t gegen Null! Grenzfall: Sekante wird zur Tangente. (Nenner wird 0)
1
f(t+∆t) - f(t) Grenzfall kann natürlich (nicht bestimmter F-Wert),
=
oder selber über ∆t bestimmt sein.
x-3
∆t
Geometrisch Gerade wird zur Tangente bei ∆t fast Null.
f(t+∆t) - f(t)
f(t+∆t) - f(t)
lim
→ f``(t) = lim
∆x→ 0
∆x→ 0
∆t
∆t
TR :
d ( t 2 + 3 * t , x)
out "Momentane Änderungsrate" 2*x+3 bei lim Resultat 3
∆x→0
Funktion der Änderungsrate der Funktio
on.
TR:
limit (
f(t+∆t) - f(t)
, x, 0) bestimmt den Y-Wert an dem angegebenen X-Wert,
∆t
Out: y-Wert des Grenzwertes.
Analysis, Funktionslehre
Grenzwert:
Beispiel:
2 * x2 − 7 * x + 3
x −3
( x − 3) *(2 * x −1)
f ( x) =
x ∈ \ {3}
x −3
Schreibweise :
( x − 3) *(2 * x −1)
x0 = 3 lim f(x)=
x →3
x −3
f (33) = 7
f ( x) =
( x − 3) *(2 * x −1)
, x ≠3
x −3
7 , x=3
rechtsseitiger Grenzwert:
lim+ Grenzwert von der positiven X-Achse her.
f(x) =
x→3
linksseitiger Grenzwert:
lim− Grenzwert von der negativen X-Achse her.
x→3
f(x) ist stetig, wenn sie keine Sprungstellen bei
möglcihen Grenzwerten x0 hat.
Funktion ist mit einem Strich gezeichnet.
Extemum
Änderungsrat=0
7
4
3
Achtung:
Ausgefüllte
Kreise dominieren
Analysis, Funktionslehre
Rechnen mit Matrixen im TR:
0

1

2

3

4
5

6

7

8


4

 ∆ eines Wertes immer ein Wert minus den vorherigen Wert.
8

16 

32 

Ist die Änderungsrate bekannt, so kann mit:
64 
deSolve y‘= Term and y(0)=Wert, x, y


132 
oder

Integrale Term, x ACHTUNG: +C
264 

528 

1048 
Bei Listen immer zuerst

x Liste, dann y Liste
subMat (Matrix-name, erste_Zeile, Spalte, letzte_Zeile, Spalte)
Erstellen einer Matrix:
[3,2;4,5;.......] ->Sto Matname
[[3,2][4,5].....]->Sto Matname
Änderungsrate:
subMath∆1 ./ subMath∆2
Rechnen mit Listen o. Matrixen: + .* ./
z.B: Listen_o._Matrixname subMath() - subMath()
Grösse einer Matrix ermitteln: rowDim(Name_der_Matrix)
Liste aus matrix erstellen:
mat>list(subMath())->Sto Listenname
mat>list(Math_Name)
Liste erzeugen:
Regressionskurve:
{2,4,7,9,10.......}->Sto Listenname
Linreg ListeX, ListeY
Gerade
Quadreg ListeX, ListeY
Parabel
a, b der Funktion:
ShowStat
Minimum Matrix oder Liste: min (Name_Liste_oder_Matrix)
Maximum Matrix oder Liste: max (Name_Liste_oder_Matrix)
bestmögliche Koeffizienten auf der Parabel
ntegriernQuadreg
a*t2 + b*t +c a, b, c
:
regeq(x)
Plotten von Punktwolken:
Apps / Data-Matrix Editor / new
Liste C1 anwählen
Liste C2 anwählen
F2 plot setup
F1 define
Analysis, Funktionslehre
Integrieren:
F3
ƒ( integrate
ƒ(term, x)
ƒ(term, x, Anfangswert, Endwert)
Achtung: TR liefert nur eine Stammfunktion mit c=0
Quadreg(Wie Linreg aber bei Qudratischen Funktionen): Quadreg Liste1, Liste2
Limit, um den Grezwert der nichtdefinierten Stelle zu ermiteln:
limit(Term, x, Stelle, 1 oder -1) /-1 für linkseitig 1 für rechtsseitig
limit(Term,n,n=∞)
Σ( sum: Konstante*Σ(Term, i, Startwert, Endwert)
Integrieren: ƒ(Term,x,Anfangswert,Endwert)
Änderungsrate: δ(f(x),x,wievielte Ableitung)
Differenzgleichung: deSolve(y‘=f(x,y) and y(0)=y0, x, y)
Linearisierung durch Parabel: taylor (f(x), x, 2, x0) 2=Grad des Polynoms
Analysis, Funktionslehre
Regressionskurve:
Drei Punkt (1/1), (2/2), (4/5)
Gerade im TR: Linreg {1,5,4}, {1,2,4 }
4
y
Punktwolke
2
1
5
x
2
1
Die Regressionsgerade ist die Gerade durch die Punktewolke, bei der die Abstände
der Punkte zur wirklichen Gerade möglichst klein ist. Um Vorzeichenfehler zu vermeiden, nimmt man den tatsächlichen Funktionswert-den Punktwert im Quadrat.
jede Regressionskurve geht durch den Schwerpunkt.
SSE (sum squared error):
x1 + x 2 + x 3 ..... 1+2+4
7
=
=
Anzahl x
3
3
y + y 2 + y3 ..... 1+2+5
8
=
Schwerpunkt y = 1
=
Anzahl y
3
3
 7 8
Schwerpunkt ( x , y) =  , 
 3 3 
Schwerpunkt x =
Steigung y = m*x + b ⇒ b = y - m*x
8
7
b = - m*
3
3
SSE ( sum sqared error)
3
∑ (f(x
k=1
k
)-y k ) 2 = (f(1)-1) 2 + (f(2)-2) 2 + (f(4)-5) 2
tatsächlicher Funktionswert- Punktwert
f ( y) = m * x + b
Schwerpunkt
Analysis, Funktionslehre
((m*1+b) - 1) 2 + ((m*2+b) - 2) 2 + ((m*5+b) - 5) 2
8
8
8
7
7
7
((m*1+  -m*  ) - 1) 2 + ((m*2+  -m*  ) - 2) 2 + ((m*5+  -m*  ) - 5) 2
 3
 3
 3
3
3
3
9*m 2 -
52*m
26
+
3
3
für welches m ist SSE(m) minimal??? SSE'(m)=0
SSE =
n
∑ ( f (X
i=1
2
i
) − yi )
 


52*m
26
TR: solve δ 9*m 2 +
, m = 0 , m

 

3
3

out m, mit m b berechnen
Euler Verfahren (Differential 1. Ordnung):
gegeben :
f '( x) = cos( x), f(0)=2
gesucht:
f(x)=????
für x=0 habeen wir die Information f(0)=2 und f''(0)=1
für x=0.4 holeen wir die Information f''(0,4)=0,29
f(0.4)=??, D =h*f''(0)=0.4, f(0.4) » 2+Dy = 2,4
y1 - y0
h
y1 = y0 + h * f '(0)
f '(0) =
y1
Näherung für f(0,4)
y0 =2
h
0,4
x0 = 0
x1 = x0 +h
x2 = x1 + h
....
y0 = 2
y1 = y0 + h*f‘(x0)
y2 = y1 + h+f‘(x1)
......
xn = xn-1 + h
yn = yn-1 + h*f‘(xn-1)
je kleiner h, desto genauer die Kurve!!!
Analysis, Funktionslehre
das Summenzeichen Σ:
1
7
ån
=
n=3
Endweite
å
1 1 1 1 1
+ + + +
3 4 5 6 7
Die Operationen werden der arythmetik
zusammengezählt.
Operation
Schrittweite
Schwerpunkte:
C
verknüpfte Integrationsregeln:
b
∫
S
a
∫ (c * f (x))dx
a
b
Q
∫
a
S
b
∫
a
P
S
= ∫ (f ( x )dx ±
a
b
B
A
b
(f ( x ) ± g( x))dx
b
∫ g(x))dx
a
b
=c * ∫ f ( x )dx
a
grösster Re Wert der Inversion
von g
a
ist
Q,
weil
P
der
klein
n
ste
Abstand
f ( x )dx
=- f ( x )dx zu 0
1
b
wenn P am kleinsten,
nimmt Q den grösssten
b
c
P
Realen
Wert
an.
f ( x )dx
+ f ( x )dx
= f ( x )dx
∫
∫
S = ( x | y)
a
∫
c
 x1 +..... +xn y1 +.......+yn 
S = 
|



n
n
Differenzieren Integrieren:
gegeben y(x) = x*sin(α )
gesucht Y(x) so dass Y'(x)=x*sin(x)
man kennt nur die Änderungsrate von Y(x)
Lösung: Y(x)=
= òx*sin(x)*dx = sin(x)-x*cos(x) + C (Integrationskonstante)
Eine Funktion mit F‘ =f heisst Stammfunktion
Menge aller Stammfunktionen von f heissen unbestimmtes Integral
f heisst Integand.
/ steht für unbestimmtes Integral
Analysis, Funktionslehre
differenzieren
f '( x)
differenzieren
δ((.....,x)
←←←
→→→ f ( x)
←←←
→→→ F(x) Stammfunktion
integrieren
integrieren
∫ (.....,x)
Differenzieren:
gegeben :
f ( x) = sin(3 * x)
gesucht :
TR :
Out :
die Änderungsrate
δ (sin(3 * x), x)
f '( x) = 3 *cos( x)
gegeben :
f '( x) = −2 * x * y 2
f ( x, y ) = − 2 * x * y
y ( 0) = 1
2
TR :
deSolve( y ' = −2 * x * y 2 and y (0) = 1, x, y )
Out :
y ( x) =
1
x +1
2
 1

Kontrolle : δ  2
, x
 x + 1 
2
 1 
Out : −2 * x *  2
 x + 1
Integrieren:
gegeben :
f ( x) = sin(3 * x)
gesucht :
f(0)=C
alle Funktionen F(x),die die Eigenschaft haben, dass G'(x)=f ( x)
TR :
∫
Out:
(sin(3 * x), x)
-cos(3*x)
Stammfunktion von f (TR liefert nur Stammfunktion)
3
-cos(3*x)
+C (Integralkonstante)
3
Menge aller Stammfunktionen heisstt unbestimmtes Integal
Analysis, Funktionslehre
Rechenregeln für die Ableitungen (differenzeren):
f ( x) = x r
f ( x) = sin( x)
→ f '( x) = r * x r−1
→ f '( x) = cos( x)
→ f '( x) = − sin( x)
f ( x) = cos( x)
f ( x) = e x
→ f '( x) = e x
1
→ f '( x) =
x
f ( x) = ln x
Summenregel:
f ( x ) = g ( x ) + h( x )
→ f '( x) = g '( x) + h '( x)
Produktregel:
f ( x) = c * g ( x)
f ( x ) = g ( x ) * h( x )
→ f '( x) = c * g '( x)
→ f '( x) = g '( x) * h( x) + g ( x) * h '( x)
Quotiientenregel:
g ( x)
f ( x) =
h( x )
→ f '( x) =
g '( x) * h( x) - g ( x) * h '( x)
2
( h( x ))
Kettenregel:
f(x)=g (h(x))
→ f '( x) = g'(h(x)) * h'(x)
Äussere abgleietet von der Inneren, mal die Innere abgeleitet
Bei mehreren Ineinader:
a(b((c(d(x))))
→ a '(b(c(d ( x)))) * b '(c(d ( x))) * c '(((d ( x)) * d '
Achtung Konstanten:
4+x wird differenziert zu 1 (1*x0)=1*1
y+x=4 y‘+x‘=0
Eine Funktionsreihe der Gestalt:
∞
∑a
k =0
k
* ( x − x 0 )k heisst Potenzreihe.
a 0 , a1 , ... heissen Koeffizienten der Potenzreihe
x 0 heisst Entwicklungspunkt
a
Achtung :
Analysis, Funktionslehre
1
1
wird differenziert zu -1* 2
x
x
f ( x) = 2 x
711 = e11*ln 7
f '( x) = ln 2 * e x*ln 2
35 = e5*ln 3
f ( x) = e x*ln 2
= f '( x) = ln 2 * e x*ln 2 = f '( x) = ln 2 + 22
f ( x) = 7 x = f '( x) = ln 7 * 7 x
f ( x) = e x = f '( x) = ln e * e x
y * e3*x -5* y -2
f '( x) = 3 * y * e3*x -5* y -2
f '( y )
y
= 1
e3*x -5* y -2 =
- 5 * e3*x -5* y -2
Prr odukteregel : -5 * y * e3*x -5* y -2 + e3*x -5* y -2
Achtung:
b*ea*x = a*b*ea*x /bei e hoch kann der Exponent nach vorne genommen werden, bleibt aber im hoch.
Bei Wurzel √x2-3 /Zwei Funktionen
Konstanten = Null
implizit differenzieren:
x2 + y 2 = 1
/()' wobei y= (y(x) )
2
Produkteregel
2*x+2*y'(x)*y(x)=0
-2 * x
-xx
y '( x) =
=
2* y
y
1.Funktion y(x)
2.Funktion x 2
Analysis, Funktionslehre
Rechenregeln für die Integration:
Konstanten ≠ Null
Bsp :
Funktionsreihen:
für den Grenzwert, falls er existiert f(x)
k −1
 1 
− 
∑
 8 
k =1 
1
a = 1, q = −
8
16
8 16 32
8
+ + + ... a= , q = 9
8
3 9 27
3
3
23
1
0, 2323232323 a=
,q =
100
100
∞
∞
k −1
f ( x ) = ∑ (cos( x ))
k =1
a =1
q=x
ε15 an der Stelle x = 3
ε15 =
1
a
n
15
*q =
* cos( 3)
1− q
1 − cos( 3)
Hauptsatz der Differenzial und Integralrechnung:
Funktionsreihen:
für den Grenzwert, falls er existiert f(x)
∞
k −1
f ( x ) = ∑ (cos( x ))
k =1
a =1
q=x
ε15 an der Stelle x = 3
Analysis, Funktionslehre
das Summenzeichen Σ:
7
1
∑n
1 1 1 1 1
+ + + +
3 4 5 6 7
=
n=3
Endweite
∑
Die Operationen werden der arythmetik
zusammengezählt.
Operation
Schrittweite
TR:
Konstante*Σ(Term, i, Startwert, Endwert)
Σ(1/k!), k, 0, ∞) →Zahl durch Null wird berücksichtigt
Limit(Term, n, ∞) oder Limit(Term, n)|n=Schrittweite
Achtung:
Σ(Term, i, Startwert, Endwert)|n=Schrittweite
Bei Wurzelterm muss Schrittweite definiert werden, ∞ geht nicht.
1
1 1
1
π2
= 1 + + .... + 2 =
∑
2
4 9
6
n
n=1 n
∞
∞
1
∑n
n=0
2
1 1 1
= 1 + 1 + + + + .... = e
2 6 24

 n−1
lim ∆x * ∑ g ( xi ) = bestimmtes Integral von g(x) in den Grenzen a und b:
 i=0
∆x→ 0

b
∫ g ( x)dx
∆x =
a
n−1
b−a
n
π * ∑ f ( x) 2 * ∆x
k =0
b=Schluss
∆x → 0
π
∫
a=Anfang
f(x) 2 * dx
Analysis, Funktionslehre
Rotationskörper ,Matelflächen, Funktionsflächen ,Kurvenlängen usw.:
Kegelvolumen Vn :
n−1
π * ∆x * ∑ f ( xi ) 2
∆x =
i =0
h(Betrag auf der X-Achse)
n
Euler y n :
n−1
y0 + ∆x * ∑ f ( xi )
i =0
Kurvenlänge s n :
n−1
∆x * ∑ 1 + ( f '( xi )) 2
i =0
theoretischer Mittelwert t :
n
≈ ∆x * ∑ f (ti ) * ti
i =1
Beispiel Rotationskörper Kegelvolumen:
Volumen =
∆x =
r
x0 ∆x ∆x ∆x ∆x
h
h
n
1
*G * h
3
n−1
π * ∆x * ∑ f ( xi ) 2 ,
i =0
=
1 2
*r *π *h
3
∆xx =
h
n
h
π * * ∑ f ( xi ) 2
n i =0
n−1
Der Kegel wird in zylindrische Scheiben zerlegt. Die Summe der Einzelvolumen wird
zum Kegelvolumen, wenn wir die Schrittweite (oder ∆x) gegen unendlich gehen
lassen.
Analysis, Funktionslehre
bestimmte Integralfunktionen:
Fläche zwischen Graphen und x-Achse A, f(x) ≥ 0:
b
A = ∫ f ( x )dx
a
Differentia lg leichung :
x
y ( x ) = ∫ f (u )du
x0
Volumen bei Rotationsskörpern:
b
V = π* ∫ f 2 ( x )dx
a
Länge s des Graphen:
b
s = ∫ 1 + (f '( x ))2 dx
a
empirische Mittelwert x:
ar
x= ∫ x * f ( x )dx
a0
Mantelfläche M:
b
M = 2 * π * ∫ f ( x )* 1 + (f '( x ))2 dx
a
Analysis, Funktionslehre
bestimmtes und unbestimmtes Integral:
Achtung:
Integralrechnung nicht nur für Flächen, auch für Körper usw.
Hauptsatz:
Endpunkt
∫
Funktion dx
bestimmtes Integral ohne Konstante C
Anfangspunkt
unbestimmtes Integral mit Konstante C
ist F'=f un
nd f stetig, dann
b
∫
f ( x)dx = F (b) − F (a )
F '( x) = f ( x)
=
a
verknüpfte Integrationsregeln:
b
∫
b
(f ( x ) ± g( x))dx
a
b
∫ (c * f (x))dx
a
b
∫ f (x)dx
a
b
∫ f (x)dx
a
= ∫ (f ( x )dx ±
a
b
∫
g( x ))dx
a
b
=c * ∫ f ( x )dx
Flächenbereechnung:
Achtung Absolutwerte für
Flächen unter der x Achse.
grösster Re Wert der Inversion von g
ist Q, weil P der klein
nste Abstand zu 0
1
wenn P am kleinsten, nimmt Q den grösssten
P
Realen Wert an.
a
a
=- ∫ f ( x )dx
b
b
c
= ∫ f ( x )dx
+ ∫ f ( x )dx
c
a
Werkzeuge der Analysis:
Bestimmtes Integral (ohne Integrationskonstante C):
Formulieerung:
Bestimmtes Integral von y(x)
Ende
Mathematische Schreibweise:
∫
y ( x)dx
Anfang
TR:
∫ (y(x),x,Anfangswertt,Endwert)
Anwendungen:
Flächeninhalt, Volumen, Bogenlänge, Mantelfläche,
Mittelwerte einer Dichttefunktion,
Abstand von zwei Funktionen
Analysis, Funktionslehre
Mittlere Änderungsrate:
Formulierung:
Mittler Änderungsrate einer Funktion y(x) im
Intervall [x,x+
+Dx]
Dy
Mathematische Schreibweise:
Dx
TR:
Anwendungen:
Durchschnittsgeschwindigkeit,
Durchschnittsbeschleunigung,,
Durchschhnittskosten,.........
Momentane Änderungsrate:
Formulierung:
Momentane Änderungsrate einer Funktion y(x) an
derStellex
Mathematische Schreibweise: y '( x)
δ (y(x),x)
TR:
Tangentensteigung, Momentangeschwindigkeit,
Anwendungen:
Momentanb
beschleunigung, Regression
Unbestimmtes Integral, Stammfunktion (mit Integrationskonsttante C):
Formulierung:
Unbestimm
mtes Integral von y(x)
Mathematische Schreibweise:
òy( x)dx + C
TR:
ò(y(x),x)
Anwendungen:
bestimmte Integralee, Momentangeschwindigkeiten
Momentanbeschleunigung
Differntialgleichung:
Formulierung:
Differentialgleichung 1. Ordnung mit Anfangsbedingung
Mathematiische Schreibweise: y ' = f ( x, y ), y ( x0 ) = y0 , y ( x) = ?
TR:
Anwendungen:
deSolve( y ' = f ( x, y ) and y (0) = y0 , x, y )
Beliebig viele Problemstellungen in der Mathematik,
Physik, Biologie, Wirtschaftswissenschaften,.......
Analysis, Funktionslehre
allgemein wichtiges:
∆y
ist immer Tangens
∆x
m2 − m1
tan δ =
bei 90° = m1 * m2 = −1
1 + m2 * m1
y
Änderungsrate
b
∫ dx
α
v.Hand integrieren ( Wert von b) - ( Wert von a )
a
b
∫
dx geht nur in der Form von
i =1
a
TR eingabe:
1
*x
→ STO
3
n−1
∑ f (x
i
f(x)
Konstanten*dx*∑ ( f (i * dx) 2 , i, 0, n −1)
limit (Term, n, n = ∞)
∆x =
b−a
n
α
x
Analysis, Funktionslehre
Ortsvektor:
y
r
Punkt P
x
Grundform der geometrichen Reihe:
a = 30
q = 0, 7
∞
∑ 30 * 0, 7
k −1
k =1
a = 2 , Re ihe = 2 2*q = −
3
2
Bei komplizierten Funktionen ist die Funktion in eine
Orts-Zeit Funktion umzuwandeln, bei der ein Punkt P
in zeitlicher Abhängigkeit sich auf der Kurve bewegt.
Mathematisch: Parameterdarstellung einer Kurve
t:Parameter
Physikalisch: Ort-Zeit Funktion eines Massepunktes
t:Zeit
3
q=?
2
TR:
Mode / Graph / Parametric
Graph / xt1=? xt2=? ......
Analysis, Funktionslehre
hyperbolische Funktionen oder Hyperbelfunktionen:
sinh(−x ) = − sinh x
e x − e−x
2
x
e + e−x
cosh x =
2
sinh x
tanh x =
cosh x
cosh x
coth x =
sinh x
sinh x =
cosh(−x ) = cosh x
sinh( x + y ) = sinh x * cosh y + cosh x * sinh y
cosh( x + y ) = cosh x * cosh y + sinh x * sinh y
cosh 2 x − sinh 2 x = 1
(sinh x )' = cosh x
(cosh x)' = sinh x
1
(tanh x )' =
cosh 2 x
lineare Approximation:
l(x)=f(a)+f‘(a)(x-a)
a
x0
Linearisierung von f an der Stelle a ----- l(x)=f(a)+f‘(a)(x-a)
Für eine Parabel als Linearfunktion:
l(x) = a*x2 + b*x + c
l(x0) = f(x0)
l‘(x0) = f‘(x0)
l‘‘(x0) = f‘‘(x0)
TR:
taylor (f(x), x, 2, x0)
2=Grad des Polynoms
Analysis, Funktionslehre
Taylor-Reihen:
T( x ) = a 0 + a1 * ( x − x 0 ) + a 2 * ( x − x 0 )2 + a 3 * ( x − x 0 )3 + ....... + an * ( x − x 0 )n
f ( x 0 ) = T( x 0 )
f '( x 0 ) = T '( x 0 )
f ''( x 0 ) = T ''( x 0 )
f n ( x 0 ) = Tn ( x 0 )
a0 = f ( x0 )
a1 = f '( x 0 )
f ''( x 0 )
2!
f '''( x 0 )
a3 =
3!
f ''''( x 0 )
a4 =
4!
n
f ( x0 )
an =
n!
n ! = Fakultät
TR: !
a2 =
f k * ( x0 )
* ( x − x 0 )k
∑
k!
k=0
n
→M
M→
Zahl = δ * m * Be
L = Anzahl Ziffern
δ = Vorzeichen
B = Basis
e = Exponent
m = Mantisse
z1
z2
zL
L
m= +
+ ... +
= ∑z *B
Achtung:
B B
B
M (B, L, e , e ) ist
der Maschinenzahlen
Bei Taylorreihe
zuMenge
Potenzreihe
-> fakultäten belassen
2
0
L
j=1
j
−j
1
e0 , e1 = Bias Exponentenverschiebung
Bias = Verschiebung des Exponenten e − Bias = eiggentlicher Exponent
normalisert = führende Zahl 1.Ziffer ≠ 0
maxreal = B e1 * (1 − B−L )
e0 −1
Analysis, Funktionslehre
Graphen und ihr Verlauf:
f‘(x)>0 für alle x Werte des Intervalls :
streng monoton wachsend im Intervall
f‘(x)<0 für alle x Werte des Intervalls :
stren monoton fallend im Intervall
f‘(x)=0 Extremalstelle Lokales Minimum oder Maximum.
Vorzeichenwechsel eines Faktors ist entscheidend:
Bsp. f‘(x)=12*x3-12*x2-24*x
f‘(x)=12*x*(x-2)*(x+1)
kritische Stellen:
-1
0
f‘(x)=0
2
c
Linkskurve:
f‘ von - zu + (0 an der Stelle c)
links von c monoton fallend
rechts von c monoton steigend
lokales Minimum bei c.
c
Rechtskurve:
f‘ von + zu - (0 an der Stelle c)
links von c monoton steigend
rechts von c monoton fallend
lokales Maximum bei c.
c
c
Sattel:
beidseitig von c monoton
steigend
Sattel:
beidseitig von c monoton
fallend
Analysis, Funktionslehre
kein definierte Änderungsrate:
c
f‘ an der Stelle c nicht
definiert.
c
f‘ an der Stelle c ist ∞.
Wendepunkte:
f‘‘(x)<0 alle x vom Intervall sind rechtsgekrümmt
f‘‘(x)>0 alle x vom Intervall sind linksgekrümmt
f‘‘(x)=0 Wendepunkt
f‘(c)=0 und f‘‘(x)<0 lokales Maximum
f‘(c)=0 und f‘‘(x)>0 lokales Minimum
f‘‘(x)=0 Wendepunkt der Kurve
f‘(x)=0 lokales Mini- oder Maximum
Analysis, Funktionslehre
Implizit Differenzieren:
Bei x und y im Term -------> implizit differenzieren!!!
f (k ) * ( x0 )
* ( x − x 0 )k
k!
k =0
n
Tn ( x ) = ∑
1
* xk
k =0 k !
∞
e =∑
x
ak
für jedes x ∈ ℜ
(−1)k
* x 2*k
k =0 ( 2 * k )!
∞
cos( x ) = ∑
für jedes x ∈ ℜ
(−1)k * xk +1
k +1
k =0
∞
ln(1 + x ) = ∑
(−1)k
Berührungspunkte
sin( xGerade
) = ∑und Funktion:
* x 2*k +1
k =0 ( 2 * k + 1)!
∞
für x < 1
für jedes x ∈ ℜ
D<0 = kein Berührungspunkt,
keine
Extremalstelle
k
∞
(−1)
1
* x 2*k +1 für x
)
+ 1Extremalstelle
D=0 = ein Berührungspunkt
eine
k =0 ( 2 *, k
∞
1
=
für x ∈ (−1 1)
xk
D>0 = 2 Schnittpunkte
∑
1 − x k =0
arctan( x ) = ∑
Achtung:
Ableitung * Ableitung =tang
-10*(-2-x)2 = -10*(x+2)2
-10*(-2-x)3 = 10*(x+2)3
Bei Integral mit ABS() rechnen.
Analysis, Funktionslehre
Tangente prallel zur z-Achse und soll die Fläche
-x2+4
in zwei glleiche Teile schneiden:
2
u
u*(-u + 4) + ∫
2
2
u
2
1
-x + 4 = * ∫ -x 2 + 4
2 0
2
2
y = −u + 4
Tangente g soll Parabel berühren
und der x-y Abschnitt solll minimal sein.
(0/ )
Länge=d
P(u / 4-u2)
f(x)=4-x2
g
u
( /0)
g : y = f (u ) + f '(u )( x − u )
y = 4 - x2 − 2 * u( x − u)
Schittpunkt der Achsen:
y-Achse
: x=0
y=4+u 2
x-Achse
: y=0
x=
2
4+u 2
2*u
 4+u 2 
2
 + (4+u 2 )
d (u ) = 
 2*u 
v
x1
x2
P(x)=a*(x-x1)*(x+2)
u
P(x)=a*(x-u)2+v
Analysis, Funktionslehre
Asymtoten:
Eine Asymtote ist eine Geard, der
sich der Grap h einer Funktion F(x)
unbegrenzt nähert bei immer grösser
werdendem x an eine Zahl, die nicht
zum Definitionsbereich von f gehört.
a
Asymtote( x) = m * x + b
lim f ( x) − (m * x + b) = 0
x→∞
manchmal : m = lim f '( x)
x →∞
lim
f ( x) = ±∞
lim
f ( x) = ±∞
x→ a +
x → a−
oder/und
Analysis, Funktionslehre
Umkehrfunktion:
2
x und y Werte werden vertauscht:
Bsp.
1

f −1 ( f ( x)) = f −1  * x − 3 =
 2

1
1
2
1
y ( x) = * x − 3
2
x( y ) = 2 * y + 6
1

f −1 ( x) = 2 * * x − 3 + 6
 2

Eine Funktion f(x) heisst umkehrbar, wenn aus x1 ¹ x2 stest folgt f(x1) ¹ f(x2).
Wird als Umkehrfunktion oder Inverse Funktion bezeichnet.
Symbol:
x = f -1 ( y )
y ist jetzt sie unabhängige Variable, x sie Abhängige.
Im gewohnten Kordd
dinatensystem: y = f -1 ( x)
Umkehrfunktionen werden immer über 45° des ersten und dritten Quadranten
gespiegelt.
Umkehrfunktionen Arcus- und Areafunktionen:
Arcusfunktionen : sin-1, cos-1, tan-1 man fragt nach dem Bogen y (Arcus),
dessen Sinus Cosinus oder Tangens x ist.
Areafunktionen : Umkehrfunktion der Hyberbolischen Funktionen
y=arsinh(x) (lies: area sinus hyperbolicus x)
y=arcosh(x), y=artanh(x), y=arcoth(x)
Analysis, Funktionslehre
Von Hand Integrieren:
Funktionsreihen:
für den Grenzwert, falls er existiert f(x)
∞
dx
k −1
f ( x ) = ∑ (cos( x ))
df
k =1
a =1
q=x
ε15 an der Stelle x = 3
ε15 =
a
1
n
15
*q =
* cos( 3)
1− q
1 − cos( 3)
∆y df
df ( x )
f '( x ) =
=
bzw.
∆x dx
dx
df
f ( x) = x3 →
= 3 * x2
dx
bzw.
d
f(x)
dx
bzw.
d 3
x
dx
x
Substitutionsmethode:
Bei einem besimmten Integral kann auf die Rücksubstitution verzichtet werden,
wen man die Integrrationsgrenzen der Substitutinsgleichung mitsubstituiert.
b
g(b)
a
g(a)
∫ fg(x)) * g '((x)dx = ∫
f (u )du
Bsp.
π
2
∫ sin(x)
4
* cos( x ) * dx
0
Substitution:
du
= cos( x ),
dx
u = sin( x ),
unter Grenze: x = 0
u = sin (0) = 0
π
obere Grenze: x =
2
π
u = sin   = 1
 2 
π
2
∫
0
1
sin( x )4 * cos( x ) * dx = ∫ u 4 * cos( x ) *
0
dx =
du
cos( x )
1
1
du
= u 4 * du = u 5
cos( x ) ∫0
5
1
0
mit Rücksubstitution :
π
2
∫ sin(x)
0
4
π
2
* cos( x ) * dx = ∫ u 4 * cos( x ) *
0
1
Rücksubstitution := sin( x )5
5
1
1
1
*∫
y + 12
2
1
Substitution u = y +
2
1
1
1
* ln u + C
*
=
2 ∫ u
2
Rücksubstitution :
1
1
= * ln y + + C
2
2
∫ 2* y + 2
∫ fg(x)) * g '((x)dx = ∫ f (u)du
π
2
0
π
2
1
du
= u 4 * du = u 5
cos( x ) ∫0
5
π
2
0
=
Analysis, Funktionslehre
∫
xr
∫
1
x
=
= ln x + C
∫ sin(x)
∫ cos(x)
∫e
x
1
∫ 1+ x
2
∫ sinh (x)
∫ cosh (x)
1
∫ cos (x)
2
∫
∫
∫
∫
1
* xr +1 + C
r +1
1
1 − x2
1
x2 + 1
1
x2 −1
1
1 − x2
= − cos( x ) + C
= sin( x ) + C
= ex + C
= arctan( x ) + C
= cosh (x) + C
= sinh (x) + C
= tan (x) + C
= arcsin (x) + C
= arcsinh (x) + C
= arccosh (x) + C
= arctanh (x) + C
∫ (g(x) + h(x))
∫ (a * g(x))
=
=
∫ g ( x ) + ∫ h( x )
a * ∫ g( x )
Substitutionsmethode
π
∫ 2 * x * cos( x
2
)* dx
0
x 2 wird durch y ersetzt
dy
= 2* x
dx
dy = 2 * x * dx
y'=
π
∫ 2 * x * cos( x
0
π
2
)dx = ∫ cos( x 2 )* 2 * x * dx =
0
= sin( y ) + C = sin(π) −ssin(0)
y( π)
∫
y(0)
π
cos( y )dy =
∫ cos( y )dy
0
Partielle Integration:
Analysis, Funktionslehre
Der Integrand f(x) wird in "geeigneteer" Weise in ein Prdukt aus zwei
Funktionen u(x) und v'(x) zerlegt.
In einigen Fällen muss man mehrnmals hintereinend
der partiell integrieren,
ehe man auf ein Grundintegral stö
össt.
∫ u(x)* v '(x) dx
= u( x)* v( x) − ∫ u '( x)* v( x) dx
b
∫ u(x)* v '(x) dx
b
b
a
a
= u( x )* v( x ) − ∫ u '( x )* v( x ) dx
a
v‘ besser zum integrieren.
u besser zum differenzieren.
Bsp.
∫ x * cos(x) *dx
u( x )
= x
v '( x ) = cos( x )
→ Differenziert
→ Integriert
u '( x ) = 1
v( x ) = sin( x )
∫ x * cos(x) *dx = x * sin(x) − ∫ 1 * sin(x)* dx
= x * sin( x) + cos( x ) + C
Achtung: Beim unbestimmteen Integral (keine Grenzen) C nicht vergessen!
Bsp.
π
∫x
2
* cos( x )* dx
0
u( x ) = x 2
v '( x ) = cos( x )
→ Differenziert u'(x) = 2 * x
→ Integriert
π
π
0
0
v(x) = sin( x )
= x 2 * sin( x ) − ∫ 2 * x * sin( x )* dx
u( x ) = 2 * x
v '( x) = sin( x)
→ Differenziert
→ Integriert
π
π

= x 2 * sin( x ) − 2 * x * (− cos( x )) − ∫

0
0
u '( x) = 2
v( x ) = − cos( x )

2 * −(cos( x))* dx

π
= x 2 * sin( x ) − (2 * x * (− cos( x )) − (−2 * sin( x )))
0
0
π
= x 2 * sin( x ) − (2 * x * (− cos( x )) + 2 * sin( x ))
0
= x 2 * sin( x ) + 2 * x * cos( x ) − 2 * sin( x )
π
π
0
π
0
Analysis, Funktionslehre
Partialbruchzerlegung:
Partialbruchzerlegung:
2
1-x 2
1.Polynomdivision, Fal ls Grad des Nenners < als Grad des Zähler
Beispiel:
2.Nenner in faktoren zerlegen und Nullstellen berechnen:
1-x 2 = 0
Nullstellen x = −1
x =1
1-x 2 = −( x − 1)* ( x + 1)
= (1 − x )** (1 + x )
3.Ansatz:
2
A
B
=
+
2
1-x
1− x 1 + x
4.A und B berechnen:
A
B
A * (1 + x ) + B * (1 − x )
2
+
=
=
1− x 1 + x
(1 − x )* (1 + x )
1-x 2
2 ≡ A * (1 + x ) + B * (1 − x )
2 ≡ ( A − B )* x + A + B
A−B = 0
// keine x Anteile
A+B = 2
A=1 B=1
5.A und B einsetzen:
2
1
1
=
+
2
1-x
1− x 1 + x
6.Integrieren mit Ln (Brüche)
Analysis, Funktionslehre
1 − x2
x * ( x − 2) 2
Zähler ist schon faktorisiert
A
1 − x2
B
C
= +
// immer alle n Grade einbeziehen
+
2
x * ( x − 2)
x x − 2 ( x − 2)2
1-x 2 ≡ A * ( x − 2)2 + B * x * ( x − 2) + C * x
1-x 2 ≡ ( A + B )* x 2 + (−4 * A − 2 * B + C)* X + 4 * A
A + B = −1
−4 * A + B + C = 0 // kein x Anteil
4* A = 1
A
( a * x + b )n
oder
A*x + B
( a * x 2 + b * x + c )n
Wenn x2 vorkommt, dann A * x + B
bei (x-1)3
A
A
A
+
+
2
( x − 1) ( x − 1) ( x − 1)3
Nullstellen ermitteln:
3*x 2 * 24 * x + 45
//=0
Nullstellen 5 und 3
= 3 * ( x − 3)* ( x − 5)
TR : factor
irreduzibel:
Wenn es keine Nullstellen hat.
echt gebrochenrational:
Wenn der Grad des Zähler kleiner ist als der Nenner
unecht gebrochen:
Wenn der Grad des Zählers grösser ist als der Nenner
Analysis, Funktionslehre
Schwerpunkt oder „empirischer Mittelwert“:
Wartezeiten, Lebensdauern
f(t) Dichtefunktion
Dichtefunktion f (t ) = λ * e -λ *t
f(t) Dichtefunktion
Messungen, Wägungen
Dichtefunktion =
1
- *( x -µ )2
1
*e 2
2 *π
Mittelwert t ist geometrisch der Schwerpunkt der Fläche des Histogramms.
t = f (t1 ) * ∆ * t1 + f (t2 ) * ∆ * t2 + ....... + f (tn ) * ∆ * tn
f (t1 ) * ∆ = Flächer
t=
t1 = Ort
n
n1
n
* t1 + 2 * t2 + ....... + n * tn
n
n
n
n
t = ∑ ti * f (ti
t in der Mitte der Stabbreite
i =1
t = ∫ t * f (t )dt
Allgemein:
ni
∆t * n
n = Anzahl Messungen, n i = Anzahl Messungen in der Klassennmitte t i
f (ti ) =
∆t = Zeitabstand
Analysis, Funktionslehre
Differenzieren von Hand:
Differnzieren mit trennbaren Veränderlichen:
ist die Gleichu
ung von der Bauart : y ' = g( x )* h( y ) , dann:
Beispiel y ' = −2 * x * y 2 ,
1.Variablen "sortieren":
y ( 0) = 1
|: y 2
y ' = −2 * x * y 2
2.y' selektieren und ersetzen:
y '*
1
= −2 * x
y2
|y ' =
dy
dx
dy=y'*dx
1 dy
*
=−2* x
y 2 dx
1
* dy= − 2 * x * dx
|∫ beidseitiges integrieren
y2
3.beidseitiges Integrieren:
1
∫y
-
2
* dy= ∫ −2 * x * dx
1
= −x 2 + C
y
1
x −C
4.C mit der Anfangsbedingung errechnen
y=
1=
2
1
0 −C
2
|C = -1
allgemeine Lösung: Lösung der Differnzialgleichung ist einee Kurvenschar
 1

y ( x ) = ln * x 2 + C
 2

partikuläre Lösung: Lösung der Differentialgleichung ist eine Funktion
 1
1
y ( x ) = ln * x 2 + 
 2
2
Analysis, Funktionslehre
Lineare Differentialgleichung 1. Ordnung:
ist linear, wenn sie folgende Gestalt hat: y '+ p ( x) * y = q ( x)
p ( x) und q ( x) sind Funktionen, die nur von x aber
nicht von y abhängig sind.
homogene Differentialgleichung, wenn q(xx) = 0
inhomogen, wenn q ( x) ≠ 0.
Beispiel: y '+ tan( x )* y = 2 * sin( x )* cox( x )
1.homogener Teil lösen (alles was von y abhängt )
y '+ tan( x )* y = 0
dy
= − tan( x )* y
dx
1
∫ y * dy = ∫ − tan(x)* dx
− sin( x )
ln y
=∫
* dx
cos( x )
ln y
= ln cos( x ) + C
y
= K * cos( x )
| * dx
:y
| e( )
y ( x ) = K ( x ) * cos( x )
2.Variation der Konstanten:
Ansatz: y = K ( x )* cos( x )
→ Störfunktion
y'= ∫ K ( x )* cos( x ) = K'(x)*cos(x) - K(x)*sin(x)
3.Einsetzen in der Differentialgleichung:
K'(x)*cos(x) - K(x)*ssin(x) + tan(x)*K(x)*cos(x) = 2*sin(x)*cos(x)
y'
y
K'(x)*cos(x) - K(x)*sin(x) + K(x)*sin(x) = 2*sin(x)*cos(x)
K '( x ) = 2 * sin( x )
K ( x ) → integrieren →
∫ 2 * sin(x)
K ( x ) = −2 * cos( x ) + C
y ( x ) = (−2 * cos( x ) + C)* cos( x )
inhomegen : Alles was von y abhängig ist.
Analysis, Funktionslehre
Differentialgleichung der 2. Ordnung:
y ''+ a * y '+ b * y = 0
y ''+ a * y '+ b * y = f ( x )
a,b sin
nd Konstanten
f(x) ist die Störfunktion
homogene Differentialgleichung
inhomogene Differentialgleichung
1. die charakteristiische Gleichung erstellen:
y ''+ a * y '+ b * y = 0
↓
λ 2 + a * λ1 + b * λ 0 = 0
2. mögliche Fälle für die Lösung:
1. y ( x ) = C1 * eλ1 *x + C2 * eλ 2 *x
2. y ( x ) = (C1 * x + C2 ) * e
λ1 , λ 2 zwei reelle Lösungen
λ*x
λ = λ1 = λ 2
eine reelle Doppellösung
3. y ( x ) = er*x * (C1 * cos( w * x ) + C2 sin( w * x ))
λ = r ± i * w zwei konjugiert komplexe Lösungen
konstante Funktion:
y p = c0 Parameter: c0
Polinom , oder lineare Funktion:
y p = c0 + c1 * x + ... + cn * xn
Parameter: c0 ...cn
Trigonometrische Funktion:
g( x ) = A * sin(ω * x )
g( x ) = B * sin(ω * x)
g( x) = A * sin(ω * x ) + y p = B * cos(ω * x )
y p ( x ) = C1 * sin(ω * x ) + C2 * cos(ω * x ) Parameter : C1 , C2
oder C * sin(ω * x + δ )
e-Funktion:
Parameter : C, δ
g(x)=A*eb*x
y p = C * eb* x e
y p = C * eb* x e
Parameter C
Analysis, Funktionslehre
x'' - 4 * x = t3 -1
x(t) = x h (t) + x p (t)
1.homogene Lösung :
x'' - 4 * x = 0
charkteristisch Gleichung :
l1 = 2
l2 - 4 = 0
x h (t) = C1 * e2*t + C2 * e -2*t
l 2 = -2
2.partikuläre Lösung :
Partikuläre Lösung ist immer im Lösungsformel gleicchen Grades (gleicher Form)
wie x p (t) bei x p (x) = sin(x)+ cos(x) dann x p (x) = A * cos(w * x)+ B * sin(w * x)
Ansatz Parametervergleich :
x p (t) = b0 + b1 * t+ b2 * t2 + b3 * t3 =
t3 -1
b0
b1
b2
b3
= -1
=0
=0
=1
y p = a * x3 + b * x2 + c * x + d
y p'' = 6 * a * x + 2 * b
y p' = 3 * a * x 2 + 2 * b * x + c
y p'' - 4 * y p = t3 -1
6 * a * x + 2 * b - 4 *(a * x3 + b * x2 + c * x + d) = t3 - 1
ausmultipliziert :
6 * a * x + 2 * b - 4 * a * x3 - 4 * b * x2 - 4 * c * x - 4 * d = t3 -1
zusammenfassen Parametervergleich :
1
a = - * x3
4
 6 * a - 4 * c = 0 


0
* x2
b
=
 -4 * a = 1 



3
 -4 * b = 0 
c = - *x


8
2 * b - 4 * d = -1
1
d=
4
1 3 3
1
x p (t) = - * x - * x +
4
8
4
1
3
1
x(t) = x h (t) + x p (t) = C1 * e2*t + C2 * e -2*t - * x3 - * x +
4
8
4
Analysis, Funktionslehre
allgemeines:
Allgemeines:
/ e()
2 * x = ln( y )
e
2* x
Allgemein:
e
=y
ey = ex
/ln()
x
y = ln(e + C)
1
ln( y ) = ln( x ) + + C
x
/e()
 1 
 
ex
= y
e
x−y
Wenn Zähler Ableitung vom Nenner:
2*x-1
2
∫ x2 − x + 1 dx = ln(x − x + 1)
1
∫ xdx = ln(x)
y = K * x + e 2 
∫e
n* x
=
1 n* x
*e
n
ln x − ln x + 1 + C2 = ln
2 * ln x = ln x
K '* e−x = e x
K'=e
∫
cot( x ) =
2* x
1
e 2*xdx = * e 2*x + C
2
π
sin   = 1
 2 
cot =
∫
e 2*t
2) =
e ln(
* dt
=5 + C / e( )
2
2 = e5
eln( x ) = x
/ ln
|e( )
1
2
=
Zähler
2*t
e2 = 5
2 = ln(5)
cos( x )
sin( x )
=x*e 2 * eC
1
∫ ln(x)* dx = x * ln(x) − x + C
2
1
ln x + + C
x
∫ −x
cos
sin
x
+ C2
x +1
1
+C
x
∫ Nenner = ln(Nenner ), falls Nenner'=Zähler
4 * ln x 2 − x + 1 + C
2
= (x 2 − x + 1) * K
1
1
−
− * ln x + C = ln x 3 + C
3
1
|e( )
Analysis, Funktionslehre
y‘ und y‘‘:
y ''* cos( x ) + y '* sin( x ) = 0
substituieren :
u = y ' u'=y''
u '* cos( x ) + u * sin( x ) = 0
u ' = −u *
sin( x )
cos( x )
du
dx
sin( x )
du
1*
= −u *
cos( x )
dx
u' =
1
sin( x )
∫ u du = −∫ cos( x) dx
ln u = ln cos( x ) + C
u = K * cos( x )
rücksubstituon :
y ' = K * cos( x )
y = K * sin( x ) + C
Substituieren bei Differentialgleichungen:
y ''+ a * y ' = 0
u = y'
u '+ a * u = 0
du
= −au
dt
∫ u1 * du = ∫ −a * dt
ln u = −a * t + C
u(t ) = K * e−a*t
y (t ) = ∫ u(t ) = ∫ K * e−a*t = −
K −a * t
*e
+ C1
a
Analysis, Funktionslehre
komplexe (imaginäre) Zahlen:
Zeichen
i ei*π = −1
i
−4
i*R
=1
2+2*i
2i
i −3 = i
i
i −2 = − 1
1
i
i
i −1 = 1 = 2 =
= −i
i
i
−1
i0 = 1
x*i
-2
-1
Realzahlen
Pi
-i
1
2
Imaginärzahlen
1
i =i
i 2 = −1
i 3 = −i
i*i
-1
1
x
i4 = 1
i 5 = i ...........-1, -i , 1 , i .........
komplexe Lösungen sind immer konjugiert komplex
TR: complex / cSolve
eine Multiplikation von x mit i bewirkt, eine drehung des Pfeils
von x im Gegenuhrzeigesinn um 90°.
z = x + y * i = Re alteil + Im aginärteil * i
i = −1
i * i = i 2 = −1
z = Gegenzahl zu z = konjugiert komplexe Zahl = x − y * i
2
z = x2 + y 2 = z * z
z = x2 + y 2
z = (1 + ei*t )
e i *π = − 1
konjugiert komplex:
z = (1 + e−i*t )
i 641 = i 640( grösste Zahl durch 4 teilbar) * i = 1*i = i
ei*δ = cos (δ) + i * sin (δ)
ei = 1
R
Analysis, Funktionslehre
Rechenoperationen komplexen Zahlen:
 x
eine komplexe Zahl z = x + y * i ist ein Vektor   in der Gausschen Ebene
y 
Vektor = Zeiger
Menge der kompllexen Zahlen : x = Realanteil von z
y = Imaginäranteil von z (z=y*i ist rein imaginär)
Achtung nur y ist Imaginärteil
z = ist der Betrag einer komplexen Zahl = x 2 + y 2
x1 + y 1 * i = x 2 + y 2 * i
x1 = x 2
y1 = y 2
eine Gleichung liefert also 2 Zahlen
z1 + z 2 = ( x1 + x 2 ) + ( y 1 + y 2 )* i
z1 − z 2 = ( x1 − x 2 ) + ( y 1 − y 2 )** i
z1 + z 2 = z 2 + z1
(z1 + z 2 ) + z 3 = z1 + (z 2 + z 3 )
z + 0 + 0* i = z
−z = (−x ) + (−y )* i
so dass z+(-z)=0
immer z(Zahl) = x(Realteil) + y(Imaginärteil)*i
Multiplikation :
z1 * z 2 = ( x1 + y 1 * i )* ( x 2 + y 2 * i ) =
x1 * x 2 + x1 * y 2 * i + y 1 * x 2 * i + y 1 * y 2 * i 2 = Achtung i 2 wird − 1
( x1 * x 2 − y 1 * y 2 ) + ( x1 * y 2 + y 1 * x 2 )* i
z1 * z 2 = z 2 * z1
( z1 * z 2 )* z 3 = z1 * ( z 2 * z 3 )
z1 * ( z 2 + z 3 ) = z1 * z 2 + z1 * z 3
Analysis, Funktionslehre
z = 2 + 3 * i gesucht z−1 Aufsplittung Realteil Imaginärteil:
 1 
x 2 + 2 * x * y * i − y 2 = −7 + 24 * i
z−1 = 
*
z

 z * z 
x 2 − y 2 = −7
 1 
2 * x * y = 24
z1
 * z 2
= z1 * 
z2
 z 2 * z 2 
Im (x − y * i + 1) + i * Re (−x − y * i + 2) = −0.5 − 6 * i
Bsp.
−y + i * (−x + 2) = −0.5 − 6 * i
13 − 5 * i
1 −0.5
−y =
* (1 + i ) z quer oder z konjugiert
= (13 − 5 * i )*
i )6
(1 −xi )*
+−
1− i
+(21=
= (13 − 5 * i )*
= 9 + 4* i
1
1
1
* (1 + i ) = (13 − 5 * i ) * * (1 + i ) = * (13 + 13 * i − 5 * i + 5)
2
1− i
2
2
z * z = Re(7 )2 + Im( z )2 wird zur reellen Zahl
z + z = 2 * Re( z )
wird zur reellen Zahl
z − z = 2 * Im( z )* i
z1 = z 2 , wenn Re(z1 ) = Re( z 2 ) und Im(z1 ) = Im( z 2 )
Normalform von
(2-3*i)
z
1
1
1
=
* =
*
=
(2+3*i) (2+3*i) z (2+3*i) (2-3*i)
2
3
− *i
13 13
w 2 + w = −3 + 15 * i
Ansatz : w = a + b * i
2
w=?
(a + b * i) + (a + b * i) = −3 + 15 * i
i =?
Ansatz : w = i
2
(a + b * i) = i
w2 = i
Division mit komplexen Zahlen:
_
-z
R*i
Kartesische Form oder Normalform:
z = x+y*i
Trigometrische Form:
z = r * (cos ϕ + i * sin ϕ )
+ Exponentialform oder Polarform:
z
sin(φ)
r
+φ
cos(φ)
-φ
r
r
R
_
z
-z
r = Radius = Zeiger
Analysis, Funktionslehre
z = r * e i*ϕ
-
ϕ heisst Argument von z, kurz arg(z)
Argument Bereich -π bis π
r ist der Radius von z , r= z
Umrechnung:
z = x+y*i
r=
2
x +y
,x ≠ 0
2
 y 
 x 
und ϕ = arctan 
sofern x>0
 y 
 x  + π sofern x<0
ϕ = arcctan 
ist x=0 und y<0
ϕ=−
2
so gilt x = r * cos( ϕ ) und y = r * sin( ϕ )
Multipikation, Division bei trigonometrischen Form:
z 1 * z 2 = r1 * r2 * (cos( ϕ 1 + ϕ 2 ) + i * sin( ϕ 1 + ϕ 2 ))
z1
z2
=
r1
r2
r = x2 + y 2
arctanϕ =
wenn x < 0
Arctan:
2
1. und 2. Quadrant positiv + z = r * eϕ*i
π 3. und 4. Quadrant negativ -
ϕ=
ist z = r * e
Kartesisch → trig. Form
z = x+i*y
* (cos( ϕ 1 − ϕ 2 ) + i * sin( ϕ 1 − ϕ 2 ))
trig. Form → Kartesisch
Umgekehrt:
y = r * sin(ϕ )
z = r * cos( ϕ )
z = z +y*i
Multipikation, Division bei Exponentialform:
z 1 * z 2 = r1 * r2 * e
z1
z2
=
r1
r2
*e
y
(+π)
x
π
ist x=0 und y>0
i*ϕ
(Modulo π)
i *( ϕ 1 + ϕ 2 )
i *( ϕ 1 − ϕ 2 )
Bei der Multiplikation werden Radien multipliziert, Argumente addiert.
Bei der Diviision werden Radien dividiert, Argumente subtrahiert.
Analysis, Funktionslehre
Potenzen:
= r * e i*ϕ
z
z n = r n * e i *n * ϕ
bei kartesicher Form:


y
→ r und ϕ ausrechnen  r = x 2 + y 2 , ϕ = arctan   (bei x < 0 -180°)
 x 


→ z = e x*π*i
→ z n = e x*π*n*i
→ in kartesische Form zurück (y = r * sin(ϕ )
x = r * cos(ϕ ))
n-te Wurzel:
zn = a
n=?
r * (cos(δ ) + i * sin(δ )) = a 0 * (cos(α ) + i * sin(α ))
n
r n = a0
δ=
x
r = n a0
α +k * 2*π
n
r *e
k ∈
(0,1,2,3,4......)
α +k * 2*π
n
Bsp: z = 4 − 2 * i = r * ei*ϕ
z2 = 4 − 2 * i
r = 4 20
= r 2 * ei*2*ϕ
= 20 * ei*α
 −2 
α = arctan  
 4 
ϕ1 =
2* ϕ = α +k * 2*π
ϕ2 =
α +1* 2 * π
2
z = 4 20 * eϕ*i
α + 0* 2*π
2
α + 2*π
ϕ2 =
2
ϕ1 =
ϕ1 =
α
2
Für n-te Wurzel gibt es n Lösungen!!!!
Analysis, Funktionslehre
Einheitskreise mit z = r * ei*ϕ :
π
i*
z =r =1
e 2
i
Allgemein:

n
n
z = r *e

i*δ+k *2*π
n



0 ≤ k ≤ (n-1)
n*i
z2
z1
-Re
ei*π
−1
φ
-φ
-φ
+Re
-i*
e
-i
z3
z4
-n*i
beim Einheitskreis:
Radius=1
 π + k *π *i


2 
eo etris
e
r 3 δ=
eutu
ung au
r 3 * ei*δ* 3 = 5 * ei*arctan( 0.5 )+k *2*π*i
k * 2*π
1
3 * δ = arctan(0.5) + k * 2 * π = * arctan(0.5) +
3
3
 1
k * 2*π 
 *arctan( 0.5 ) +
* i
3 
1
 1 *arctan( 0.5 ) + k * 2*π * i


3 
z k = 5 6 * e 3
π
π
+k *
4
2
k 0 1 2 3
reis
2 + i = 5 * ei*arctan( 0.5 )
3 * δ = 5 6 * e 3
π
2
Faktorisierung & Nullstellen :
z3 = 1
z3 −1 = 0
3
1
*i
z =− ±
2
2

 1
 1
3  
3   

z 3 − 1 = (z − 1) * z − − +
* i   * z − − −
* i  

2
2
  
 
 2
 2
z = 3 * e 4
z3 = 2 + i
z = r * e i *δ
z 3 = r 3 * e i *δ * 3
__
z1
e0*i
1
e i * π = −1
z = r * e i *δ
z 4 = −81
r 4 * e4*i*δ = 81 * ei*π+k * 2*π*i
r 4 = 81
4* i *δ = i *π +k * 2*π
1
z1
+φ
0≤k ≤2
Analysis, Funktionslehre
z = ei*t = cos( t ) + i * sin(t )
z = e−i*t = cos( t ) − i * sin(t )
ei*t + e−i*t = 2 * cos( t )
ei*t + e−i*t
cos( t ) =
= cosh(i * t )
2
ei*t − e−i*t = 2 * i * sin(t )
ei*t − e−i*t 1
sin(t ) =
= * sinh(i * t )
2* i
2
e z + e−z
2
e z − e−z
sinh( z ) =
2
ei*z = cos( z ) + i * sin( z )
cosh( z ) =
z
z
e = e *e
i* y
e z1 * e z 2 = e z1 + z 2
ei*z + e−i*z
2
i* z
e − e−i*z
sin( z ) =
2* i
sin( z )
tan( z ) =
cos( z )
cos( z )
cot( z ) =
sin( z )
cos( z ) =
cos( z ) = cosh(i * z )
1
sin( z ) = sinh(i * z )
2
cos( z ) 2 + sin( z ) 2 = 1
3
16
(1 − 2 * i) = 5 * ei*arctan(-2)*16 = 58 * ei*arctan(-2)*16
1
(−1 + i)2 → substituiere → ω 2 = (−1 + i)
3
i * * π + k * 2* π * i
4
ei*t + e 2*i*t = cos(t ) + cos( 2 * t ) + i * (sin(t ) + sin( 2 * t ))
2−i = e−i*ln( 2 )
→
e−y = 7
e−b = 2
-b = ln( 2)
/ ln
ex = ey * ez =
x = y+z
ln(−3) = ln(−1) + ln( 3)
w = ln(−1)
e w = −1
w = (π + k * 2 * π) * i
bei :
2
(z + i) = 2 * i
(z − 2 * z ) = 1
Klammer Substituieren
−1 − i
−2
∞
y = − ln (7)
− sinh(i * t )
i * sin(t )
=
1 + cosh(i * t ) 1 + cos(t )
Punkt z wandert aud der Parabel
y = x2
z = x +i* y
also : z = x + i * y
(z + 1) = 2 → substituiere → ω 3 = 2
r 2 * e i * 2* ϕ = 4 2 * e
3
ϕk = π + k * π
8
i*t
−i * t
1 − ei*t (1 − e ) * (1 + e )
=
=
1 + ei*t (1 + ei*t ) * (1 + e−i*t )
y=x2
z −4 = − 2
r 4 * e−i*4*π = 2 * ei*π+ 2*k *π
−π
π
+k *
ϕ=
k = 0, .., 3
4
2
16
e z1
= e z 1 −z 2
z2
e
1
e−z = z
e
z
e ≠ 0 für jedes z
→ *(−1)
∑n*e
n=0
−n * i
* zn
→
→
1+ i
2
an = n * e−n*i
Analysis, Funktionslehre
TI 89:
Winkel vom Zeiger -> angle
für imaginäres Gleichungssystem -> complex / cSolve
MODE ->Complex Format
->POLAR
->RECTANGULAR (oder REAL)
->RECT (Kartesisches Format)
Funktionen:
MODE -> GRAPH -> PARAMETRIC
HOME: Funktion abspeichern f(t) ->STO Achtung: immer t verwenden als Unbekannte!!!
|z-2|=1
xt1=real(f(t))
|(x+i*y)-2|=1
yt1=imag(f(t))
Kreis mit R=1 mit Mittelpunkt bei Re(2)
F2=Zoom ->ZoomFit
π
Im
f  
y
 4 
π
f (t ) = 2 + i + 3 * ei*t mit t ≥
4
�
4
i
cos(b * y ) + i * sin(b * y ) =
2
y
Konvergenzradien :
∞
f (z) = ∑
k
(z − i)
k
Konvergenzradius r::
k =0
k
=1
r →∞ k + 1
r = lim
Re
e i *b * y
Achtung: imaginäre e Funktionen
sind periodisch!
Für welche z ∈ konvergiert die Reihe:
n
i*z
∞
∞  i*z 
e i *n * z
 e  q = e
=
q <1
∑
∑

n


3
3
n=0
n=0  3 
Für welche z konvergiert die Reihe aus (a) gegen
1+ i :
1
1
= 1+ i
=
 ei*z 
1−q


1 − 
 3 
Konvergenzradius ist der Radius (r = 1) eines Kreises
Innerhalb dieses Kreises konvergiert die Reihe.
Analysis, Funktionslehre
Integration und Ableiten von komplexen Zahlen:
-trennen von Realteil und Imaginärteil
-i als Konstante aussserhalb der Integration
b
b
b
a
a
a
∫ f (t )dt = ∫ u(t )dt + i * ∫ v(t )dt
Realteil
∫
ep*t dt
Imaginärtei
p ist eine imaginäre Zahl
= ∫ e x*t * ei*t*y dt
=∫ e
x*t
* cos(ty ) + e
x*t
* sin((ty )* i
Die Ableitung von f (t ) ist:
f '(t ) = x '(t ) + i * y '(t )
Die Integration von f (t ) ist:
∫ f(t) = ∫ x(t ) + i * ∫ y(t )
Re alteil ,
Imaginärteil
Integrations und Ableitungsregeln
sind gleich wie beiim herkömmlichen
Zahlenraum!!!!
Falls ein Gebiet G ⊆ gibt, das [a,b] enthält und falls f auf G eine
Stammfunktion F hat:
b
∫ f (t )dt = F(b) − F(a)
F ist Stammfunktion
a
f ( z ) = ep*z ist definiert auf dem Gebiet G und hat dort Stammfunktion:
F( z ) =
1
1 p* z
*e
p
1
∫ (t + i )dt = ∫ (t + i )dt
0
→ nur die Ortskurve
0
Für eine Funktion nennt man jede Lösung z der Gleichung f ( z ) = z
einen Fixpunkt
f (z ) = a * z + b z = ?
−b
z=
a −1
Fixpunkt = 1 a * 1 + b = 1
bildet z = 1 + i auf ω = -2 ab a * (1 + i ) + b = −2
Analysis, Funktionslehre
Wurzelortskurve:
Wurzelortskurve:
Da man die Nullstellen eines komplexen Polynoms auch „Wurzel“ nennet, heisst
die Kurve, welche duch Aufzeichnung aller Nullstellen entsteht Wurzelortskurve.
Dabei durchläuft ein Parameter k meistens alle reellen Zahlen.
1
Wertebereich von − * 1 ± 1 − 2 * k :
2
zwei Parabeläste Wertebere ich = (
Beispiel :
P ( z ) = z 2 + z + 0 .5 * k
k =Nullstellen von P(z)
ngsformel
Ansatz: Lösun
z1, 2
-b ± b 2 − 4 * a * c
2*a
−1 ± 1 − 2 * k
=
2
1- 2 * k ≥ 0
reell für
k≤
komplex für 1 - 2 * k < 0 k >
z1, 2
1
2
(
(
z1,2(k)
0.5
1
2
1
1
− * 1 ± 1− 2 * k ,
k≤
2
= 2
1
1
− * 1 ± 2 * k −1 * i ,
k>
2
2
)
k
)
)
1
Wertebereich von − * 1 ± 2 * k −1 * i :
2
1
Alle z1,2 haben den Realteil −
2
Wertebereich von ± 2 * k −1 ist (
)
zeichnen der Wurzelortskurve TI89:
∞*i
-∞
-0.5
1 − 2 * k = 2 * k −1 * i
+∞
-∞*i
Achtung i nicht im Taschenrechner
beim Imaginärteil eingeben!!!!
-Mode->Graph->Parametic
-A
Als Variable t verwenden!!!
 1
-x1 Realteil von z1 − 
 2 
 1

-y 2 positive Wurzel von z 1  − k 

 2
 1
-x 2 Realteil von z 2 − 
 2 

1 
-y 2 negative Wurzel von z 2 − k − 
2 

-Step , min , max von t einstellen
Analysis, Funktionslehre
komplexe Funktionen und Ortskurven:
f : →
Input ist eine reelle Zahl, Output ist komplex
f (t ) = t + i * t 2
i*R
 t   Re 
r(t ) =  2   
 t   Im 
   
„Ortskurve“ von f(t)
Ortskurve ist keine
Funktion sondern nur
der Output!
r(t)
R
i*R
f (t ) = t * ei*t Kreis mit r = t auf Einheitskreis
 t * cos(t )  Re 
  
r(t ) = 

  
 t * sin(t )   Im 
R
„Ortskurve“ von f(t)
f:
→
Bilden komplexe Zahlen auf komplexen Zahlen ab.
1
Die Inversion: f ( z ) =
z
Die Zahlen ausserhalb des Einheitskreie werden in den Einheitskreis
abgebildet.
Die Zahlen in
nnerhalb des Einheitskreises werden auf Zahlen ausserhalb
des Einheitskreises abgebildet.
i*R
Bei Beträgen:
z − z0 = k
Mittelpunkt = z 0
Radius = k
R
z0
z
Einheitskreis
z
M
φ
-φ
„Ortskurve“ von f(z)
φ
-φ
R
f(z) ≤ Einheitskreis
f(z) ≥ Einheitskreis
Analysis, Funktionslehre
spezielle Formen von Ortskurven:
Fixpunkte :
z heissen Fixpunkte einer Funktion f(z), wenn
z = f (z )
1
f (z ) =
1- z
1
→
z = f (z )
z=
1- z
→ Lösungssformel
z2 − z + 1 = 0
Gerade horizontal:
f (t ) = 2 + t * i
Gerade vertikal:
f (t ) = t + 5 * i
Teil einer Geraden:
1
f ( t ) = −1 + * i
t>0
7
Kreise mit Mittelpunkt bei 0 und r = 3 :
1
3
z 1, 2 = ±
*i
f (t ) = 3 * ei*t
0 ≤ t < 2*π
2
2
Kreis mit Mittelpunkt bei (4, 5*i) und r = 2 :
f ( t ) = 4 + 5 * i + 2 * ei*t 0 ≤ t < 2 * π
Halbkreis mit Mittelpunkt bei 0 und r = 7 :
0≤t <π
f (t ) = 7 * ei*t
i*R
Fusspunkt
P
r
1/g
Einheitskreis
R
Q
g
1/r
grösster Re Wert der Inversion von g
ist Q, weil P der klein
nste Abstand zu 0
1
wenn P am kleinsten, nimmt Q den grösssten
P
Realen Wert an.
Gerade unter Inversion ergibt immer einen Kreis!
g ergibt k
Analysis, Funktionslehre
Geometrische Reihen:
Eine geometrische Reihe ist eine (unendliche) Zahlenfolge
deer Gestalt:
s1 = a, s 2 = a + a * q, s 3 = a + a * q + a * q 2 , ....,
sn = a + a * q + a * q 2 + .... + a * qn−1
sn heisst die n-te Partialsumme
Grundform
∞
a
k -1
*
a
q
=
∑
1− q
k =1
1 − qn
, sofern q ≠ 1
sn = a *
1− q
a
lim sn =
, für q <1 = a + a * q + a * q 2 + a * q 3 .....
n→∞
1− q
E(Fehler) =
a
− sn ( Partialsumme)
1−q
=
a
1 − qn
−a *
1−q
1−q
=
a
n
*q
1−q
En ( Wert ) =
q <1
(für q < 1)
a
n
* q * ( Wert )
1 − q( Wert )
q =zweite Partialsumme durch erste Partialsumme
Grundform der geometrichen Reihe:
a = 30
q = 0, 7
∞
∑ 30 * 0, 7
k −1
k =1
a = 2 , Re ihe = 2 2*q = −
3
2
3
q=?
2
Bsp :
k −1
 1 
− 
∑
 8 
k =1 
1
8
16
8 16 32
8
+ + + ... a= , q = 9
8
3 9 27
3
3
23
1
0, 2323232323 a=
,q =
100
100
∞
a = 1, q = −
Analysis, Funktionslehre
Funktionsreihe:
Eine Funktionsreihe ist eine (unendliche) Zahlenfolge der Gestalt:
s1(x)=u1(x)
∞
s2(x)=u1(x)+u2(x)
uk ( x)
∑
s3(x)=u1(x)+u2(x)+u3(x)
k =0
sn(x)=u1(x)+u2(x)+u3(x)+...+un(x)
sn(x) heisst n-te partialsumme ans der Stelle x.
Funktionsreihen:
für den Grenzwert, falls er existiert f(x)
∞
k −1
f ( x ) = ∑ (cos( x ))
k =1
a =1
q=x
ε15 an der Stelle x = 3
ε15 =
1
a
n
15
*q =
* cos( 3)
1− q
1 − cos( 3)
Welchen Fehler En(x) macht man, wenn man an der Stelle x den Grenzwert der
Reihe annähert durch die n-te Partialsumme?
Existiert der Grenzwert f(x) einer Funktionsreihe in einem ganzen Bereich D der
reellen Zahlen, so heisst f Grenzfunktion. Die Reihe heisst konvergent an der stelle
x für jedes x Element von D.
x statt q
Grenzwert f ( x)
Konvergenz bei Geometrischen Reihen:
1 + (q)
a =1
q = ()
1 = ()
−1 = ()
q <1
Konvergenzradius :
∞
n
(−1)n * n * x 2*n
∑
2
n=0
substitution x 2*n = x 2 = t
(−1)n * n
(−1)n +1 * n + 1
a
ak =
=
k +1
2n
2n +1
n
n +1
a
2*n
(−1) * n * 2
=
=
lim k = n
n +1
n →∞ a
2 * (−1) * n + 1
(n + 1)
k+1
n
n
1
2*
= 2* n = 2*
=2
n 1
1
n +1
1+
+
n n
n
Rücksubstitution :
− 2 <x< 2
Analysis, Funktionslehre
y
Potenzreihen:
Divergenzbereich
Konvergenzbereich
x0-r
Divergenzbereich
x0+r
x0
z
Eine Funktionsreihe der Gestalt:
∞
∑a
k =0
k
* ( x − x 0 )k heisst Potenzreihe.
a 0 , a1 , ... heissen Koeffizienten der Potenzreihe
x 0 heisst Entwicklungspunkt
r(Konvergenzradius ) = lim
n→∞
an
an+1
∞
ist r der Konvergenzradius der Potenzreihe ∑ ak * ( x − x 0 )k
k=0
so konvergiert die Potenzreihe für jeden Wert x miit x − x 0 < r und sie
divergiert für alle x-Werte mit x − x 0 > r
x 0 bei minus +, bei + minus
an+1 muss überall wo n vorkommt +1 gerechnet werden
Grundform der Potenzreihe:
Bsp :
( x − 2 )k
∑
k
k =1
∞
1
x 0 = 2, ak =
k
f k −teAbleitung ( x 0 )
k!
1
1
an =
an+1 =
n
n +1
an =
a
r = lim n = lim
n→∞ a
n→∞
n +1
∞
∑a
K =0
k
* ( x − x 0 )k
Beim Konvergenzradius Reihe
in diese Form bringen.
Bei Brüchen:
101 ∞
0.101 = 3 * ∑ 10−3*k
10 k =0
1
n = lim 1 + 1 = 1 Achtung bei Konvergenzradius:
r=1
n→∞
1
n
-1 ≤ (x − 3)(durch substitution) ≤ 1
n +1
2≤x≤4
Analysis, Funktionslehre
∞
x 2*k
k =1
3k * (k + 1)* k + 1
∑ (−1)k *
substituier u = x 2
∞
neue Reihe:∑ (−1) *
uk
k
k =1
3k * (k + 1)* k + 1
- 3 <x< 3
−−−−−−−−− − −−−−−−−−−−−−−−−−−−−−−

x 5*k +1 x 6
x11
x16
x5
x10 
6 1

x
...
*
+
+
=
+
+
=

 3 1 + 4 1 + 8 
1 + 2k
3 1+ 4 1+ 8
Re sultat : u < 3
u = x5
neue Reihe :
1
u
u2
...
+
+
1+ 2 1+ 4 1+ 8
ak =
1
1 + 2k
−2 ≤ x 5 ≤ 2
−5 2 ≤ x ≤ 5 2
f (k) *(x0 )
*(x - x0 )k
k!
k=0
n
Tn (x) = ∑
¥
ex = ∑
k=0
1
* xk
k!
für jedes x ∈ R
(-1)k
* x2*k
k=0 (2 * k)!
¥
cos(x) = ∑
(-1)k * x k+1
ln(1 + x) = ∑
k +1
k=0
¥
für jedes x ∈ R
für x < 1
für jedes x ∈ R
(-1)k
* x2*k+1 für x < 1
k=0 (2 * k + 1)
¥
arctan(x) = ∑
¥
1
= ∑ xk
1 - x k=0
∞
irgendwas + ∑ Term
k=1
(-1)k
* x2*k+1
(2
*
k
+
1)!
k=0
¥
sin(x) = ∑
Achtung:
Es ist legitim, falls k erst
von der 2. Partialsummee
passt:
ak
für x ∈ (-1,1)
Analysis, Funktionslehre
Man bestimme die Anzahl der Summmanden, die nötig sind,
(x-2)k
im Intervall (1.5, 2.5) auf
∑
k
k=1
zwei Nachkommastellen genau zu approximieren (0,,01).
um die Grenzfunktion f(x) von
∞
∞
(x-2)k N−1 (x-2)k
(x-2)k
N-te
Partialsumme
=
+
(
)
(Rest R N )
∑
∑
∑
k
k
k
k=1
k=N
k=1
Gesucht N, Rest R N so, dassR N < ε = 0.001 bim Intervall(a,b)=(1.5 , 2.5)
∞
bk =
( x − 2 )k
k
bk +1 =
( x − 2)k +1
k
= k + 1k =
* ( x − 2)
( x − 2)
k +1
k
bk+1
bk
k
* ( x − 2)* bk
k +1
k
<1, (x-2) <0.5
k +1
bk+1 ≤ 0..5 * bk
bei Höchstwerten! für x ∈ [1.5, 2.5 ]
bk+3 ≤ 0.5 * bk +2 ≤ 0.53 * bk
bk+j ≤ 0.5 j * bk
∞
∞
∑ bk ≤ ∑ bk
RN =
k =N
k =N
∞
∞
= ∑ b N+ j ≤ ∑ 0.5 j * bn
j=0
j=0
∞
= bn * ∑ 0.5 j
(genaue Reihe)
j=0
= bn *
1
= bn * 2
1 − 0.5
R N ≤ bn * 2 = 2 *
2*
N
0.5
= 0.01
N
x−2
N
N
0.5N
≤ 2*
<ε
N
N=5.25
Analysis, Funktionslehre
Grundform geometrischen Reihe:
∞
∑a*q
k
k =0
Grundform Potenzreihe:
∞
∑a
k =0
k
* ( x − x 0 )k
x 2 ist Enwicklungspunkt
a 0 , a1 ....an sind Koeffizienten
Grundform Funktionsreihe:
∞
∑a*x
k
q ist variabel =x
k =0
∫
x
∞
sin( x )
(−1)k
* dx = ∑
* ∫ x 2 k dx =
x
k =0 ( 2 * k + 1)!
a
(−1)k
(−1)k
x 2*k +1 x ∞
a 2*k +1 x
*
¦=
*
¦
−
∑
∑
k =0 ( 2 * k + 1)! 2 * k + 1 a
k =0 ( 2 * k + 1)! 2 * k + 1 a
∞
(−1)k
x 2*k +1 x
*
¦+ C
∑
k =0 ( 2 * k + 1)! 2 * k + 1 a
∞
1 − cos( x )
x →∞ x * sin( x )
lim
( 2 * x ) 2 ( 2 * x )4
+
− ....
2!
4!
( 2 * x ) 2 ( 2 * x )4
1 − cos( 2 * x ) =
−
+ ....
2!
4!
x4 x
x * sin( x ) = x 2 − + ....
!
!
2
(2 * x )
( 2 * x )4
−
+ ....
2 − ....
1 − cos( x )
4!
= 2!!
=
=2
lim
4
x →∞ x * sin( x )
x
x
1 − ....
2
x − + ...
!
!
cos( 2 * x ) = 1 −
Analysis, Funktionslehre
Man bestimme die Anzahl der Summanden, die nötig sind,
um diie Grenzfunktion f(x) von ln(1+x) im Intervall(-0.5, 0.5) auf
<10-5 genau zu approximieren.
n−1
ln(1+x)= ∑
k=0
bk =
x
(−1)k k+1
*x
∑
k=n k+1
∞
(<10 )
-5
k +1
k +1
bk +1 =
b k +2
(−1)k k+1
*x
+
k+1
x
k +2
x
=
k +1
*x
k +1
≤ bk * x
k +2
≤ 0.5 * bk
k +2
k +1
≤ bk +1 * 0.5 ≤ bk * 0.52
bk + j ≤ bn * 0, 5 j
∞
(−1)k k+1
≤
bn
*
0, 5 j = bn * 2
*x
∑
∑
k+1
j=0
k=n
∞
2=
a
1− q
2 * bn ≤ 10−5
0, 5n+1
2*
≤ 10−5
n +1
-------- ertetab elle erstellen
∞

∞
sin2*k (t )* dt = ∫  ∑ sin
∑
∫

k =0
k =0
2* k

(t ) * dt

∑ und ∫ vertauschen immer gestattet!
x
∞ 1
k
* (−t 2 ) dt
∫ ∑

k =0 k !
0
= Potenzreihen dürfen Summaandenweise integriert werden.
x
1
* (−1)k * ∫ t 2*k * dt
∑
k =0 k !
0
∞
Analysis, Funktionslehre
Fourier-Reihen:
∞
∑a
k=0
k
* ( x − x 0 )k im Konvergenzintervall (x 0 − r , x 0 + r )
In der Naähe des Entwicklungspunktes kann f(x) schon durch
eien Parrtialsumme mit wenigen Summanden gut angenähert werden.
Inn
nerhalb eines vorgegeben Intervalls soll die Näherungsfunk
ktion
die gegebene Funktion f(x) überall ungefähr gleich gu
ut approximiert
sein.
Das Mass für eine gute Approximation f(x) und g(x) ist das
Abstandsquadrat:
Unter dem Abstandsqu
uadrat zweier Funktionen f(x) und g(x),
welche im Intervalll (a, b) definiert sind, verstehen wir das Integral:
b
2
∫ (f (x)−gg(x))
* dx
a
f ( x ) und g( x ) heissen orthogonal, wenn ihr Skalarprodukt
Nulll ergibt.
Auf dem Intervall (0,T) mit ω =
1,cos(ω * t ),cos( 2 * ω * t ), ......
sin(ω * t ),sin( 2 * ω * t ), .........
2* π
paarweise orthogonal:
T
Eine Funktion g aus V ist zerlegbar nach f i i = 1, 2, 3, 4........
wenn gilt:
∞
g=∑
i =1
(g, fi )
* fi
(f i , f i )
Analysis, Funktionslehre
Ein Vektorraum sit eine Menge V on Elementen, die man zuein
nender
addieren und die man mit einer Zahl multiplizieren kann.
x,y,z ∈ des Vektorrames
a,b
reelle Zahlen
1. ( x + y ) + z = x + ( y + z )
2. x + y = y + x
3. Element 0 in V, so dass gilt x + 0 = x
4. Element - x in V, so dass gilt x + (-x ) = 0
5. a * (b * x ) = (a * b )* x
6. 1 * x = x
7. a * ( x + y ) = a * x + a * y
8. (a + b )* x = a * x + b * x
Skalarprodukt zweier Funktionen:
b
(f1 , f 2 ) = ∫ f1 ( x )* f 2 ( x )* dx
a
(f1 , f 2 ) = (f 2 , f1 )
(f1 + f 2 , f 3 ) = (f1 , f 3 ) + (f 2 , f 3 )
(a * f1 , f 2 ) = a * (f1 , f 2 )
Analysis, Funktionslehre
Die Reihe heisst trigonometrische Reihe:
∞
a0
+ ∑ ak * cos(k * ω * t ) + bk * sin(k * ω * t )
2 k =1
2* π
heissen reelle FourierT
koeffizienten ak und bk sind Koiffizienten der Fourierreihe:
für eine Funktion f (t ) mit der periode T und ω =
T
2
ak = * ∫ f (t )* cos(k * ω * t )* dt
T 0
k ≥0
T
2
bk = * ∫ f (t )* sin(k * ω * t )* dt
T 0
k ≥1
T
2
a 0 = * ∫ f (t )* dt
T 0
Fourierreihe:
Sf (t ) =
∞
a0
+ ∑ ak * cos(k * ω * t ) + bk * sin(k * ω * t )
2 k =1
Integralform ausgedrückt duchrch Summe:
b
∫ f (t) * dt
a
n−1
≈ ∑ f (t k ) * ∆t
k =0
komplexe Fourrier ausgedrückt duch Summe:
1 T
i*k*ω*t * dt
* ∫ f (t) * e−
T 0
−i*k*ω*tk
* ∆t
≈ ∑ f (t k ) * e
Analysis, Funktionslehre
Dirichelet - Bedingung:
Ist eine T-periodische Funktion f ( t ) auf dem Intervall [0, T ] stückweise
stetig differenzierbar, so gilt für die Fourier-Reihe S f ( t ) :
-ist f auf dem Teilintervall [a,b] stetig, so konvergiert die S f
auf [a, b] gegen f.
-ist t 0 eine Sprungstelle von f, so gilt:
Sf (t 0 ) =
1
2
(
)
* lim f ( t ) + lim f ( t )
f →t0
+
f →t0
−
das heisst, S f ( t 0 ) ist in
n der Mitte der Sprungstellen
Symmetrie:
Für die Berechnung der Fourier-Koeffizienten gilt:
-anstelle der Periode [0,T
T] kann [a,a+T] als Intervall verwendet werden
-für Funktioonen f ( t ) = -f (−t ) gilt
ak = 0
-für Funktionen f ( t ) = f (−t )
bk = 0
gilt
y
-t
-t
t
0
t
Analysis, Funktionslehre
Komplexe Fourier Darstellung :
1
* (e i*x + e -i*x )
2
1
* (e i*x + e -i*x )
sin(x) =
2*i
∞


a
1
1
* (e i*k*w*t + e -i*k*w*t )
Sf (t) = 0 + ∑ a k * * (e i*k*w*t + e -i*k*w*t ) + b k *


2*i
2
2
k=1 
cos(x) =

 n
i*k*w*t
 c * e i*k*w*t  =
=
lim
c
*
e
∑
∑
k
k

n →∞ 
n=-n
k=- ∞
∞

 n
a0
+ lim ∑ (a k * cos(k * w * t)+ b k * sin(k * w * t))

2 n→∞  n=1
a0
2
1
c k = *(a k - i * b k )
2
1
c -k = c k = * (a k + i * b k )
2
c0 =
T
1
Die Zahlen c k = * ∫ f(t)* e i*k*w*t * dt
T 0
mit k ∈ Z heissen
komplexe Fourierkoiffizienten von f(t)
Die komplexe Fourierreihe :
a0 ∞
* ∑ ck * ei*k*w*t
2 k=-∞
Integralbildung :
t 2 =T

 t1
1 
−i *k * ω* t
ck = *  ∫ f (t )* e
* dt + ∫ f (t )* e−i*k *ω*t * dt 

T  t
t1
0
t0
t1
t2=T