Testen von Hypothesen bei gesuchtem

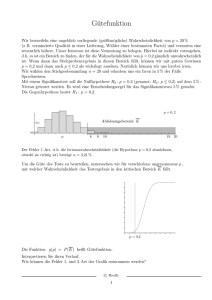
Mathias Russ, MK 19.04.2007 Hypothesentest_Ueb_Alpha.mcd
Testen von Hypothesen bei gesuchtem Annahmebereich - Übungen
(7) Wieder der Schulschwänzer
Von einem Schüler wird behauptet, dass er (mindestens) 40% der Unterrichtstage schwänzt (Nullhypothese).
Um diese Vermutung zu bestätigen, werden 20 zufällig ausgewählte Tage überprüft. Die Nullhypothese wird
angenommen, wenn mindestens 8 Fehltage dabei sind.

Der Ablehnungsbereich A = 0 .. 7 liefert einen Fehler 1. Art von 41,589%.
Finden Sie den größtmöglichen Ablehnungsbereich, für den α höchstens 5% beträgt.
(8) Noch einmal Lerneifer
Einem Schüler werden in einer Prüfung 25 Fragen gestellt, die er mit „ja“ oder „nein“ beantworten kann und soll.
Der Prüfer vermutet, dass der Schüler nicht vorbereitet ist und somit rät (Nullhypothese).
Ermitteln Sie den größtmöglichen Ablehnungsbereich, wenn die Wahrscheinlichkeit den Schüler zu Unrecht als
Lerner einzuschätzen kleiner als 1% sein soll.
(9) Wahltag
Bei der letzten Wahl hat ein Kandidat 35% der Stimmen erhalten. Vor der kommenden Wahl wird eine Umfrage
durchgeführt, um zu ermitteln, ob dieser Kandidat dieses Mal mindestens genau so gut abschneidet
(Nullhypothese). Von 200 befragten Wählern seines Wahlkreises sagen 64, dass sie ihn wählen werden.
a) Bestimmen Sie den größtmöglichen Ablehnungsbereich der Nullhypothese für das Signifikanzniveau 5%.
Zu welcher Entscheidung kommt man durch das Testergebnis?
b) Beschreiben Sie, worin bei diesem Beispiel der Fehler 2. Art besteht.
(10) Call-Center
Ein Call-Center möchte seine Kundenfreundlichkeit verbessern. Nach Einbau einer neuen Telefonanlage und
Schulungen aller Mitarbeiter werden 200 zufällig ausgewählte Kunden nach Ihrer Zufriedenheit befragt. 130
Kunden waren mit dem Gebotenen zufrieden. Bisher waren 30% der Kunden unzufrieden mit dem Service.
Ein Mitarbeiter äußert die ketzerische Vermutung, dass sich nichts geändert hat.
Geben Sie die Testgröße T und die Nullhypothese H0 an. Bestimmen Sie den größtmöglichen
Ablehnungsbereich der Nullhypothese auf dem 5%-Niveau.
Stimmen Sie aufgrund dieses Tests unserem Ketzer zu?
(7) Wieder der Schulschwänzer
Von einem Schüler wird behauptet, dass er (mindestens) 40% der Unterrichtstage schwänzt (Nullhypothese).
Um diese Vermutung zu bestätigen, werden 20 zufällig ausgewählte Tage überprüft. Die Nullhypothese wird
angenommen, wenn mindestens 8 Fehltage dabei sind.

Der Ablehnungsbereich A = 0 .. 7 liefert einen Fehler 1. Art von 41,589%.
Finden Sie den größtmöglichen Ablehnungsbereich, für den α höchstens 5% beträgt.
Nullhypothese H0: Der Schüler fehlt mindestens an 40% der Schultage
Testgröße: Anzahl der Fehltage
Stichprobenlänge n = 20
Signifikanzniveau α ≤ 5%
Gesucht: Entscheidungsregel (linksseitiger Test)
H0 p0 ≥ 0.4
Annahmebereich A = c + 1 .. 20

Ablehungsbereich A = 0 .. c
Annahme von H0 , richtige Entscheidung
falsche Entscheidung, Fehler 1. Art, α
Tafelwerk, S. 21
T
SPBinTabelle ( 20 , 0.4)
=
0
0
3.65616·10 -5
1
2
3
4
0.00052
0.00361
0.01596
0.05095
α = 0.05095 > 5%
α = 0.01596 < 5%

Der Ablehnungsbereich A = 0 .. 3 liefert einen Fehler 1. Art von 1,5%
(8) Noch einmal Lerneifer
Einem Schüler werden in einer Prüfung 25 Fragen gestellt, die er mit „ja“ oder „nein“ beantworten kann und soll.
Der Prüfer vermutet, dass der Schüler nicht vorbereitet ist und somit rät (Nullhypothese).
Ermitteln Sie den größtmöglichen Ablehnungsbereich, wenn die Wahrscheinlichkeit den Schüler zu Unrecht als
Lerner einzuschätzen kleiner als 1% sein soll.
Nullhypothese H0: Der Schüler rät die Antworten, er hat 50% richtige Antworten.
Testgröße: Anzahl der richtigen Antworten
Stichprobenlänge n = 25
Signifikanzniveau α ≤ 1%
Gesucht: Entscheidungsregel (rechtsseitiger Test)

Ablehungsbereich A = c + 1 .. 25
Annahmebereich A = 0 .. c
H0 p0 ≤ 0.5
Annahme von H0 , richtige Entscheidung
falsche Entscheidung, Fehler 1. Art, α
Tafelwerk, S. 27
T
SPBinTabelle ( 25 , 0.5)
=
0
0
2.98023·10 -8
1
7.7486·10 -7
2
9.71556·10 -6
3
7.82609·10 -5
4
0.00046
α = 1 − 0.97836 = 0.02164 > 1%
α = 1 − 0.99268 = 0.00732 < 1%
Der Ablehnungsbereich A = 0 .. 18 liefert einen Fehler 1. Art von 0,7%

Der Ablehnungsbereich A = 19 .. 25 liefert einen Fehler 1. Art von 0,7%
(9) Wahltag
Bei der letzten Wahl hat ein Kandidat 35% der Stimmen erhalten. Vor der kommenden Wahl wird eine Umfrage
durchgeführt, um zu ermitteln, ob dieser Kandidat dieses Mal mindestens genau so gut abschneidet
(Nullhypothese). Von 200 befragten Wählern seines Wahlkreises sagen 64, dass sie ihn wählen werden.
a) Bestimmen Sie den größtmöglichen Ablehnungsbereich der Nullhypothese für das Signifikanzniveau 5%.
Zu welcher Entscheidung kommt man durch das Testergebnis?
b) Beschreiben Sie, worin bei diesem Beispiel der Fehler 2. Art besteht.
Nullhypothese H0: Der Kandidat erhält mindestens 35%.
Testgröße: Anzahl der Wähler, die den Kandidaten wählen wollen.
Stichprobenlänge n = 200
Signifikanzniveau α = 5%
Gesucht: Entscheidungsregel (linksseitiger Test)

Ablehungsbereich A = 0 .. c
Annahmebereich A = c + 1 .. 200
H0 p0 ≥ 0.35
Annahme von H0 , richtige Entscheidung
falsche Entscheidung, Fehler 1. Art, α
Tafelwerk, S. 24
T
SPBinTabelle ( 200 , 0.35)
0
=
0
1
0
2
0
3
0
0
α = 0.05837 > 5%
α = 0.04262 < 5%

Der Ablehnungsbereich A = 0 .. 58 liefert einen Fehler 1. Art von 4,2%.
Somit folgert man, dass der Kandidat mindestens 35% aller abgegebenen Stimmen erhält.
(Man erwartet, dass H0 zutrifft.)
Der Fehler 2. Art besteht darin, den Kandidaten als ungeeignet zu erachten, obwohl er mindestens 35% aller
abgegebenen Stimmen erhalten wird.
(10) Call-Center
Ein Call-Center möchte seine Kundenfreundlichkeit verbessern. Nach Einbau einer neuen Telefonanlage und
Schulungen aller Mitarbeiter werden 200 zufällig ausgewählte Kunden nach Ihrer Zufriedenheit befragt. 130
Kunden waren mit dem Gebotenen zufrieden. Bisher waren 30% der Kunden unzufrieden mit dem Service.
Ein Mitarbeiter äußert die ketzerische Vermutung, dass sich nichts geändert hat.
Geben Sie die Testgröße T und die Nullhypothese H0 an. Bestimmen Sie den größtmöglichen
Ablehnungsbereich der Nullhypothese auf dem 5%-Niveau.
Stimmen Sie aufgrund dieses Tests unserem Ketzer zu?
Nullhypothese H0: Der Anteil der Unzufriedenen liegt (noch immer) bei 30%.
Testgröße T: Anzahl der Unzufriedenen.
Stichprobenlänge n = 200
Signifikanzniveau α = 5%
Gesucht: Entscheidungsregel (rechtsseitiger Test)

Ablehungsbereich A = c + 1 .. 200
Annahmebereich A = 0 .. c
H0 p0 = 0.3
Annahme von H0 , richtige Entscheidung
falsche Entscheidung, Fehler 1. Art, α
Tafelwerk, S. 19
T
SPBinTabelle ( 200 , 0.3)
0
=
0
1
0
2
0
3
0
4
0
0
α = 1 − 0.94579 = 0.05421 > 5%
α = 1 − 0.96037 = 0.03963 < 5%
Der Annahmebereich A = 0 .. 71 liefert einen Fehler 1. Art von 3,9%

Der Ablehnungsbereich A = 72 .. 200 liefert einen Fehler 1. Art von 3,9%
130 Kunden waren zufrieden, 70 unzufrieden. Also nehmen wir H0 an und überlegen uns weitere Verbesserungen.
Binomialkoeffizient:


bk ( n , k) := wenn  k < 1 , 1 ,
Wahrscheinlichkeit nach Bernoulli:
n
k


⋅ bk ( n − 1 , k − 1) 
k
PBinver ( n , p , k) := bk ( n , k) ⋅ p ⋅ ( 1 − p)
n− k
n: Anzahl der Versuche
p: Wahrscheinlichkeit für einen Treffer
k: Anzahl der Treffer
z
Summenwahrscheinlichkeit, höchstens z Treffer:
∑
SPBin_h ( n , p , z) :=
PBinver ( n , p , k)
k = 0
n
Summenwahrscheinlichkeit, mindestens z Treffer:
SPBin_m ( n , p , z) :=
∑
PBinver ( n , p , k)
k = z
F(n,p) in Tabellenform, für große n :
SPBinTabelle ( n , p) :=
k←0
b ← ( 1 − p)
n
m0 ← b
while k < n
k←k+1
b←
b ⋅ p ⋅ ( n − k + 1)
( 1 − p) ⋅ k
mk ← b
s←0
for k ∈ 0 .. n − 1
s ← s + mk
mk ← s
mn ← 1
m