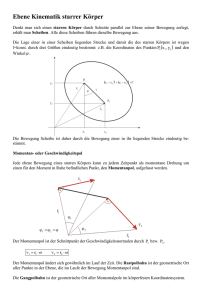
Starre Körper

K APITEL III
Lagrange-Formalismus: Anwendungen
In diesem Kapitel werden einige längeren Anwendungen des in Kap II vorgestellten LagrangeFormalismus diskutiert.
III.1 Starre Körper
Ein physikalischer Festkörper ist ein System aus vielen Atomen — für ein Stück auf menschlicher
Skala, etwa 1023 –1026 Atomen. Dementsprechend ist die Beschreibung als ein Mehrteilchensystem
wie in Abschn. I.6 unrealistisch. Stattdessen werden idealisierte Modelle des Festkörpers benutzt.
Eines davon ist das Modell eines starren Körpers. Dabei handelt es sich um ein System aus
(vielen) Massenpunkten ma mit konstanten Abständen zueinander. Diese Zwangsbedingungen über
die Abstände folgen aus inneren Kräften. Dank den letzteren bleibt die Anzahl der eigentlichen
Freiheitsgrade trotz der hohen Teilchenzahl immer klein im Modell (§ III.1.1). Für die Beschreibung
der globalen Bewegung des Körpers ist eine Kenntnis der inneren Zwangskräfte nicht nötig. Deshalb eignet sich die Lagrange’sche Vorgehensweise besser als der Newton’sche Formalismus, um die
Bewegungsgleichungen für den starren Körper herzuleiten (§ III.1.2).
In der Idealisierung eines starren Körpers ist das System definitionsgemäß nicht deformierbar.
Dementsprechend können im Rahmen des Modells Eigenschaften wie Elastizität, Plastizität. . . nicht
untersucht werden. Für solche Phänomene würde man den Körper eher als ein verformbares Kontinuum beschreiben. Dieser Kontinuum-Limes ist auch günstiger als die Beschreibung als eine Menge
von diskreten punktförmigen Teilchen, um einige Größen zu berechnen, die in der Bewegung von
Relevanz sind. Deshalb wird der Limes auch diskutiert.
III.1.1 Beschreibung des starren Körpers
III.1.1
a Anzahl der Freiheitsgrade
::::::::::::::::::::::::::::::::::
Das Modell des starren Körpers reduziert die a priori große (3N ) Anzahl der Freiheitsgrade
eines N -Teilchen-Systems zu einer kleinen Anzahl, und zwar meistens nur 6 für die Fälle, wo die
Vereinfachung von Nutze ist.
Im Fall von zwei Massenpunkten 1 und 2 mit der Zwangsbedingung eines zeitlich konstanten
Abstands |~x2 (t) − ~x1 (t)| besitzt das System insgesamt s = 3N − 1 = 5 Freiheitsgrade. Diese können
z.B. die drei Koordinaten des Schwerpunkts und zwei Winkel für die Orientierung des Verbindungsvektors zwischen 1 und 2 sein.
Falls es drei Massenpunkte 1, 2 und 3 mit drei entsprechenden Zwangsbedingungen über die
Abstände |~x2 (t) − ~x1 (t)|, |~x3 (t) − ~x1 (t)| und |~x3 (t) − ~x1 (t)| gibt, bleiben nach Berücksichtigung der
letzteren s = 3N − 3 = 6 Freiheitsgrade übrig. Beispielsweise kann man drei Schwerpunktskoordinaten betrachten, zusammen mit drei Winkeln für die Orientierung im Raum der Ebene, in welcher
die drei Massenpunkte liegen.(14)
Addiert man einen vierten Massenpunkt, so ist seine Position durch 3 Zwangsbedingungen
|~x4 (t)−~x1 (t)|, |~x4 (t)−~x2 (t)| und |~x4 (t)−~x3 (t)| völlig bestimmt — bis auf einer Spiegelung bezüglich
(14)
... im allgemeinen Fall, wo die drei Punkte nicht auf einer Gerade sitzen.
59
III.1 Starre Körper
der durch die drei ersten Punkte definierten Ebene. Somit gibt es immer noch 6 Freiheitsgrade.
Das gleiche gibt für eine beliebige Anzahl N ≥ 4. Wenn man einen N -ten Massenpunkt zu
N −1 schon anwesenden Punkten addiert, dann bestimmen drei Zwangsbedingungen |~xN (t)−~x1 (t)|,
|~xN (t) − ~x2 (t)| und |~xN (t) − ~x3 (t)| seine Position: die weiteren Abstände sind dadurch automatisch
festgelegt bzw. sind nicht unabhängig davon. Deshalb werden die drei möglichen Freiheitsgrade
dieses zusätzlichen Massenpunkts durch genau drei Bedingungen annulliert, d.h. die Anzahl der
Freiheitsgrade ändert sich nicht, und bleibt gleich 6.
Kontinuumlimes
Dank der Unabhängigkeit der Anzahl von Freiheitsgraden von der Anzahl N von Massenpunkten
für N ≥ 3 kann man problemlos den Limes N → ∞ betrachten, und danach zum Modell eines
Kontinuums übergehen. Im letzteren Fall entspricht der starre Körper einem endlichen kontinuierlichen Volumen, wie z.B. eine Vollkugel, das sich nicht verformen kann. Dementsprechend werden
einige Eigenschaften des Körpers durch (teilweise) stetige Funktionen vom Ort — insbesondere eine
Massendichte ρ(~r) —, die genau da ungleich Null sind, wo der Körper sich befindet.
Um den Grenzfall genauer zu definieren kann man zuerst das nicht-deformierbare kontinuierliche Medium als Zusammensetzung aus endlich vielen (N ) kleinen Massenstücken ma beschreiben,
die sich relativ zu einander nicht bewegen; seien ~xa ihre Ortsvektoren. Ersetzt man die
P Massenstückchen durch Massenpunkte, so hat man einen starren Vielteilchen-Körper. Sei M = a ma die
Gesamtmasse des Körpers.
Im Kontinuumlimes wird die Anzahl der Massenpunkte unendlich groß, N → ∞, und ihre
Massen werden unendlich klein , ma → 0, bei festgehaltener Gesamtmasse M . Im Grenzfall werden
Summen über a, d.h. über alle Massenpunkte, durch Integrale über das durch den Körper besetzte
Volumen V ersetzt. Genauer schreibt man für jede Funktion f der Position
Z
X
ma f ~xa → ρ(t,~r)f (~r) d3~r
(III.1)
V
a
mit ρ der Massendichte.
Bemerkung: Schreibt man
ρ(~r) =
X
ma δ (3) ~r − ~xa
a
mit δ (3)( ) der 3-dimensionalen Dirac-Distribution,(15) so kann man ein System aus diskreten Massenpunkten in der Sprache des Kontinuumlimes beschreiben.
III.1.1
b Kinematik des starren Körpers
:::::::::::::::::::::::::::::::::::::::
Zur Untersuchung der Bewegung eines starren Körpers ist es sinnvoll, zwei unterschiedliche
Bezugssysteme mit zugehörigen Koordinatensystemen einzuführen. Somit betrachtet man einerseits
ein raumfestes Inertialsystem BI , entsprechend z.B. einem inertialen Beobachter, der die Bewegung
des Körpers misst, ohne sich damit zu bewegen. Ortsvektoren relativ zu diesem System werden
~ a (t) für die Positionen der Massenpunkte des starren
hiernach mit Großbuchstaben bezeichnet, wie X
Körpers.
Andererseits wird auch ein körperfestes Bezugssystem B definiert, das sich zusammen mit dem
starren Körper bewegt. Insbesondere ist B nicht unbedingt Inertial, denn die Bewegung vom Körper
kann beschleunigt sein. In B wird dann ein Koordinatensystem gewählt, insbesondere ein Ursprungs~
punkt O, dessen Position bezüglich BI mit X(t)
bezeichnet wird. In der Praxis wird es günstig sein,
diesen Nullpunkt im Schwerpunkt des starren Körpers zu nehmen, obwohl dies nicht erforderlich
ist. Ortsvektoren relativ zu B werden mit Kleinbuchstaben denotiert, z.B. ~xa für die Positionen der
Massenpunkte des starren Körpers, die definitionsgemäß zeitunabhängig sind.
(15) (3)
δ
(~r) = δ(x)δ(y)δ(z) mit (x, y, z) den Koordinaten von ~r.
60
Lagrange-Formalismus: Anwendungen
Drei der für die Beschreibung des starren Körpers nötigen 6 Freiheitsgrade beschreiben die
Translationsbewegung des Ursprungspunkts O von B relativ zu BI , die drei anderen entsprechen
z.B. den Winkeln der Drehungen, die von den Achsen des Koordinatensystems in BI zu den Koordinatenachsen von B führen (vgl. § III.1.1 c).
Die Position eines Massenpunkts a des starren Körpers bezüglich des Inertialsystems kann jetzt
als
~ a (t) = X(t)
~
X
+ R(t)~xa
(III.2)
geschrieben werden, mit R der zeitabhängigen Drehmatrix, welche die Koordinatenachsen von B in
jene von BI transformiert. Eine Ableitung nach der Zeit gibt für die Geschwindigkeit relativ zu BI
[vgl. Gl. (I.34)]
~˙ a (t) = X(t)
~˙
X
+ R(t) ω
~ (t) × ~xa
(III.3)
mit ω
~ (t) der Winkelgeschwindigkeit der Rotationsbewegung des starren Körpers, wobei ~x˙ a = ~0
benutzt wurde.
III.1.1
c Euler-Winkel
:::::::::::::::::::::
der Vollständigkeit(?) halber....
weniger wichtig / dringend als andere Paragraphen!
III.1.2 Bewegungsgleichungen
III.1.2
a Kinetische Energie
:::::::::::::::::::::::::::
Die kinetische Energie des starren Körpers bezüglich des Inertialsystems BI ist die Summe aus
der kinetischen Energien der individuellen Massenpunkten, d.h.
X ma ˙
~ a (t)2 .
T =
X
2
a
~˙ a (t) substituiert werden
Dabei kann der Ausdruck (III.3) der Geschwindigkeit X
X ma ˙
2
~
T =
X(t)
+ R(t) ω
~ (t) × ~xa .
2
a
Die Berechnung des (Betrags)Quadrats liefert dann
X
X ma 2
1X
~˙
~˙ 2 + X(t)
T =
ma X(t)
· R(t) ω
~ (t) ×
ma ~xa +
R(t) ω
~ (t) × ~xa .
2 a
2
a
a
Fortsetzung folgt bald!
(III.4)