Komplexitätstheorie - Zentrum für Angewandte Informatik der

Informatik II
Komplexitätstheorie
Komplexitätstheorie
Rainer Schrader
Zentrum für Angewandte Informatik Köln
16. Februar 2009
1 / 58
2 / 58
Komplexitätstheorie
Komplexitätstheorie
• im verbleibenden Teil der Vorlesung wollen wir uns mit einer groben
Einteilung beschäftigen, die Fragestellungen als „leicht” und „schwer”
klassifiziert
Gliederung
• das Kriterium dazu ist die Laufzeit, die benötigt wird, um die
• Einführung
• polynomielle Reduktionen
Fragestellung zu beantworten (bzw. zu entscheiden, ob ein gegebenes
x in einer Sprache L liegt)
• NP-Vollständigkeit von SAT
• weitere NP-vollständige Probleme
• wir werden dabei akzeptieren, dass die Antwort länger dauern darf,
wenn x lang ist
• wir fordern jedoch, dass die Laufzeit nicht mit der Inputlänge explodiert,
sondern moderat ansteigt
3 / 58
4 / 58
Komplexitätstheorie
Komplexitätstheorie
• die Komplexitätstheorie
• beruht weiterhin auf der Turingmaschine als Rechnermodell
• beschäftigt sich ausschließlich mit berechenbaren Problemen
• hier ist ein Beispiel für ein Entscheidungsproblem:
• klassifiziert diese nach ihren Schwierigkeitsgraden
• eine Clique der Größe k ist eine Teilmenge V 0 ⊆ V mit
• |V 0 | = k und
• (d.h. nach dem Zeit- und Speicherplatzbedarf zu ihrer Lösung)
• {u, v } ∈ E für alle u, v ∈ V 0 , u 6= v
• und benutzen wir die Begriffe „Turingmaschine” und „Algorithmus”
synonym
CLIQUE
• wir beschränken uns zunächst
Instanz: ungerichteter Graph G = (V , E ) und k ∈ N
• auf Entscheidungsprobleme (formalisiert als Sprachen wie im
letzten Kapitel)
Frage: besitzt G eine Clique der Größe mindestens k ?
• auf den Zeitbedarf
6 / 58
5 / 58
Komplexitätstheorie
Komplexitätstheorie
Beispiel: Der folgende Graph
2
1
• sei G = (V , E ), k eine Instanz des Cliquenproblems
• wir können diese Instanz wie gezeigt binär kodieren als
3
code(G = (V , E ), k )
6
5
• und dem Cliquenproblem eine Sprache zuordnen:
4
L = {code(G = (V , E ), k ) : G hat eine Clique der Größe mindestens k }
enthält eine eine Clique der Größe 3, aber keine Clique der Größe 4.
• jede Instanz des Cliquenproblems kann bei kanonischer
• damit haben wir das Cliquenpoblem auf ein Spracherkennungsproblem
Knotennumerierung 1, 2, . . . , |V | durch die Liste der Endknoten der
Kanten {i , j }, hier:
zurückgeführt
• in weiteren werden wir uns auf Entscheidungsprobleme konzentrieren
• und ignorieren die Kodierung und das zugrundeliegende
12 13 14 15 16 23 24 26 35 45 56
sowie Angabe von k kodiert werden
Spracherkennungsproblem
• d.h. es reichen (im Wesentlichen) n = 2|E | log |V | + log k Bits zur
Spezifikation einer Instanz
7 / 58
8 / 58
Komplexitätstheorie
Komplexitätstheorie
Zeitbedarf
Laufzeit einer DTM:
• sei L eine Sprache
• sei M eine DTM, die L entscheidet
• für x ∈ Σ∗ sei T M (x ) die Anzahl der Rechenschritte, die M bis zum
• als Zeitbedarf fassen wir die Anzahl der Schritte auf, die eine
Turingmaschine benötigt, um ein Problem zu lösen
• der Zeitbedarf wird eine Funktion vom Input x sein
• wie in „Informatik I” sind wir weniger an konkreten Aussagen für jedes
Entscheiden von x ausführt
x interessiert
• sondern am Verhalten für alle Inputs gleicher Länge
• wir werden daher Schranken in Abhängigkeit von der Anzahl der Bits
• sei t : N → N
• M heißt t (n)-zeitbeschränkt, falls T M (x ) ≤ t (|x |)
• d.h. in Abhängigkeit von der Länge |x |
• wir messen somit den maximal benötigten Zeitbedarf bei einem Input
• für alle Inputs x der Länge |x | = n gilt:
• anschaulich:
des Inputs herleiten
• M hält nach höchstens t (n) Schritten
mit n bits
9 / 58
10 / 58
Komplexitätstheorie
Komplexitätstheorie
Laufzeit einer NDTM:
• wir lassen also zu, dass der Zeitbedarf eine Funktion der Größe n der Instanz ist
• die folgende Tabelle gibt einen Eindruck der Wachstumsraten für verschiedene
• sei L eine Sprache
• sei M eine NDTM, die L akzeptiert
• sei
T M (x ) =

min{Länge einer akzeptierenden Berechnung},
0,
solche Funktionen („Laufzeitfunktionen“):
falls x ∈ L
sonst
n
• anschaulich: für x ∈ L ist die Laufzeit die Anzahl der Rechenschritte,
n2
die M auf einem kürzesten Weg bis zum Akzeptieren von x ausführt
n3
• für t : N → N heißt M t (n)-zeitbeschränkt, falls T M (x ) ≤ t (|x |)
n5
• anschaulich:
2n
3n
• für alle Inputs x der Länge |x | = n gilt:
• für x ∈ L existiert eine akzeptierende Berechnung, die höchstens
t (n) Schritten ausführt
11 / 58
10
0,00001
sek
0,0001
sek
0,001
sek
0,1
sek
0,001
sek
0,059
sek
20
0,00002
sek
0,0004
sek
0,008
sek
3,2
sek
1
sek
58
min
30
0,00003
sek
0,0009
sek
0,027
sek
24,3
sek
17,9
min
6,5
Jahre
40
0,00004
sek
0,0016
sek
0,064
sek
1,7
min
12,7
Tage
3855
Jahrhund.
50
0,00005
sek
0,0025
sek
0,125
sek
5,2
min
35,7
Jahre
2 × 108
Jahrhund.
60
0,00006
sek
0,0036
sek
0,216
sek
13,0
min
366
Jahrhund.
1, 3 × 1013
Jahrhund.
12 / 58
Komplexitätstheorie
Komplexitätstheorie
• nun betrachten wir den Effekt von verbesserter Computertechnologie im gleichen
Szenario
• wir zeigen jeweils die größte Probleminstanz, die in einer Stunde gelöst werden
• für das Cliquenproblem sind nur Algorithmen mit exponentieller Laufzeit
kann, wenn Computer 100 bzw. 1000 mal schneller sind als unsere derzeitigen
Laufzeitfunktion
n
n2
n3
n5
2n
3n
derzeitiger
Computer
N1
N2
N3
N4
N5
N6
100 mal schneller
Computer
100N1
10N2
4,64N3
2,5N4
N5 + 6,64
N6 + 4,19
bekannt, d.h. es ist hoffungslos, sehr große Instanzen praktisch zu lösen
• die Komplexitätstheorie hilft uns, zu verstehen, warum wir uns so
1000 mal schneller
Computer
1000N1
31,6N2
10N3
3,98N4
N5 + 9,97
N6 + 6,29
schwer damit tun, gute Algorithmen für viele Probleme zu finden
• als „gut” bezeichnen wir Algorithmen mit polynomieller Laufzeit
• sie gibt uns Techniken, für neue Probleme festzustellen, ob sie im
Wesentlichen genauso schwierig wie das Cliquenproblem sind
Wir sehen den gewaltigen Unterschied zwischen polynomiellen und exponentiellen
Laufzeitfunktionen.
13 / 58
14 / 58
Komplexitätstheorie
Komplexitätstheorie
P und NP
• P ist die Menge aller Sprachen, die
• von einer deterministischen Turingmaschine
entschieden werden,
Gliederung
• Einführung
• polynomielle Reduktionen
• deren Laufzeit durch ein Polynom in der Länge des Inputs
beschränkt ist
• NP-Vollständigkeit von SAT
• weitere NP-vollständige Probleme
• NP ist die Menge aller Sprachen, die
• von einer nichtdeterministischen Turingmaschine
akzeptiert werden,
• deren Laufzeit durch ein Polynom in der Länge des Inputs
beschränkt ist
15 / 58
16 / 58
Komplexitätstheorie
Komplexitätstheorie
• wir wollen Entscheidungsprobleme betrachten
Beispiele für Sprachen in P:
• {(x1 , . . . , xn , π) | π ist Permutation, die die xi monoton steigend anordnet}
• {(G(V , E ), c, T ) : T ist ein minimal aufspannender Baum im Graphen G}
• {(G(V , E ), c, P ) : P ist ein kürzester Weg im Graphen G}
• d.h. wir suchen:
• bestimmte Objekte aus einer Menge,
• die eine bestimmte Eigenschaft erfüllen
• (z.B. Cliquen der Größe mindestens k )
Erläuterung zum Sortieren:
• das Entscheidungproblem ist in NP, wenn gilt:
• Kodierung des Inputs: x1 , . . . , xn , π
P
P
• Länge der Kodierung: ni=1 log(xi ) + n + ni=1 log(i ) + n Bits
• Lufzeit zum Sortieren, z.B.: O(n log n) = Polynom(Inputlänge)
• rate eine Objekt
• teste in polynomieller Zeit, ob es in der Menge liegt
• teste in polynomieller Zeit, ob es in die Eigenschaft hat
Beispiele für Sprachen, die nicht offensichtlich in P liegen, folgen später.
17 / 58
18 / 58
Komplexitätstheorie
Komplexitätstheorie
Bemerkungen
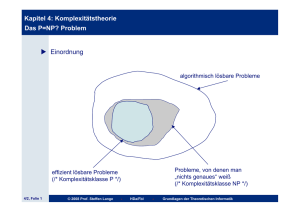
• offensichtlich gilt P ⊆ NP
• es ist unbekannt, ob P = NP oder P 6= NP gilt
• wie bei den berechenbaren Funktionen wollen wir dazu die Struktur von
NP näher zu untersuchen
• diese Frage gilt als das wichtigste offene Problem der Theoretischen
• bisher wissen wir lediglich, dass P ⊆ NP
Informatik
• das Clay Mathematics Institute (CMI) in Cambridge, MA, hat für seine
• wir versuchen den Reduzierbarkeitsbegriff sinnvoll zu übertragen
Lösung einen Preis von 1 Mio $ ausgesetzt
• die von einer großen Mehrheit akzeptierte Arbeitshypothese ist P 6= NP
• wir werden im Folgenden einen Einblick gewinnen, warum das so ist
19 / 58
20 / 58
Komplexitätstheorie
Komplexitätstheorie
• wie „” ist auch „p ” transitiv, denn:
• seien L und L0 zwei Sprachen
• „” ist transitiv
• L heißt polynomiell reduzierbar auf L0 , falls gilt:
• das Produkt von zwei Polynomen ist ein Polynom
• L ist reduzierbar auf L0 mittels einer Funktion f
• d.h. x ∈ L ⇐⇒ f (x ) ∈ L0
• L und L0 heißen polynomiell äquivalent, falls L p L0 und L0 p L
• Notation: L ≡p L0
• f ist in polynomieller Zeit berechenbar
• L heißt NP-schwer, falls für alle L0 ∈ NP gilt: L0 p L
• Notation: L p L0
• L heißt NP-vollständig, falls L NP-schwer ist und L ∈ NP
22 / 58
21 / 58
Komplexitätstheorie
Komplexitätstheorie
Lemma
Sei
Lemma
L NP-vollständig.
Sei L NP-vollständig.
(i) L ∈ P ⇐⇒ P = NP
(i) L ∈ P ⇐⇒ P = NP
(ii) L0 ∈ NP und L p L0 =⇒ L0 ist NP-vollständig
(ii) L0 ∈ NP und L p L0 =⇒ L0 ist NP-vollständig
(iii) L und L0 NP-vollständig =⇒ L ≡p L0 .
(iii) L und L0 NP-vollständig =⇒ L ≡p L0 .
Beweis von (i):
Beweis von (ii) und (iii):
• sei L ∈ P und L0 ∈ NP
• dann ist L0 polynomiell reduzierbar auf L vermittels einer Funktion f
• insbesondere ist f polynomiell deterministisch berechenbar
• (ii) sei L00 ∈ NP
• es ist L00 p L p L0
• somit ist auch L0 NP-vollständig.
• zu gegebenem x berechne f (x ) und teste in polynomieller Zeit, ob
f (x ) ∈ L.
• (iii) folgt aus der Definition
• damit ergibt sich ein polynomieller Test, ob x ∈ L0
• die Umkehrung gilt offensichtlich
23 / 58
24 / 58
Komplexitätstheorie
Komplexitätstheorie
• mit den NP-vollständigen Problemen haben wir den harten Kern der
Gliederung
Probleme in NP ausgezeichnet, denn
• sie sind alle „gleich schwierig”
• Einführung
• polynomielle Reduktionen
• und ist eines „einfach”, so sind alle Problem in NP „einfach”
• NP-Vollständigkeit von SAT
• weitere NP-vollständige Probleme
• wir wissen aber noch nicht, ob diese Teilmenge nichtleer ist
25 / 58
26 / 58
Komplexitätstheorie
Komplexitätstheorie
• sei X = {x1 , x2 , . . . , xn } eine Menge Boolescher Variablen
• wollen wir also 1 Mio $ verdienen, so reicht es, für ein beliebiges
• eine Klausel ist eine Disjunktion von Literalen der Form xi oder
NP-vollständiges Problem A eine der beiden Alternativen zu zeigen:
(1) A ∈ P
oder
x i über X
(2) A ∈
/P
• z.B. sind folgende Ausdrücke Klauseln über X = {x1 , x2 }:
• im Fall (1) folgt P = NP, im Fall (2) folgt P 6= NP
• jetzt fehlt nur noch ein erstes NP-vollständiges Problem
K1 = x1 ∨ x 2
K2 = x 1 ∨ x2
K3 = x1 ∨ x2
K4 = x 1
• eine Boolesche Funktion ist in konjunktiver Normalform (KNF), wenn
sie als Konjunktion von Klauseln ausgedrückt ist
• als Vorbereitung erinnern wir uns an die im Kapitel Rechnerarchitektur
• die neue Definition unterscheidet sich von der früheren nur dadurch,
eingeführten Booleschen Funktionen
dass Klauseln nun auch weniger als n Literale haben dürfen
• ein wenig anders als dort definieren wir die konjunktive Normalform
(KNF) wie folgt:
• z.B. entspricht die KNF gegeben durch X = {x1 , x2 } und
C = {c1 , c2 } der Funktion f = (x1 ∨ x 2 ) ∧ (x 1 ∨ x2 )
27 / 58
28 / 58
Komplexitätstheorie
Komplexitätstheorie
Erfüllbarkeitsproblem SAT (satisfiability)
• eine KNF f ist erfüllbar, wenn es eine Belegung der Variablen
(x1 , x2 , . . . , xn ) gibt, so dass f den Wert 1 hat
Instanz:
• für eine KNF f bedeutet das offensichtlich:
Frage:
f erfüllbar ⇐⇒ alle Klauseln der KNF erfüllbar
eine Menge X = {x1 , x2 , . . . , xn } von Booleschen Variablen und
eine Menge C = {K1 , K2 , . . . , Km } von Klauseln über X
V
ist F = m
i =1 Ki erfüllbar?
Satz (Cook)
SAT ist NP-vollständig.
Beispiele:
• die KNF f = (x1 ∨ x 2 ) ∧ (x 1 ∨ x2 ) ist erfüllbar, denn es gilt f = 1 für
Beweisidee:
x1 = x2 = 1 (oder x1 = x2 = 0)
• (i) SAT ist in NP:
• die KNF f = (x1 ∨ x 2 ) ∧ (x1 ∨ x2 ) ∧ x 1 ist dagegen nicht erfüllbar
• rate eine Belegung der Variablen
• prüfe nach, ob B mit dieser Belegung den Wert 1 hat
• (um die letzte Klausel zu erfüllen, muss x1 = 0 sein, für x2 = 0 ist die
zweite Klausel nicht erfüllt, für x2 = 1 ist die erste Klausel nicht erfüllt)
• damit ist SAT ∈ NP
29 / 58
30 / 58
Komplexitätstheorie
Komplexitätstheorie
(ii) SAT ist NP-schwer, d.h. für jedes L ∈ NP gilt: L p SAT :
• der Beweis ist etwas technisch, aber die Idee ist recht einfach
Gliederung
• von einem L ∈ NP wissen wir nur, dass eine NDTM M existiert, die
L in polynomieller Zeit akzeptiert
• wir definieren zu einem Input x eine KNF f , die die Arbeitsweise von
• Einführung
• polynomielle Reduktionen
• die KNF hat eine Länge, die durch ein Polynom in |x | beschränkt ist
• NP-Vollständigkeit von SAT
• weitere NP-vollständige Probleme
M auf x simuliert
• die KNF ist erfüllbar, genau dann wenn M mit Input x akzeptiert
• damit ist x ∈ L ⇐⇒ f (x ) = 1
• d.h. SAT ist NP-schwer.
31 / 58
32 / 58
Komplexitätstheorie
Komplexitätstheorie
Satz
3-SAT ist NP-vollständig.
• die Aussage des Satzes von Cook lässt sich noch etwas verschärfen
• sei f eine Boolesche Formel in konjunktiver Normalform
Beweis:
• f heißt 3-KNF , falls in jeder Klausel höchstens drei Literale
• sei K = y1 ∨ · · · ∨ ys eine Klausel mit yi ∈ {x1 . . . xn , x 1 , . . . , x n } und
vorkommen.
• Beispiel:
• sei
s≥4
• sei z eine neue Variable
• betrachte die Boolesche Funktion
f = (x1 ∨ x2 ∨ x3 ) ∧ (x2 ∨ x3 ) ∧ (x1 ∨ x2 ∨ x3 )
K1 = (y1 ∨ · · · ∨ ys−2 ∨ z ) ∧ (ys−1 ∨ ys ∨ z )
3-SAT = {f : f ist eine erfüllbare 3-KNF}.
• offensichtlich gilt:
Satz
• K1 ist in konjunktiver Normalform
• K hat eine erfüllende Belegung ⇐⇒ K1 hat eine erfüllende
Belegung
3-SAT ist NP-vollständig.
• K1 enthält nur Klauseln der Länge s − 1
33 / 58
34 / 58
Komplexitätstheorie
Komplexitätstheorie
• per Induktion folgt:
• sei K eine Klausel der Länge s ≥ 4
• K kann durch eine Boolesche Formel K 0 ersetzt werden, so dass
• mit Hilfe von 3-SAT wollen wir eine graphentheoretische Fragestellung als
NP-vollständig nachweisen
• sei G = (V , E ) ein Graph
• eine Teilmenge U ⊆ V von Knoten heißt unabhängig oder stabil , falls keine
• K 0 ist eine 3-KNF
• K 0 hat s − 3 neue Variablen
• K 0 besteht aus s − 2 Klauseln
zwei Knoten aus U durch eine Kante in E verbunden sind
• K hat eine erfüllende Belegung ⇐⇒ K 0 hat eine erfüllende
Belegung
• wir führen diese Reduktion für jede Klausel mit mehr als drei Variablen
durch
• dadurch entsteht eine polynomiell beschränkte Menge von Klauseln
und polynomiell viele neue Variablen
• dies liefert eine polynomiell berechenbare Abbildung g mit
• sei UM = {(G, k ) : G enthält eine stabile Menge der Größe mindestens k }
f ∈ SAT ⇐⇒ g(f ) ∈ 3-SAT
35 / 58
36 / 58
Komplexitätstheorie
Komplexitätstheorie
Beispiel:
• Sei
f = (x1 ∨ x2 ∨ x3 ) ∧ (x1 ∨ x2 ∨ x3 ) ∧ (x1 ∨ x2 ∨ x3 )
Satz
• der zu f gehörige Graph G ist:
UM ist NP-vollständig.
x3
Beweis:
• wir reduzieren 3-SAT auf UM
• sei B eine Boolesche Formel in 3-KNF mit Klauseln C1 , C2 , . . . , Cm .
• zu B konstruieren wir einen Graphen G = (V , E ) wie folgt:
x1
x2
x3
x1
x2
x1
x2
• für jede Klausel Ci enthält G ein Dreieck, wobei die Knoten dieses
Dreiecks mit den Literalen in Ci bezeichnet werden
x3
• zwei Knoten werden durch eine Kante verbunden, wenn sie
• sei k = m (Anzahl der Klauseln)
• höchstens ein Knoten eines Dreiecks liegt in einer unabhängigen Menge
komplementären Literale entsprechen
• daher ist die Kardinalität einer unabhängigen Menge in G höchstens
m.
38 / 58
37 / 58
Komplexitätstheorie
Komplexitätstheorie
• sei G = (V , E ) ein Graph
• eine Teilmenge C ⊆ V von Knoten heißt Clique , falls je zwei Knoten
• wir behaupten: G enthält eine unabhängige Menge der Größe
m genau dann, wenn B erfüllbar ist
aus C durch eine Kante in E verbunden sind.
• sei CLIQUE
• sei dazu U eine unabhängige Menge der Größe m
• U enthält genau einen Knoten von jedem Dreieck und keine zwei
= {(G, k ) : G enthält eine Clique der Größe mindestens k }
• offensichtlich gilt:
Knoten, die komplementären Literalen entsprechen
• setzen wir die Literale, die den Knoten in U entsprechen, auf „wahr”,
Clique in G = (V , E ) ↔ unabhängige Menge in G 0 = (V , E 0 )
so erhalten wir eine Belegung, die B erfüllt
• wobei G 0 = (V , E 0 ) mit e ∈ E 0 ⇐⇒ e ∈
/ E der komplementäre
Graph ist
• ist umgekehrt x eine Wahrheitsbelegung, die B erfüllt
• dann hat mindestens eine Variable in jedem Dreieck den Wert „wahr”
• und keine zwei komplementären Literale sind „wahr”
• ist U eine Teilmenge von Knoten, die in jedem Dreieck genau eine
wahre Variable hat, so ist U unabhängig.
39 / 58
40 / 58
Komplexitätstheorie
Komplexitätstheorie
• das Mengenüberdeckungsproblem „MÜP” spielt eine wichtige Rolle bei
der Optimierung von Schaltkreisen
• wir haben MÜP damals als Optimierungsproblem definiert
• bereits eine einfache „Entscheidungsvariante“ von MÜP ist
• Damit folgt:
NP-vollständig:
MÜP
Korollar
CLIQUE ist NP-vollständig.
2
Instanz:
endliche Menge U = {u1 , u2 , . . . , us }, eine Teilmengenfamilie
M = {M1 , M2 , . . . , Mk } ⊆ 2U , Zahl t ≤ k
Frage:
∗
∗
gibt
S es eine Teilfamilie M ⊆ M mit |M | = t , so dass
M ∈M∗ M = U ?
41 / 58
42 / 58
Komplexitätstheorie
Komplexitätstheorie
• sei (X , C) eine 3-SAT-Instanz mit Variablenmenge
Satz
X = {x1 , x2 , . . . , xn } und Klauselmenge C = {K1 , K2 , . . . , Km }
MÜP ist NP-vollständig.
• wir konstruieren (in polynomieller Zeit) dazu eine MÜP-Instanz
(U, M, t ) wie folgt:
Beweis:
U = {1, 2, . . . , m, m + 1, m + 2, . . . , m + n}
(i) MÜP ist in NP:
• rate eine Teilfamilie M∗
• prüfe, ob M∗ eine Überdeckung liefert
(d.h. s = m + n)
• für jedes i ∈ {1, 2, . . . , n} seien
• prüfe, ob |M | = t
• die Überprüfungen können in polynomieller Zeit durchgeführt werden
∗
Ti
Ti 0
• also gilt MÜP ∈ NP
=
=
{j | xi kommt in Klausel Kj vor} ∪ {m + i },
{j | x i kommt in Klausel Kj vor} ∪ {m + i }.
• dann sei
(ii) MÜP ist in NP-schwierig:
M = {T1 , T10 , T2 , T20 , . . . , Tn , Tn0 }
• wir zeigen 3-SAT ≤p MÜP
(d.h. k = 2n)
• und sei t = n.
43 / 58
44 / 58
Komplexitätstheorie
U
Ti
Ti 0
M
t
=
=
=
=
=
Komplexitätstheorie
{1, 2, . . . , m, m + 1, m + 2, . . . , m + n}
{j | xi kommt in Klausel Kj vor} ∪ {m + i },
{j | x i kommt in Klausel Kj vor} ∪ {m + i }
{T1 , T10 , T2 , T20 , . . . , Tn , Tn0 }
n
• sei M∗ = {M1 , M2 , . . . , Mn } eine Lösung von MÜP
• dann wird für jedes 1 ≤ i ≤ n das Element m + i genau einmal
• sei (a1 , a2 , . . . , an ) ∈ {0, 1}n eine erfüllende Belegung der Variablen
(x1 , x2 , . . . , xn )
Mi =
=
=
=
=
=
(U, M, t ) hat eine Lösung =⇒ (X , C) erfüllbar:
(X , C) erfüllbar =⇒ (U, M, t ) hat eine Lösung:
• für i = 1, . . . , n wähle
U
Ti
Ti 0
M
t
{1, 2, . . . , m, m + 1, m + 2, . . . , m + n}
{j | xi kommt in Klausel Kj vor} ∪ {m + i },
{j | x i kommt in Klausel Kj vor} ∪ {m + i }
{T1 , T10 , T2 , T20 , . . . , Tn , Tn0 }
n
überdeckt

Ti ,
Ti 0 ,
• d.h. M∗ enthält genau eine der Mengen Ti , Ti0
• nach Umnumerieren gilt Mi ∈ {Ti , Ti0 } für i = 1, . . . , n
• für i ∈ {1, 2, . . . , n} setze
falls xi = 1
falls xi = 0
• nach Konstruktion gilt |M∗ | = n = t und
S

M ∈M∗ M = U
xi =
1
0
falls Mi = Ti
falls Mi = Ti0
• dann enthält jede Klausel ein Literal mit Wert 1 und (X , C) hat eine
erfüllende Belegung.
46 / 58
45 / 58
Komplexitätstheorie
Komplexitätstheorie
Wir erklären nun informell, wie man den Begriff der NP-Schwierigkeit auf
Optimierungsprobleme ausdehnen kann:
• wir nehmen an, dass zur Lösung des Optimieringsproblems ein „Orakel”
Beispiel
existiert
Das Problem MENGENÜBERDECKUNG ist NP-schwierig:
• diese Orakel liefert optimale Lösungen in konstanter Zeit
• mit Hilfe dieses Orakles entwirft man einen deterministischen
• zur Lösung von MÜP verwende MENGENÜBERDECKUNG mit
Einheitskosten c(Mi ) = 1 für 1 ≤ i ≤ n
polynomiellen Algorithmus für ein NP-vollständiges Problem,
• dieser Algorithmus verwendet das Orakel als ein Unterprogramm
• wenn man das Orakel durch einen polynomiellen Algorithmus realisiert
• damit könnte MÜP mit einem Aufruf von MENGENÜBERDECKUNG
gelöst werden
könnte,
• dann würde dies die polynomielle Lösbarkeit des NP-vollständigen
Problems implizieren
• und somit P = NP.
47 / 58
48 / 58
Komplexitätstheorie
Komplexitätstheorie
• die nächste Aussage gibt eine interessante Zusatzinformation über die
Komplexität des Wortproblems für formale Sprachen
• wir haben im letzten Kapitel gesehen, dass das Wortproblem
Wir erwähnen an dieser Stelle noch zwei weitere Entscheidungsprobleme,
die wir im Kapitel Rechnerarchitektur besprochen haben:
• für Typ-0-Sprachen nicht entscheidbar ist
• für Typ-1-Sprachen entscheidbar ist und
• EULER-KREIS liegt in P
• HAMILTON-KREIS ist NP-vollständig
• für Typ-2- und Typ-3-Sprachen in polynomieller Zeit entscheidbar
ist
• Details in der Spezialvorlesung über Theoretische Informatik
• der im Beweis für Typ-1-Sprachen angegebene Algorithmus hat eine
exponentielle Laufzeit
• wir zeigen jetzt, dass diese Laufzeit wohl auch nicht zu verbessern ist
(es sei denn, P = NP)
50 / 58
49 / 58
Komplexitätstheorie
Komplexitätstheorie
• wir ordnen M einen LBA M 0 zu
• dazu erweitern wir einen Input x um weitere Blanks
• d.h. wir identifizieren x1 , . . . , xn mit 2p(n) x1 x2 . . . xn 2p(n)−n
Satz
Das Wortproblem für Typ-1-Sprachen ist NP-schwierig.
• M 0 gestartet mit 2p(n) x1 x2 . . . xn 2p(n)−n verhält sich wie M gestartet
Beweisskizze:
mit x1 , . . . , xn
• wir haben bereits gezeigt: „LBA-akzeptiert ⇐⇒ Typ-1”
• sei L ∈ NP beliebig
• zu M 0 gibt es eine äquivalente Typ-1-Grammatik GM 0
• damit gilt:
• dann gibt es zu ist L eine NDTM M , die L in polynomieller Zeit
akzeptiert
x ∈ L(M ) ⇐⇒
• sei p das zugehörige Polynom
51 / 58
2p(n) x1 . . . xn 2p(n)−n ∈ L(M 0 )
⇐⇒
S ⇒∗ x, . . . , xn
⇐⇒
x ∈ L(GM 0 )
52 / 58
Komplexitätstheorie
x ∈ L(M ) ⇐⇒
Komplexitätstheorie
2p(n) x1 . . . xn 2p(n)−n ∈ L(M 0 )
⇐⇒
S ⇒∗ x, . . . , xn
⇐⇒
x ∈ L(GM 0 )
• es gibt derzeit über 3000 Probleme, deren NP-Vollständigkeit bzw.
NP-Schwierigkeit bewiesen wurde
• die Funktion, die x die Grammatik GM 0 sowie das Wort
• für keines konnte die Mitgliedschaft in P nachgewiesen werden
2p(n) x 2p(n)−1 zuordnet, ist in polynomieller Zeit berechenbar
• damit festigt sich die Überzeugung, dass P 6= NP gilt
• sie liefert eine polynomielle Reduktion von L auf das Wortproblem für
• und die Suche nach einem (deterministischen) polynomiellen
Typ-1-Sprachen
Algorithmus für ein NP-schwieriges Problem nicht sehr erfolgreich sein
wird
• es ist unbekannt, ob das Wortproblem für Typ-1-Sprachen in NP liegt
• eventuell ist es noch schwieriger als die NP-vollständigen Probleme
53 / 58
Komplexitätstheorie
54 / 58
Komplexitätstheorie
1. Szenario Der Algorithmenspezialist hat keine Ahnung von Komplexitätstheorie. Er strampelt sich wochenlang ab und muss dann so vor seinen Chef
treten:
• die erste „Bibel“ für die Theorie der NP-Vollständigkeit ist das Buch
Michael R. Garey and David S. Johnson,
Computers and Intractability – A Guide to the Theory of NP-Completeness,
W. H. Freeman, 1979.
• aus diesem Buch stammen Teile dieser Kurzdarstellung
• die Autoren beschreiben den praktischen Nutzen in einem Cartoon:
• ein Algorithmenspezialist in einer Firma erhält die Aufgabe, einen
„Ich kann keinen effizienten Algorithmus finden. Ich fürchte, ich bin einfach zu dumm.”
effizienten Algorithmus für ein NP-schwieriges Problem aus der Praxis
zu finden. (Die meisten Praxisprobleme sind NP-schwierig!)
Hier muss man wohl um seine Karriere fürchten.
55 / 58
56 / 58
Komplexitätstheorie
Komplexitätstheorie
3. Szenario
• er kennt die Komplexitätstheorie und hat während seines Studiums
2. Szenario Mit einer geringen Wahrscheinlichkeit (das gelingt fast nie) kann
er beweisen, dass das Problem nicht in sub-exponentieller Zeit lösbar ist, dann
hat er natürlich bessere Karten:
fleißig NP-Schwierigkeitsbeweise geübt
• es fällt ihm daher nicht schwer, die NP-Schwierigkeit des vorliegenden
Problems zu beweisen
• dann hat er einen fast so guten Auftritt wie im zweiten Szenario:
„Ich kann keinen effizienten Algorithmus finden, weil das unmöglich ist.”
„Ich kann keinen effizienten Algorithmus finden, aber diese berühmten Leute können
das auch nicht.”
Aber, wie gesagt, ein solcher Erfolg wäre schon sehr ungewöhnlich.
Zumindest wäre dem Chef dann klar, dass es nichts nützt, ihn zu feuern und
einen anderen Algorithmenspezialisten einzustellen.
57 / 58
58 / 58