Kapitel 4: Komplexitätstheorie Das P=NP? Problem Einordnung

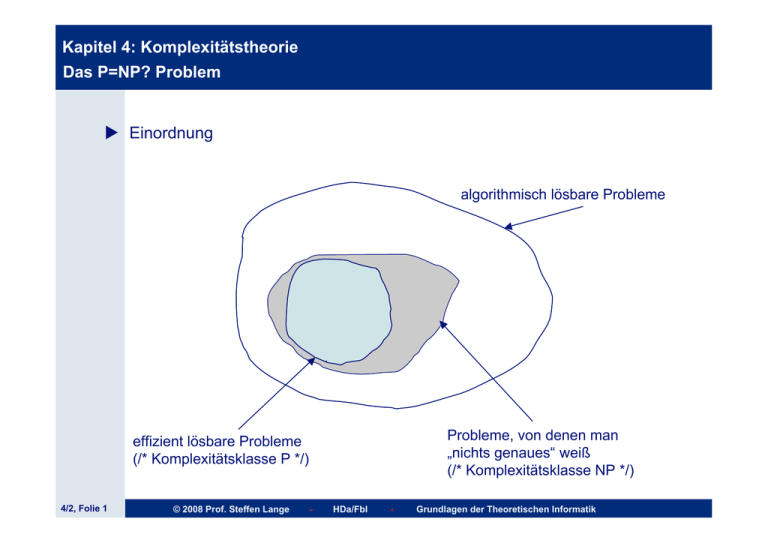
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Einordnung
algorithmisch lösbare Probleme
Probleme, von denen man
„nichts genaues“ weiß
(/* Komplexitätsklasse NP */)
effizient lösbare Probleme
(/* Komplexitätsklasse P */)
4/2, Folie 1
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem (mit Blick auf Suchprobleme)
... es sei R ⊆ { 0,1 }* × { 0,1 }* eine polynomiell beschränkte Relation
... beim zu R gehörenden Suchproblem geht es darum, zu jedem x ∈ X
eine Lösung y ∈ R(x) zu finden (/* falls es eine solche gibt */)
 Suchprobleme mit effizient verifizierbaren Lösungskandidaten
Das zu R gehörende Suchproblem hat effizient verifizierbare Lösungskandidaten, wenn es einen Algorithmus V und ein Polynom p(.,.) gibt, so daß
für alle x, y ∈ { 0,1 }* gilt:
•
•
•
4/2, Folie 2
wenn y ∈ R(x) gilt, so gibt V die Zahl 1 aus und stoppt
wenn y ∉ R(x) gilt, so gibt V die Zahl 0 aus und stoppt
die Rechenzeit von V bei Eingabe x, y ist kleiner gleich p(|x|)
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem (mit Blick auf Suchprobleme)
Suchprobleme mit effizient
verifizierbaren Lösungskandidaten
effizient lösbare Suchprobleme
... die Frage, ob P = NP gilt, ist – mit Blick auf Suchprobleme – äquivalent zur
Frage, ob es schwieriger ist eine Lösung zu finden oder zu überprüfen, ob ein
Lösungskandidat eine Lösung ist
4/2, Folie 3
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
... die Komplexitätsklassen P und NP umfassen traditionell alle algorithmisch
lösbaren Entscheidungsprobleme, für die es Lösungsalgorithmen gibt, die
bestimmten Anforderungen an die von ihnen benötigte Rechenzeit genügen
... dabei steht P für polynomielle Rechenzeit mit Blick auf deterministische
Turing-Maschinen und NP für polynomielle Rechenzeit mit Blick auf nichtdeteministische Turing-Maschinen
 Entscheidungsprobleme (allgemein)
Ein Paar (S+,S-) mit S+,S- ⊆ { 0,1 }* und S+ ∩ S- = ∅ heißt Entscheidungsproblem.
4/2, Folie 4
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Effizient lösbare Entscheidungsprobleme
Ein Entscheidungsproblem (S+,S-) mit S+,S- ⊆ { 0,1 }* heißt effizient lösbar,
wenn es einen Algorithmus A und ein Polynom p(.) gibt, so daß für alle
x ∈ S+ ∪ S- gilt:
•
•
•
falls x ∈ S+ gilt, so gibt A die Zahl 1 aus und stoppt
falls x ∈ S- gilt, so gibt A die Zahl 0 aus und stoppt
die Rechenzeit von A bei Eingabe x ist kleiner gleich p(|x|)
... A kann man auf einer deterministischen Turing-Maschine
implementieren, die nur polynomielle Rechenzeit benötigt
 Komplexitätsklasse P
Die Klasse P enthält alle Entscheidungsprobleme (S+,S-) mit S+,S- ⊆ { 0,1 }*,
die effizient lösbar sind.
4/2, Folie 5
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 ... auf dem Weg zur Definition der Klasse NP
Ein Algorithmus V heißt Beweissystem für das Entscheidungsproblem (S+,S-)
mit S+,S- ⊆ { 0,1 }*, falls für alle x ∈ S+ ∪ S- und alle y ∈ { 0,1 }* gilt:
•
•
•
bei Eingabe x, y gibt V eine der Zahlen 0 oder 1 aus und stoppt
wenn x ∈ S- gilt, so gibt V die Zahl 0 aus und stoppt
(/* Korrektheit des Beweissystems V */)
wenn x ∈ S+ gilt, so gibt es ein y‘∈ { 0,1 }*, so daß V bei Eingabe
von x, y‘ die Zahl 1 ausgibt und stoppt
(/* Vollständigkeit des Beweissystems V */)
... y‘ ein Beweis (/* eine Zeuge */) dafür, daß x ∈ S+ gilt
4/2, Folie 6
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Beispiele
Nicht-Primzahl-Problem
•
•
gegeben:
gefragt:
natürliche Zahlen x > 1
gibt es eine Zahl y mit 1 < y < x, die x teilt
Erfüllbarkeits-Problem
•
•
4/2, Folie 7
gegeben:
gefragt:
© 2008 Prof. Steffen Lange
eine aussagenlogischen Formel F
gibt es eine Belegung β der Variablen in F,
die die Formel erfüllt (/* wahr macht */)
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Nicht-Primzahl-Problem
•
•
•
S sei die Menge aller natürlichen Zahlen größer oder gleich 2
S+ sei die Teilmenge aller Nicht-Primzahlen
S- sei die Teilmenge aller Primzahlen
•
(S+,S-) sei das interessierende Entscheidungsproblem
•
V sei ein Algorithmus, der bei Eingabe zweier Zahlen x, y ∈ S mit y < x
die Zahl 1 ausgibt, wenn die Zahl y die Zahl x teilt, und sonst die Zahl 0
ausgibt
... offenbar ist V ein Beweissystem für (S+,S-)
... wenn die Zahl y die Zahl x teilt, ist y ein Zeuge dafür,
daß x eine Nicht-Primzahl ist
4/2, Folie 8
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Erfüllbarkeits-Problem
•
•
•
S sei die Menge aller aussagenlogischen Formeln
S+ sei die Menge aller erfüllbaren aussagenlogischen Formeln
S- sei die Menge aller unerfüllbaren aussagenlogischen Formeln
•
(S+,S-) sei das interessierende Entscheidungsproblem
•
V sei ein Algorithmus, der bei Eingabe einer Formel F ∈ S und einer
Belegung β der Variablen in F die Zahl 1 ausgibt, wenn die Belegung β
die Formel F erfüllt, und sonst die Zahl 0 ausgibt
... offenbar ist V ein Beweissystem für (S+,S-)
... wenn β die Formel F erfüllt, so ist β eine Zeuge dafür,
daß F erfüllbar ist
4/2, Folie 9
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Entscheidungsprobleme mit effizienten Beweissystemen
Ein Algorithmus V heißt effizientes Beweissystem für das Entscheidungsproblem (S+,S-) mit S+,S- ⊆ { 0,1 }*, falls V ein Beweissystem für das
Entscheidungsproblem (S+,S-) ist und es Polynome p(.) und q(.) gibt, so
daß für alle x ∈ S+ ∪ S- und alle y ∈ { 0,1 }* gilt:
•
•
wenn x ∈ S+ gilt, so gibt es ein y‘∈ { 0,1 }* mit |y‘| ≤ q(|x|), so daß
V bei Eingabe von x, y‘ die Zahl 1 ausgibt und stoppt
die Rechenzeit von V bei Eingabe x, y ist kleiner gleich p(|x|)
... y‘ ein hinreichend kurzer Beweis (/* eine Zeuge */) dafür, daß x ∈ S+ gilt
... ob ein y ein Beweis (/* eine Zeuge */) dafür ist, daß x ∈ S+ gilt, kann
effizient überprüft werden
... V kann man auf einer deterministischen Turing-Maschine implementieren,
die nur polynomielle Rechenzeit benötigt
4/2, Folie 10
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Nicht-Primzahl-Problem
•
•
•
S sei die Menge aller natürlichen Zahlen größer oder gleich 2
S+ sei die Teilmenge aller Nicht-Primzahlen
S- sei die Teilmenge aller Primzahlen
•
(S+,S-) sei das interessierende Entscheidungsproblem
•
V sei ein Algorithmus, der bei Eingabe zweier Zahlen x, y ∈ S mit y < x
die Zahl 1 ausgibt, wenn die Zahl y die Zahl x teilt, und sonst die Zahl 0
ausgibt
... V ist ein polynomieller Algorithmus
... wenn die Zahl y die Zahl x teilt, muß |y| ≤ |x| gelten
4/2, Folie 11
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Erfüllbarkeits-Problem
•
•
•
S sei die Menge aller aussagenlogischen Formeln
S+ sei die Menge aller erfüllbaren aussagenlogischen Formeln
S- sei die Menge aller unerfüllbaren aussagenlogischen Formeln
•
(S+,S-) sei das interessierende Entscheidungsproblem
•
V sei ein Algorithmus, der bei Eingabe einer Formel F ∈ S und einer
Belegung β der Variablen in F die Zahl 1 ausgibt, wenn die Belegung β
die Formel F erfüllt, und sonst die Zahl 0 ausgibt
... V ist ein polynomieller Algorithmus
... für jede Belegung β gilt: |β| ≤ |F|
4/2, Folie 12
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Komplexitätsklasse NP
Die Klasse NP enthält alle Entscheidungsprobleme (S+,S-) mit S+,S- ⊆ { 0,1 }*,
für die es ein effizientes Beweissystem V für (S+,S-) gibt.
 Beziehung zu Nicht-deterministischen Turing-Maschinen
•
•
4/2, Folie 13
bei Eingabe von x ∈ S+ ∪ S- wird zunächst ein y ∈ { 0,1 }* mit |y| ≤ q(x)
geraten
danach wird auf der Eingabe x, y eine deterministische Turing-Maschine
gestartet, die V implementiert
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
effizient lösbare
Entscheidungsprobleme
(/* die Komplexitätsklasse P */)
Entscheidungsprobleme mit effizienten
Beweissystemen
(/* die Komplexitätsklasse NP */)
... die Frage, ob P = NP gilt, ist äquivalent zur Frage, ob es schwieriger ist einen
Beweis zu finden oder zu überprüfen, ob ein Beweis korrekt ist
4/2, Folie 14
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik
Kapitel 4: Komplexitätstheorie
Das P=NP? Problem
 Vermutung: Es gilt P ≠ NP.
... wer diese Vermutung bestätigen oder widerlegen kann, ist ein gemachter Mann
 unterstützende Argumente
... es ist intuitiv klar, daß es schwieriger ist, eine Lösung zu finden als zu überprüfen,
ob ein Lösungskandidat eine Lösung ist
... es ist intuitiv klar, daß es schwieriger ist, einen Beweis zu finden als zu überprüfen,
ob ein Beweis korrekt ist
... es gibt tausende Probleme (/* Such- bzw. Entscheidungsprobleme */), von denen
man weiß, daß sie zur Komplexitätsklasse NP gehören und für die man trotz heftigen
Bemühens bisher keinen effizienten Lösungsalgorithmus gefunden hat
4/2, Folie 15
© 2008 Prof. Steffen Lange
-
HDa/FbI
-
Grundlagen der Theoretischen Informatik