Kapitel 5: Paradigmen des Algorithmenentwurfs Gliederung 1

Kapitel 5: Paradigmen des Algorithmenentwurfs
Gliederung
1.  Grundlagen
2.  Analyse der Laufzeit von Algorithmen
3.  Untere Schranken für algorithmische Probleme
4.  Sortier- und Selektionsverfahren
5.  Paradigmen des Algorithmenentwurfs
6.  Ausgewählte Datenstrukturen
7.  Algorithmische Geometrie
8.  Umgang mit algorithmisch schwierigen Problemen
• 
• 
• 
5/2, Folie 1
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Divide and Conquer
Dynamisches Programmieren
Greedy-Algorithmen
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Gliederung
u  Fahrplan (/* Dynamisches Programmieren */)
• 
• 
• 
ein kleines Beispiel
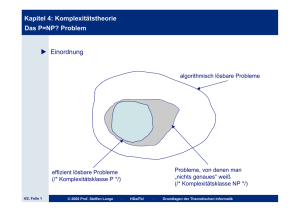
Einordnung
komplexere Beispiele
... im Mittelpunkt steht die Frage, wie man rekursive
Lösungsalgorithmen möglichst effizient implementiert
5/2, Folie 2
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Bionomialkoeffizient
• 
• 
Anzahl der Möglichkeiten, einer Menge von n Elementen genau
k Elemente auszuwählen (/* Bez.: bk(n,k) */)
offenbar muss n ≥ k gelten
u  Beispiel
• 
es sei M = { A,B,C,D,E } und uns interessiert bk(5,3)
{ A,B,C }
{ A,B,D }
{ A,B,E }
{ A,C,D }
{ A,C,E }
{ A,D,E }
5/2, Folie 3
© 2014 Prof. Steffen Lange
{ B,C,D }
{ B,C,E }
{ B,D,E }
{ C,D,E }
... also gilt: bk(5,3) = 10
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Definition des Bionomialkoeffizienten (/* Idee */)
{ A,B,C }
{ A,B,D }
{ A,B,E }
{ A,C,D }
{ A,C,E }
{ A,D,E }
{ B,C,D }
{ B,C,E }
{ B,D,E }
{ C,D,E }
... alle Teilmengen der
Größe 3 von { A,B,C,D,E }
{ B,C,D }
{ B,C,E }
{ B,D,E }
{ B,C }
{ B,D }
{ B,E }
{ C,D }
{ C,E }
{ D,E }
5/2, Folie 4
... alle Teilmengen der
Größe 2 von { B,C,D,E }
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
{ C,D,E }
... alle Teilmengen der
Größe 3 von { B,C,D,E }
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Definition des Bionomialkoeffizienten
• 
• 
Anzahl der Möglichkeiten, k Elemente aus einer Menge von n Elementen
auszuwählen (/* Bez.: bk(n,k) */)
es seien n, k ∈ N mit n ≥ k
Fall 1: n = k oder k = 0
• 
dann ist bk(n,k) = 1
Fall 2 : n > k > 0
• 
5/2, Folie 5
© 2014 Prof. Steffen Lange
dann ist bk(n,k) = bk(n-1,k-1) + bk(n-1,k)
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  ... erste rekursive Implementierung
int bk ( int n, int k ) {
int result;
if ( n == k || k == 0 ) result = 1;
else result = bk(n-1,k-1) + bk(n-1,k);
return (result);
}
5/2, Folie 6
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Beispiel (/* Berechnung von bk(4,2) */)
bk(4,2)
bk(3,1)
bk(2,0)
bk(3,2)
bk(2,1)
bk(1,0)
• 
• 
bk(2,1)
bk(1,1)
bk(1,0)
bk(2,2)
bk(1,1)
Blätter haben gemäß der Basisfälle den Wert 1
Wert eines inneren Knotens ergibt sich als Summe der Werte seiner Söhne
•  Wert eines Knotens k ist gleich der Anzahl der Blätter im Teilbaum
mit Wurzel k
•  Anzahl der Additionen gleich der Anzahl der inneren Knoten
5/2, Folie 7
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Analyse (/* erste rekursive Implementierung */)
• 
• 
es seien n, k ∈ N mit n ≥ k
es bezeichne T(A,n,k) die Anzahl der Additionen, die benötigt werden,
um bk(n,k) rekursiv zu berechnen
• 
• 
Anzahl der Blätter: bk(n,k)
Anzahl der inneren Knoten: bk(n,k) - 1
T(A,n,k) = bk(n,k) - 1
... für k = n/2 gilt: bk(n,k) - 1 ≥ 2n/2
... Anzahl der Additionen ist im „worst case“ exponentiell in n
5/2, Folie 8
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Anmerkungen
• 
im zur Berechnung von bk(n,k) gehörenden Berechnungsbaum gibt es
exponentiell viele Knoten (/* jeder Knoten entspricht einem Aufruf der
Funktion bk(.,.) */)
• 
da es für gegebene n und k mit n ≥ k nur (n+1)*(k+1) viele Paare (n‘,k‘)
mit n‘ ≤ n und k‘ ≤ k gibt, muss die Funktion bk(.,.) mehrfach mit
denselben Parametern aufgerufen werden
... Ausweg: man merkt sich die Ergebnisse der bereits
ausgeführten Funktionsaufrufe
5/2, Folie 9
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Beispiel
1 bk(4,2)
2 bk(3,1)
3 bk(2,0)
7 bk(3,2)
4 bk(2,1)
5 bk(1,0)
8
bk(2,1)
9 bk(2,2)
bk(1,1) 6
... die Zahlen geben an, in welcher Reihenfolge die
Funktionsaufrufe stattfinden
5/2, Folie 10
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  ... bessere rekursive Implementierung
• 
erzeuge ein zweidimensionales Array a der Größe (n+1) × (k+1) und
initialisiere jede Zelle des Arrays mit dem Wert „-1“ (/* für „unbekannt“ */)
int bk ( int n, int k ) {
int result;
if ( a[n][k] != -1 ) result = a[n][k];
else { if ( n == k || k == 0 ) result = 1;
else result = bk(n-1,k-1) + bk(n-1,k);
a[n][k] = result;
}
return (result);
}
5/2, Folie 11
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Analyse (/* bessere rekursive Implementierung */)
• 
• 
es seien n, k ∈ N mit n ≥ k
es bezeichne T‘(A,n,k) die Anzahl der Additionen, die benötigt werden,
um bk(n,k) auf diese Art rekursiv zu berechnen
• 
offenbar wird nur dann eine Addition ausgeführt, wenn im Array a in
der Zelle a[n‘][k‘] noch der Wert „-1“ steht und n‘ ≠ k sowie k‘ ≠ 0 gilt
T‘(A,n,k) ≤ (n+1)*(k+1) - (n+1) - k = n*k
... Anzahl der Additionen ist polynomiell in n statt exponentiell in n
5/2, Folie 12
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Anmerkungen
• 
da Funktionsaufrufe bei der Berechnung einen nicht unerheblichen
„Overhead“ verursachen, ist es vorteilhaft anstelle des zuletzt
verwendeten „top-down“-Ansatzes einen „bottom-up“-Ansatz zu wählen
... das nennt man dann üblicherweise „dynamische Programmierung“
5/2, Folie 13
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Implementierung mit Hilfe der dynamischen Programmierung
• 
erzeuge ein zweidimensionales Array a der Größe (n+1) × (k+1), wobei für
die Indizierung der Zeilen die Zahlen 0 bis n und für die Indizierung der
Spalten die Zahlen 0 bis k verwendet werden (/* der gesuchte
Binomialkoeffizient bk(n,k) steht dann in der Zelle a[n][k] */)
• 
fülle dieses Array gemäß der folgenden Regeln zeilenweise von links nach
rechts, d.h. es wird mit der Zelle a[0][0] begonnen
•  wenn i < j gilt, so setze a[i][j] = 0
•  wenn i = j oder j = 0 gilt, so setze a[i][j] = 1
•  andernfalls, setze a[i][j] = a[i-1][j-1] + a[i-1][j]
... offenbar genügen so O(n*k) viele Elementaroperationen, um den
Binomialkoeffizienten bk(n,k) zu bestimmen
5/2, Folie 14
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Beispiel
i=0
j=0
j=1
j=2
1
0
0
i=1
i=2
i=3
i=4
5/2, Folie 15
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Beispiel (cont.)
j=0
j=1
j=2
i=0
1
0
0
i=1
1
1
0
i=2
i=3
i=4
5/2, Folie 16
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Beispiel (cont.)
j=0
j=1
j=2
i=0
1
0
0
i=1
1
1
0
i=2
1
2
1
i=3
i=4
5/2, Folie 17
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Ein erstes Beispiel
u  Beispiel (cont.)
5/2, Folie 18
j=0
j=1
j=2
i=0
1
0
0
i=1
1
1
0
i=2
1
2
1
i=3
1
3
3
i=4
1
4
6
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Einordnung
u  ... „Situationsbeschreibung“
• 
es sei ein rekursiver Lösungsalgorithmus A gegeben, also ein
Algorithmus, der ...
• 
• 
• 
• 
das Gesamtproblem in Teilprobleme zerlegt
diese Teilprobleme rekursiv löst
aus den Lösungen der Teilprobleme die Lösung des
Gesamtproblems konstruiert
während der Verarbeitung einer Eingabe werden bestimmte
Teilprobleme mehrfach gelöst
u  Anmerkung
• 
5/2, Folie 19
es geht also nicht um „Divide-and-Conquer“-Algorithmen (/* hier zerlegt
man das Gesamtproblem im allgemeinen in disjunkte Teilprobleme und
es werden immer unterschiedliche Teilprobleme gelöst */)
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Einordnung
u  Grundidee (/* „top-down“-Variante */)
• 
• 
man löst das Gesamtproblem rekursiv und merkt sich „parallel“ die
Lösungen aller bereits vollständig bearbeiteten Teilprobleme
sobald ein weiteres Teilproblem rekursive gelöst werden soll, wird
überprüft, ob die Lösung für dieses Teilproblem bereits bekannt ist
• 
5/2, Folie 20
ist die Lösung bereits bekannt, muss das Teilproblem nicht
rekursiv gelöst werden
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Einordnung
u  Grundidee (/* „bottom-up“-Variante */)
• 
• 
man bestimmt die Menge M aller Teilprobleme, die überhaupt bei der
Lösung des Gesamtproblems eine Rolle spielen können
man wählt eine Anordnung der Teilprobleme in der Menge M, so dass
für jedes Teilproblem TP gilt:
• 
• 
5/2, Folie 21
alle Teilprobleme TP‘, die bei der rekursiven Lösung des
Teilproblems TP eine Rolle spielen, stehen in der gewählten
Anordnung vor TP
man löst sukzessive alle Teilprobleme in der Menge M, wobei man die
gewählte Anordnung respektiert, d.h. mit dem ersten Teilproblem
beginnt
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Einordnung
u  Beispiel (/* Fibonacci-Zahlen */)
• 
rekursive Definition der Fibonacci-Zahlen
• 
• 
• 
• 
um fib(n) zu bestimmen, sind höchstens die folgende Teilprobleme zu
lösen:
• 
• 
bestimme fib(m) für alle m ≤ n
geeignete Anordnung der Teilprobleme:
• 
5/2, Folie 22
fib(n) = 0, falls n = 0
fib(n) = 1, falls n = 1
fib(n) = fib(n-1) + fib(n-2), sonst
fib(0), fib(1), ..., fib(n-2), fib(n-1), fib(n)
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Einordnung
u  Anmerkungen
• 
im allgemeinen ist es nicht schwierig, an Hand des gegebenen rekursiven
Lösungsalgorithmus
• 
• 
• 
die Menge M der überhaupt zu lösenden Teilprobleme zu bestimmen
eine geeignete Anordnung der Teilprobleme in der Menge M zu
bestimmen
um die Laufzeit des nicht-rekursiven Lösungsalgorithmus für Eingaben der
Größe n abschätzen, wählt man eine Funktion T(n) = f(n)*g(n), wobei gilt:
• 
• 
5/2, Folie 23
f(n) ist eine asymptotische obere Schranke für die Anzahl der
Teilprobleme in der Menge M
g(n) ist eine asymptotische obere Schranke für den Aufwand,
um die Lösungen von Teilprobleme direkt zu bestimmen bzw.
aus bereits gelösten Teilproblemen zu konstruieren
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Einordnung
u  Anwendungsgebiet
• 
Lösung von Optimierungsproblemen
u  Optimierungsprobleme
• 
• 
• 
• 
Beschreibung einer Menge X zulässiger Eingaben
Beschreibung einer Menge Y zulässiger Ausgaben
Beschreibung einer Funktion, die jeder zulässigen Eingabe die nicht
leere Menge der korrekten Ausgaben zuordnet
Beschreibung einer Funktion, die jeder korrekten Ausgabe ihren Wert
(/* Güte, Kosten */) zuordnet
... das Ziel besteht darin, einer zulässigen Eingabe x eine korrekte
Ausgabe y zuzuordnen, die unter allen korrekten Ausgaben die
beste Güte bzw. die minimalen Kosten hat
5/2, Folie 24
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik
Kapitel 5: Paradigmen des Algorithmenentwurfs
Weiterer Fahrplan
u  Gegenstand
• 
wir werden uns ein paar typische Optimierungsprobleme anschauen,
die man effizient mit Algorithmen lösen kann, die auf dem Paradigma
der dynamischen Programmierung basieren
• 
konkrete Optimierungsprobleme und die zugehörigen nicht-rekursiven
Lösungsalgorithmen
• 
der Entwurf der nicht-rekursiven Lösungsalgorithmen anhand gegebener
rekursiver Lösungsalgorithmen
• 
der Entwurf von rekursiven Lösungsalgorithmen
u  Fokus
5/2, Folie 25
© 2014 Prof. Steffen Lange
-
HDa/FbI
-
Algorithmik