rutherford atomhülle

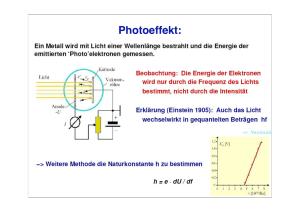
Vorlesung Physik für Pharmazeuten
PPh - 11
Optik &Atomphysik
09.07.2007
und
16.07.2007
Der Hertzsche Dipol
Der Hertzér Original Aufbau
Höchste Frequenzen lassen sich bei kleinsten Werten von L und C erzielen.
Reduktion des Schwingkreises zum Stab -> Hertz’scher Dipol
Versuch Dipolstrahlung
Licht als Welle
Polarisation (transversale Welle)
Interferenz (Überlagerung von Wellen)
Beugung (Huygenssches Prinzip)
Spektrum elektromagnetischer Wellen:
Versuch Lichtgeschwindigkeit
Polarisation
Ein senkrecht zum Sendedipol ausgerichteter Empfangsdipol nimmt keine
Strahlungsenergie auf. Die Strahlung ist polarisiert.
Polarisationsrichtung
des Lichts
Orientierung
des Polarisators.
E
B
ϕ
Die Transmission der EM Welle hängt vom
Polarisationswinkel ϕ ab.
el. Feldvektor
Intensität:
ET = E 0 ⋅ cos(ϕ )
IT = I0 ⋅ cos (ϕ )
2
Mikrowellen-Polarisatoren
Michaelson-Interferometer
Huygens-Fresnel'sches Prinzip
Jeder von einer Welle erregte Punkt wird selbst zum
Ausgangspunkt einer neuen Kreis-/Kugelwelle.
Gitterspektrometer
2d sin ϑ = mλ
m = 1,2,...
λ
= m⋅ N
∆λ
N : Anzahl Gitterstreifen
m : Ordnung
Anwendung: Gitterspektrometer
Benzol
Auflösung eines Gitterspektrometers:
Wann kann man 2 Peaks noch voneinander trennen?
Xylol
Beugung an einer kreisrunden Öffnung
ϕ
D
Lage des ersten
Beugungsminimums
ϕ min = 1,22 ⋅
λ
D
Auflösungsbegrenzung durch
Beugung:
Für zwei selbstleuchtende Objekte ist
der kleinste auflösbare Abstand ∆x :
∆xmin
0.61⋅ λ
=
n ⋅ sin α
Wobei λ die Wellenlänge und
n sinα die numerische Apertur ist.
(α: Öffnungswinkel der Linse)
Röntgenstrahlung
beschleunigte Ladungen
elektromagnetische Strahlung
Interferenz von Röntgenstrahlen an Kristallen
Pulverdiffraktion
2
2
1
⎛h⎞ ⎛k ⎞ ⎛ l ⎞
=⎜ ⎟ +⎜ ⎟ +⎜ ⎟
d hkl ⎝ a ⎠ ⎝ b ⎠ ⎝ c ⎠
2
dhkl : Netzebenenabstand
h,k,l : Millersche Indizes
Röntgenstrukturanalyse
Röntgenlicht
Probe:
Proteinkristall
Berechnung
Strahlungsabsorption/ Beersches Gesetz
Licht transportiert Energie: Die Intensität I gibt die transportierte Energie pro
Zeit- und Flächeneinheit an. [W/m2]
In absorbierenden Medien wird die Lichtintensität abgeschwächt.
x
∆I = −α ⋅ I ⋅ ∆x
Iein
Iaus
I(x) = ?
dI
= −α ⋅ I
dx
I(x) = Ieine −α ⋅x
α: Extinktionskoeffizient [1/m]
In Lösungen ist α proportional der
Konzentration. (Spektrometer)
Wärmestrahlung
Definition:
Das Emissionsvermögen E eines Körpers ist die pro Flächeneinheit
abgestrahlte Leistung [W/m2].
Das Absorptionsvermögen A ist der Bruchteil der von einem Körper
absorbierten Strahlung (A=1, alle Leistung, die einfällt wird absorbiert,
‘schwarzer Körper’, A<1 ‘grauer Körper’)
2 Platten im Temperaturgleichgewicht:
I
II
e
E
AI=1
AII<1
E
e=
AII
Kirchhoffsches Strahlungsgesetz:
Das Verhältnis von Emissions- zu
Absorptions-vermögen ist für alle Körper
gleich und zwar dem Emissionvermögen e
eines schwarzen Strahlers.
Wärmestrahlung - Plancksches Strahlungsgesetz:
Wärmestrahlung - Plancksches
Strahlungsgesetz:
P = A⋅σ ⋅ T
4
−8
σ = 5,67 ⋅10
W
2 4
m K
σ: Stefan-Boltzmann Konstante
Die kosmische Hintergrundstrahlung:
Das Echo des Urknalls
Photoeffekt:
Wellen- und Photonencharakter:
Wellencharakter massiver Teilchen:
Materiewellen
- Es ist eine Grundeigenschaft von Materie, daß sie sowohl Wellen- als auch
Teilcheneigenschaften besitzt.
- Nach de Broglie ist die Wellenlänge eines Teilchens gegeben durch:
h
λ=
p
de Broglie Wellenlänge
p: Impuls des Teilchens
h: Plancksches Wirkungsquantum = 6,6*10-34 Js
Elektronenbeugung
an Lochblende
Elektronen Mikroskop
λ=
h
h
=
p mv
(de Broglie Beziehung)
Elektronenbeschleunigung
1
2
mv 2 = e ⋅ U
2e ⋅ U
v=
me
1.23
λ [nm] =
U [V ]
z.B. 100keV
λ~3pm
Die Wellenfunktion von Teilchen
Die Aufenthaltswahrscheinlichkeitsdichte eines Teilchens
ist gleich dem Betragsquadrat seiner normierten
Wellenfunktion:
2
P( x) = Ψnorm = Ψ *Ψ
Ausbreitung eines Wellenpakets
Wellencharakter massiver Teilchen:
Der Tunneleffekt
Das Linienspektrum von Wasserstoff
n2
λ = 364,6nm ⋅ 2
n −1
Balmerserie
n=1,2,3...
Termschema
Spezialfall von der Rydberg-Ritz Formel
⎛1 1⎞
= R ⋅ Z ⋅ ⎜⎜ − ⎟⎟
λ
⎝ na ne ⎠
1
E photon
R=10,9µm-1
Rydberg-Konstante
2
⎛1 1⎞
= h ⋅ν = Rhc ⋅ Z ⋅ ⎜⎜ − ⎟⎟
⎝ na ne ⎠
2
Rutherford'sches Streuexperiment
• Der Radius des Atomkerns: 10-15 m (= 1 Femtometer = 1 fm)
• Vgl. Radius der Atomhülle: 10-10 m (0.1 nm)
Thomson Modell
Rutherford Modell
Der e/m Versuch von Thomson
Fadenstrahlrohr
(Wehnelt-Rohr)
U: Beschleunigungsspannung
Ablenkung im elektr. Feld
Ablenkung im Magnetfeld
Lorentzkraft=Zentripetalkraft
Kreisbahn mit :
e
2U
= 2 2
m r ⋅B
Thomson
me = 9.1·10-31 kg
Bohrschen Postulate
In einem Atom bewegt sich ein Elektron nach den
Gesetzen der klassischen Mechanik auf diskreten
Kreisbahnen mit Energien En. (Quantelung der Energie)
Die Bewegung des Elektrons erfolgt strahlungslos.
Beim Übergang des Elektrons von einem stationärem
Zustand mit Energie Ea in einen stationären Zustand
mit niedrigerer Energie Ee wird ein Photon der
Frequenz, v=(Ea-Ee)/h emittiert.
Der Drehimpuls eines Elektrons in einem stationären
Zustand nimmt nur die diskreten Werte an, wobei n eine
natürliche Zahl ist. (Quantelung des Drehimpulses)
nh
mvr =
= nh
2π
2π ⋅ rn = n ⋅ λe
mit mv=h/λ
hν
Ea
Eb
Das Bohrsche Atommodell erklärt die Linien des
Wasserstoff
1 m ⋅ e4
1
En = −
2
2
2 = −13,6 eV 2
8 ⋅ ε0 n ⋅ h
n
Der Franck-Hertz Versuch
Anregung des ersten Energieniveaus von Quecksilber durch Elektronen
e- Hg
e- eHg
Die Elektronen werden durch Va beschleunigt und nach
der Anode durch eine Gegenspannung abgebremst.
∆E = E1 − E0
hν =
hc
λ
= 4.9eV
Quantenphänomene : Welle-Teilchen Dualismus
Wellen zeigen Teilcheneigenschaften
Energie :
Impuls :
Eγ = h ⋅ν = hω
pγ = Eγ c
Teilchen zeigen Wellencharakter
E = h ⋅ν = mc 2
p=h λ
Drehimpuls : Lγ = h 2π
Einstein Gl.
De Broglie-Beziehung
In einem Experiment werden niemals Wellen- und Teilcheneigenschaften
gleichzeitig nachgewiesen.
Komplementaritätsprinzip (Niels Bohr 1927)
1
∆x ⋅ ∆p ≥ h
2
1
∆E ⋅ ∆t ≥ h
2
Heisenbergsche Unschärferelation :
Ionisierungsenergien
Energie die nötig ist das äußerste Elektron aus der
Atomhülle zu entfernen
Das Periodensystem
Das Wasserstoffatom
Anwendung der Schrödingergleichung auf das Wasserstoffproblem (Elektron
im Coulombfeld eines Protons)
Quantenzahlen des Wasserstoffatoms:
n=1,2,3...
l=0,1,2,...n-1
m=-l,-l+1,...+l
Termschema des Wasserstoff:
Bei Emission und Absorption
von Strahlung gilt die
Auswahlregel
∆l = ±1
Darstellung des
Bahndrehimpulses
Ψ
2
Elektronendichteverteilung
des Wasserstoffatoms
Grundzustand, n=1
Zustände n=2
Rutherford'sches Streuexperiment
• Der Radius des Atomkerns: 10-15 m (= 1 Femtometer = 1 fm)
• Vgl. Radius der Atomhülle: 10-10 m (0.1 nm)
Thomson Modell
Rutherford Modell
Atomkerne
p
n
p
n
4
Die Atomkerne bestehen aus
Z Protonen und N Neutronen,
zusammen aus A = Z + N 'Nukleonen'
Atomkern des 2 H
N>Z
A
ZX
"Nuklide"
A: Kernmassenzahl
Z: Kernladungszahl
Isotope : Nuklide mit Z=const.
N=Z
• Ladung des Neutrons = 0,
mn = 1.6750·10-27 kg
• Ladung des Protons = 1 Elementarladung,
Masse mp = 1.6723·10-27 kg
Bindungsenergien der Atomkerne
Äquivalenz von Masse und Energie
E = m ⋅ c2
(1u ) ⋅ c 2 = 931,5 MeV
Die Masse eines Kerns ist geringer als die Summe der Massen seiner Nukleonen
(ca. 1%).
mK < Z ⋅ m p + ( A − Z ) ⋅ mn
Der sog. “Massendefekt” ∆m steckt in der Bindungsenergie, EB.
mK ⋅ c 2 = Z ⋅ m p ⋅ c 2 + ( A − Z ) ⋅ mn ⋅ c 2 − EB
Mittlere Bindungsenergie pro Nukleon [MeV]
Kernspaltung und Kernfusion
Kernspaltungs-Reaktion
n + 235
92 U → X + Y + z ⋅ n + ∆E
1
0 th
Massenzahl A
Radioaktivität
Radioakive Kerne senden α−, β− und γ−Strahlung aus, welche
als ionisierende Strahlung im Geiger-Müller Zahlrohr
nachweisbar ist.
Natürliche Radioaktivität
Zerfallsreihe des Thoriums
weitere Zerfallsreihen :
Uran-Radium Reihe
Actinium Reihe
Neptunium Reihe („ausgestorben“)
α-Zerfall
A
Z
A-4
X
M
Z-2
XT