Blatt 2 - M10 - Technische Universität München

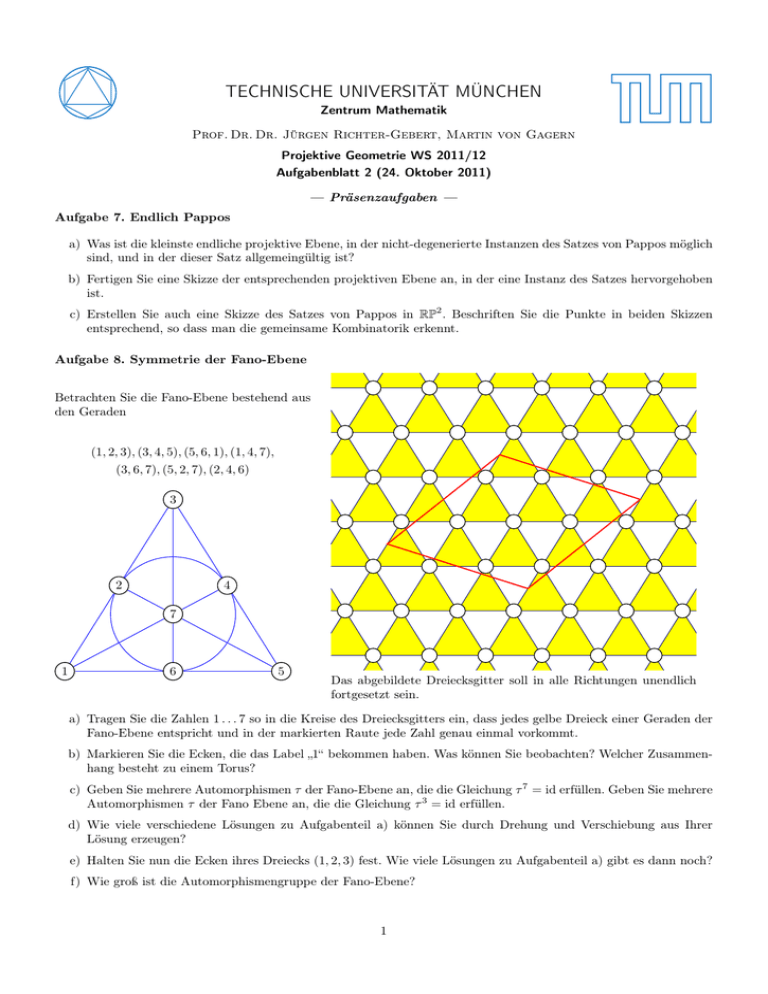
TECHNISCHE UNIVERSITÄT MÜNCHEN
Zentrum Mathematik
Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern
Projektive Geometrie WS 2011/12
Aufgabenblatt 2 (24. Oktober 2011)
— Präsenzaufgaben —
Aufgabe 7. Endlich Pappos
a) Was ist die kleinste endliche projektive Ebene, in der nicht-degenerierte Instanzen des Satzes von Pappos möglich
sind, und in der dieser Satz allgemeingültig ist?
b) Fertigen Sie eine Skizze der entsprechenden projektiven Ebene an, in der eine Instanz des Satzes hervorgehoben
ist.
c) Erstellen Sie auch eine Skizze des Satzes von Pappos in RP2 . Beschriften Sie die Punkte in beiden Skizzen
entsprechend, so dass man die gemeinsame Kombinatorik erkennt.
Aufgabe 8. Symmetrie der Fano-Ebene
Betrachten Sie die Fano-Ebene bestehend aus
den Geraden
(1, 2, 3), (3, 4, 5), (5, 6, 1), (1, 4, 7),
(3, 6, 7), (5, 2, 7), (2, 4, 6)
3
2
4
7
1
6
5
Das abgebildete Dreiecksgitter soll in alle Richtungen unendlich
fortgesetzt sein.
a) Tragen Sie die Zahlen 1 . . . 7 so in die Kreise des Dreiecksgitters ein, dass jedes gelbe Dreieck einer Geraden der
Fano-Ebene entspricht und in der markierten Raute jede Zahl genau einmal vorkommt.
b) Markieren Sie die Ecken, die das Label „1“ bekommen haben. Was können Sie beobachten? Welcher Zusammenhang besteht zu einem Torus?
c) Geben Sie mehrere Automorphismen τ der Fano-Ebene an, die die Gleichung τ 7 = id erfüllen. Geben Sie mehrere
Automorphismen τ der Fano Ebene an, die die Gleichung τ 3 = id erfüllen.
d) Wie viele verschiedene Lösungen zu Aufgabenteil a) können Sie durch Drehung und Verschiebung aus Ihrer
Lösung erzeugen?
e) Halten Sie nun die Ecken ihres Dreiecks (1, 2, 3) fest. Wie viele Lösungen zu Aufgabenteil a) gibt es dann noch?
f) Wie groß ist die Automorphismengruppe der Fano-Ebene?
1
Aufgabe 9. 93 -Konfigurationen
Eine (nr , nr )-Konfiguration wird auch abkürzend als nr -Konfiguration bezeichnet. Hier sehen Sie einige Abbildungen
von 93 -Konfigurationen.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
a) Bestimmen Sie, welche dieser Abbildungen isomorphe Inzidenzstrukturen darstellen. Beschriften Sie die Punkte
so, dass bei isomorphen Konfigurationen die Namen aller kollinearen Punktetripel übereinstimmen, damit man
die Isomorphie leicht erkennt. Die meisten der folgenden Teilaufgaben können für alle zueinander isomorphen
Konfigurationen gleichzeitig bearbeitet werden.
b) Bestimmen Sie zu jeder Konfiguration die duale Inzidenzstruktur, und ermitteln Sie, zu welchen der dargestellten primalen Inzidenzstrukturen diese isomorph ist. Belegen Sie diese Isomorphie wieder durch eine geeignete
Beschriftung der ursprünglichen Geraden.
c) Im Rahmen dieser Aufgabe nennen wir zwei Punkte P und Q einer Konfiguration isotop zueinander, wenn es
einen Automorphismus der Konfiguration gibt, der P auf Q abbildet. Die so definierte Isotopierelation ist eine
Äquivalenzrelation. Bestimmen Sie für jede abgebildete Konfiguration die Klassen isotoper Punkte.
Hd) Konstruieren Sie weitere 93 -Konfigurationen, und untersuchen Sie, zu welchen der abgebildeten Konfigurationen
diese isomorph sind.
2
— Hausaufgaben —
Aufgabe 10. Kollineationen
Gegeben seien die folgenden Punkte in CP2 :
 
1
A = 0
0
 
0
B = 1
0
 
0
C = 0
1
 
1
D = 1
1
 
1
D0 =  i 
1
a) Finden Sie eine projektive Abbildung, die die Punkte A, B und C fix lässt und den Punkt D auf D0 abbildet.
Geben Sie eine Funktion τa : P → P an, die den Effekt dieser Abbildung auf die Punkte der Ebene beschreibt.
b) Finden Sie eine Kollineation, die keine projektive Abbildung ist, aber dennoch die vier Punkte wie eben angegeben
abbildet. Beschreiben Sie auch diese als Funktion τb : P → P
c) Wenden Sie die beiden in den vorherigen Teilaufgaben ermittelten Kollineationen auf den Punkt E = (i, 0, 1)T
an, und vergleichen Sie die Ergebnisse.
d) Weisen Sie nach, dass die Abbildung τb wohldefiniert ist.
Aufgabe 11. Moulton-Ebene
Die sogenannte Moulton-Ebene ist eine affine Ebene, in der der Satz von Desargues nicht gilt. Ihr projektiver
Abschluss lässt sich wie folgt beschreiben:
P = PR
L = LR
   
(
x
a
y  I  b  ⇔ 2ax + by + cz = 0
1ax + by + cz = 0
z
c
falls x · z > 0 und a · b > 0
sonst
a) Überprüfen Sie, dass die Sonderbehandlung in der Inzidenzrelation I nur endliche Punkte rechts der y-Achse
sowie endliche Geraden mit endlicher negativer Steigung betrifft.
b) Zeigen Sie, dass die Inzidenzrelation wohldefiniert ist.
c) Machen Sie sich ein anschauliches Bild dieser Ebene.
d) Formulieren Sie Verfahren, wie Sie Verbindungsgeraden und Schnittpunkte bestimmen können.
e) Argumentieren Sie, dass diese projektive Moulton-Ebene alle Axiome für eine projektive Ebene erfüllt.
f) Fertigen Sie eine Konstruktion an, die belegt, dass der Satz von Pappos in dieser Ebene nicht allgemeingültig
ist.
g) Fertigen Sie eine Konstruktion an, die belegt, dass der Satz von Desargues in dieser Ebene nicht allgemeingültig
ist.
3