Zusammenfassung

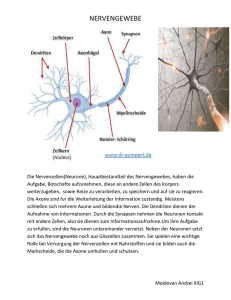
Waves in Excitable Media
Samuel Voit
9. Mai 2006
Die Nervenzelle Nervenzellen, auch bekannt als Neuronen, sind in der Lage elektrische Impulse (Aktionspotentiale) zu verarbeiten und an weitere Nervenzellen weiterzureichen. Für die Informationsverarbeitung in Lebewesen wie z.B. Vertebraten sind sie essentiell. Neuronen sind in der Lage Aktionspotentiale
mit einer Leitungsgeschwindigkeit von bis zu 100 m/s zu übertragen.
Bildquelle: http://www.anselm.edu/homepage/jpitocch/genbio/actpot.jpg
Die Funktionsweise eines Neurons hängt in komplizierter Weise von verschiedenen Ionen und deren
Konzentrationen im Neuron resp. in seiner Umgebung ab. Bei einer genügenden Depolarisation des Neurons öffnen sich in kürzester Zeit N a+ -Kanäle in der Zellmembran, womit für N a+ -Ionen einen Fluss
entlang ihres Konzentrationsgradienten ermöglicht wird. Gleichzeitig öffnen sich, langsamer als die N a+ Kanäle, K + -Ionenkanäle, welche ihrerseits einen Fluss von K + -Ionen (aus der Zelle heraus) erlauben, der
dem der N a+ -Ionen entgegenwirkt. Die N a+ -Ionenkanäle inaktivieren und schliessen sich spontan nach
kurzer Zeit, die K + -Kanäle jedoch erst nachdem die Spannung wieder auf ihren ursprünglichen Wert
(Ruhepotential) zurückgekehrt ist. Das Aktionspotential (Hyperpolation) wird also durch die spontane
Inaktivierung der N a+ -Kanäle und durch den K + -Ionenfluss langsam abgebaut und in die Nähe des
Ruhepotentials zurückgebracht. Dort gehen die N a+ -Kanäle zudem wieder in eine aktivierbare Form
über.
Hodgkin-Huxley und FitzHugh-Nagumo Modell
Hodgkin-Huxley Modell (1952) mit C Kapazität Zellmembran, mit VN a , VK und VL
Gleichgewichtspotentiale und mit gN a , gK und gL Durchlässigkeiten der Membran für die
verschiedenen Ionen:
C
dV
= −gN a m3 h(V − VN a ) − gK n4 (V − VK ) − gL (V − VL ) + Ia ,
dT
dm
= αm (V )(1 − m) − βm (V )m,
dt
dn
= αn (V )(1 − n) − βn (V )n,
dt
dh
= αh (V )(1 − h) − βh (V )h
dt
1
FutzHugh-Nagumo Modell mit v als schnelle Variabel und mit w als langsame Variabel:
dv
= f (v) − w + Ia ,
dt
dw
= bv − γw,
dt
f (v) = v(a − v)(v − 1),
0 < a < 1, γ > 0, b > 0
Travelling Wave
d.h. Ia = 0):
Das FHN(FitzHugh-Nagumo)-System (mit Diffusion und ohne zugeführten Strom,
dv
= f (v) − w + Duxx ,
dt
dw
= bv − γw,
dt
f (v) = v(a − v)(v − 1),
0 < a < 1, γ > 0, b > 0
hat die TW-Lösung:
u = u(z),
z = x − ct,
1/2
D
c=
(1 − 2a),
2
d.h. die Geschwindigkeit der Welle ist positiv genau dann wenn a < 1/2 (Anm:
D = 1, b = γ = 0.002, a = 0.25, Euler explizit
2
R1
0
f (u)du > 0).