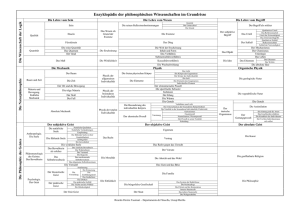
energieformen mechanik

PHYSIK KLASSE 11
MECHANIK 4
Dynamik 2: Arbeit, Energie, Leistung
2.5.7, 2015-2016
H. Knopf
Physik Klasse 11.2: Mechanik 4
Dieses Material ist ausschließlich für den unterrichtsbegleitenden Einsatz bestimmt. Dieses Dokument stellt keinen Ersatz für den Unterricht dar. Die Teilnahme an den Unterrichtsveranstaltungen ist zwingend erforderlich. Die Lektüre
der im Anhang angegebenen Literatur wird dringend empfohlen. Jede weitere
Nutzung – insbesondere Vervielfältigung jeglicher Art – bedarf der ausdrücklichen Zustimmung des Autors.
Wie jede Publikation ist auch diese nicht gänzlich frei von Fehlern. Die Benutzung erfolgt auf eigene Gefahr und ohne Gewähr für die Folgen.
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 2
Physik Klasse 11.2: Mechanik 4
4. KURSHALBJAHR 11.2: MECHANIK 4 – ARBEIT, ENERGIE, LEISTUNG ......................................... 4
4.1. ENERGIE, ARBEIT, LEISTUNG ...................................................................................................................... 4
4.1.1. Energie ............................................................................................................................................... 4
4.1.2. Arbeit ................................................................................................................................................. 6
4.1.2.1. Konstante Kraft bei gleicher Wirkungsrichtung von Kraft und Weg .......................................................... 6
4.1.2.2. Konstante Kraft bei ungleicher Wirkungsrichtung von Kraft und Weg ...................................................... 6
4.1.2.3. Veränderliche Kraft bei gleicher Wirkungsrichtung von Kraft und Weg .................................................... 7
4.1.2.4. Veränderliche Kraft bei ungleicher Wirkungsrichtung von Kraft und Weg ................................................ 9
4.1.3. Arbeit – Energie ............................................................................................................................... 10
4.1.4. Leistung ............................................................................................................................................ 18
4.2. REGISTER KURSHALBJAHR 11.2 : MECHANIK 4 – ARBEIT, ENERGIE, LEISTUNG ........................................ 20
4.3. VERZEICHNIS DER ABBILDUNGEN, TABELLEN, QUELLTEXTE UND DEFINITIONEN KURSHALBJAHR 11.2 :
MECHANIK 4 – ARBEIT, ENERGIE, LEISTUNG ................................................................................................... 21
4.4. QUELLEN KURSHALBJAHR 11.2 : MECHANIK 4 – ARBEIT, ENERGIE, LEISTUNG ........................................ 22
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 3
Physik Klasse 11.2: Mechanik 4
4. Kurshalbjahr 11.21: Mechanik 4 – Arbeit, Energie, Leistung
4.1. Energie, Arbeit, Leistung
4.1.1. Energie
Zu Beginn sollten wir – wieder einmal – zuerst klären, was wir unter bestimmten Begriffen verstehen wollen.
Die Antwort auf die Frage, was denn Energie sei, kann man kurz und bündig
keine Antwort geben. Die einzelnen Formen sind zu vielfältig und die Übergänge zwischen können sehr komplex werden.
Ein möglicher Versuch einer Definition könnte lauten:
Definition 1: Energie
Ein System, welches in der Lage ist mechanische Arbeit zu verrichten, Licht
oder Wärme abzugeben, besitzt Energie.
Auf jeden Fall beschreibt die Energie den Zustand eines Systems. Ändert sich
der Zustand des Systems, so ist das zumeist mit einer Veränderung der Energie
verbunden. Z.B. Ändert der Körper in der Abbildung 1 seine Höhe und beim
Fallen seine Temperatur. D.h. verändert seine Lageenergie und seine thermische
Energie.
Also sollten wir unsere Definition ergänzen:
Definition 2 Energie 2
Energie ist eine Zustandsgröße.
Abbildung 1
Höhe h1
Körper
Masse m,
Temperatur T1
Höhe h2
Körper
Masse m,
Temperatur T2
T1>T2
1
Nach RRL 2003.
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 4
Physik Klasse 11.2: Mechanik 4
Die Vielfalt der Formen hat lange Zeit verhindert, dass man eine wichtige Gesetzmäßigkeit nicht erkannte, den Satz von der Erhaltung der Energie.
Die Summe aller Energien in einem abgeschlossenen System, bleibt konstant.
Lediglich die Formen der Energie ändern sich.
Tabelle 1: Beispiele für Energieformen
Lageenergie (potentielle Energie)
Spannenergie einer Feder (potentielle Energie)
kinetische Energie
Wärme
innere Energie
chemische Energie
Kernenergie
Licht
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
Mechanik
Thermodynamik
Chemie
Quantenphysik
© H. Knopf
S. 5
Physik Klasse 11.2: Mechanik 4
4.1.2. Arbeit
Bei mechanischen Systemen spielt vor allem die Arbeit eine wichtige Rolle.
Definition 3: mechanische Arbeit
Wird ein Körper unter Krafteinwirkung verschoben oder verformt, so wird an
ihm Arbeit verrichtet.
4.1.2.1. Konstante Kraft bei gleicher Wirkungsrichtung von Kraft und Weg
Unter der Bedingung, dass Kraft und Weg eine Richtung haben und die Kraft
konstant über den Weg wirkt, so gilt:
Gleichung 1
W  Fs
Abbildung 2: Schleppen eines Tankers (1)
F
Wenn z.B. ein Schlepper einen Tanker schleppt, so
sind die Richtungen von Kraft und Weg gleich.
s
4.1.2.2. Konstante Kraft bei ungleicher Wirkungsrichtung von Kraft und Weg
Sollten die Richtungen nicht gleich sein, aber eine konstante Kraft wirken, so
gilt:
Gleichung 2: Skalarprodukt zur Berechnung der Arbeit
W  F s
Das Operationszeichen  bedeutet hier das Skalarprodukt zweier Vektoren.
D.h. während die beiden Faktoren zwar Vektoren
sind, so ist jedoch das Ergebnis eine skalare Größe.
Die Arbeit kann zwar zugeführt oder abgegeben
werden, jedoch hat sie selbst keine Richtung.
Abbildung 3: Schleppen eines Tankers (2)
Lauf Mathematik wird das Skalarprodukt wie folgt
berechnet:
F2
s
F1
Gleichung 3: Skalarprodukt zur Berechnung der Arbeit


W  F  s  cos  F , s  Fs  cos
Die Wirkungslinien der Kräfte bzw. die Richtung des Weges, der hier zurückgelegt wird, stimmen nicht überein, da die Schlepper in verschiedene Richtungen
ziehen.
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 6
Physik Klasse 11.2: Mechanik 4
4.1.2.3. Veränderliche Kraft bei gleicher Wirkungsrichtung von Kraft und Weg
Wenn die Kraft nicht konstant wirkt, wie z.B. beim Spannen einer Feder, so ist
es schwieriger die verrichtete Arbeit zu ermitteln.
Um ein brauchbares Ergebnis zu erhalten, holen wir uns eine kleine Anregung
bei unseren anderen Fällen.
Wenn die Kraft und der Weg gleichgerichtet sind, so gilt Gleichung 1 für konstante Kräfte.
Stellt man die Kraft, die über den Weg wirkt, grafisch dar, so erhält man Abbildung 4:
Abbildung 4
Die Fläche unter dem Graphen ist ein Rechteck und es gilt für seinen Flächeninhalt mit F  s . Das ist jedoch genau die Gleichung 1 für die geleistete Arbeit.
D.h. die Fläche unter dem Graphen im F-s-Diagramm entspricht der Arbeit.
Beim Spannen einer Feder gilt das Hookesche Gesetz. Graphisch dargestellt
ergibt sich
Abbildung 5: F-s-Diagramm für das Spannen einer Feder
Hier kann man den Flächeninhalt noch sehr elementar über eine Dreiecksfläche
berechnen. Für die Kraft FE am Ende gilt:
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 7
Physik Klasse 11.2: Mechanik 4
Gleichung 4: Federspannarbeit
W
1
FE  s
2
Sollte die Kraft sich etwas unregelmäßig ändern, wie z.B. in Abbildung 6, so
muss wieder die Integralrechnung benutzt werden.
Abbildung 6
Gleichung 5
sE
W   F s ds
sA
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 8
Physik Klasse 11.2: Mechanik 4
4.1.2.4. Veränderliche Kraft bei ungleicher Wirkungsrichtung von Kraft und Weg
Kommt jetzt noch eine Abweichung der Richtungen hinzu, so muss die Formel
in Gleichung 5 noch weiter verallgemeinert werden.
Gleichung 6: mechanische Arbeit
sE
W   F s  d s
sA
W
 F  cosF , s d s
sE
sA
W
sE
 F  cos  d s
sA
In der Regel wird man versuchen, die Formel auf die konkrete Situation anzupassen. Dadurch wird die Gleichung zumeist einfacher und man kann relativ
einfach das Problem lösen.
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 9
Physik Klasse 11.2: Mechanik 4
4.1.3. Arbeit – Energie
Wenn ein mechanisches System Energie verliert (besser gesagt an die Umgebung abgibt), so wird diese Energie in Arbeit umgewandelt oder wenn Arbeit an
einem System zugeführt wird, so nimmt dessen Energie zu usw.
Oft ist es erst durch die Beobachtung und Messung der mechanischen Arbeit
möglich, den Energiezustand eines Systems zu bestimmen.
Abbildung 7: Arbeit – Energie
Höhe h1
Höhe h1
Körper
Masse m
Hubarbeit
Beschleunigungsarbeit
Körper
Masse m
Höhe h2
Höhe h2
Körper
Masse m
Körper
Masse m
a) freier Fall
b) Heben
In dem Maße wie das System Arbeit umsetzt, verändert sich die Energie des
Systems.
Die Arbeit ist eine Prozessgröße, die die Veränderung der Energie eines Systems
beschreibt.
Da es sich bei der Arbeit und der Energie um verschiedene Größentypen handelt, darf man sie nicht gleichsetzen. Aber man kann ihre Beträge vergleichen.
Damit ergibt sich die Möglichkeit Formeln für die einzelnen Energieformen zu
finden indem man sie aus der Arbeit herleitet.
Im Weiteren soll die Methode an Beispielen demonstriert werden.
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 10
Physik Klasse 11.2: Mechanik 4
1. Beispiel: Heben eines Körpers
„Leiten Sie die Formel der Hubarbeit und der Lageenergie eines Körpers her,
wenn der Körper von der Höhe Null auf die Höhe h angehoben wird.“, so könnte
eine klassische Aufgabe in einer Klausur heißen.
Abbildung 8
Höhe h1
Hubarbeit
Körper
Masse m
FHub
s
FG
Höhe h2
Körper
Masse m
Allgemein gilt für die Arbeit:
Gleichung 7
sE
W   F s  d s
sA
W
 F  cosF , s d s
sE
sA
sE


W   F  cos  F , s ds
sA
Hier kann man, da  F , s  0 gilt, die Gleichung 7 vereinfachen
sE


W   F  cos  F , s ds
sA
sE
W   F  ds
sA
Für das Heben gilt FHub   FG und damit auch FHub  FG . Die Gewichtskraft kann
hier als konstant angenommen werden. Die Grenzen des Integrals ergeben sich
aus der Aufgabenstellung mit 0 bzw. h.
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 11
Physik Klasse 11.2: Mechanik 4
h
W   FG  ds
0
W  FG s 0
h
W  FG h
Gleichung 8: Hubarbeit
W  mgh
Für die Energie gilt:
W  E
W  E pot1  E pot 2
Die Lage des Ausgangsniveaus für die Lageenergie ist beliebig wählbar. Hier
nehmen wir in sinnvoller Weise an, dass der untere Punkt die Energie Null haben soll. Gesucht ist die Lageenergie eines Körpers in der Höhe h. Damit ergibt
sich unter Nutzung von Gleichung 8:
W  E pot h   0
Gleichung 9: Lageenergie
E pot  E pot h   mgh
2. Beispiel: Beschleunigen eines Körpers aus dem Stand
Bedingungen, verwendete Gesetze
E  WBeschl .
F  s
F  konst.
Ekin  E0  WBeschl .
s


Ekin   F  cos  F , s ds
0
s
Ekin   F ( s)ds
0
Ekin  Fs
Ekin  Fs
Ekin  mas
a
Ekin  ma t 2
2
m
2
Ekin  at 
2
F  ma
a
s  t2
2
v  at
Gleichung 10: kinetische Energie
Ekin 
m 2
v
2
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 12
Physik Klasse 11.2: Mechanik 4
3. Beispiel: Spannen einer Feder
Die Vorgehensweise ist für das Spannen einer Feder analog: Man muss anhand
der Anfangsgegebenheiten entscheiden, ob die Richtungen von Weg und Kraft
übereinstimmen bzw. ob die wirkende Kraft konstant ist.
Abbildung 9
Beim Spannen muss man – wie jeder aus eigener Erfahrung weiß – die Kraft für
jede weitere Verlängerung der Feder steigern. Die Verlängerung der Feder und
die Kraft wirken in die gleiche Richtung.
F  D s
sE
W   F s  d s
Hookesches Gesetz
sA
s


W   F  cos  F , s ds
0
s
W   F ( s )ds
D
s
FE
Federkonstante
Verlängerung der Feder
Endkraft
0
Variante 1
Variante 2
s
s
W   F ( s )ds
W   F ( s )ds
0
0
s
s
W   D  sds
W   D  sds
0
0
s
 D  s2 
W 

 2 0
s
 D  s2 
W 

 2 0
D  s2
2
Dss
W 
2
W 
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 13
Physik Klasse 11.2: Mechanik 4
Gleichung 11: Spannarbeit
D  s2
W
2
W
FE  s
2
Gleichung 12: Spannenergie
W  E
W  E
ESpann 
D  s2
2
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
ESpann 
© H. Knopf
FE  s
2
S. 14
Physik Klasse 11.2: Mechanik 4
Übung 1
Eine Feder mit einer Federkonstanten von D  10 mN wird um 10 cm gedehnt.
Welche Höhe erreicht ein Körper der Masse 250g, wenn er durch diese Feder in
die Höhe geschleudert wird?
Lösung:
Ds 2
2
Ds 2
h
2mg
h  0, 02m  2cm
mgh 
Übung 2
Die Feder eines Kugelschreibers mit einer Federkonstanten von D  10 mN wird
um 10 cm gedehnt. Welche Höhe erreicht ein Kugelschreiber der Masse 20g,
wenn er durch diese Feder in die Höhe geschleudert wird?
Lösung:
Ds 2
2
Ds 2
h
2mg
h  0, 255m  25,5cm
mgh 
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 15
Physik Klasse 11.2: Mechanik 4
Übung 3
Ein Pkw rutscht bei einer Vollbremsung (ohne ABS) über eine ebene Strecke
von 50 m über trockenen Asphalt (µ=0,5).
a) Diskutieren Sie, ob die Masse des Fahrzeuges (Pkw, Lkw, ...) eine Rolle
bei diesem Vorgang spielt.
b) Welche Geschwindigkeit erreicht das Fahrzeug, wenn es zu Beginn eine
Geschwindigkeit von 120km  h1 hatte?
c) Wie lang ist der Bremsweg (unter sonst gleichen Bedingungen), damit das
Fahrzeug zum Stehen kommt?
Lösung
a) Diskussion
b) Berechnung
E kin WRe ib
E kinE  E kinA  FR s
m
2
m
2
m
2
1
2
v
2
E
 v A2   µFN s

v
2
E
 v A2   µFG s
v
2
E
 v A2   µmgs
v
2
E
 v A2   µgs



vE2  v A2  2 µgs
vE   2 µgs  v A2
vE   2  0,5  9,81 sm2  50m  120 ms : 3,6
2
vE   2  0,5  9,81 sm2  50m  33 13 ms 
2
vE  24,91206758 ms
vE  24,9 ms
vE  89,7 km
h
c) Bremsweg bis zum Stillstand
Variante 1
Variante 2

1 2
2
 v E  v A   µgs

2  0

v E  2µgs  v 2A
0  2µgs  v 2A
1
 v 2A  µgs
2
v2
s A
2µg
s  113, 26m
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
0  2µgs  v 2A
2µgs  v 2A
s
© H. Knopf
v 2A
 113, 26m
2µg
S. 16
Physik Klasse 11.2: Mechanik 4
Übung 4
Ein Fahrzeug der Masse 1050 kg bremst aus einer Geschwindigkeit von
90km  h 1 bis zum Stillstand ab. Welche Temperatur haben die Bremsscheiben
(20 kg Stahl), nach dem Bremsen, wenn sie vorher 20°C hatten?
(Hinweis: Der Wärmeaustausch mit der Umgebung kann vernachlässigt werden.)
Lösung:
Variante 1
Variante 2
E kin  Qauf
E kin  Qauf
m 2
v  ms cs  Te  Ta 
2
m 2
v  ms cs Te  ms cs Ta
2
m
ms cs Te  v 2  ms cs Ta
2
m 2
v  ms cs Ta
2
Te 
m s cs
m 2
v  ms cs T
2
m
T 
v2
2ms cs
T  34,9K
E  A  T
E  54,9C
1050kg
2
 25 ms   20kg  470 kgKJ 293,15K
2
Te 
J
470 kgK
293,15K
Te  328, 0569K
e  54,906915C
e  54,9C
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 17
Physik Klasse 11.2: Mechanik 4
4.1.4. Leistung
Wenn man sich lediglich die Energiemenge angibt, die bei einem Vorgang umgesetzt wird, so ist damit keine Aussage gemacht, wie lange dieser Vorgang
dauert. Insbesondere bei Maschinen ist es wichtig, zu wissen, wie viel Arbeit sie
in einer bestimmten Zeit verrichten können.
Als Maß für die pro Zeit umgesetzte Energiemenge bzw. die verrichtete Arbeit
pro Zeit wird die Leistung angegeben.
Gleichung 13: Durchschnittsleistung
P
E
W
bzw. P 
t
t
Bei Heizplatten meint man damit, wie viel Wärme pro Zeit die Platte abgeben
kann (thermische Leistung). Bei Maschinen ist die verrichtete mechanische
Arbeit pro Zeit gemeint (mechanische Leistung).
Analog gibt es eine elektrische Leistung, die die umgesetzte elektrische Energie pro Zeit angibt.
Handelt es sich um einen Vorgang, der mit gleichmäßiger Arbeitsverrichtung
verbunden ist, so ist die Gleichung 13 ausreichend.
Das Diagramm in Abbildung 10 zeigt das zeitliche Verhalten.
Abbildung 10: W-t-Diagramm
W
t
Es ist unschwer zu erkennen, dass die Gleichung 13 den Anstieg des Graphen
bestimmt.
Im Falle einer ungleichmäßigen Arbeitsverrichtung, muss man – wie bereits
vielfach getan – den Differenzenquotienten durch den Differentialquotienten
ersetzen, damit für bestimmten Moment die Augenblicksleistung bestimmen
kann.
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 18
Physik Klasse 11.2: Mechanik 4
Abbildung 11: W-t-Diagramm für eine ungleichmäßige Arbeitsverrichtung
Für einen bestimmten Augenblick beträgt die Leistung dann:
Gleichung 14: Augenblicksleistung
P
dW
dt
…
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 19
Physik Klasse 11.2: Mechanik 4
4.2. Register Kurshalbjahr 11.2 : Mechanik 4 – Arbeit, Energie, Leistung
Arbeit 1, 4, 6, 7, 9, 10, 11, 18, 20,
21, 22
Augenblicksleistung 18, 19
Chemie 5
Endkraft 13
Energie 1, 4, 5, 10, 12, 18, 20, 21,
22
Energie, thermische 4
Erhaltung der Energie 5
Feder 5, 7, 13
Federkonstante 13
freier Fall 10
Geschwindigkeit 16, 17
Gewichtskraft 11
Heben 10, 11, 12
Hookesches Gesetz 7, 13
Hubarbeit 11, 12
Kernenergie 5
Kraft 6, 7, 8, 9, 13
Lageenergie 4, 5, 11, 12
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
Leistung 1, 4, 18, 19
Leistung, mechanische 18
Leistung, thermische 18
Licht 4, 5
Masse 16, 17
Mechanik 4, 5, 20, 21, 22
Momentleistung Siehe
Augenblicksleistung
Physik 23
Quantenphysik 5
Skalarprodukt 6
Spannarbeit 14
Spannenergie 5, 14
Temperatur 4, 17
Thermodynamik 5, 22
Vollbremsung 16
Wärme 4, 5, 18, 22
Wärmeaustausch 17
Weg 6, 7, 9, 13
Zustandsgröße 4
© H. Knopf
S. 20
Physik Klasse 11.2: Mechanik 4
4.3. Verzeichnis der Abbildungen, Tabellen, Quelltexte und Definitionen
Kurshalbjahr 11.2 : Mechanik 4 – Arbeit, Energie, Leistung
Abbildungen:
Abbildung 1 ........................................................................................................... 4
Abbildung 2: Schleppen eines Tankers (1) ........................................................... 6
Abbildung 3: Schleppen eines Tankers (2) ........................................................... 6
Abbildung 4 ........................................................................................................... 7
Abbildung 5: F-s-Diagramm für das Spannen einer Feder ................................... 7
Abbildung 6 ........................................................................................................... 8
Abbildung 7: Arbeit – Energie ............................................................................ 10
Abbildung 8 ......................................................................................................... 11
Abbildung 9 ......................................................................................................... 13
Abbildung 10: W-t-Diagramm ............................................................................ 18
Abbildung 11: W-t-Diagramm für eine ungleichmäßige Arbeitsverrichtung .... 19
Definitionen:
Definition 1: Energie ............................................................................................. 4
Definition 2 Energie 2 ........................................................................................... 4
Definition 3: mechanische Arbeit ......................................................................... 6
Gleichungen, Formeln
Gleichung 1 ........................................................................................................... 6
Gleichung 2: Skalarprodukt zur Berechnung der Arbeit ...................................... 6
Gleichung 3: Skalarprodukt zur Berechnung der Arbeit ...................................... 6
Gleichung 4: Federspannarbeit.............................................................................. 8
Gleichung 5 ........................................................................................................... 8
Gleichung 6: mechanische Arbeit ......................................................................... 9
Gleichung 7 ......................................................................................................... 11
Gleichung 8: Hubarbeit ....................................................................................... 12
Gleichung 9: Lageenergie ................................................................................... 12
Gleichung 10: kinetische Energie ....................................................................... 12
Gleichung 11: Spannarbeit .................................................................................. 14
Gleichung 12: Spannenergie ............................................................................... 14
Gleichung 13: Durchschnittsleistung .................................................................. 18
Gleichung 14: Augenblicksleistung .................................................................... 19
Tabellen:
Tabelle 1: Beispiele für Energieformen ................................................................ 5
Tabelle 2: Quellen ............................................................................................... 22
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 21
Physik Klasse 11.2: Mechanik 4
4.4. Quellen Kurshalbjahr 11.2 : Mechanik 4 – Arbeit, Energie, Leistung
Tabelle 2: Quellen
1
2
Formeln und Tabellen für die Sekundarstufe I und II
Paetec 1996
Chr. Gerthsen, H.
Vogel (Hersg.)
Gerthsen Physik
Springer Verlag 1999
3
E. Grimsehl, W.
Schallreuter, K. Altenburg (Hersg.)
Grimsehl
Lehrbuch der Physik
Band 1: Mechanik, Akustik, Wärmelehre
B.G. Teubner Verlagsgesellschaft 1985 (1991)
4
W. Bredthauer, W.
Groß-Berhag
Czech, R. v. Dwinge- Schwingungen und Wellen
lo-Lütten, u.a.
Klett Verlag 1996
5
R. Sexl, I. Raab
(Hersg. K.Jupe, M.
Ludwig)
Kursthemen Physik
Mechanik, Thermodynamik
Diesterweg Verlag 1995
6
B. Ebert, Chr. Hache,
W. Krug, K. Liebers,
R. Reichwald, W.
Scholz, H.-J. Wilke,
R. Winter
Lehrbuch Physik Sekundarstufe II
Gesamtband
Mechanik, Elektrizitätslehre, Thermodynamik, Optik, Kernphysik, Relativitätstheorie
Volk und Wissen Verlag 1995
7
H. Knopf
Mechanik in der Sekundarstufe II
Manuskript (1994-2003)
8
J. Grehn, J. Krause
Metzler Physik
Schroedel Verlag 1998
9
G. Boysen, H. Heise, Oberstufe Physik
J. Lichtenberger u.a. Ausgabe E
Cornelsen Verlag 2001
10
F. Dorn, F. Bader
Physik
Oberstufe
Band MS
Schroedel Verlag 1995
11
O. Höfling
Physik
Band II, Teil 1: Mechanik – Wärme
Dümmler Verlag 1992
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 22
Physik Klasse 11.2: Mechanik 4
12
H. Lindner
Physikalische Aufgaben
Fachbuchverlag Leipzig / Carl Hauser Verlag
(24. Auflage 1984, ... , 32. Auflage 2001)
13
O. Höfling
Physikaufgaben Sekundarstufe II
Dümmler Verlag 1992 (und spätere Ausgaben)
14
F. Dittmer, E. Kaminski, H.-P. Pommeranz, G. Riedl, R.
Schülbe, Chr. Weber
Rahmenrichtlinien Physik
Land Sachsen-Anhalt 2003
15
I. N. Bronstein, K.A.
Semendjajew
Taschenbuch der Mathematik
Teubner Verlagsgesellschaft 1985
16
L. Meyer, G.-H.
Schmidt
Physik
Gymnasiale Oberstufe
Paetec Verlag 2004
Physik_Klasse11_2-04-Mechanik-Dynamik-Arbeit-EnergieLeistung_ON1516.docx * April 2016 V2.5.7
© H. Knopf
S. 23