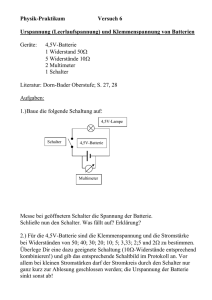
Inhaltsverzeichnis

Inhaltsverzeichnis
1
2
Versuchsbeschreibung und Physikalische Grundlagen
Werteaufnahme und Auswertung
2.1
2.2
3
1
2
Bestimmung der Klemmenspannung einer Gleichspannungsquelle
. . . . . . . . . . . .
2
2.1.1
Untersuchung der Temperaturabhängigkeit der Gegenspannung
. . . . . . . . .
2
2.1.2
Messwertaufnahme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2.1.3
Auswertung und Ermittlung der Klemmenspannung
3
. . . . . . . . . . . . . . .
Bestimmung von Urspannung und Innenwiderstand eines Trockenelementes
. . . . . .
Diskussion
4
6
3.1
Fehlerdiskussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
3.2
Ergebnisdiskussion
6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
Literatur
6
A
Herstellerangaben des Weston-Normalelementes
7
B
Datenprotokollierung während des Versuches
8
1 Versuchsbeschreibung und Physikalische Grundlagen
Im zu bearbeitenden Experiment wurde die Methode der Kompensation verwendet, um die Klemmenspannung
U2
einer Gleichspannungsquelle sowie Innenwiderstand
Ri
und Urspannung
U0
eines
Trockenelementes zu bestimmen. Dazu wurde am Versuchsplatz eine Schaltung der Form links in Abbildung 1 aufgebaut.
Abbildung 1: Schaltung des Versuchs, links mit Normalement, rechts mit Trockenelement
Mit dem Normalelement
U1
und dem Widerstand des Schleifkontaktes sollte der Stromuss im oberen
Stromkreis verschwinden, wobei diese Situation durch Verschieben des Kontaktes und Kontrolle mit
dem Galvanometer G herbeigeführt wird. Das Galvanometer arbeitet zum Anzeigen des Vorhandenseins von Strom zuverlässiger als ein herkömmliches Amperemeter. Für die Spannung
Widerstand
Rx
gilt dann nach [1], S.28
Bei nichtvorhandenem Strom ist
Ux = U1
x
Ux = U2 .
L
über dem
(1)
und damit
L
U2 = U1 .
x
Mit der nun bekannten Spannung
Ux
(2)
U2 der Gleichspannungsquelle kann die rechte Schaltung in Abbildung
1 aufgebaut werden. Bei dem Trockenelement handelt es sich um eine handelsübliche Batterie. Aus der
Maschenregel folgt
U0 = IRi + UK
UK = −IRi + U0 .
Mit der Potentiometerschaltung können nun beliebige Ströme
(3)
I
eingestellt werden. Die anliegende
Klemmenspannung lässt sich wie im ersten Teil des Experimentes mithilfe der Schleifkontaktschaltung
und der Gleichung (1) ermitteln. Eine lineare Regression über (3) kann dann schlieÿlich die gesuchten
Gröÿen liefern.
Eine detaillierte Versuchsbeschreibung ndet sich in [1], S.26-29.
1
2 Werteaufnahme und Auswertung
2.1 Bestimmung der Klemmenspannung einer Gleichspannungsquelle
2.1.1 Untersuchung der Temperaturabhängigkeit der Gegenspannung
Für den ersten Teil konnte mit einem Weston-Normalelement der Spannung
U1
gearbeitet werden,
welches auf chemischer Basis operiert und temperaturabhängig ist. Die Herstellerangaben zur Temperaturabhängigkeit nden sich in Anhang A. Trägt man die Herstellerangaben in einem
U -ϑ-Diagramm
auf, lässt sich über diese Daten eine lineare Regression ausführen, um eine Umrechnungsformel für die
Spannung U des Normalelements in V
Temperaturabhängigkeit von
U1
zu erhalten. Dargestellt ist die Regression in Abbildung 2.
Korrigierte Werte des Herstellers
Regression der Form
U(ϑ) = A · ϑ + Uϑ0, mit
A = ( -46 ± 1 ) μV/°C
Uϑ0 = ( 101956 ± 3 ) μV
1,0188
1,0187
1,0186
U1 = ( 1.01865 ± 0.00004 ) V
1,0185
1,0184
1,0183
1,0182
ϑ1 = ( 19.9 ± 0.2 ) °C
1,0181
16
18
20
22
24
Temperatur ϑ in °C
26
28
30
Abbildung 2: Temperaturabhängigkeit des Normalelementes
Die Umrechnungsformel hat damit die Form
Uϑ = A · ϑ + Uϑ0 ,
(4)
mit den Gröÿen
A = (−46 ± 1)
µV
◦C
Uϑ0 = (101956 ± 3) V.
2.1.2 Messwertaufnahme
Nun wurde zehnmal die Position des Schleifkontaktes gesucht, bei dem das Galvanometer keinen Stromuss mehr anzeigte. Dabei ist zu beachten, dass aus Gründen der Übersichtlichkeit am Versuchsplatz
die Millimeterskala des Schleifkontaktes verkehrt herum positioniert wurde, sodass in Wirklichkeit die
Gröÿe
x2 = L − x
gemessen wurde. Die Länge des Kontaktes betrug
(5)
L = (100.0±0.1) cm. In Tabelle 1 sind die Messwerte
dargestellt.
2
Messung
i
Schleifkontaktposition
x2,i
Temperatur des
[cm]
Weston-Elements
1
57.3
20.1
2
57.2
19.9
3
57.2
19.9
4
57.2
19.8
5
57.4
19.8
6
57.3
19.8
7
57.3
19.8
8
57.4
19.8
9
57.4
19.8
10
57.3
19.8
ϑi
◦
[ C]
Tabelle 1: Ermittlung der nötigen Schleifkontaktposition
2.1.3 Auswertung und Ermittlung der Klemmenspannung
◦
Nach [2], S.18 beträgt die Unsicherheit des Thermometers, welches eine Zehntel- C-Einteilung besaÿ,
uϑ = 0.2◦ C. Wie man sieht, war die während der Messung herrschende Temperatur im Normalelement
also innerhalb ihrer Unsicherheit konstant, sodass eine Mittelwertbildung über die Temperatur möglich
ist.
Der Spielraum des Schleifkontaktes selbst lieÿ für die Position keine geringere systematische Abweichung als
ux2 = 0.2 cm
zu.
Damit kann nun eine Mittelwertbildung der gemessenen Gröÿen vorgenommen werden. Die Auswertung erfolgt in Tabelle 2.
Instrumentelle Gröÿe
Mittelwert
Standardabweichung
Vertrauensbereich
Systematische Abweichung
Unsicherheit
Endwert
Position [cm]
57.3
0.08
0.03
0.2
0.2
x2 = (57.3 ± 0.2) cm
◦
Temperatur [ C]
19.85
0.1
0.03
0.2
0.2
ϑ = (19.9 ± 0.2)
◦C
Tabelle 2: Ermittlung der endgültigen Schleifkontaktposition und Normalelementtemperatur
Bei dieser Temperatur beträgt die Spannung
U1
des Normalelementes nach (4)
U1 = 1.01865 V.
Die Unsicherheit ergibt sich nach dem Gauÿ'schen Fehlerfortpanzungsgesetz zu
uU1
s
∂U1 2
∂U1 2
∂U1 2
uA
+ uUϑ0
+ uϑ
=
∂A
∂Uϑ0
∂ϑ
q
= (uA · ϑ)2 + u2Uϑ0 + (uϑ · A)2
p
= 22 + 32 + 12 · 10−5 V
= 4 · 10−5 V.
3
(6)
Dies entspricht der graschen Darstellung der Fehlerfortpanzung in Abbildung 2.
Mit (5) modiziert sich (4) zu
U2 = U1
L
.
L − x2
Für dessen Unsicherheit gilt dann
uU2
s
∂U2 2
∂U2 2
∂U2 2
=
+ uL
+ ux2
uU1
∂U1
∂L
∂x2
s
2 2 2
L
L
x2
=
uU1
+ uL U1
+ ux2 U1
L − x2
(L − x2 )2 1
(L − x2 )2
p
= 12 + 322 + 1132 · 10−4 V
= 0.01 V.
Damit lautet das Endergebnis schlieÿlich
U2 = (2.39 ± 0.01) V.
2.2 Bestimmung von Urspannung und Innenwiderstand eines Trockenelementes
Nun wurden Schleifkontaktpositionen für Ströme im Bereich von
0.14 mA < I < 0.7 mA ermittelt. Diese
Ströme haben eine Unsicherheit von 2.5% des Messbereichs (MB) des Amperemeters, welcher während
der Messung unverändert auf
1 mA
gestellt war, womit die Unsicherheit stets
Die Unsicherheit der Kontaktposition beträgt wiederum stets
ux2 = 0.2 cm.
uI = 0.03 mA
beträgt.
Mit dieser Position lässt
sich ähnlich des ersten Teils des Versuches die Klemmenspannung des oberen Schaltkreises bestimmen.
Mit (5) folgt aus (1)
x2 UK = U2 1 −
.
L
Die Unsicherheit ergibt sich dann aus dem Gauÿ'schen Fehlerfortpanzungsgesetz zu
s
∂UK 2
∂UK 2
∂UK 2
uU2
uUK =
+ ux2
+ uL
∂U2
∂x2
∂L
s
x2 2
x 2 2
U2 2 =
uU2 · 1 −
+ ux2 ·
+ uL · U2 · 2
L
L
L
p
= 722 + 482 + 92 · 10−4 V
= 0.009 V.
Die exemplarische Rechnung für das erste Wertepaar zeigt, dass aus der Gleichspannungsquelle der
dominierende Fehler resultiert. In Tabelle 3 folgt die Errechnung der Klemmenspannungen.
Über diese Werte lässt sich nun eine lineare Regression der Form von (3) durchführen. Dabei ist
es sinnvoll, nach den Ordinatenwerten zu gewichten. Eine mit dem Program QtiPlot durchgeführte
Regression liefert Abbildung 3 und die Endwerte
Ri = (1046 ± 8) Ω,
U0 = (1.621 ± 0.004) V.
4
Stromstärke
I
Stellung des
Klemmenspannung am
Schleifkontaktes
Trockenelement
x2
[mA]
UK
[cm]
Unsicherheit
uUK
[V]
[V]
0.14
38.5
1.467
0.009
0.20
40.9
1.410
0.009
0.24
42.6
1.369
0.009
0.30
45.0
1.312
0.008
0.34
46.7
1.272
0.008
0.40
49.8
1.198
0.008
0.44
51.2
1.164
0.008
0.50
53.7
1.105
0.008
0.54
55.8
1.054
0.007
0.60
58.5
0.990
0.007
0.64
60.0
0.954
0.007
0.70
62.9
0.885
0.007
Tabelle 3: Beziehung zwischen Strom und Klemmenspannung
0,1
0,2
0,3
0,4
0,5
0,6
0,7
Spannung Uk am Trockenelement in V
1,6
1,6
Ermittelte Werte
Regression der Form
Uk(I) = - R · I + U0, mit
R = ( 1046 ± 8 ) Ω
U0 = ( 1.621 ± 0.004 ) V
1,5
1,4
1,5
1,4
1,3
1,3
1,2
1,2
1,1
1,1
1
1
0,9
0,9
0,8
0,8
0,1
0,2
0,3
0,4
0,5
Stromstärke I in mA
0,6
0,7
Abbildung 3: Regression zur Ermittlung der Eigenschaften des Trockenelementes
5
3 Diskussion
3.1 Fehlerdiskussion
Wie man zum Schluss der Auswertung sehen kann, ist der dominierende Fehler des Experimentes die
Gleichspannungsquelle. Um diese genauer ermitteln zu können, muss der dominierende Fehler im ersten
Teil des Versuchs identiziert werden.
In (6) sieht man, dass die Regressionsgröÿen aus der Temperaturkorrektur den gröÿeren Einuss auf die
Unsicherheit des Normalelementes haben. Auch in Abbildung 2 sieht man, dass die Werteangaben des
Herstellers nicht unbedingt linear verlaufen. Eine angepasste Regression brächte hier möglicherweise
geringere Fehler in den Regressionsgröÿen und damit ein sicheres
U2 .
Doch auch die Unsicherheit der
Temperatur ist noch in der gleichen Gröÿenordnung. Die Verwendung eines digitalen Präzisionsthermometers könnte hier genauere Ergebnisse liefern.
Allerdings zeigt sich dann in der Ermittlung von
U2 ,
dass vor allem die Längenmessungen die Unsi-
cherheit vergröÿern. Die groÿe systematische Abweichung der Kontaktposition durch den Spielraum
des angebrachten Zeigers hat den beträchtlichsten Einuss. Ein Vorteil dieser Unsicherheit ist, dass
dadurch der 1.5%-ige Fehler des Galvanometers nicht berücksichtigt werden musste. Würde sie verringert, müsste das Galvanometer mit in die Betrachtung eingehen. Trotzdem wäre diese Betrachtung der
groÿen Unsicherheit des Kontaktes vorzuziehen. Um diesen Fehler zu verringern, könnte das Spiel des
Kontaktes geschmeidiger gestaltet werden, z.B. durch eine geölte Schiene. Auch ein direkt auf der Messskala liegender Anzeiger des Kontaktes lieÿe die systematische Unsicherheit schrumpfen. Letztendlich
könnte eine noch feinere Skala auf dem Schleifkontakt installiert werden.
3.2 Ergebnisdiskussion
Die Resultate liegen im gleichen Bereich wie die anderer Versuchsgruppen. Auch die Urspannung der
Batterie ist in der erwarteten Gröÿenordnung (1.5V), wenn auch etwas gröÿer. Allerdings übertrit der
Innenwiderstand die eigentliche Erwartung. Innenwiderstände im Kiloohm-Bereich sind für Batterien
keineswegs die Regel, sondern für den normalen Gebrauch eigentlich ungeeignet, da zu geringe Ströme
aus der Spannungsquelle geliefert werden.
Das legt die Vermutung nahe, dass die verwendete Batterie ein für den Lehrbetrieb modiziertes Modul
darstellt, welches extra einen groÿen Innenwiderstand besitzt. Eine entsprechende Schaltung mit einem
zusätzlichen Widerstand würde diese Ergebnisse erklären.
4 Literatur
[1] Skript: Physikalisches Grundpraktikum - Elektrodynamik und Optik von Dr. Uwe Müller, Berlin
2005
[2] Skript: Physikalisches Grundpraktikum - Einführung in die Messung, Auswertung und Darstellung
experimenteller Ergebnisse in der Physik von Dr. Uwe Müller, Berlin 2007
6
A Herstellerangaben des Weston-Normalelementes
Abbildung 4: Herstellerangaben auf dem Normalelement
7
B Datenprotokollierung während des Versuches
8