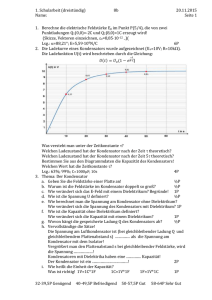
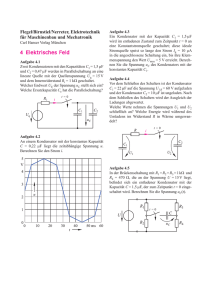
RC-Transiente, Umladung pdf

Grundlagen der Elektrotechnik
Übungsaufgaben
30)
Kondensator, Temperaturabhängigkeit.
Durch die Parallelschaltung zweier Kondensatoren soll eine Kapazität von
270 pF mit einem TK-Wert von null gebildet werden. Verfügbar sind Kondensatoren mit TK-Werten von +80 · 10−6 K −1 und von −400 · 10−6 K −1 .
a)
31)
C1
C2
TK1 TK2
Berechnen Sie die erforderlichen Werte der Einzelkondensatoren.
(Lsg.: C1 = 225 pF, C2 = 45 pF)
Umladung von Kondensatoren.
A
Der Kondensator C1 ist auf die Spannung U1 aufgeladen. Die Kondensatoren C2 und C3 sind sind nicht geladen.
C2 U2
U1 = 150 V, C1 = 8 nF, C2 = 3 nF, C3 = 6 nF
U1 C1
C3 U
3
B
a)
b)
c)
d)
e)
f)
32)
Berechnen Sie die im Kondensator C1 gespeicherte Ladung. (Lsg.: Q1 = 1.2 · 10−6 As)
Berechnen Sie die Kapazität der Reihenschaltung von C2 und C3 . (Lsg.: C23 = 2 nF)
Der Schalter wird geschlossen. Berechnen Sie die Kapazität zwischen den Klemmen A
und B. (Lsg.: Cges = 10 nF)
Berechnen Sie die jetzt am Kondensator C1 anliegende Spannung. (Lsg.: U1 = 120 V)
Berechnen Sie die Ladung der Kondensatoren C2 und C3 . (Lsg.: Q = 240 · 10−9 As)
Berechnen Sie die an den Kondensatoren C2 und C3 anliegenden Spannungen.
(Lsg.: U2 = 80 V, U3 = 40 V)
Kondensator, Entladung.
Ein Kondensator mit der Kapazität C = 1 pF ist auf die Spannung
U0 = 100 V aufgeladen. Zum Zeitpunkt t = 0 wird der Schalter geschlossen und der Kondensator entlädt sich über den Widerstand R = 1 kΩ.
a)
b)
c)
33)
R
u(t)
C
Berechnen Sie die Kondensatorspannung u(t) als Funktion der Zeit.
Berechnen Sie den im Kreis ieÿenden Strom i(t) als Funktion der Zeit.
Skizzieren Sie den zeitl. Verlauf von Kondensatorspannung u(t) und -strom i(t).
RC-Schaltung, Aufladung.
Das RC-Glied ist mit dem Widerstand RL belastet. Zum Zeitpunkt
t = 0 wird das RC-Glied samt Lastwiderstand RL an die Spannung
U1 gelegt.
U1 = 100 V, R = 1 M Ω, RL = 470 kΩ, C = 1 µF
a)
b)
c)
Geben Sie die Kondensatorspannung uC (t) als Funktion der Zeit an.
Berechnen Sie den Endwert der Ladespannung uC .
(Lsg.: uC (t = ∞) = 31.97 V)
Nach welcher Zeit ist der Kondensator zu mehr als 99% aufgeladen?
(Lsg.: t = 1.47 s ≈ 5 · τ = 1.6 s)
9
i
R
U1
u(t)
iC
iL
C R
L
34)
Kondensator-Aufladung, Strom- und Spannungsquelle.
In der Schaltung mit je einer Strom- und Spannungsquelle wird zur Zeit t = 0 der Schalter
geschlossen.
U0 = 12 V
I0 = 100 mA
R1 = 340 Ω
R2 = 100 Ω
R4 = 1.44 kΩ R5 = 288 Ω
a)
b)
c)
d)
F. Kappen, (et1_aufg_part-), Stand: Mon. 23-Jan-2017 20:29:37
e)
35)
C = 100 nF
R3 = 100 Ω
R3
R1
U0
t=0
R2
C
I0
R4
R5
Berechnen Sie die Spannung uC (t = −0) am Kondensator. (Lsg.: 9.83 V)
Berechnen Sie für t → ∞ den Endwert der Kondensatorspannung. (Lsg.: 18 V)
Berechnen Sie die Zeitkonstante der Umladung. (Lsg.: 27 µs)
Berechnen Sie die Zeit, zu der der Kondensator weniger als 100 ppm vom Endwert
abweicht. (Lsg.: 227.35 µs)
Berechnen Sie den maximalen Strom durch R2 . (Lsg.: 30.26 mA)
Kondensator, Energie.
Die Kondensatoren C1 und C2 sind bei geönetem Schalter auf die Spannungen U1 bzw. U2 aufgeladen.
U1 = 120 V, U2 = 60 V, C1 = 10 µF, C2 = 5 µF
a)
b)
c)
d)
e)
U1 C1 R C2 U2
Berechnen Sie die Gesamtkapazität. (Lsg.: Cges = 3.33 µF)
Berechnen Sie die in den Kondensatoren gespeicherte Energie. (Lsg.: Wa = 81 mWs)
Der Schalter wird geschlossen. Berechnen Sie die Spannung an den Kondensatoren.
(Lsg.: U = 100 V)
Berechnen Sie die jetzt in den Kondensatoren gespeicherte Energie. (Lsg.: Wb = 75 mWs)
Diskutieren Sie das Ergebnis aus d).
10