Serie3

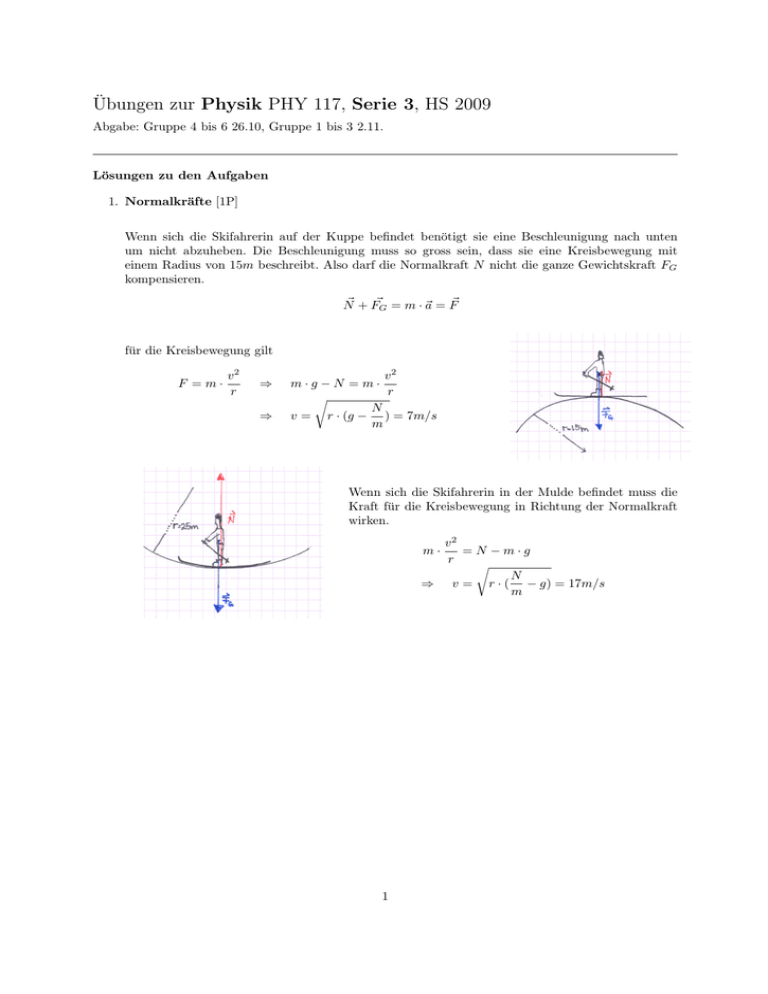
Übungen zur Physik PHY 117, Serie 3, HS 2009
Abgabe: Gruppe 4 bis 6 26.10, Gruppe 1 bis 3 2.11.
Lösungen zu den Aufgaben
1. Normalkräfte [1P]
Wenn sich die Skifahrerin auf der Kuppe befindet benötigt sie eine Beschleunigung nach unten
um nicht abzuheben. Die Beschleunigung muss so gross sein, dass sie eine Kreisbewegung mit
einem Radius von 15m beschreibt. Also darf die Normalkraft N nicht die ganze Gewichtskraft FG
kompensieren.
~ + F~G = m · ~a = F~
N
für die Kreisbewegung gilt
F =m·
v2
r
⇒
⇒
v2
m·g−N =m·
r
r
N
v = r · (g − ) = 7m/s
m
Wenn sich die Skifahrerin in der Mulde befindet muss die
Kraft für die Kreisbewegung in Richtung der Normalkraft
wirken.
v2
=N −m·g
r
r
N
⇒ v = r · ( − g) = 17m/s
m
m·
1
2. Beschleunigung und Kräfte [3P]
Auf den Affen wirken die Gewichtskraft F~G und die Seilkraft F~S , die den Affen hochzieht. Für die totale Kraft die
auf den Affen wirkt gilt:
F = mA · aA = FS − FG = FS − mA · g
⇒
FS = mA · aA + mA · g
Die Seilkraft ist auf der Seite der Kiste gleich gross wie auf
der Seite des Affen. Somit gilt für die Kiste:
F = mK · aK = FS − FK = mK · g − FS
Die Kiste hebt in dem Moment ab wo die Seilkraft gleich
gross ist wie die Schwerkraft. Also muss gelten:
FS = mK · g
Setzt man nun FS = mA · aA + mA · g ein erhält man:
aA = g ·
mK − mA
= 5m/s2
mA
Hält sich der Affe am Seil fest und ist die Kiste in der Luft, so ist die Kraft auf das gesamte System
die Differenz zwischen den beiden Gewichtskäften die auf die gesamte Masse des Systems wirken.
F = mtotal · atotal = (mK + mA ) · atotal = mK · g − mA · g
mK − mA
· g = 2m/s2
⇒ atotal =
mK + mA
3. Schiefe Ebene [2P]
(b) Die Kräfte die auf die Masse m1 in x1 -Richtung wirken sind Fm1 = m1 · g · sin(α) und
Fm2 = m2 · g. Mit sin(30◦ ) = 0.5 gilt:
1
· m1 · g < m2 · g
2
Also bewegen sich die Massen in −x1 -Richtung bzw in x2 -Richtung.
(c) Die Beschleunigung erhält man aus der totalen Kraft die auf die gesamte Masse wirkt. Die
totale Kraft ist die Differenz Fm1 − Fm2 .
³
m1 ´
F = mtotal · atotal = (m1 + m2 ) · atotal = m2 · g − m1 · g · sin(α) = g · m2 −
2
(m2 − m21 )
⇒ atotal = g ·
= 1m/s2
m1 + m2
2
(d) Um die Fadenkraft FS zu bestimmen, betrachten wir die Masse m1 . Die Kräfte die auf m1 in
x1 -Richtung wirken sind die Fadenkraft FS und die Gewichtskraft Fm1 = m1 · g · sin(α). Es gilt
Fbeschl. = m · ẍ = m · (−abeschl. ) = FS − Fm1
⇒ Fs = Fm1 + Fbeschl.
m1 · g
FS =
+ m1 · abeschl. = 18N
2
⇒
(e)
Fm1
Um ein Gleichgewicht zu erhalten müssen die Kräfte auf eine Masse gleich Null sein.
µ
¶
m2
m2
− Fm2 = 0 ⇒ m1 · g · sin(α) = m2 · g ⇒
= sin(α) ⇒ arcsin
= 41.8◦
m1
m1
4. Bewegungsgleichung eines fallenden Seils [3P]
(a) Nur der Anteil des Seils der bereits über die Tischkannte gegleitet ist übt eine Kraft auf das
gesamte Seil aus die zur Beschleunigung beiträgt. Also ist FG = m · xl · g. Diese Kraft wirkt auf das
ganze Seil mit F = m · a = m · ẍ. Die Bewegungsgleichung ist dann:
m · ẍ = m ·
g
·x
l
⇒
ẍ =
g
·x
l
⇒
ẍ −
g
·x=0
l
(b) Aus der Bewegungsgleichung sieht man, dass die gesuchte Lösung für x nach zweimaligem
Ableiten wieder sich selbst multipliziert mit einer Konstante ergeben muss. Die Exponentialfunktion
p
eα·t erfüllt diese Bedingung. Setzt man diese funktion in ẍ − gl · x = 0 ein, erhält man α = ± gl .
Nun muss die Löesung allerdings ein Linearkombination der beiden α’s sein. Also wählen wir einen
allgemeinen Ansatz der die Bewegungsgleichung erfüllen kann.
x(t) = A · eα·t + B · e−α·t
Um nun noch die Konstanten A und B zu bestimmen brauchen wir zwei Anfangsbedingungen. Wir
wissen dass x(t = 0) = x0 ist und, dass das Seil im Moment t = 0 losgelassen wird, das heisst
v(t = o) = v0 = 0.
Mit der Anfangsbedingung für x0 erhalten wir mit t = 0:
x0 = A + B
Für die zweite Anfangsbedingung v0 = 0 müssen wir zuerst x(t) einmal nach der Zeit ableiten:
v0 = α · A · eα·0 − α · B · e−α·0 = α · A − α · B
3
Aus diesen zwei Gleichungen erhält man A = B und A = x20 . Somit ergibt sich für den Ansatz x(t):
√g
√g
(e l ·t + e− l ·t )
x(t) = x0 ·
2
Verwendet man die Formel für cosh(γ · t) =
eγ·t +e−γ·t
2
so ist
r
g
x(t) = x0 · cosh(
· t)
l
5. Queen Mary 2 [3P]
(a)
Die Bewegungsgleichung lautet:
m · a = FA − FR
= FA − β · v
⇒m·
(b)
dv
= FA − β · v
dt
Ist die Endgeschwindigkeit erreicht, so ist die Beschleunigung, a = 0.
m · a = FA − β · v = 0
⇒
v=
FA
β
Bei konstanter Antriebskraft ergibt sich für die Leistung:
P = FA · v = β · v 2
P
117M W
⇒β= 2 =
= 5.0 · 105 kg/s
v
(55km/h)2
FA = β · v = 7.7 · 106 N
(c) Zur Bestimmung der Zeitkonstante benutzen wir die Bewegungsgleichung m · v̇ = FA − β · v.
Dann gilt:
v̇ +
β
FA
·v =
= konstant
m
m
Diese Gleichung zeigt dass die Lösung für v(t) auch einen zeitunabhängigen Teil hat. Wir interessieren uns aber nur für den zeitabhängigen Teil der Funktion und darum betrachten wir die
Gleichung:
v̇ +
Mit dem Ansatz f (x) = e−λ·t findet man λ =
β
·v =0
m
β
m
β
= 3.3 · 10−3 s−1
m
1
τ = = 300s
λ
λ=
(d)
Hamburg
19. Oktober 2009
4