einführung (1.9b) - Fakult at f ur Physik
Werbung
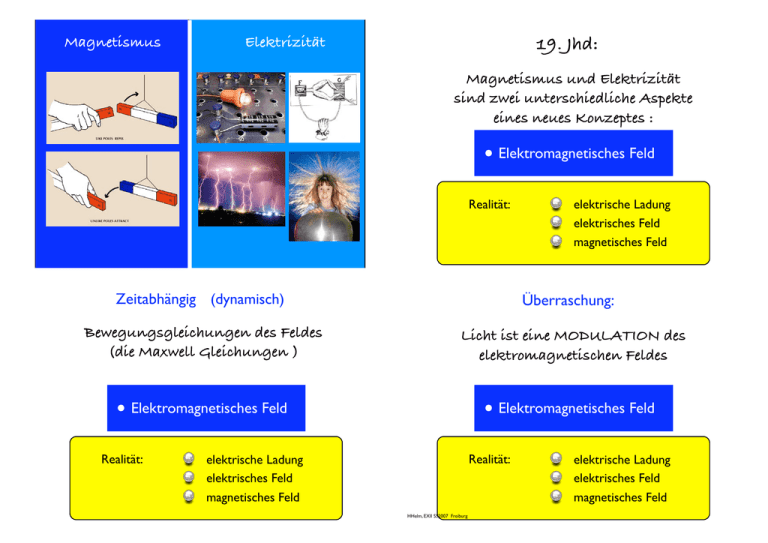
Magnetismus 19. Jhd: Elektrizität Magnetismus und Elektrizität sind zwei unterschiedliche Aspekte eines neues Konzeptes : • Elektromagnetisches Feld Realität: Zeitabhängig (dynamisch) elektrische Ladung elektrisches Feld magnetisches Feld Überraschung: Bewegungsgleichungen des Feldes (die Maxwell Gleichungen ) Licht ist eine MODULATION des elektromagnetischen Feldes • Elektromagnetisches Feld • Elektromagnetisches Feld Realität: Realität: elektrische Ladung elektrisches Feld magnetisches Feld HHelm, EXII SS2007 Freiburg elektrische Ladung elektrisches Feld magnetisches Feld elektrische Ladungen AMPLITUDE MODULATION ZEIT elektrische Ladungen positive und negative Ladungen unterscheiden sich in der Richtung der Ablenkung im Magnetfeld es gibt positive und negative Ladungen ! F! = q !v × B e : Elementarladung q immer in Einheiten von e = 1.6 × 10−19 C HHelm, EXII SS2007 Freiburg Ladung ist an Masse-behaftete Teilchen gebunden qp = +e qp̄ = −e qe = −e qē = +e fundamentale Ladungsmenge freier Teilchen Quarks Proton = uud Neutron = udd Ladung ist an Masse-behaftete Teilchen gebunden qe = −qp genau auf 10−20 Gesamt-Ladung bleibt in einem abgeschlossenem System konstant Man kann Ladungsträger nicht einzeln erzeugen entweder Ladungsträger trennen oder paarweise (+ und -) erzeugen e = 1.602177... × 10−19 C HHelm, EXII SS2007 Freiburg Gesamt-Ladung bleibt in einem abgeschlossenem System konstant in Gewitterwolken ReibungsElektrizität H+ + OHIonenbildung Gesamt-Ladung bleibt in einem abgeschlossenem System konstant Paarbildung eines Elektrons und Positrons Ladungstrennung Zerfall eines Neutrons Ladungstrennung A + hν → A+ + e− A + A → A + A+ + e− Photo-Ionisation Stoss-Ionisation Reibungs-Elektrizität HHelm, EXII SS2007 Freiburg Vergleich der Kräfte Stärke |F | für 2 Protonen Atom kollabiert nicht ! Gravitation Coulomb-Kraft 2 |F!G | = fG m1r·m 2 2 |F!C | = fc Q1r·Q 2 1 Proton 34 5 × 10 Elektron QM Vorzeichen immer anziehend je nach Vorzeichen des Produktes Q1 · Q2 Reichweite 1 r2 1 r2 ∆p · ∆x ≥ h̄ unmöglich makroskopisch fast immer Heisenberg Unschärferelation Neutralisation Stabilität von Materie Kombination von elektrischen Kräften und Quanteneffekten makroskopische elektrische Eigenschaften Leiter - Nichtleiter Elektronen Affinität Quantenmechanik und statistische Physik HHelm, EXII SS2007 Freiburg Vergleich der Kräfte Coulomb-Kraft Gravitation Coulomb-Kraft 2 |F!G | = fG m1r·m 2 2 |F!C | = fc Q1r·Q 2 1 5 × 1034 Vorzeichen immer anziehend je nach Vorzeichen des Produktes Q1 · Q2 Reichweite 1 r2 1 r2 unmöglich makroskopisch fast immer Stärke |F | für 2 Protonen Neutralisation Die Fähigkeit, Ladung zu tragen (Kapazität C) Lorentz-Kraft |F!C | = fc Q·q r2 " ! ! + !v × B ! F! = q E ! Q q " $& $% r Q=CU Lorentz-Kraft Lorentz-Kraft genügt, wenn die Ladungen ruhen " ! ! + !v × B ! F! = q E # ! " $& $% wenn sich Ladungen bewegen: Komplikationen wegen Zeitverzögerungen, Beschleunigungen ! Elektrodynamik : Darstellung nicht über ein Kraftgesetz Der andere Blickwinkel braucht den Feldbegriff HHelm, EXII SS2007 Freiburg ! Felder Skalares Feld Vektorfeld • Bisher Felder definiert über die Kraft • Das Feld gibt es auch, wenn keine Probeladung vorhanden ist • Feldgrößen im Raum • Graphisch als Vektor • Feldlinie : Darstellung eines Vektorfeldes Darstellung eines Vektorfeldes HHelm, EXII SS2007 Freiburg Tangente an Feldvektoren !v (x, y, z, t) • abstrakte Funktion : Darstellung eines Vektorfeldes • Fluss (Fluss aus einem Volumen) Eigenschaften eines Vektorfeldes Eigenschaften eines Vektorfeldes • Fluss (Fluss aus einem Volumen) mittlere Normalkomponente x Oberfläche HHelm, EXII SS2007 Freiburg ! ! ! ! • Zirkulation mittlere Normalkomponente x Oberfläche Eigenschaften eines Vektorfeldes ! , $--. / 0 -$% & * 1 2 % & -3 2 2 1 ) 1 4 ( 05 1 "# $% & '( ) * ! ! ! + + • Zirkulation mittlere Tangentialkomponente x Umfang + • Zirkulation mittlere Tangentialkomponente x Umfang HHelm, EXII SS2007 Freiburg Gesetze der Elektrodynamik (1) ! ! ! ! div !v • • ! · !v ∇ “nabla” Fluss (Vorzeichen, Betrag) ! ! durch Der Fluss von E eine geschlossene Oberfläche = (1/"0 )× (Nettoladung innen) Zirkulation (Vorzeichen, Betrag, Richtung) !" ! + − ! rot !v &% ' ( ! × !v ∇ ! " # $% &)* ' ' +, wenn keine Ladungen drin sind, dann ist die mittlere Normalkomponente auf der geschlossenen Oberfläche gleich Null ! curl Gesetze der Elektrodynamik (2) Gesetze der Elektrodynamik (3) & ! Zirkulation von E entlang der Kurve C = − dtd (Fluss von B! durch S) ! " # $" % ! durch Der Fluss von B eine geschlossene Oberfläche ist gleich Null ! ! ! C ist eine geschlossene Kurve im Raum C bildet die Umrandung der Fläche S S darf beliebig gewölbt sein “quellenfrei” HHelm, EXII SS2007 Freiburg Gesetze der Elektrodynamik (4) ! entlang C) c2 × (Zirkulation von B d = dt (Fluss von E! durch S) + 1 !0 ×(Fluss des elektrischen Stromes durch S) Gesetze der Elektrodynamik (5) Lorentz-Kraft " ! ! ! ! F = q E + !v × B # % ! ! " #! $ " $& ! & $% ! Die 4 Maxwell Gleichungen + die Lorentz Kraft Maxwell - Gleichungen differentielle Form James Clerk Maxwell (1831-1879) • Hendrik Lorentz (1853-1928) 1 ! ·E ! = 1ρ ∇ "0 2 ! ! ×E ! = − ∂B ∇ ∂t 3 ! ·B ! =0 ∇ 4 ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t Der Rest der Vorlesung handelt von der Anwendung dieser fünf Gesetze !" ! ρ= c2 = (!0 µ0 ) −1 HHelm, EXII SS2007 Freiburg ! Σq V Ladungsträgerdichte Maxwell - Gleichungen Maxwell - Gleichungen differentielle Form 1 2 ! ·E ! = 1ρ ∇ "0 differentielle Form & 1 ! ·E ! = 1ρ ∇ "0 2 ! ! ×E ! = − ∂B ∇ ∂t ! ! ! ×E ! = − ∂B ∇ ∂t " # $" % ! ! ! 3 ! ·B ! =0 ∇ 3 ! ·B ! =0 ∇ 4 ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t 4 ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t c2 = (!0 µ0 ) c2 = (!0 µ0 ) −1 −1 Maxwell - Gleichungen Maxwell - Gleichungen differentielle Form 1 ! ·E ! = 1ρ ∇ "0 differentielle Form differentielles Volumen 1 ! ·E ! = 1ρ ∇ "0 2 ! ! ×E ! = − ∂B ∇ ∂t 2 ! ! ×E ! = − ∂B ∇ ∂t 3 ! ·B ! =0 ∇ 3 ! ·B ! =0 ∇ 4 ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t % 4 ! " #! $ ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t & !" ! ! 2 c2 = (!0 µ0 ) c = (!0 µ0 ) −1 −1 HHelm, EXII SS2007 Freiburg ! ! ! Satz von Gauss (Fluss) Maxwell - Gleichungen differentielle Form & ! ! " # ! · dS != E S ! ·E ! dV ∇ V beliebige geschlossene Oberfläche $ " # $" % 1 ! ·E ! = 1ρ ∇ "0 2 ! ! ×E ! = − ∂B ∇ ∂t ! das darin enthaltene Volumen % ! " #! $ & 3 ! ·B ! =0 ∇ 4 ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t ! ! E ! dS differentielles Flächenelement c2 = (!0 µ0 ) −1 Satz von Stokes (Zirkulation) Maxwell - Gleichungen integrale Form ! ! · d!s = E C " # $ ! ! ! ∇ × E · dS 1 S 2 beliebige geschlossene Kurve ! ×E ! ∇ eine damit aufgespannte Fläche 3 d!s ! ·E ! = 1ρ ∇ "0 ! ! ×E ! = − ∂B ∇ ∂t ! ·B ! =0 ∇ S 4 ! dS " ! · dS != 1 ρ dV E "0 S " ! ! · dS ! ! · d!s = − d B E dt C ! ! · dS !=0 B ! differentielle Form " " ! · dS ! ! · d!s = µ0 !j · dS !+ 1 d E B c2 dt C ! ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t Die Gleichungen verknüpfen E und B (aber nur, wenn die Felder von der Zeit abhängen) HHelm, EXII SS2007 Freiburg Nabla Operator Vector Differential-Operator Konvention für mathematische Notation kartesisch: ! := ∇ ! := ∇ ! ∂ ∂ ∂ , , ∂x ∂y ∂z 3 ! i=1 !ei " = (∂x , ∂y , ∂z ) ∂ ∂xi Divergenz eines Vektorfeldes ! := ∇ ! · E(! ! r) = ∂x Ex + ∂y Ey + ∂z Ez div E Gradient eines skalaren Feldes f grad f ! f := ∇ = (∂x , ∂y , ∂z ) f = ! Gibt es Quellen oder Senken ? " ! " diese maximale · Zunahme ! = ∂f !ex + ∂f !ey + ∂f !ez ∇f ∂x ∂y ∂z Rotation eines Vektorfeldes ! rot E ! := ∇ ! · E(! ! r) = ∂Ex + ∂Ey + ∂Ez div E ∂x ∂y ∂z Ein Mass dafür, ob das Feld auf einen Punkt hin konvergiert. Einheitsvektor in Richtung der maximalen f -Zunahme ! × E(! ! r) ∇ (∂y Ez − ∂z Ey , ∂z Ex − ∂x Ez , ∂x Ey − ∂y Ex ) := = ! ×E ! = ∇ HHelm, EXII SS2007 Freiburg !ex !ey !ez ∂ ∂x ∂ ∂y ∂ ∂z Ex Ey Ez “Pseudo Determinante” Nabla Operator 12 Qualitative Experimente Produktregeln: Strom fliesst durch einen Draht, der über einem Stabmagneten hängt. Die Elektronen bewegen sich im Draht mit der Geschwindigkeit v. Wegen ! g) = f ∇g ! + g ∇f ! ∇(f ! · (f!v ) = f ∇ ! · !v + !v · ∇f ! ∇ ! F! = q!v × B ! × (f!v ) = (∇f ! ) × !v + f ∇ ! × !v ∇ ) + werden sie abgelenkt und übertragen Impuls auf den Draht. Der Draht bewegt sich. ! , ! " #$ % & ! ' ( ! · (!u × !v ) = !v · (∇ ! × !u) − !u · (∇ ! × !v ) ∇ ..... * Qualitative Experimente (2) Warum bewegt sich auch der Magnet? 4. Gesetz : Strom durch einen Leiter, ! "= 0 bedeutet: → rot B Das Magnetfeld, das durch den stromführenden Draht erzeugt wird, übt Kraft auf Stabmagneten aus. 1 Qualitative Experimente (3) ) *+ ,- . /0 Zwei Drähte, jeder führt Strom. Jeder Draht bewirkt ein Magnetfeld am Ort des anderen Drahtes. Die Drähte ziehen sich an, wenn der Strom in dieselbe Richtung fließt. ! 2 3 #$ % & ! ' ( ! " HHelm, EXII SS2007 Freiburg ! # " $ # " % Qualitative Experimente (4) Ströme und Magnete bewirken magnetische Felder. Ein Strom entspricht einer bewegten Ladung. Wenn wir den Magneten im ersten Experiment durch eine stromdurchflossene Spule ersetzen, & erhalten wir das gleiche Ergebnis. '! " # $% ( Qualitative Experimente (5) ) ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t Die Zirkulation ist dieselbe für jede beliebige Schleife, die den stromführenden Draht einschließt. ! # $ & ! + ,-. / ! ! " # $% ! ,-. / * Qualitative Experimente (6) Das Magnetfeld eines Eisenstabes hat als Ursache auch bewegte Ladungen. Woher kommen diese Ströme? Vorstellung: von der Bewegung der Elektronen auf atomaren Bahnen. magnetisches Moment des Elektrons oder des Atomkerns beobachtbar! ⇒ # % ! · d!s B = const. 2πr1 B1 = B(r) ∝ ! " 2πr2 B2 = const. 1 r Qualitative Experimente (7) 3. Gesetz: Es gibt keine magnetischen Ladungen. Bei Teilung eines Magneten entstehen zwei neue Magneten, ! = 0. div B " " ! Wenn die atomaren Momente ungeordnet sind, ergibt sich kein Nettoeffekt. Bei mikroskopischer Ordnung ergibt sich eine makroskopische Magnetisierung. ! " ! Alle Magnete haben als Ursache einen elektrischen Strom. HHelm, EXII SS2007 Freiburg Qualitative Experimente (8) Qualitative Experimente (8) Wir laden einen Kondensator auf indem wir den Schalter schließen. Ein Strom I fließt für einige Zeit, obwohl der Stromkreis durch den Kondensator “unterbrochen”ist. ! entlang C) ∝ (Fluß von I durch S1 ) (Zirkulation von B C ! ! " # ! # # # ! $ % " $ S2 # " Qualitative Experimente (8) Qualitative Experimente (8) ! entlang C) ∝ (Fluß von I durch S1 ) (Zirkulation von B ! ! entlang C) ∝ (Fluß von I durch S1 ) (Zirkulation von B ! ! " # % ! " # # # $ # # # # $ % % " $ " $ % Wir zeichnen eine neue Oberfläche S2 , mit der gleichen Berandung C. Diese Fläche schneidet den Leiter nicht, sie schließt sich zwischen den Kondensatorflächen. Kein herkömmlicher Strom fließt durch diese Oberfläche, ! um die Kurve C muß die Gleiche bleiben. aber die Zirkulation von B Maxwell: Im Kondensator baut sich ein elektrisches Feld auf. ! entlang C) (Zirkulation von B ∝ ∂ ∂t % ! durch S2 ) (Fluss von E Zeitliche Änderung des elektrischen Feldes bewirkt magnetische Effekte HHelm, EXII SS2007 Freiburg Qualitative Experimente (9) Qualitative Experimente (10) Jetzt bewegen wir den Magneten und finden ebenso einen Strom, also bewegen sich die Ladungen. ! Wer bewegt die ruhenden Ladungen? → F! = q E. Woher kommt das elektrische Feld? Die geschlossene Leiterschleife mit dem Amperemeter bildet die Kurve C und spannt eine Fläche S auf. Wir bringen ein Strommeßgerät in den Leiterkreis. Jetzt bewegen wir den Draht im Magnetfeld. Wegen ! F! = q!v × B bewegen sich die Elektronen im Draht und wir beobachten einen Strom ! entlang C ) ∝ ∂ (Fluss von B ! durch S) ( Zirkulation von E ∂t * +$ % & ' ( ), -. " ) * +$ % & ' ( ), / -. " ) ! / ! ! " #$ % & ' ( ) ! " #$ % & ' ( ) ! ! Qualitative Experimente (11) Maxwell - Gleichungen integrale Form Wir schicken durch den Draht einen Wechselstrom I = I0 sin ωt. Mit einer Kombination von 2. + 4. Gesetz lässt sich die Entstehung elek" und B " tromagnetischer Wellen erklären. Wellen bedeutet hier: Die Felder E bewegen sich mit Lichtgeschwindigkeit c von unserer Antenne weg. Wo steckt −1 in den Maxwell Gleichungen die Lichtgeschwindigkeit? → c2 = (#0 µ0 ) 1 2 3 " ! · dS != 1 ρ dV E "0 S " ! ! · dS ! ! · d!s = − d B E dt C ! ! · dS !=0 B ! differentielle Form ! ·E ! = 1ρ ∇ "0 ! ! ×E ! = − ∂B ∇ ∂t ! ·B ! =0 ∇ S ! !" !! " ## $% ! !& ' 4 " " ! · dS ! ! · d!s = µ0 !j · dS !+ 1 d E B c2 dt C ! ! ! ×B ! = µ0 !j + 1 ∂ E ∇ c2 ∂t Die Gleichungen verknüpfen E und B (aber nur, wenn die Felder von der Zeit abhängen) HHelm, EXII SS2007 Freiburg HHelm, EXII SS2007 Freiburg











