Fourierreihen und Filter

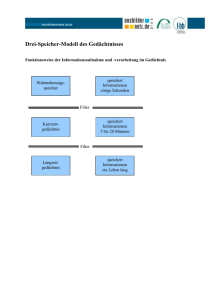
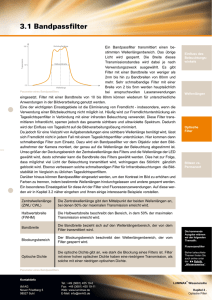
Gemeinsames
Grundpraktikum
Fourierreihen und Filter
Versuch-Nr.:
E404
Ziel: Der Laborversuch „Fourierreihen und Filter“ beschäftigt sich mit Fourierreihen und
Filtern und deren messtechnischer Untersuchung.
Inhaltsverzeichnis
1 Einleitung
1
2 Grundlagen
2.1 Periodische Signale und Fourierreihen
2.2 Der Reihenschwingkreis . . . . . . . .
2.2.1 Eingeschwungener Zustand . .
2.2.2 Einschwingverhalten . . . . .
2.3 Analoge Filter . . . . . . . . . . . . .
2.3.1 Grundtypen . . . . . . . . . .
2.3.2 RC-Tiefpass . . . . . . . . . .
1
1
2
2
5
7
7
7
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Aufgaben zur Versuchsvorbereitung
10
4 Versuchsdurchführung
4.1 Verwendete Geräte . . . . .
4.2 Synthese einer Rechteckfolge
4.3 Reihenschwingkreis . . . . .
4.4 RC-Tiefpass . . . . . . . . .
4.5 Anregung der Netzwerke mit
12
12
12
14
15
16
. . . . .
. . . . .
. . . . .
. . . . .
Signalen
. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .
unterschiedlicher Wellenform
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A Bedienung des Frequenzsythesizers
18
Literaturverzeichnis
19
Stand: 18. April 2013
E404: Fourierreihen und Filter
1
Einleitung
In diesem Versuch soll das Auftreten von Resonanzerscheinungen in einfachen elektrischen Netzwerken untersucht werden. Schwingungsfähige Netzwerke haben sowohl in der
Energietechnik als auch in der Nachrichtentechnik große Bedeutung. In der Energietechnik liegt ihr Einsatzgebiet vor allem in der Steuerung bzw. Kompensation der von den
Verbrauchern aufgenommenen Blindleistung, in der Nachrichtentechnik werden ihre frequenzselektiven Eigenschaften zur Herstellung von Filtern und Anpassungsschaltungen
ausgenutzt.
Fourierreihen und die Fourier-Transformation sind wichtige Werkzeuge in der Nachrichtentechnik und Systemtheorie. In diesem Versuch sollen periodische Signale mit unterschiedlichen Wellenformen synthetisiert und gefiltert werden.
2
2.1
Grundlagen
Periodische Signale und Fourierreihen
Ein im Allgemeinen komplexes Signal s(t) heißt periodisch, wenn es eine reelle Konstante
T gibt, so dass
s(t + T ) = s(t),
∀t
(1)
gilt. Die Konstante T wird stets positiv angenommen, und die kleinste solche Konstante,
für die Gleichung (1) gilt, ist die Periode des Signals. Jedes Signal s(t), das Gleichung (1)
erfüllt, kann durch eine Fourierreihe der Form
∞
s(t) =
a0 X
(ak cos kω0 t + bk sin kω0 t)
+
2
k=1
(2)
beschrieben werden. Hierbei ist ω0 = 2π
die Grundkreisfrequenz bzw. f0 = T1 die GrundT
frequenz von s(t). Die sogenannten Fourierkoeffizienten ak und bk berechnen sich nach
2
ak =
T
Zt+T
s(t) cos kω0 tdt ,
(3)
s(t) sin kω0 tdt .
(4)
t
2
bk =
T
Zt+T
t
Die Superposition von Kosinus- und Sinusschwingungen gewichtet mit den entsprechenden
Fourierkoeffizienten beschreibt die Ausgangsfunktion s(t). Dominierend sind dabei diejenigen Schwingungen, deren Fourierkoeffizienten betragsmäßig sehr groß sind. Die komplexe
Form der Fourierreihe lautet
1
E404: Fourierreihen und Filter
s(t) =
+∞
X
ck ejkω0 t
.
(5)
k=−∞
Das mit T periodische Signal s(t) kann also als lineare Überlagerung von komplexen
Exponentialschwingungen mit der Grundschwingung ω0 und den Harmonischen kω0 beschrieben werden. Die komplexen Exponentialschwingungen werden mit den komplexen
Koeffizienten
1
ck =
T
Zt+T
s(t)e−jkω0 t dt
(6)
t
gewichtet. Diese Form der Darstellung von s(t) lässt erkennen, welche Frequenzen im
Signal auftreten und wie stark sie gewichtet sind.
2.2
Der Reihenschwingkreis
Das einfachste elektrische schwingfähige System enthält einen Kondensator als Speicher
für elektrische Feldenergie und eine Spule als Speicher für magnetische Feldenergie. Beide
Speicher können über Verbindungsleitungen Energie untereinander austauschen. Die in
elektrischen Schwingkreisen auftretenden Energieverluste entstehen oft maßgeblich durch
den ohmschen Widerstand der Spulenwicklung. Sie werden im Ersatzschaltbild durch
einen Widerstand Rs berücksichtigt, der mit der Induktivität in Reihe geschaltet ist. Die
in Spulen und Kondensatoren auftretenden Magnetisierungs- und Dielektrizitätsverluste
sind gegenüber den Stromwärmeverlusten oft sehr klein und sollen in diesem Versuch
vernachlässigt werden. Die Grundformen elektrischer Schwingkreise sind der Reihen- und
der Parallelschwingkreis, bei denen die Energiespeicher L und C in Reihe oder parallel
geschaltet sind. In diesem Versuch soll der Reihenschwingkreis näher untersucht werden.
2.2.1
Eingeschwungener Zustand
Abbildung 1 zeigt das Ersatzschaltbild eines mit einer sinusförmigen Spannung U gespeisten Reihenschwingkreises.
Befindet sich dieser im eingeschwungenen Zustand, so lässt sich die komplexe Wechselstromrechnung anwenden, und man erhält für die Impedanz des Reihenschwingkreises
Z = |Z|ejφ = Rs + jωL +
1
jωC
,
(7)
wobei sich Betrag und Phase der Impedanz nach
s
|Z| =
1
Rs2 + ωL −
ωC
2
2
(8)
E404: Fourierreihen und Filter
Abbildung 1: Ersatzschaltbild des Reihenschwingkreises
und
φ = arctan
1
ωL − ωC
Rs
(9)
berechnen lassen. Der Verlauf der Impedanz Z in Abhängigkeit von der Kreisfrequenz ω
kann als Ortskurve in der komplexen Ebene dargestellt werden (siehe Abbildung 2).
Abbildung 2: Ortskurve der Impedanz des Reihenschwingkreises
Dieser Darstellung lassen sich die wesentlichen Betriebseigenschaften entnehmen. Als Resonanzkreisfrequenzen ω0 wird die Kreisfrequenz definiert, bei der der Betrag der Impedanz der Spule gleich dem des Kondensators ist, in diesem Fall ist der Blindwiderstand
3
E404: Fourierreihen und Filter
minimal. Der hier betrachtete Reihenschwingkreis hat demnach eine Resonanzfrequenz
von
ω0 = √
1
LC
.
(10)
Betrachtet man eine sinusförmige anregende Spannung U = U0 ej0 , so ist der Strom I
durch
I=
U0
Z
(11)
gegeben. Der Amplituden- und Phasenverlauf des Stromes ist in Abbildung 3 dargestellt.
Abbildung 3: Qualitativer Verlauf von Amplitude und Phase des Stromes
Die Bandbreite des Reihenschwingkreises ist durch den Abfall des Amplitudenverlaufs
auf den √12 -fachen Wert des Maximums oder durch die 45◦ -Punkte des Phasenverlaufs
gegeben. Die Bandbreite kann auch durch den Gütefaktor Q ausgedrückt werden:
B=
∆ω
f0
=
2π
Q
.
(12)
Der Gütefaktor gibt das Verhältnis von der in den Energiespeichern L bzw. C gespeicherten Blindenergie zur im Widerstand in Wärme umgesetzten Energie an:
Q = 2π
gespeicherte Energie
pro Periode verbrauchte Energie ω=ω0
.
(13)
Im Resonanzfall ist die Blindenergie für einen Zeitpunkt vollständig induktiv, für einen
anderen Zeitpunkt vollständig kapazitiv gespeichert. Der Gütefaktor kann auch aus dem
Verhältnis der Spannung am Kondensator bzw. an der Spule zur Klemmenspannung bestimmt werden:
4
E404: Fourierreihen und Filter
r
|U C | L
1
1
|U L | ω0 L
Q=
=
=
=
=
|U | ω=ω0 |U | ω=ω0
Rs
ω0 CRs
Rs C
(14)
Die Spannungen am Kondensator und an der Spule können in Resonanznähe erheblich
größer als die Klemmenspannung sein. Die Spannungsmaxima treten an den einzelnen
Reaktanzen bei Frequenzen auf, die sich von der Resonanzkreisfrequenz unterscheiden.
Die Spannungen an der Spule und am Kondensator lassen sich nach
j ωω0 Q
UL =
1 + jQ ωω0 −
ω0
ω
−j ωω0 Q
1 + jQ ωω0 −
ω0
ω
U
(15)
U
(16)
und
UC =
bestimmen.
2.2.2
Einschwingverhalten
In diesem Abschnitt soll untersucht werden, wie sich die Spannungen und der Strom im
Reihenschwingkreis verhalten, wenn zum Zeitpunkt t = t0 eine Spannung u(t) angelegt
wird. Abbildung 4 zeigt das entsprechende Ersatzschaltbild.
Abbildung 4: Ersatzschaltbild des Reihenschwingkreises mit sprungförmiger Anregung
Die Differentialgleichung für den Strom i(t) läßt sich aus der Maschengleichung gewinnen:
5
E404: Fourierreihen und Filter
1
C
Z
idt + Rs i + L
di
=u
dt
(17)
Durch Differenzierung erhält man
di
d2 i
du
+ LC 2 = C
dt
dt
dt
und die zugehörige homogene Differentialgleichung
i + Rs C
i+
(18)
1 d2 i
2D di
+ 2 2 =0 ,
ω0 dt ω0 dt
(19)
1
wobei ω0 = √LC
die Eigenfrequenz des Kreises und D = ω0 R2 s C die Dämpfung ist. Die
allgemeine Lösung der inhomogenen Differentialgleichung setzt sich aus einer Überlagerung der Lösung der homogenen Differentialgleichung ih (t) und einer speziellen Lösung
der inhomogenen Differentialgleichung istat (t) zusammen:
i(t) = ih (t) + istat (t) .
(20)
Die Lösungen der homogenen Differentialgleichung lauten für schwache (D < 1), kritische
(D = 1) und starke (D > 1) Dämpfung:
h
√
√
i
2
2
ih (t) = A1 sin
1 − D ω0 t + A2 cos
1 − D ω0 t e−Dω0 t ,
ih (t) = [B1 + B2 t] e−Dω0 t , D = 1
h
i
√
√
2
2
ih (t) = C1 eω0 t D −1 + C2 e−ω0 t D −1 e−Dω0 t ,
D<1
(21)
(22)
D>1 .
(23)
Die Konstanten A1 , A2 , B1 , B2 , C1 und C2 sind Integrationskonstanten.
Für 0 < D < 1 beschreibt die Lösung der homogenen Differentialgleichung eine Sinusschwingung mit exponentiell abklingender Amplitude. Für D > 1 ist die Lösung eine
exponentiell abklingende Zeitfunktion. Der Kreis ist in diesem Falle nicht schwingfähig.
Um die allgemeine Lösung der inhomogenen Differentialgleichung zu erhalten, muss der
Lösung der homogenen Differentialgleichung eine spezielle Lösung istat überlagert werden.
Diese lässt sich finden, indem man den Zeitpunkt t → ∞ betrachtet und eine Berechnung mittels komplexer Wechselstromrechnung durchführt. Zu diesem Zeitpunkt ist der
Einschwingvorgang abgeklungen und es fließt nur noch istat .
Da die Spannung am Kondensator und der Strom durch die Spule als stetig vorausgesetzt
sind, können mittels der Anfangsbedingungen
uC (t0 − 0) = uC (t0 + 0)
(24)
iL (t0 − 0) = iL (t0 + 0)
(25)
6
E404: Fourierreihen und Filter
die Integrationskonstanten bestimmt werden.
2.3
2.3.1
Analoge Filter
Grundtypen
Mit Hilfe analoger Filter lassen sich die Frequenzanteile eines Signals gezielt beeinflussen.
Grundsätzlich werden vier Filtergrundtypen unterschieden:
• Tiefpassfilter
• Hochpassfilter
• Bandpassfilter
• Bandsperrfilter
Die Bezeichnungen der Filter geben jeweils an, welche Frequenzanteile des Signals am
Eingang des Filters weitgehend ungehindert auf den Ausgang übertragen werden (Durchlassbereich) und welche gedämpft werden (Sperrbereich). In Abbildung 5 sind die idealen Betragsfrequenzgänge A(f ) für die vier Filtergrundtypen dargestellt. Der Betragsfrequenzgang ist das frequenzabhängige Amplitudenverhältnis von Ausgangs- und Eingangssignal. Die Frequenz fg , bei der der Übergang vom Durchlassbereich zum Sperrbereich
erfolgt, wird als Grenzfrequenz bezeichnet.
Der Betragfrequenzgang wird in der Nachrichtentechnik häufig logarithmisch in Dezibel
(dB) angegeben:
AdB (f ) = 20 log10 A(f ) .
(26)
Als Grenzfrequenz fg wird üblicherweise diejenige Frequenz bezeichnet, bei der die Dämpfung des Filters 3dB beträgt:
1
A(fg ) = √
2
AdB (fg ) = −3dB,
2.3.2
.
(27)
RC-Tiefpass
Reale(d. h. ohne abrupten Übergang zwischen Durchlass- und Sperrbereich), passive Filter
lassen sich durch Schaltungen bestehend aus Spulen, Kondensatoren und Wirkwiderständen realisieren. Im Folgenden soll ein passiver Tiefpassfilter erster Ordnung in Form eines
RC-Gliedes wie in Abbildung 6 dargestellt betrachtet werden.
Der komplexe Frequenzgang des Filters A(f ) lässt sich mittels komplexer Wechselstromrechnung bestimmen:
A(f ) =
UY
1
=
UX
1 + j2πf RC
7
.
(28)
E404: Fourierreihen und Filter
Abbildung 5: Betragsfrequenzgänge der vier Filtergrundtypen
Abbildung 6: RC-Tiefpassfilter 1. Ordnung
Der komplexe Frequenzgang lässt sich in Betragsfrequenzgang und Phasengang zerlegen:
1
|A(f )| = p
1 + (2πf RC)2
P (f ) = − arctan 2πf RC
,
.
(29)
(30)
Die 3dB Grenzfrequenz fg des RC-Gliedes berechnet sich mit Hilfe der Gleichungen (27)
und (28) zu
fg =
1
2πRC
8
.
(31)
E404: Fourierreihen und Filter
Das Frequenzverhalten von Filtern lässt sich mit dem Bode-Diagramm veranschaulichen.
In dieser grafischen Darstellung wird der Betragsfrequenzgang in Dezibel und der Phasenfrequenzgang über der logarithmierten Frequenz f aufgetragen.
Abbildung 7: Bodediagramm des RC-Tiefpassfilters
In Abbildung 7 ist das Bode-Diagramm des RC-Gliedes mit normierter Frequenzachse
dargestellt. Die Abbildung zeigt, dass sich der Betragsfrequenzgang im Bodediagramm
durch zwei Asymptoten annähern lässt. Der Bereich f fg kann durch eine waagerechte
Asymptote angenähert werden. Für f fg kann die Dämpfung durch eine Asymptote mit
der Steigung -20 dB/Dekade beschrieben werden. Eine stärkere Dämpfung im Sperrbereich
lässt sich beispielsweise mit Hilfe von Filtern höherer Ordnung realisieren.
9
E404: Fourierreihen und Filter
3
Aufgaben zur Versuchsvorbereitung
Hinweis: Die Aufgaben sind während der Versuchsvorbereitung (zu Hause) zu
lösen!
1. Bestimmen Sie die reellen Fourierkoeffizienten der abgebildeten Signale aus Abbildung 8. Geben Sie Zahlenwerte für die ersten sechs von Null verschiedenen Reihenglieder von Dreieck- und Rechteckfolge an. Die Werte für die Amplituden finden Sie
in Kapitel 4.2.
Raum für Ihre Berechnungen (Durchführung zu Hause)
2. Zeichnen Sie qualitativ die Ortskurven der Impedanz und Admittanz eines gedämpften Reihenschwingkreises und eines gedämpften Parallelschwingkreises. Beschriften
Sie die Ortskurven sinnvoll.
10
E404: Fourierreihen und Filter
Raum für Ihre Skizzen (Durchführung zu Hause)
3. Zeichnen Sie das Ersatzschaltbild eines Hochpasses bestehend aus Kondensator und
Wirkwiderstand bzw. aus Spule und Wirkwiderstand. Für die Realisierung welcher
Filtergrundtypen eignet sich ein Schwingkreis?
Raum für Ihre Antworten (Durchführung zu Hause)
11
E404: Fourierreihen und Filter
Abbildung 8: Drei Zeitsignale mit unterschiedlicher Wellenform
4
Versuchsdurchführung
4.1
1
1
1
2
1
1
Verwendete Geräte
Zweikanaloszilloskop (Tektronix „TDS 2002B“)
Frequenzsynthesizer (Beschreibung im Anhang)
Funktionengenerator
Vielfachmessgeräte
Netzgerät
Schaltbrett und diverse Bauteile
4.2
Synthese einer Rechteckfolge
In diesem Teil soll die im Vorbereitungsteil dargestellte Rechteckfolge s3 (t) mit Hilfe ihrer
ersten 6 von Null verschiedenen Reihenglieder approximiert werden. Dazu soll S3 = 7V
gelten.
1. Stellen Sie zunächst alle Reihenglieder einzeln am Synthesizer ein. Verwenden Sie
zum genauen Arbeiten die Funktion CURSOR auf dem Oszilloskop.
2. Greifen Sie die ersten drei Reihenglieder am Summationsausgang des Synthesizer
ab, und stellen Sie sie auf dem Oszilloskop dar. Korrigieren sie die Phasenwinkel,
falls erforderlich.
3. Summieren Sie nun nacheinander Reihenglieder phasenrichtig hinzu, und beobachten Sie das Oszillographenbild. Welche Veränderungen beobachten Sie bei jedem
weiteren zugeschalteten Reihenglied?
12
E404: Fourierreihen und Filter
Raum für Ihre Antworten
4. Bestimmen Sie die Grundfrequenz der Rechteckfolge und erzeugen Sie mit dem
digitalen Funktionsgenerator ein Rechtecksignal gleicher Amplitude und Frequenz.
5. Wechseln sie in des MATH MENU und führen sie eine FFT (Fast-FourierTransformation) durch. Für Fenster wählen Sie „Flattop “und für den FFT-Zoom
wählen Sie „1x“. Vergleichen Sie die beiden Signale und erklären Sie die Unterschiede.
Raum für Ihre Antworten
13
E404: Fourierreihen und Filter
4.3
Reihenschwingkreis
In diesem Versuchsteil soll der Reihenschwingkreis im eingeschwungenen Zustand charakterisiert werden. Die unbekannte Induktivität ist später aus den Messwerten zu bestimmen.
1. Ermitteln Sie messtechnisch die Resonanzfrequenz des Schwingkreises. Nehmen Sie
für |U | = 0, 5V den Amplitudenverlauf I(f ) für geeignete Frequenzen auf (s. Abbildung 9). Die Spannung |U | muss konstant gehalten werden, indem die Generatorspannung entsprechend angepasst wird. Die Schaltung verhält sich dann so, als
würde der Schwingkreis von einer idealen Spannungsquelle gespeist werden. Ermitteln Sie obere und untere Grenzfrequenz.
Raum für Ihre Antworten
2. Bestimmen Sie die Induktivität L.
14
E404: Fourierreihen und Filter
Raum für Ihre Antworten
3. Bestimmen Sie die Güte Q.
Raum für Ihre Antworten
Abbildung 9: Versuchsaufbau zur Bestimmung von I nach Betrag und Phase
4.4
RC-Tiefpass
Es ist das Übertragungsverhalten eines Tiefpassfilters erster Ordnung zu untersuchen.
1. Bauen Sie ein Tiefpassfilter nach Abbildung 6 mit R = 1kΩ und C = 0, 1µF auf.
15
E404: Fourierreihen und Filter
2. Berechnen Sie die Grenzfrequenz fg für das Tiefpassfilter.
Raum für Ihre Antworten
3. Ermitteln Sie den Betragsfrequenzgang A(f ) für geeignete Frequenzpunkte. Verwenden Sie als Eingangssignal ein Sinussignal mit geeigneter Amplitude und variabler
Frequenz und oszillographieren Sie Ein- und Ausgangssignal des Filters. Ermitteln
Sie aus dem Amplitudenverhältnis von Ein- und Ausgangssignal für jede Frequenz
die Verstärkung A(f ) und stellen Sie sie in einem doppelt logarithmischen Diagramm
dar. Ermitteln Sie graphisch die Grenzfrequenz.
Raum für Ihre Antworten
4.5
Anregung der Netzwerke mit Signalen unterschiedlicher Wellenform
1. Speisen sie den Tiefpass mit einem Rechteck- und einem Dreiecksignal der Frequenz
f = 10kHz. Vertauschen Sie die Bauteile und speisen Sie den Hochpass mit einem
Rechteck- und einem Dreiecksignal der Frequenz f = 100Hz. Beschreiben Sie die
16
E404: Fourierreihen und Filter
Ausgangssignale. Welcher mathematische Zusammenhang besteht? (kurze Beschreibung)
Raum für Ihre Antworten
2. Tauschen Sie den Kondensator des Tiefpasses in einen Parallelschwingkreis aus den
Bauteilen des Reihenschwingkreises. Speisen Sie mit unterschiedlichen Wellenformen
und Frequenzen. Welches Verhalten ist zu beobachten?
Raum für Ihre Antworten
17
E404: Fourierreihen und Filter
A
Bedienung des Frequenzsythesizers
18
E404: Fourierreihen und Filter
Literatur
[1] Ameling: Grundlagen der
schweig/Wiesbanden, 1984.
Elektrotechnik
I
und
II;
Vieweg;
Braun-
[2] Bronstein, K. A. Semendjajew: Taschenbuch der Mathematik; Verlag Harri Deutsch,
Frankfurt a.M., 1987.
19