Hinweise zum Vorgehen bei Stochastik Aufgaben

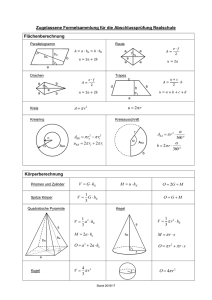
Hinweise zur Wahrscheinlichkeitstheorie
Vorgehen beim Lösen von Aufgaben
Bei Komplexeren Wahrscheinlichkeitstheorie-Aufgaben muss man zuerst folgende
Überlegungen machen:
1. Handelt es sich bei der gesuchten Wahrscheinlichkeit um eine
Wahrscheinlichkeit von zwei oder mehr Ereignissen, die sich gegenseitig
ausschliessen?
Falls ja, wird sich die Lösung aus zwei oder mehreren Summanden
zusammensetzen: P(A ∩ B) = P(A) + P(B)
Z.B. beim Münzwurf: P(Kopf oder Zahl) = P(Kopf) + P(Zahl)
2. Lässt sich die Wahrscheinlichkeit des Gegenereignisses einfacher berechnen
als die gesuchte Wahrscheinlichkeit?
Falls ja, wird die Komplementärregel verwendet. P(A) = 1 – P(Ag)
(Dabei ist Ag das Gegenereignis von A.) Die Wörter "mindestens" oder
"höchstens" können darauf hindeuten, dass die Verwendung der
Komplementärregel sinnvoll sein könnte.
Weiter muss man sich überlegen, ob die Wahrscheinlichkeit eines mehrstufigen
Experimentes gesucht wird:
• Falls ja: Die Wahrscheinlichkeit kann mit Hilfe eines Baumdiagrammes (oder
mit der Vorstellung eines Baumdiagrammes) berechnet werden. Allenfalls
kann dabei die Formel von Bernoulli verwendet werden.
• Falls nein: Die Wahrscheinlichkeit wird mit Hilfe der Formel:
"günstige Ereignisse"/"mögliche Ereignisse" berechnet werden.
Folgende Überlegungen können bei der Berechnung der Anzahl Ereignissen helfen:
1. Eine genaue Analyse des Problems ist notwendig! Man macht nichts anderes
als Möglichkeiten zählen.
Schrittweises Lösen von komplexeren Problemen ist sinnvoll.
Die Kombinatorik-Formeln helfen beim Zählen, wenn einzelne Teilschritte des
Problems zu komplex werden, um es sich konkret vorzustellen oder
aufzuzeichnen.
2. Einzelne Wörter in der Formulierung der Aufgabe weisen darauf hin, ob die
einzelnen Teilergebnisse addiert oder multipliziert werden müssen. (Evtl. hilft
es, wenn man das Problem noch einmal neu formuliert und darauf achtet, wo
man "und" und wo man "oder" verwendet.)
a. "oder" weist darauf hin, dass die Zahlen addiert werden müssen.
b. "und" weist darauf hin, dass die Zahlen multipliziert werden müssen.
Nötige Theorie zu Aufgaben der Wahrscheinlichkeitstheorie:
Baumdiagramm:
1. Pfadregel: Die Wahrscheinlichkeit eines Elementarereignisses bei einem
mehrstufigen Zufallsexperiment ist gleich dem Produkt aller
Wahrscheinlichkeiten entlang des zugehörigen Pfades im Baumdiagramm.
2. Pfadregel: Die Wahrscheinlichkeit eines Ereignisses in einem mehrstufigen
Zufallsexperiment ist gleich der Summe der Wahrscheinlichkeiten der
einzelnen Pfade.
3. Regel (Verzweigungsregel): Die Summe aller Wahrscheinlichkeiten an den
Ästen, die von einem Punkt aus gehen, ist stets 1.
Kombinatorik:
n:= Anzahl der zur Auswahl stehenden Elemente
k:= Anzahl Elemente, welche ausgewählt werden sollen.
Mit Wiederholung
Mit Beachtung der
Reihenfolge
Ohne Beachtung
der Reihenfolge
nk
 n + k − 1 (n + k − 1)!
=

 k!(n − 1)!
k


Ohne Widerholung
n!
(n − k )!
n
n!
  =
 k  k!(n − k )!
Laplace-Regel
Für jedes Ereignis A gilt die Rechenregel:
Anzahl _ der _ für _ A _ günstigen _ Ergebnisse
P(A)=
Anzahl _ aller _ Ergebnisse
n!
n1!n2!⋅... ⋅ n p !
Hypergeometrische Verteilung
Werden einer Urne mit genau N Kugeln (W weisse, N-W schwarze) genau n Kugeln
auf einen Griff, also ohne Zurücklegen entnommen, dann gilt:
W  N − W 
 
 m n − m 


P(Es werden genau m weisse Kugeln entnommen)= 
N
 
 
n
Natürlich kann diese Formel auf andere Probleme übertragen werden – es müssen
nicht unbedingt Kugeln gezogen werden.
Bernoulli-Formel
Ein Zufallsexperiment heisst Bernoulli-Experiment, wenn es nur zwei Ergebnisse hat.
Ein Bernoulli-Experiment mit der Wahrscheinlichkeit p für Treffer werde n-mal
durchgeführt. Die Durchführungen seien unabhängig. Dann beträgt die
Wahrscheinlichkeit für genau k Treffer:
n
P(k Treffer)=   p k (1 − p ) n−k
k 