3.1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0 2 8 8 4

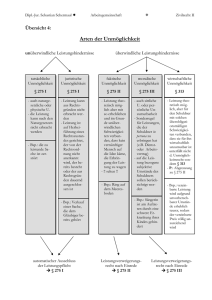
3.1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0 2 8 8 4 1 9
7 1 6 9 3 9K9ONSTRUIEREN
3 7 5 1 0 5 8 2 0 9MIT
7 4 9Z4IRKEL
4 5 9 2UND
3 0 7 L8INEAL
1 6 4 0−6 2 8 6 2 0
899862803482534211706798214808651328230
DIE KLASSISCHEN PROBLEME DER ANTIKE
664709384460955058223172535940812848111
VERSTÄNDLICH
ERKLÄRT
745028410270193852110555964462294895493
038196442881097566593344612847564823378
Die drei klassischen Probleme der Antike sind
6 7 8Konstruktionsprobleme,
3 1 6 5 2 7 1 2die
0 1mit9Zirkel
0 9 und
1 4Lineal
564856692346034861045
4 3 2unlösbar
6 6 4sind.
8 2Schon
1 3 die
3 9Griechen
3 6 0sind
7 2an6ihnen
0 2 4 9von
1 4 1Cyrill
2 7 3Scheidegger
72458700660
gescheitert; die Unmöglichkeit der drei Probleme
6 3 1wurde
5 5jedoch
8 8 1erst7 4
1 5 2 0 9bewiesen.
2 0 9 6 2Kantonsschule
8 2 9 2 5 4 0 Wiedikon
9171536436
im 8
19.8Jahrhundert
Meine Maturitätsarbeit hat das Ziel, die Thematik
7 8 9dieser
2 5 drei
9 0 Probleme
3 6 0 0 neu
1 1 aufzubereiten
3 3 0 5 3 0und5 4 8Betreut
8 2 0 4durch
6 6 5Markus
2 1 3 8Egli
414695
1 9 4verständlich
1 5 1 1zu6erklären.
0 9 4Dazu
3 3wird
0 5ausgehend
7 2 7 0vom3 6 5 7 5 9 5 9 1 9 5 3 0 9 2 1 8 6 1 1
Mittelschulstoff schrittweise das Wissen aufgebaut,
7 3 8welches
1 9 3notwendig
2 6 1 1 ist,
7 9um3 1die0 Beweise
5 1 1 8der5 4 8 0 7 4 4 6 2 3 7 9 9 6 2 7 4 9 5 6
Der
Weg
zu
den
Unmöglichkeitsbeweisen
Unmöglichkeit der Würfelverdoppelung und der
7 3 5Winkeldreiteilung
1 8 8 5 7 5 2zu7 2verstehen.
4 8 9 1 2Für2 7den9 3 8 1 8 3 0 1 1 9 4 9 1 2 9 8 3 3 6 7
Um die Unmöglichkeit der drei klassischen Probleme
3 3 6Unmöglichkeitsbeweis
2 4 4 0 6 5 6 6zur4Quadratur
3 0 8 6des
0 2Kreises
1 3 9 4zu9beweisen,
4 6 3 wird
9 5die2 Frage
2 4 nach
7 3der7 1Lösbarkeit
9070
eines bestimmten Problems auf die Frage
wird lediglich ein Denkanstoss gegeben.
2 1 7 9 8 6 0 9 4 3 7 0 2 7 7 0 5 3 9 2 1 7zurückgeführt,
1 7 6 2 9ob 3man1eine
7 6bestimmte
7 5 2Strecke/Zahl
38467
aus einer gegebenen Einheitslänge mit Zirkel und
4 8 1Die8Würfelverdoppelung
4 6 7 6 6 9 4 0 5 1 3 2 0 0 0 5 6 8Lineal
1 2 7konstruieren
1 4 5 2kann.
6 3 5Bei6 der
0 8 Würfel2778
verdoppelung ist diese Zahl 2 (Kantenlänge eines
Bei der Würfelverdoppelung
5 7 7(auch
1 3bekannt
4 2 7als5delisches
7 7 8 9 6 0 9 1 7 3 6 3 7Würfels
1 7 8mit7Volumen
2 1 42),6 bei
8 4der4Quadratur
0 9 0 1des2 2
Kreises
𝜋 (Seitenlänge des Quadrates mit
ist0 ein
Verfahren
4 9 5Problem)
3
4
3
1
4
6
5
4
9
5
8
5
3
7
1
0
5
0
7
9
2
2
7
9
6
8
9
2
5
8
9
2
3
5
4
Flächeninhalt 𝜋) und bei der Winkeldreiteilung
gesucht, einen Würfel im
2 0 1Volumen
9 9 5zu 6verdoppeln.
1 1 2 1Man2 9 0 2 1 9 6 0 8 6 4cos020°.
3441815981362977
will aus der gegebenen
Anschliessend erfolgt eine Charakterisierung der mit
Kantenlänge
eines
Würfels
mit
4 7 7 1 3 0 9 9 6 0 5 1 8 7 0 7 2 1 1 3 4 9Zirkel
9 9und9 Lineal
9 9 8konstruierbaren
3 7 2 9 7Strecken/Zahlen.
804995
einem bestimmten Volumen
geschieht
mithilfe
der
Gleichungen
von
Gerade
1 0 5die9Kantenlänge
7 3 1 7eines
3 2Würfels
8 1 6 0 9 6 3 1 8 5 9 5Dies
0
2
4
4
5
9
4
5
5
3
4
6
9
0
8
3
0
und Kreis in der Ebene. Es stellt sich heraus, dass alle
mit dem doppelten Volumen
(genauer
gesagt
alle0 0
2 6 4konstruieren.
2 5 2 2 3 0 8 2 5 3 3 4 4 6 8 5 0 3 5«Quadratwurzelausdrücke»
2
6
1
9
3
1
1
8
8
1
7
1
0
1
0
Zahlen, die sich aus den rationalen Zahlen durch
3 1 3Die7Winkeldreiteilung
8 3 8 7 5 2 8 8 6 5 8 7 5 3 3 2 0 8wiederholtes
3 8 1 4Anwenden
2 0 6 1der7vier1Grundoperationen
7766914
und des Ziehens der Quadratwurzel berechnen
7 3 0Bei3der5 Winkeldreiteilung
9 8 2 5 3 4ist9 0 4 2 8 7 5 5 4 6 8lassen)
7 3 konstruierbar
1 1 5 9 sind.
56286388235
ein allgemeines Verfahren
3 7 8gesucht,
7 5 9einen
3 7 5beliebigen
1 9 5 7 7 8 1 8 5 7 7 8 0Letztendlich
5 3 2 1muss
7 1also2bewiesen
2 6 8 werden,
0 6 6dass
1 3die0 0
im ersten Schritt hergeleiteten Zahlen nicht auch als
Winkel in drei gleich grosse
1 9 2Teile7zu8zerlegen.
7 6 6 1 1 1 9 5 9 0 9 2 1 6 4 2 0solche
1 9«Quadratwurzelausdrücke»
8 9 3 8 0 9 5 2 geschrieben
5 7 2 0wer106
den können. Für Würfelverdoppelung und Winkel5 4 8 5 8 6 3 2 7 8 8 6 5 9 3 6 1 5 3 3 8 1dreiteilung
8 2 7 9geschieht
6 8 2das3 0mit3 einem
0 1 9ähnlichen
5203
Ansatz. Es handelt sich jeweils um eine Verkettung
Die Quadratur des Kreises
5 3 0Bei1der8Quadratur
5 2 9 des
6 8Kreises,
9 9 5 7 7 3 6 2 2 5 9 9von4 verschiedenen
1 3 8 9 1Widerspruchsbeweisen.
2 4 9 7 2 1 7 Bei
7 5der2 8
Quadratur des Kreises müsste man weiter gehen.
3 4 7ist 9ein1Verfahren
3 1 5gesucht,
1 5 5aus7 4 8 5 7 2 4 2 4 5 4Ihre
1 5Unmöglichkeit
0 6 9 5 9folgt5 0aus8der2 9sogenannten
53311
einem gegebenen Kreis ein
Transzendenz von 𝜋 (eine Zahl heisst transzendent,
6 8 6Quadrat
1 7 2mit7 dem
8 5 gleichen
5 8 8 9 0 7 5 0 9 8 3 8 1wenn
7 5sie4nicht
6 3Lösung
7 4einer
6 4Polynomgleichung
9 3 9 3 1 9mit2 5
Flächeninhalt zu konstruieren.
Koeffizienten ist). Der Beweis der
5 0 6 0 4 0 0 9 2 7 7 0 1 6 7 1 1 3 9 0 0 9rationalen
8
4
8
8
2
4
0
1
2
8
5
8
3
6
1
6
0
Transzendenz von 𝜋 hätte den Rahmen meiner
3 5 6 3 7 0 7 6 6 0 1 0 4 7 1 0 1 8 1 9 4 2Maturitätsarbeit
9 5 5 5 9gesprengt.
619894676783
744944825537977472684710404753464620804
3