4. Messung nichtelektrischer Größen 4.1 Temperatur
Werbung
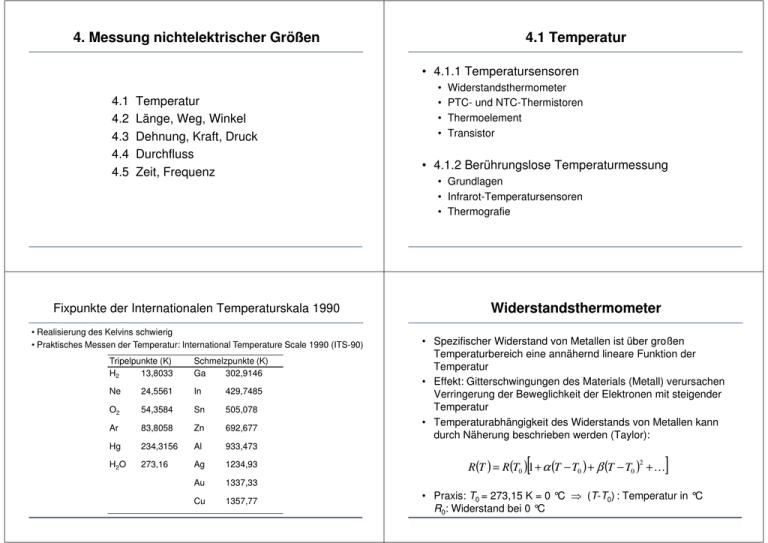
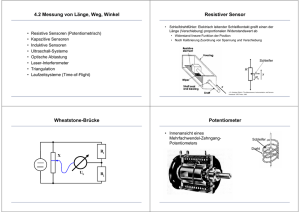
4. Messung nichtelektrischer Größen 4.1 Temperatur • 4.1.1 Temperatursensoren 4.1 4.2 4.3 4.4 4.5 Temperatur Länge, Weg, Winkel Dehnung, Kraft, Druck Durchfluss Zeit, Frequenz Fixpunkte der Internationalen Temperaturskala 1990 • Realisierung des Kelvins schwierig • Praktisches Messen der Temperatur: International Temperature Scale 1990 (ITS-90) Tripelpunkte (K) H2 13,8033 Schmelzpunkte (K) Ga 302,9146 Ne 24,5561 In 429,7485 O2 54,3584 Sn 505,078 Ar 83,8058 Zn 692,677 Hg 234,3156 Al 933,473 H 2O 273,16 Ag 1234,93 Au 1337,33 Cu 1357,77 • • • • Widerstandsthermometer PTC- und NTC-Thermistoren Thermoelement Transistor • 4.1.2 Berührungslose Temperaturmessung • Grundlagen • Infrarot-Temperatursensoren • Thermografie Widerstandsthermometer • Spezifischer Widerstand von Metallen ist über großen Temperaturbereich eine annähernd lineare Funktion der Temperatur • Effekt: Gitterschwingungen des Materials (Metall) verursachen Verringerung der Beweglichkeit der Elektronen mit steigender Temperatur • Temperaturabhängigkeit des Widerstands von Metallen kann durch Näherung beschrieben werden (Taylor): [ ] R(T ) = R(T0 ) 1 + α (T − T0 ) + β (T − T0 ) + K 2 • Praxis: T0 = 273,15 K = 0 °C ⇒ (T-T0) : Temperatur in °C R0: Widerstand bei 0 °C Widerstandsthermometer • Gebräuchliche Materialien für Widerstandsthermometer: Platin (Pt) und Nickel (Ni) • Um Widerstand zu messen, wird Spannung über stromdurchflossenem Widerstand gemessen: • Erwärmung ⇒ Messung mit kleinen Strömen (≈ 1 mA) • Optimal: Messung mit konstantem Strom Platin-Widerstandsthermometer • Temperaturbereich: -200 – 1000 °C • Hohe Genauigkeit: Platin-Widerstandsthermometer mit Unsicherheit von ± 0,1 mK möglich • Industriell eingesetzte Platin-Widerstandsthermometer: • Pt 100: R0 = 100 Ω , Pt 1000: R0 = 1000 Ω, • Einflussgrößen: Deformation und Verunreinigungen • Gehäuse beeinflusst Zeitverhalten: α = 3,90802×10-3 K-1 , β = -0,580195×10-6 K-2 (0 °C – 850 °C) • Zeitkonstanten im Bereich ms - min • α und β abhänging von Verunreinigungen des Materials Platin-Widerstandsthermometer Lineare Näherung • Quadratischer Term kann in vielen Fällen vernachlässigt werden (β ≈ α⋅10-3) • Lineare Näherung: R(T ) = R(T0 )[1 + α (T − T0 )] • mit α = 3,85×10-3 K-1 Näherung im Bereich 0-100 °C (DIN IEC 751) Lineare Näherung im Bereich 0 – 100 °C • Ursache für Abweichung von α zwischen linearer Näherung und quadratischer Näherung: Lineare Kennlinie nicht durch Taylor-Approximation berechnet sondern exakt gültig für 0 °C und 100 °C • Prinzip (übertriebene Darstellung, nicht Pt 100!): 1.6 R(T) (nicht Pt 100) R (T) / R0 1.4 1.2 1 0.8 IEC: International Electrotechnical Commission Lineare Näherung im Bereich 0 – 100 °C 20 0 20 40 60 80 Temperatur (°C) 100 120 Pt 100 Widerstandsthermometer • Großer Temperaturbereich, hohe Genauigkeit (± 0,1 K Standard) 250 Nickel Widerstandsthermometer • Temperaturbereich: -60 – 200 °C • α = 6,6×10-3 K-1 , β = 7,58×10-6 K-2 • Höhere Empfindlichkeit als Pt, größere Abweichung von linearer Näherung 400 Lineare Näherung Ni 300 R (Ω) R (Ω) 200 150 Pt 100 200 100 100 50 100 50 0 50 100 150 200 250 300 Temperatur T (°C) NTC: Heißleiter • Effekt: Leitfähigkeit von Halbleitern (Fermi-Dirac Statistik) und von keramischen Materialien ist eine Funktion der Temperatur • Nichtlineare Kennlinie 8 10 R (Ω) R(T ) ≈ Ae 1 10 • Linearisierung durch Widerstandsnetzwerk möglich • Material: Fe2O3, TiO2… 6 10 4 10 2 10 50 0 50 100 150 Temperatur T (°C) 200 250 PTC Thermistor: Kaltleiter • NTC: Negative temperature coefficient B T 0 100 5 4 • Ferroelektrische Keramiken: Permanente Polarisierung nimmt über Ferroelektrischer Curie-Temperatur ab ⇒ Starker Anstieg des spezifischen Widerstands • Anstieg des Widerstands an Korngrenzen, wo sich durch wegfallende Polarisation ladungsträgerverarmte Zonen bilden • Material: z.B. Bariumtitanat (BaTiO3) 4 4 4 0 20 0 20 40 60 80 100 120 140 Temperatur T (°C) EPCOS Thermoelement PTC • Seebeck-Effekt: Temperaturgradient in einem elektrisch leitenden Material verursacht Potentialdifferenz zwischen Regionen mit unterschiedlichen Temperaturen • Quantitative Beschreibung erfordert quantenmechanische Betrachtung • Kennlinie eines PTC • Niedrige Genauigkeit dU = σ (T )dT • Anwendung: Schalter, Sicherungen, Kurzschlusssicherung, Selbstregulierende Heizelemente • σ: absoluter Seebeck Koeffizient T2 U = ∫ σ (T )dT T1 U J. G. Webster (Editor): “The Measurement, Instrumentation, and Sensors Handbook” CRC Press, 1999. EPCOS Thermoelement • Vereinfachtes Modell: Besetzung von Energieniveaus in Festkörpern ist abhängig von der Temperatur ⇒ Temperaturgradient verursacht Gradienten in potenzieller Energie von Elektronen (und Löchern) • Effekt ist in allen Leitern vorhanden (keine Kontaktstellen benötigt) Thermoelement • Thermoelement Messobjekt Referenztemperatur (z.B. Eiswasser: 0 °C) B Tm Tr A • Aber: Zur Messung ist mindestens ein anderes Material notwendig ⇒ Thermoelement mit zwei Materialien • Ursache: bei Rückführung eines Materials zum Ort, an dem Spannung gemessen werden soll, tritt entgegengesetzter Temperaturgradient auf ⇒ Spannung verschwindet • Alle Leitungen und Kontakte tragen zur Spannung bei U A Ti • A, B: Materialien mit unterschiedlichen Seebeck-Koeffizienten Thermoelement Seebeck-Koeffizienten und Typbezeichnungen Material • Berechnung der Spannung: • Näherung: Seebeck-Koeffizienten konstant • Normung von Thermoelementen: − U = σ A (Tr − Ti ) + σ B (Tm − Tr ) + σ A (Ti − Tm ) B = σ A (Tr − Ti + Ti − Tm ) + σ B (Tm − Tr ) = σ A (Tr − Tm ) + σ B (Tm − Tr ) = (σ B − σ A )(Tm − Tr ) Tm Tr A U A Ti • Nichtlineare Näherung der Spannung von Thermoelementen gegeben in IEC 584-1 • Beispiel: Fe-CuNi : • [T] = °C U = 0,0394 mV mV ⋅ T + 3,1444 ⋅ 10 −5 2 ⋅ T 2 °C °C Name (Typ) Material B PtRh-PtRh (70/30, 94/6) K NiCr-Ni L, J Fe-CuNi R, S T, U PtRh-Pt Cu-CuNi • Positiv: Keine externe Energieversorgung notwendig (aktiver Sensor) Einfache Systeme möglich Niedrige Kosten Großer Messbereich (-270 °C – 2400 °C) • Negativ: • Nichtlineare Kennlinien • Niedrige Ausgangsspannungen (niedrige Empfindlichkeit) • Referenztemperatur benötigt (relative Temperaturmessung) 500 Antimon 47 Nickel-Chrom 25 Eisen 19 Kupfer 6.5 Gold 6.5 Silber 6.5 Rhodium 6.0 Tantal 4.5 Blei 4.0 Aluminium 3.5 Platin 0 Natrium -2.0 Kalium -9.0 Nickel -15 Konstantan (CuNi) -35 Bismut -72 Vergleich: Thermoelement und Widerstandsthermometer Eigenschaften von Thermoelementen • • • • Seebeck-Koeffizient (µV/K) bei 0 °C Tellur Widerstandsthermometer Thermoelement Bereich -270 – 1000 °C -270 – 2400 °C Typische Linearität (industrieller Sensor) ± 0,1 °C ± 1 °C LangzeitWiederholbarkeit (1 Jahr) besser als ± 0,5 °C > ± 1 °C Fehlerquellen Stromquelle, Selbsterwärmung Referenztemperatur, Leitungen Empfindlichkeit bis zu 5 mV/°C bis zu 50 µV/°C Schaumburg: Sensoren, Teubner, Stuttgart, 1992. Kennlinie: Transistor Transistor als Temperatursensor • Spannung über pn-Diode, durch die in Durchlassrichtung Strom fließt, ist abhängig von der Temperatur • Für konstanten Strom IF ist Spannung in guter Näherung lineare Funktion der Temperatur (in kleinem Temperaturbereich) • Gebräuchliche Schaltung: als Diode eingesetzter Transistor kT I U F = ln F e IS • • • • • k = Boltzmann-Konstante (1.38×10-23 J K-1) T = Temperatur (K) e = Elementarladung (1.6×10-19 C) IF = Strom IS = Sperrstrom • Messbereich: -40 °C – 150 °C • Empfindlichkeit (IC = 0.1 mA): ≈ -2 mV/K • Unterschiedliche Achsenabschnitte der Basis-EmitterSpannung (UBE) produktionsbedingt UBE = UF J. G. Webster (Editor): “The Measurement, Instrumentation, and Sensors Handbook” CRC Press, 1999. J. G. Webster (Editor): “The Measurement, Instrumentation, and Sensors Handbook” CRC Press, 1999. Linearität: Transistor • Linearität (MTS102) Linearisierung • Ursache für Nichtlinearität: Sperrstrom IS ist Funktion der Temperatur kT I U F = ln F e IS • Spannungsdifferenz bei zwei unterschiedlichen Strömen ist lineare Funktion der Temperatur J. G. Webster (Editor): “The Measurement, Instrumentation, and Sensors Handbook” CRC Press, 1999. J. G. Webster (Editor): “The Measurement, Instrumentation, and Sensors Handbook” CRC Press, 1999. Integrierte Schaltungen mit Transistoren als Temperatursensoren Linearisierung • Spannungsdifferenz bei zwei unterschiedlichen Strömen ist • nicht Abhängig von Is • lineare Funktion der Temperatur kT I F 1 U F1 = ln e I S U F1 − U F 2 kT I F 2 UF2 = ln e I S I kT I F 1 = − ln F 2 ln IS e I S kT = ln e I F1 IS IF2 IS • Signalverarbeitung (Linearisierung, Verstärkung, Digitalisierung) auf einem Chip möglich (Massenproduktion) • Integrierte Sensoren mit digitalem Ausgang verfügbar • Beispiel: LM 76 = kT ln I F 1 e I F2 • Eigenschaften von Transistoren als Temperatursensoren • Positiv: • Gute Linearität • Niedrige Kosten • Integrierte Sensoren mit digitalem Ausgangssignal verfügbar • Kann in integrierten Schaltungen eingesetzt werden • Negativ: • Eingeschränkter Temperaturbereich (National Semiconductor) LM76CHM-5: I2C serial bus interface Bereich: -10°C bis +45°C Unsicherheit: ± 1 °C Preis: ≈ 1 €