Kapitel 1 Nullstellen von P olynomgleichungen

x
x
x
a/2
2
Leider fehlt hier nun nicht nur ein Würfel der Kantenlänge 3 , sondern
auch noch drei quadratische Säulen der Höhe auf Grundflächen mit
Seitenlänge 3 . Wir können das Volumen des Würfels mit Seitenlänge
+ 3 also nicht einfach durch die bekannten Größen
ausdrücken,
sondern haben auch noch einen Term mit der Unbekannten .
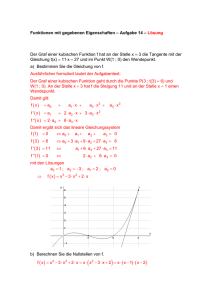
Die linke Zeichnung zeigt dieses Quadrat und darüber das Rechteck;
auf der rechten Seite ist die Hälfte des Rechtecks neben das Quadrat
gewandert, so daß abgesehen von dem kleinen Quadrat rechts oben
x
+
Wenn wir versuchen, für die Gleichungen 3 + 2 = ähnlich zu
argumentieren, müssen wir ins Dreidimensionale gehen und auf den
Würfel mit Kantenlänge eine quadratische Säule mit Basisquadrat
der Seitenlänge und Höhe stellen. Um sie so zu verteilen, daß wir
möglichst nahe an einen neuen Würfel kommen, müssen wir jeweils ein
Drittel davon auf drei der Seitenflächen des Würfels platzieren:
=
a/2
a
= geoWenn wir beispielsweise die quadratische Gleichung 2 +
metrisch interpretieren wollen, suchen wir nach einem Quadrat einer
unbekannten Seitenlänge derart, daß die Fläche des Quadrats zusammen mit der des Rechtecks mit Seiten und gleich ist.
.
2
4
Dieses Verfahren war zumindest grundsätzlich in allen frühen Hochkulturen bekannt; die ersten bekannten Hinweise darauf finden sich bereits
vor über vier Tausend Jahren bei den Babyloniern.
Um 830 legte der arabische Gelehrte MUHAMMAD IBN MUSA ABU
DSCHA’FAR AL-CHWARIZMI sein zweites Buch Al-Kitāb al-muchtasar
fi hisab al-dschabr wa-l-muqabala (Rechnen durch Ergänzung und
Ausgleich) vor; al-dschabr gab der Algebra ihren Namen und ALCHWARIZMI führte zum Wort Algorithmus. Das Buch befaßte sich mit systematischen Lösungsverfahren für lineare und quadratische Gleichungen, die auch geometrisch motiviert und veranschaulicht wurden.
§1: Quadratische Ergänzung
nun ein Quadrat mit Seitenlänge + 2 entstanden ist. Die Größe des
kleinen Quadrats ist bekannt: Seine Seitenlänge ist 2 . Wir suchen somit
eine Zahl
derart, daß das Quadrat mit Seitenlänge + 2 die Fläche
2
+ 4 hat; das Problem ist also zurückgeführt auf das Ziehen einer
Quadratwurzel:
Kapitel 1
Nullstellen von Polynomgleichungen
Kap. 1: Nullstellen von Polynomgleichungen
Computeralgebra WS 2008
1
+
+
1
+
0
= 0,
1
+
1
+
0
=0
2
+
2
+
:=
+
2
+
+
Wie wir bald sehen werden, ist das nicht immer wünschenswert; Zwischenergebnisse können in der Computeralgebra oft sehr umfangreich
sein und mehrere Bildschirmseiten in Anspruch nehmen. Falls die Ausgabe des Ergebnisses nicht erwünscht ist, muß der Befehl einfach mit
einem Doppelpunkt anstelle eines Semikolons abgeschlossen werden.
3
Um den quadratischen Term von
zu eliminieren, müssen wir das
Polynom in der neuen Variable = + 3 schreiben; dies leistet der
Substitutionsbefehl
2
Im Falle = 2 hat dieses Polynom die Form 2 + , wir können also seine
Nullstellen einfach durch Wurzelziehen ermitteln. Für
2 haben wir
immerhin einen Term weniger als in der allgemeinen Gleichung -ten
Grades und müssen sehen, ob uns das bei der Lösung helfen kann.
(
1
&'
1)
)
eingegeben werden. Maple quittiert diesen Befehl mit der Ausgabe
*
(
+
-
1
3
+,
%
*
2
2
1
0
.,
%
2)
+
+
$
*,
$
+
/
Wir kommen also auf ein Polynom -ten Grades in , das keinen Term
1
mit
hat.
(
2
01
2
1
1
$
+
2
1)
0
%
2
(
2
+
1
1
+
In Maple werden mathematische Ausdrücke, die nur Grundrechenarten
enthalten, in der üblichen mathematischen Notation eingegeben, allerdings darf das Multiplikationszeichen nie weggelassen werden. Für
die Exponentiation wird das Zeichen verwendet, für Zuweisungen .
Als Variablen können (unter anderem) alle mit einem Buchstaben beginnenden Folgen aus Buchstaben und Ziffern verwendet werden; abgeschlossen wird ein Befehl im allgemeinen mit einem Strichpunkt. Die
Definition eines Polynoms vom Grad drei kann somit in der Form
Computeralgebrasysteme sind Programme zum symbolischen Rechnen,
die genau für solche Zwecke entwickelt wurden – auch wenn ihre Fähigkeiten heute meist weit darüber hinausgehen. Hier soll beispielhaft das
Computeralgebrasystem Maple betrachtet werden; in anderen Systemen werden die Befehle zwar im allgemeinen etwas anders aussehen,
bezüglich der grundsätzlichen Fähigkeiten gibt es aber keine nennenswerten Unterschiede.
Die Elimination des zweithöchsten Terms läßt sich für Gleichungen
nicht allzu hohen Grades problemlos explizit durchführen, ist aber eine
eher unangenehme und ziemlich langweilige Rechnung. Gerade in der
Computeralgebra sollte man so etwas besser einem Computer überlassen.
&'
=
+
1
2
1
+
+
1
1
+
+
+
1
+
1
=
1
2
+
2
1
+
2
=
1
1
+
Geometrisch betrachtet wollen wir einen -dimensionalen Hyperwürfel
1
bekommen, dessen Seitenlänge +
sein sollte; rechnerisch bedeutet
1
dies, daß wir die neue Variable = +
betrachten und überall in
1
der Gleichung durch
ersetzen:
+
mit höchstem Koeffizienten eins.
1
+
nicht verschwindet. Falls wir
wobei wir natürlich voraussetzen, daß
diviüber einem Körper wie oder arbeiten, können wir durch
dieren und erhalten die neue Gleichung
1
+
§2: Polynome in Computeralgebrasystemen
Kap. 1: Nullstellen von Polynomgleichungen
Trotzdem ist diese Idee nützlich, sogar für Gleichungen höheren Grades.
Die allgemeine Gleichung -ten Grades hat die Form
–
#
!
"
< 1
)
9
+;:
78
6
/
4
*
'
45
3
&'
(
=
3
+
2
>
:=
Computeralgebra WS 2008
-A
@
?
(
4DH
6
B
*
< 1
3
B
(
-A
@
?
*
>
2
C
<
<
6G
:
F
E
7
6G
7
?
0
E
0D
C
I
I
I
L
!
I
I
F
4DH
I
< 1
7
< :
7
I :
6
F
E
?
6
J
(
0
E
0D
F
4DH
&'
:
K
L
!
7 :
G
G
G?
Somit haben wir ein Polynom der Form + + gefunden; mit dem
Befehl
oder
können wir und
noch isolieren, wobei für natürlich nur die zweite Form in Frage
kommt. Alternativ läßt sich auch isolieren, indem wir einfach auf
Null setzen:
F
3
M :
3
- :
3
/ :
3
3
+ =0
S
R
6G
%A
6G
:
3
+3
2
+3
2
+
3
S
S
R
S
R
R
L
R
S
R
!
S
R
L
3
+
3
+ ) + (3
+ )( + ) = 0 ,
!
<
A
:
<
(
R
+ ( + )+ = 0.
S
Dies können wir auch anders zusammenfassen als
3
+ führt auf die Bedingung
S
( + ) + ( + )+ =
Einsetzen von
=
Der Trick, der schließlich zum Erfolg führte, ist folgender: Wir schreiben
die Variable als Summe zweier neuer Variablen und und machen
dadurch das Problem auf den ersten Blick nur schwieriger. Andererseits
ist diese Summendarstellung natürlich alles andere als eindeutig; wir
können daher hoffen, daß es auch dann noch Lösungen gibt, wenn wir
an und zusätzliche Forderungen stellen und dadurch das Problem
vielleicht vereinfachen.
explizit zu lösen. Auch wenn die Griechen geometrische Konstruktionen
(jenseits von Zirkel und Lineal) kannten, mit denen sie Lösungen kubischer Gleichungen konstruieren konnten, sollte es noch bis ins 16. Jahrhundert dauern, bevor eine explizite Lösungsformel gefunden war – ein
Zeichen dafür, daß der Lösungsansatz nicht gerade offensichtlich ist.
+
Unser nächstes Ziel ist es, die Gleichung
2 3
+
27
< 1
Q
0
!
+
+
2
6
L
+
P
+
3
:=
§3: Kubische Gleichungen
2 3
27
Damit ist klar, wie es weitergeht:
+
Wenn wir einen Ausdruck als Polynom in dargestellt sehen wollen,
müssen wir den Befehl
eingeben; zum Sortieren der
. Für ein überTerme von nach Potenzen von dient
sichtliches Ergebnis sollten wir hier gleich beides anwenden. Da wir
dem letzten Ergebnis keinen Namen gegeben haben, müssen wir auch
noch eine neue Variable kennen lernen: bezeichnet in Maple stets das
Ergebnis der letzten Ausgabe; daneben gibt es noch
für die vorletzte
und
für die drittletzte.
L
:=
L
2 3
+
+
3
27
3
Das Ergebnis sieht ziemlich nach Kraut und Rüben aus, allerdings war
das auch nicht anders zu erwarten: Zwar betrachten wir als die Variable
dieses Polynoms und
als Parameter, aber das kann Maple nicht
wissen. So wie wir
und
eingegeben haben, sind
und
gleichberechtigte Variablen.
!
+
2
3
3
3
2
2
+
27
3
Wir können das Ergebnis für auch noch etwas sortierter darstellen:
:=
Kap. 1: Nullstellen von Polynomgleichungen
+
+
3
3
3
Einige ältere Computeralgebrasysteme wie beispielsweise REDUCE
hätten gleich ausmultipliziert; die meisten heute gebräuchlichen Systeme verzichten darauf, sofern es nicht explizit verlangt wird. Der Befehl
zum Ausmultiplizieren heißt
:
–
O
L
S
R
S
R
!
S
R
L
S
R
< 1
J
N :
6
/
7
6
4
7'
G?
0D
45
L
M
0D
(
@
&'
< 1
7
J :
G
G?
0D
&'
Computeralgebra WS 2008
T
S
R !
L
R
S
S
R
S
R !
S
R
R
S
L
S
R
W
Y
2
X
W
U
UV
U
W
Z
Z
Z
Y
Y
U
L
[
L
2
+
,
3) =
3
6
2
+ 11
6;
+6
2
+ 12 + 8
6
2
24
2
6
24 + 11 + 22
6( + 2) + 11( + 2)
6=
L
L
!
3
,
!
L
L
S
1) = ( + 1)(
1)
genau an den Stellen = 1 0 1 verschwindet, und da
hat die Ausgangsgleichung die Lösungen = 1 2 3.
2
= (
3
=
+ 2 ist,
wir müssen also zunächst die Gleichung 3
= 0 lösen. Hierzu
brauchen wir selbstverständlich keine Lösungstheorie kubischer Gleichungen: Ausklammern von und die dritte binomische Formel zeigen
sofort, daß
=
3
( + 2)
3
Falls wir das nicht wüßten, würden wir als erstes durch die Substitution
=
2 den quadratischen Term eliminieren. Einsetzen von = + 2
liefert
!
Somit kennen wir 3 und 3 . Für und selbst gibt es dann jeweils
drei Möglichkeiten, Allerdings führen nicht alle neun Kombinationen
dieser Möglichkeiten zu Lösungen, denn für eine Lösung muß ja die
1 3
Bedingung 3 =
erfüllt sein, nicht nur 3 3 = 27
.
2)(
3
!
3
1)(
2
2
3
wobei es auf die Reihenfolge natürlich nicht ankommt.
R
=
3
2
,
2
+
+
3
(
sie hat nach Konstruktion die drei Lösungen 1 2 und 3.
und
=
2
2
4 3
27
=
X
+
2
4
Y
+
Y
2
2
X
3
=
3
Betrachten wir dazu als einfaches Beispiel die Gleichung
In unserem Fall ist daher
+ = 0;
2
3
oder umgekehrt.
X
Y
W
4
U
2
U
W
und
Z
2
und also einfach als Lösungen
2
Y
+
=
Z
=
Z
( + ) +
X
falls wir und kennen, erhalten wir
einer quadratischen Gleichung:
W
W
)=
U
)(
R
(
und
R
Da selbst von den drei Kubikwurzeln einer reellen Zahl nur eine reell
ist, müssen wir zur Bestimmung aller drei Lösungen einer kubischen
Gleichung immer auch mit komplexen Zahlen rechnen, selbst wenn
sowohl Koeffizienten als auch Lösungen allesamt reell sind.
S
Haben zwei Zahlen
das Produkt und die Summe , so sind
die beiden Nullstellen der Gleichung
,
27
wir kennen also die Summe und das Produkt ihrer dritten Potenzen.
Damit kennen wir aber auch 3 und 3 :
R
=
R
3
!
3
R
und
^
=
L
3
2
+
2
+
L
+
3
wobei für nacheinander jede der drei Kubikwurzeln eingesetzt werden
muß. (Es spielt keine Rolle, welche der beiden Quadratwurzeln wir
nehmen, denn ersetzen wir die eine durch die andere, vertauschen wir
dadurch einfach und .)
=
L
3
R
mit
3
=
!
!
3
,
erfüllen erst recht die schwächere Bedingung
=
!
Zwei solche Zahlen
und 3
R
haben wir eine Lösung gefunden.
=
S
3
]
+
R
3
Dies läßt sich am besten dadurch gewährleisten, daß wir für irgendeine
3 setzen. Die
der drei Kubikwurzeln von 3 nehmen und dann =
3
drei Lösungen der kubischen Gleichung + + = 0 sind also
Kap. 1: Nullstellen von Polynomgleichungen
und natürlich verschwindet diese Summe insbesondere dann, wenn beide Summanden einzeln verschwinden. Falls es uns also gelingt, zwei
Zahlen
zu finden mit
–
\
S
R
S
R
R
S
!
R
S
_
L
=
^
R
S
R
S
S
R
R
S
a
`
b
b
`
a
a
b
a
b
`
R
a
b
a
R
S
b
(
?i
b
a
S
a
R
a
R
a
b
a
`
1
10 3
arctan
+
3
27
3
1
10 3
+
arctan
3
27
3
6
kG
E
kl
4
(
b
:=
< 1
I
7
a
@
a
b
a
S
@
kl
4
1
arctan
3
b
a
b
R
S
R
a
10 3
27
1
arctan
3
10 3
27
+
+
+ sin
1
7 3 cos
3
3
3
j
7 +6 = 0.
6
a
Etwas komplizierter wird es bei der Gleichung
<
= 1.
6
+
<
2(3 + 3 ) 1
3
= +
2
2
2
6
3 + ( 3)
6
= 6 in die
Dieses Ergebnis ist offensichtlich noch nicht in der bestmöglichen Weise
dargestellt; mit dem Kommando
können wir Maple dazu
überreden, sich etwas mehr Mühe zu geben:
<
=
6
2
1
1 13
7
9 3 21 6 cos
9
1
2
1
1
+ 7 3 9 3 21 6 sin
9
3
6
E
j
=
<
kG
und liefert so die Lösung
a
6
7
3
b
2
?i
-
1
=
3
3
-
0
a
=
b
0
<
j
schließlich führt auf
a
<
3
6
E
E
1
2
8
6
=
I
3
2
+,
< 1
1
2
f
1
3
¯=
3
3
N
b
=
9g
j
Die dritte Kubikwurzel
H4
1.
M
a
=
F
+
=
e
wir erhalten somit die Lösung
und erhalten unsere Eingabe unausgerechnet zurück. Mit dem Befehl
können wir Maple veranlassen, das Ergebnis – falls möglich – in
der Form + darzustellen:
1
3
<
1
3
;
+
2
6
X
2(3
3 )
=
2
3 + ( 3)2
(
1
2
=
=
3
3+ 3
a
=
6
3
Y
und
$
3
6
$
1
2
+
=
6
a
3
2
h
1
+
2
< 1
+
1
3
=
3
3
f
10
9
6
=
R
%
3+
e
Im ersten Fall ist
b
<
3
2
<
1
2
H4
¯=
M
6
und
F
9
3
2
R
1
+
2
=
9
b
Die beiden anderen Kubikwurzeln erhalten wir, indem wir die reelle
Kubikwurzel mit einer der beiden komplexen dritten Einheitswurzeln
multiplizieren, d.h. also mit
3+
b
73
10
3
3+
3 .
=
27
9
Was nun? Wenn wir einen Ansatz der Form = + machen, kommen
wir auf ein System von zwei kubischen Gleichungen in zwei Unbekannten, also ein schwierigeres Problem als unsere Ausgangsgleichung.
Wir können auch Maple nach dem Wert dieser Kubikwurzel fragen:
Die imaginäre Einheit wird dort als großes eingegeben und Wurzeln
(abgesehen von der auch als
darstellbaren Quadratwurzel) durch
Potenzen mit gebrochenem Exponenten; wir tippen also
3
^
=
1
3
a
für die rein imaginäre Kubikwurzel. Das zugehörige muß die Gleichung
= 31 erfüllen, also ist =
und wir erhalten als erste Lösung
= + = 0.
!
1
=
27
!
6
7 und
1
=
27
=
L
3
Da sie keinen 2 -Term hat, können wir gleich
Formel einsetzen und erhalten
Kap. 1: Nullstellen von Polynomgleichungen
Wenden wir trotzdem unsere Lösungsformel an: Bei dieser Gleichung
ist = 1 und = 0, also
Computeralgebra WS 2008
cd
–
b
&'
R
5
b
Computeralgebra WS 2008
c
c
Z
=
m
o
b
b
r
n
m Z
a
+ sin
r
3
.
p
3
o
cos
qm
m Z
Z
r
s
6
s
s
s
< 1
<
t
@
E
$
+
6
o
4
0D
o
(
@
?
r
B
-A
*
o
F
&'
1 1
3
+
2 2
2
:= 1 +
3
3
`
M
H4
9
.,
f
8
tD
(H
GE
< 1
6
R
$
6
+
GE
(
9
<
tD
$5
H
,
tD
$
H
6 5
0
E
(
e
G
-
?i
< 1
6 5
-
?i
+
$5
w
<,
tD
6
w
F
?i
(
H?
y
-
x5
A
0D
$
6 5
0
E
?i
10
3 ,
9
2 3
.
3
a
a
j
a
s
a
s
3
3
2
+ 9 + 13 = 0 .
Wenn wir eine reelle Kubikwurzel finden können, ist die Situation auch
nicht unbedingt viel besser. Betrachten wir etwa die Gleichung
Obwohl die drei Lösungen 1 2 und 3 unserer Gleichung allesamt
ganzzahlig sind, konnten wir dies also durch bloßes Einsetzen in unsere
Formel nicht erkennen und konnten insbesondere die Kubikwurzel nur
durch Erraten und Nachprüfen in einer einfachen Form darstellen.
1
e
3
a
2 7
7
+
:=
5
e
4
=
7
6
h1
$
a
3
=
7
=2
&'
1
+
f,
x5
A
0D
$
=
<
y
-
10
3 +
27
3
=
3
gefunden. Die beiden anderen sind nun (etwas langwierige) Routine,
können also beruhigt Maple überlassen werden:
S
9
.
H?
1
arctan
3
=
R
.
F
sin
R
a
9
H4
= 1, daß
v
b
R
tD
+ cos2
b
S
$
6
und daraus folgt dann über die Beziehung sin2
M
3
,
7
b
F
3
=
3 7
b
<
<
=
a
b
a
9
+
< 1
10
3 +
27
3
S
ist
b
6
+
1
arctan
3
a
h1
$
cos
a
b
<
Wie jedes numerische Ergebnis stimmt diese Zahl natürlich nur näherungsweise, und zumindest in diesem Fall ist die Hypothese, daß es sich
beim Realteil um eine durch Rundungsfehler verfälschte Eins handeln
kann, eine Überlegung wert. Falls dem so sein sollte, ist
. Das zugehörige
u
2 3
3
8
3 =
9
b
1 000000001 + 1 154700538
a
=1+
4
Trotzdem ist die obige Darstellung der Lösung nicht völlig nutzlos:
Sie gibt uns immerhin Formeln für den Real- und den Imaginärteil
der Lösung, und diese Formeln können wir numerisch auswerten. Der
, wobei das für floating point steht,
Maple-Befehl dafür heißt
d.h. also für Gleitkommaarithmetik.
b
2 3
a
Um = cos 3 zu berechnen, müssen wir also die kubische Gleichung
4 3 3 = cos lösen, was uns wiederum auf die Berechnung einer
Kubikwurzel führt usw.
=1
3 cos( )
a
7
7
7(3 2 3 )
=
= 2
=1
3
3 + 22 3
3+2 3
Damit ist die erste Lösung
also ist
1
3
3
R
2 3
3
a
4 cos( )
b
Leider gibt es keine einfache Formel, die Sinus und Kosinus von 3 durch
cos und sin ausdrückt. Aus den Additionstheoremen können wir uns
natürlich leicht Formeln für cos 3 und sin 3 verschaffen; wenn wir
das nicht selbst ausrechnen wollen, tut es Maple für uns:
3
n
3
,
p
und
Z
+ sin
a
cos
a
=
=1
c
1
2 7
2 3
3 7
=1
3
7
3
ist. Bislang war alles noch Spekulation; nun kommt die Probe:
und
Kap. 1: Nullstellen von Polynomgleichungen
Maple arbeitet hier also mit der Polarkoordinatendarstellung komplexer
Zahlen: Jede komplexe Zahl läßt sich darstellen als
–
j
a
c
!
10 +
L
3
10 +
= 2 und
2
a
108 =
3
= 10, also
a
100 + 8 =
3
10 + 6 3
[
[
[
R
[
10 + 6 3
3
.
a
q
!
R
R
6 5
kG
9
6
<
<
6
E
kl
4
< 1
+
f
%
+
F
|
$
M
(
H4
N,
f
6
8
&'
5
a
R
< 1
9 5
.
7
8
@
<
6
<
6
a
<
6
a
< 1
I
6
E
(
0
-
?i
6 3,
3)
3.
R
`
a
a
n
a
(3
p
a
=
(3
(3
(1 +
8 3
n
3)
a
b
`
a
[
a
3)
3)
16
3)
2
2
a
3)(2 +
3) (2 +
4 (1
3)
3)
3)
(3 +
3)
b
2(2
3)
a
(1
b
a
=
+ (3
p
=
(1
n
3)2
3)
=
3) + (3
2
3)
,
b
a
q
10 + 6 3
R
2,
`
a
(3
3
=
a
a
3)2
a
3)
2
a
R
Damit ist
4 (1
2
=
(1
1
b
3)
(1
1+ 3
=
2
2
¯=( 1+
3)
b
a
3
=( 1+
R
und
3+
a
a
p
10 + 6 3
a
a
3
b
ist. Aber warum ist
12 + 20 = 0
8
2+2 3
= 2.
2
Nachdem wir in einfacher Form ausgedrückt haben, lassen sich nun
auch die anderen beiden Lösungen berechnen:
a
3
a
a
( 2) + 6 ( 2) + 20 =
a
2 in unsere kubische Gleichung zeigt in der Tat,
a
=
2( 1
3)
( 1 + 3)( 1
a
b
Einsetzen von
daß
1+
R
=
a
3
10
a
1 999999986
Wenn wir das allerdings numerisch auswerten, drängt sich wieder die
Hypothese auf, daß hier tatsächlich etwas sehr viel einfacheres steht:
3
a
1+
=
3 3=
1
a
1
3
a
1 + 3 und
2
= 1+
1+ 3
3 3
=
a
3 3
( 10 + 6 3)
R
also ist tatsächlich
1
2
R
a
a
2
3
a
( 10 + 6 3)
R
3
R
3) =
1
:= ( 10 + 6 3)
a
( 1
=
1
3
R
Quadratische Ergänzung macht daraus ( +1)2 = 3, also ist
Die dritte Potenz davon ist
10 + 6 3
2
a
Damit haben wir im Prinzip eine Lösung gefunden, die auch Maple nicht
weiter vereinfachen kann:
3
3
=
Im vorliegenden Fall, wo die numerische Berechnung eine Vermutung
nahelegt, können wir wieder versuchen, diese zu beweisen: Aus der
vermuteten Gleichung
2
2
= 2 folgt
2= 2 .
Wie die Erfahrung der Computeralgebra zeigt, kann es extrem schwierig
sein, auch nur zu entscheiden, ob zwei Wurzelausdrücke gleich sind;
direkte allgemeine Verfahren dazu gibt es nicht. Unsere Formel gibt uns
daher zwar immer drei Wurzelausdrücke, die Lösungen der gegebenen
Gleichung sind, aber diese können für Zahlen stehen, die sich auch sehr
viel einfacher ausdrücken lassen.
und wie, vor allem, kann man das der linken Seite ansehen?
R
1
a
=
Da 108 größer ist als ( 10)2 = 100, gibt es eine positive reelle Wurzel;
wir rechnen zunächst mit dieser und erhalten als erste Lösung
3
+ 2 + 1) + 9 + 9 + 13
a
=
z
= 20. Damit ist
+ 6 + 20 = 0
{
= 6 und
=
2
3
3(
mit
+3 +1
2
+3
3( + 1) + 9( + 1) + 13
2
3
3
=
+ 1 und erhalten die neue Gleichung
Kap. 1: Nullstellen von Polynomgleichungen
c
( + 1)
=
Computeralgebra WS 2008
Hier setzen wir
–
#
2
=
c
`
R
=
2
=1
¯
b
3.
3)
a
3) + (3 +
2
b
= 1+3 .
R
`
`
R
`
R
}
=0
X
L
!
Z
Z
!
X
Z
!
Z
!
L
Z
Z
Z
Z
R
R
Z
R
Z
R
+ ),
~
Z
Z
Y
R
€
Z

~
Z
Y
R
Z
2
~
Z
Y
u
Z
+4
2
+8
+
2
4
= 0.
2
+
2
0)
= (2
0
)
2
+
2
0
.
Es wäre nicht schwer, mit Hilfe der Lösungsformel für kubische Gleichungen, eine explizite Formel für die vier Lösungen hinzuschreiben;
sie ist allerdings erstens deutlich länger und zweitens für die praktische
Berechnung reeller Nullstellen mindestens genauso problematisch wie
die für kubische Gleichungen.
rechts das Quadrat eines linearen Polynoms in , das wir – da wir
alle Koeffizienten kennen – problemlos hinschreiben können. Dies führt
dann nach Wurzelziehen zu zwei quadratischen Gleichungen für , deren
Wurzeln die Nullstellen der biquadratischen Gleichung sind.
(
Nach der (mehr oder weniger) erfolgreichen Auflösung der kubischen
und biquadratischen Gleichungen in der ersten Hälfte des sechzehnten
R
Natürlich ist die rechte Seite (2
) 2
+ 2
im allgemeinen
kein Quadrat eines linearen Polynoms in ; wir können aber hoffen, daß
=0
Z
§5: Gleichungen höheren Grades
+ )+
R
lösen, um die Lösungen der biquadratischen Gleichung zu finden.
(
wir müssen also nur die beiden quadratischen Gleichungen
(
Y
=
+
L
2
~
2
L
Z
+ )
2
Z
+ ) =(
R
R
2
X
X
(
s
Z
+ steht, ist
L
Z
Falls rechts das Quadrat eines linearen Polynoms
Z
.
R
2
R
+
R
2
!
!
)
X
= (2
s
Z
2
‚
Dies ist eine kubische Gleichung für , die wir mit der Methode aus
dem vorigen Abschnitt lösen können. Ist 0 eine der Lösungen, so steht
in der Gleichung
3
R
R
L
+

R
2
8
!
Z
+2
R
)=
R
4
X
R
2
R
R
X
+ ) =
!
L
2
Z
(
s
2
L
!
Wir nehmen also an, wir hätten eine Lösung dieser Gleichung und
betrachten dazu für eine zunächst noch beliebige Zahl die Zahl 2 + .
2
, also
Da 4 + 2 + + verschwindet, ist 4 =

)(
X
4(2

2
Z
X
Zu deren Lösung benutzen wir einen anderen Trick als im kubischen
Fall: Wir versuchen, die Quadrate der Nullstellen durch eine geeignete
Verschiebung zu Lösungen einer quadratischen Gleichung zu machen,
die wir dann mit der bekannten Lösungsformel auflösen können.
+ = 0.
s
+
‚
2
s
+
2
s
4
s
= + 4 ; dies führt auf eine Gleichung der Form
+
durch die Substitution
+
=
.
2
4 2
Die Ausgangsgleichung ist genau dann das Quadrat eines linearen Polynoms, wenn beide Lösungen übereinstimmen, wenn also der Ausdruck
unter der Wurzel verschwindet. Bringen wir diesen auf den Hauptnen= 0. In unserem Fall ist
ner, kommen wir auf die Bedingung 2 4
= (2
), =
und = 2
; wir erhalten also die Bedingung
Z
2
‚
+
s
=0
Z
€
3
+
Z
+
s


+
‚
4
Z
2
2
Ein quadratisches Polynom
+
+ ist genau dann Quadrat eines linearen, wenn die beiden Nullstellen der quadratischen Gleichung
2
+ + = 0 übereinstimmen. Diese Nullstellen können wir einfach
berechnen:

Z
‚
Auch biquadratische Gleichungen lassen sich auflösen: Hier eliminiert
man den kubischen Term von
a
¯
(1 +
‚

§4: Biquadratische Gleichungen
=
+
R
3
a
3)
a
3) + (3
2
b

Entsprechend folgt
(1
b
=
es zumindest für gewisse spezielle Werte der bislang noch willkürlichen
Konstante eines ist.
Kap. 1: Nullstellen von Polynomgleichungen
c
2
Computeralgebra WS 2008
also
–
O
R
!
X
R
Z
L
Z
Z
T
…
„
c
ƒ
„
ƒ
…
‡
o
o
†
In einem Großteil dieser Vorlesung wird es um Methoden gehen, wie
man trotz des Fehlens brauchbarer Lösungsformeln Aussagen über die
§6: Der Wurzelsatz von Viète
Der ABELsche Satz besagt selbstverständlich nicht, daß Gleichungen
höheren als vierten Grades unlösbar seien; er sagt nur, daß es im allgemeinen nicht möglich ist, die Lösungen durch Wurzelausdrücke in
den Koeffizienten darzustellen: Für eine allgemeine Lösungsformel muß
man also außer Wurzeln und Grundrechenarten noch weitere Funktionen
zulassen. Beispielsweise fanden sowohl HERMITE als auch KRONECKER
1858 Lösungsformeln für Gleichungen fünften Grades mit sogenannten
elliptischen Modulfunktionen; 1870 löste JORDAN damit Gleichungen
beliebigen Grades.
EMIL ARTIN: Galoissche Theorie, 1959 (Neuauflage 2004 bei Deutsch)
Der norwegische Mathematiker NILS HENRIK ABEL
(1802–1829) ist trotz seinen frühen Todes (an Tuberkulose) Initiator vieler Entwicklungen der Mathematik des
neunzehnten Jahrhunderts; Begriffe wie abelsche Gruppen, abelsche Integrale, abelsche Funktionen, abelsche
Varietäten, die auch in der heutigen Mathematik noch
allgegenwärtig sind, verdeutlichen seinen Einfluß. Zu
seinem 200. Geburtstag stiftete die norwegische Regierung einen ABEL-Preises für Mathematik mit gleicher
Ausstattung und Vergabebedingungen wie die Nobelpreise; erster Preisträger war 2003 JEAN-PIERRE SERRE
( 1926) vom Collège de France für seine Arbeiten über
algebraische Geometrie, Topologie und Zahlentheorie.
Die Grundidee seines Beweises liegt in der Betrachtung von Symmetrien
innerhalb der Lösungsmenge: Man betrachtet die Menge aller Permutationen der Nullstellenmenge, die durch Abbildungen :
erreicht
werden können, wobei sowohl mit der Addition als auch der Multiplikation verträglich sein muß. ABEL zeigt, daß diese Permutationen für
allgemeine Gleichungen vom Grad größer vier eine (in heutiger Terminologie) nichtauflösbare Gruppe bilden und daß es aus diesem Grund
keine Lösungsformel geben kann, in der nur Grundrechenarten und Wurzeln vorkommen. Der Beweis ist so umfangreich, daß er (zusammen mit
den dafür notwendigen Definitionen und Sätzen) typischerweise den
größten Teil der Vorlesung Algebra I einnimmt; über Einzelheiten kann
daher hier nichts weiter gesagt werden. Interessenten finden ihn in fast
jedem Algebralehrbuch im Kapitel über GALOIS-Theorie. Ein kurzes,
gut lesbares Buch, das sich ganz darauf konzentriert, ist etwa
Die Lösung allgemeiner kubischer Gleichungen geht
auf den Mathematiker, Arzt und Naturforscher GIROLAMO CARDANO (1501–1576, unteres Bild) zurück, dem
TARTAGLIA nach langem Drängen und unter dem Siegel der Verschwiegenheit seine Methode mitgeteilt hatte. LODOVICO FERRARI (1522–1565) kam 14-jährig als
Diener zu CARDANO; als dieser merkte, daß FERRARI
schreiben konnte, machte er ihn zu seinem Sekretär.
1540 fand FERRARI die Lösungsmethode für biquadratische Gleichungen; 1545 veröffentlichte CARDANO in
seinem Buch Ars magna die Lösungsmethoden für kubische und biquadratische Gleichungen.
nächsten Fall, der Gleichung fünften Grades. Hier gab es jedoch über 250
Jahre lang keinerlei Fortschritt, bis zu Beginn des neunzehnten Jahrhunderts ABEL glaubte, eine Lösung gefunden zu haben. Er entdeckte dann
aber recht schnell seinen Fehler und bewies stattdessen 1824, daß es
unmöglich ist, die Lösungen einer allgemeinen Gleichung fünften (oder
höheren) Grades durch Grundrechenarten und Wurzeln auszudrücken.
Kap. 1: Nullstellen von Polynomgleichungen
c
Die erste Lösung einer kubischen Gleichung geht wohl
aus SCIPIONE DEL FERRO (1465–1526) zurück, der von
1496 bis zu seinem Tod an der Universität Bologna lehrte. 1515 fand er eine Methode, um die Nullstellen von
3+
= für positive Werte von und zu bestimmen
(Negative Zahlen waren damals in Europa noch nicht im
Gebrauch). Er veröffentlichte diese jedoch nie, so daß
NICCOLO FONTANA (1499–1557, oberes Bild), genannt
TARTAGLIA (der Stotterer), dieselbe Methode 1535 noch
einmal entdeckte und gleichzeitig auch noch eine Modifikation, um einen leicht verschiedenen Typ kubischer
Gleichungen zu lösen. TARTAGLIA war mathematischer
Autodidakt, war aber schnell als Fachmann anerkannt
und konnte seinen Lebensunterhalt als Mathematiklehrer in Verona und Venedig verdienen.
Computeralgebra WS 2008
Jahrhunderts beschäftigten sich natürlich viele Mathematiker mit dem
–
\
Computeralgebra WS 2008
_
c
C
+
1
+
2
2
+
+
2
2
+
1
+
0
Z
,
ˆ
.
Z Z
‰
Z‹
Z

‰
Z‹
‹‰ Š
ˆ
Z
Š
‹‰ Š
ΠZ
1
Z Z Z Ž
X
Z
C
Z Z
‰

L
L
L
4
!
27
3
=
3
[
^
R
2
+
3+
9
=
3
2
=
2
3
a
2
3
2=
`
!
bzw.
4.
3
`
R
¯ anstelle
2
a
R
R
Für die zweite und dritte Lösung müssen wir mit
3
a
2
3
3
a
=
8=
1
für die reelle Wurzel; die erste Lösung ist also


2

+
3

a
=
a
+
+ = 0 besagt er einfach, daß
und das Produkt gleich ist. Das
a
Für eine quadratische Gleichung
die Summe der Lösungen gleich
!
2

Man beachte, daß dieses Einsetzen unbedingt notwendig ist: Bei der
Gleichung ( ) = 3
6 + 6 = 0 hätten wir genauso vorgehen
können und wären auf dieselben drei Kandidaten gekommen, aber
(1) = 1 (2) = 2 und ( 3) = 3. Hier führt aber die Lösungsformel aus 3 relativ schnell ans Ziel: Einsetzen der Parameter = 6
und = 6 in die Lösungsformel führt zunächst auf
FRANÇOIS VIÈTE (1540–1603) studierte Jura an der
Universität Poitiers, danach arbeitete er als Hauslehrer.
1573, ein Jahr nach dem Massaker an den Hugenotten,
berief ihn CHARLES IX (obwohl VIÈTE Hugenotte war)
in die Regierung der Bretagne; unter HENRI III wurde er
geheimer Staatsrat. 1584 wurde er auf Druck der katholischen Liga vom Hofe verbannt und beschäftigte sich
fünf Jahre lang nur mit Mathematik. Unter HENRI IV arbeitete er wieder am Hof und knackte u.a. verschlüsselte
Botschaften an den spanischen König PHILIP II. In seinem Buch In artem analyticam isagoge rechnete er als
erster systematisch mit symbolischen Größen.
= ( 1)
0
..
.
..
.
Bei der Gleichung ( ) = 3 7 + 6 = 0 etwa, die uns in 3 so viele
Schwierigkeiten machte, ist das Produkt aller Nullstellen gleich 6;
falls sie alle ganzzahlig sind, kommen also nur 1 2 3 und 6 in
Frage. Aus diesen acht Zahlen müssen wir drei (nicht notwendigerweise
verschiedene) auswählen mit Produkt 6 und Summe null. Das geht
offensichtlich nur mit 1 2 und 3, und Einsetzen zeigt, daß dies auch
tatsächlich Nullstellen sind.
=
Z
=
)
3
Z
2
Allgemein ist
bis aufs Vorzeichen gleich der Summe alle Produkte
aus Werten mit verschiedenem Index. Diese Summen bezeichnet
man als die elementarsymmetrischen Funktionen in 1
und die
obigen Gleichungen als den Wurzelsatz von VIÈTE.
C
+
Z
+
X
1
X
=
X
1
Falls wir aus irgendeinem Grund erwarten, daß alle Nullstellen ganzzahlig sind, folgt aus der Tatsache, daß ihr Produkt gleich ( 1) 0 ist,
daß sie allesamt Teiler von 0 sein müssen. Außerdem ist ihre Summe
gleich
1.
Diese Summen, die sogenannten elementarsymmetrischen Funktionen,
sind für -Werte im mittleren Bereich recht umfangreich, die beiden
Fälle = 0 und =
1 können aber gelegentlich ganz nützlich sein,
um Lösungen zu erraten:
(
.
mit (nicht notwendigerweise verschiedenen) Nullstellen 1
)(
)
Dann ist auch ( ) = (
(
).
Ausmultiplizie1
2
ren und Koeffizientenvergleich liefert uns die Gleichungen
( )=
1
Angenommen, wir haben ein Polynom
hatten wir bereits in bei der Lösung kubischer Gleichungen ausgenutzt,
um zwei Zahlen mit vorgegebenen Werten für Summe und Produkt zu
berechnen.
Kap. 1: Nullstellen von Polynomgleichungen
Nullstellen von Polynomgleichungen höheren Grades machen kann. Die
folgende Methode führt nur in speziellen Fällen, dann aber mit sehr
geringem Aufwand zu Nullstellen:
–
d
R
L
L
!
!
c
3
`
a
`
`
a
3
2
b
3
a
a
4
1
2
3 und ¯ =
1
2
4 ,
‘
1
2
3
2
und
3 auf die
b
b
u
a
b
a
p
a
n
b
a
a
C
+ 14
3
52
2
14 + 51
5
318
C
15
5400
3
10176
2
+ 27648 + 32768
‰
1
2
4
8
16
32
schließlich ist 0 = 32768 = 2 ; hier wissen wir also nur, daß – sofern
alle Nullstellen ganzzahlig sind – jede Nullstelle die Form 2 haben
muß, wobei die Summe aller Exponenten gleich 15 sein muß und die
Anzahl der negativen Vorzeichen gerade. Einsetzen zeigt, daß
+ 27
6
( )=
Beim Polynom
4
mit 0 = 51 = 3 17. Da das Produkt aller Nullstellen diesen Wert haben
muß, kommen – falls alle Nullstellen ganzzahlig sind – für diese nur
die Werte 1 3 17 und 51 in Frage. Wäre eine der Nullstellen
51, müßten alle anderen den Betrag eins haben und die Summe könnte nicht gleich 14 sein. Daher muß eine Nullstelle Betrag drei und
eine Betrag 17 haben, die beiden anderen Betrag eins. Produkt 51 und
Summe 14 erzwingt dabei offensichtlich, daß sowohl +1 als auch 1
Nullstellen sind, außerdem 17 und +3. Einsetzen zeigt, daß alle vier
auch tatsächlich Nullstellen sind.
( )=
4
Betrachten wir als nächstes Beispiel das Polynom
=
3 3 2 3 4
2+33 4
2
2
führt. Natürlich erfüllen auch diese Zahlen den Satz von VIÈTE, jedoch
nützt uns dieser nichts, um sie zu erraten.
3
a
1
2
`
2
a
a
3
3
=
`
2 3
`
a
1
2
a
+
`
`
2¯
4¯
`
1
2
3
3
2
a
=
2
`
3
3
3
a
was nach Einsetzen von =
beiden komplexen Lösungen
R
a
2
a
=
3
a
2
2
=
2
2
=
2¯
Man beachte, daß diese Vorgehensweise nur funktioniert, wenn das
Polynom höchsten Koeffizienten eins hat; andernfalls ist das Produkt
der Nullstellen gleich dem Quotienten aus konstantem Koeffizienten
und führendem Koeffizienten mal ( 1)Grad .
die Nullstellen sind.
3
Kap. 1: Nullstellen von Polynomgleichungen
arbeiten und erhalten
Computeralgebra WS 2008
von
–