Serie 4 - Folgen und Reihen - D-MATH

Analysis D-BAUG
Dr. Meike Akveld
HS 2015
Serie 4 - Folgen und Reihen
1. Untersuchen Sie die nachstehenden Zahlenfolgen. Sind sie beschränkt? Sind sie monoton? Konvergieren sie, und falls ja, wie lautet ihr Grenzwert?
a) an = cos πn
3
b) an =
c) an =
1
+ n22 + n32
n2
3n4 −5n2 +2
7n4 −4n3
+ ··· +
n−1
n2
+
n
n2
d) a1 = 0, a2 = 1, an = 12 (an−1 + an−2 ) für n ≥ 3
√
√
e) an = n + 1 − n
p
f) an = (n + 1)n − n
Lösung
a) Offensichtlich ist {an } nach unten durch −1 und nach oben durch 1 beschränkt. Die
ersten zwei Folgenglieder sind
a1 = 21
und
a2 = − 12 .
Da cos bekanntlich 2π-periodisch ist, gilt für alle n ∈ N:
an+6 = an .
Deshalb kann die Folge nur monoton sein oder konvergieren, wenn sie konstant ist. Das
ist sie aber nicht. Also ist sie nicht monoton und konvergiert auch nicht.
b) Es gilt
1
2
3
n−1
n
1
1 n(n + 1)
1
1
+ 2 + 2 + ··· +
+ 2 = 2 (1 + · · · + n) = 2
= +
.
2
2
n
n
n
n
n
n
n
2
2 2n
1
Die Folge 2n
ist beschränkt (durch 12 von oben und 0 von unten), monoton fallend
und konvergiert gegen 0. Daher ist {an } ebenfalls beschränkt, monoton fallend und
konvergiert gegen 12 .
an =
c) Wir rechnen wie üblich
an =
3 − 5n−2 + 2n−4
3n4 − 5n2 + 2 n−4
·
=
7n4 − 4n3
n−4
7 − 4n−1
und da der Zähler gegen 3 und der Nenner gegen 7 konvergiert, konvergiert {an } gegen
3
7 . Insbesondere ist die Folge beschränkt. Monoton ist sie wegen
a1 = 0 <
3
200
<
= a3
7
459
jedoch nicht. Wir haben a1 < a3 und wäre sie monoton steigend, so würde auch
a3 ≤ limn→∞ an gelten.
1
d) Wir rechnen
1
1
(an+1 + an ) − an+1 = − (an+1 − an )
2
2
2
n
n
1
1
1
=
−
(an − an−1 ) = · · · = −
(a2 − a1 ) = −
.
2
2
2
an+2 − an+1 =
Daher gilt
an = a1 +
n−2
X
n−2
X
k=0
k=0
(ak+2 − ak+1 ) =
1
−
2
k
.
Das ist die Partialsummenfolge einer geometrischen Reihe mit Faktor q = − 12 und konvergiert bekanntlich. Daher ist {an } beschränkt. Offensichtlich ist sie nicht monoton,
denn a3 = 21 und somit a1 < a2 > a3 . Der Grenzwert ist nach der Summenformel für
1
die geometrische Reihe 1−(−1/2)
= 32 .
e) Wir rechnen
an =
=
√
√
√
√
n+1+ n
√
n + 1 − n = ( n + 1 − n)
√
n+1+ n
1
n+1−n
√
√ =√
√ .
n+1+ n
n+1+ n
√
√
Die Folge ist offensichtlich monoton fallend, konvergiert gegen 0 und ist daher auch
beschränkt.
f) Wegen
an =
=
p
p
p(n + 1)n + n
(n + 1)n − n =
(n + 1)n − n p
(n + 1)n + n
(n + 1)n − n2
n
1
p
=p
=q
(n + 1)n + n
(n + 1)n + n
1 + n1 + 1
ist die Folge monoton wachsend und konvergiert gegen 12 , daher ist sie auch beschränkt.
2. a) Sei an = a1 + (n − 1)d mit a1 ∈ R eine arithmetischeP
Folge reeller Zahlen. Finden
Sie eine explizite Formel für die n-te Partialsumme ni=1 ai einer arithmetischen
Reihe.
b) Sei an = a1 q n−1 mit a1 ∈ R eine geometrische Folge reeller Zahlen mit |q| < 1.
Zeigen Sie: {an } konvergiert gegen 0.
Lösung
2
a) Wir rechnen
n
X
n
X
ai =
i=1
i=1
(a1 + (i − 1)d) =
= na1 + d
n−1
X
n
X
a1 + d
i=1
i = na1 + d
i=0
n
X
i=1
(i − 1)
(n − 1)n
2
2a1 + d(n − 1)
n(a1 + an )
= n
=
.
2
2
b) Sei ε > 0. Wir wollen zeigen:
∃N (ε) ∈ N ∀n > N (ε) : |an | ≤ ε.
Sei N (ε) eine natürliche Zahl mit
N (ε) ≥ log|q| (ε|q|/|a1 |).
Wegen |q| < 1 und n > N (ε) gilt
|q|n < |q|N (ε) .
Daher gilt für alle natürlichen Zahlen n > N (ε), dass
|an | = |a1 ||q n−1 | =
|a1 ||q|n
|a1 ||q|log|q| (ε|q|/|a1 |)
|a1 | ε|q|
<
=
=ε
|q|
|q|
|q| |a1 |
und wir sind fertig.
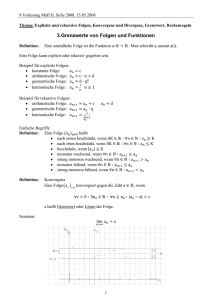
3. (Die Eulersche Zahl) Wir definieren zwei Folgen {an } und {bn } durch
1 n
an := 1 +
n
und
1 −n
bn := 1 −
.
n
bn = (1 − n1 )−n
b
b
e
b
b
bc
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
|
|
an = (1 + n1 )n
|
|
|
|
|
|
|
|
Ziel dieser Aufgabe ist zu zeigen, dass diese beiden Folgen gegen denselben Grenzwert
konvergieren. Dieser wird in der Vorlesung e, die Eulersche Zahl, genannt werden.
3
a) Zeigen Sie
bn+1 = an
1
1+
n
.
b) Zeigen Sie mit der Ungleichung von Bernoulli (siehe Serie 2, Aufgabe 1), dass
1
an
≥1−
bn
n
und folgern Sie, dass die Folge {an } monoton wächst.
c) Zeigen Sie auf ähnliche Weise, dass {bn } monoton fällt.
d) Folgern Sie, dass
lim an = lim bn .
n→∞
n→∞
Lösung
a) Bemerke zuerst, dass wir die Folgen alternativ auch folgendermassen darstellen können
n+1 n
an =
n
und
bn =
n−1
n
−n
=
n
n−1
n
.
Wir rechnen
n + 1 n+1
=
n
n+1
1
= an
= an 1 +
.
n
n
bn+1
b) Zu beweisen ist, dass
Es gilt
1 n
1 n
1
1+
1−
≥1− .
n
n
n
1 n
1 n
1
1 n
1 n
1+
1−
=
1+
1−
= 1− 2
.
n
n
n
n
n
Auf die rechte Seite wenden wir Bernoulli an:
1 n
1
1
1− 2
≥1−n 2 =1− .
n
n
n
Daher gilt mit a)
1
1
1
an ≥ 1 −
bn = 1 −
1+
an−1
n
n
n−1
n−1 n
=
an−1 = an−1 .
n n−1
4
c) Zuerst wollen wir folgende Ungleichung zeigen:
bn
1
>1+ .
an
n
Wieder wenden wir Bernoulli an:
n n n
n
n
n2
bn
=
=
an
n−1
n+1
n2 − 1
n
1
1
1
1
= 1+ 2
≥1+n 2
>1+n 2 =1+ .
n −1
n −1
n
n
Die Monotonie erhalten wir dann wieder mit a) durch
1
an = bn+1 .
bn > 1 +
n
d) Die Folgen {an } und {bn } sind beide monoton. Weiter gilt wegen a) für jedes n ∈ N:
an < bn+1 < b1
und
bn > an−1 > a1 ,
daher sind die Folgen {an } und {bn } nach oben beziehungsweise unten beschränkt.
Somit konvergieren sie. Um den Grenzwert zu berechnen, beobachten wir, dass
lim 1 +
n→∞
1
=1
n
und daher gilt wegen a)
lim bn =
n→∞
lim bn+1
1
= lim an 1 +
n→∞
n
1
= lim an · lim 1 +
n→∞
n→∞
n
= lim an · 1
n→∞
n→∞
=
lim an .
n→∞
4. Untersuchen Sie die Konvergenz folgender Reihen:
a)
b)
c)
P∞
√
3k+5
3k
P∞ 1+2k
k=1 k+3k
P∞ k!
k=1 kk
k=1
5
√
k−√ k
k=1 (k+ k)2
d)
P∞
e)
P∞
k=1
ln (k−1 +7) cos (kπ)
√
k+π
Lösung
a) Hier können wir das Quotientenkriterium verwenden.
p
3(k + 1) + 5
ak+1
3k
√
·
=
ak
3k+1
3k + 5
s
r
3 + k8 k→∞ 1
3k + 8
1
1
= ·
−→ < 1
= ·
3
3k + 5
3
3
3 + k5
Es folgt also, dass die Reihe konvergiert.
b) Wir schätzen die Folgenglieder ab.
1 + 2 k 2k + 2 k
2 · 2k
≤
|ak | = =
k + 3k 3k
3k
k
2
= 2
.
3
Wir haben also die geometrische Reihe mit a = 2 und q = 23 < 1 als konvergente
Majorante gefunden. Daraus folgt, dass die gegebene Reihe konvergiert.
c) Die Reihe konvergiert. Nachweis mittels Quotientenkriterium:
(k+1)!
(k+1)(k+1)
k!
kk
kk
(k + 1)k!k k
(k + 1)(k + 1)k k!
k
k
=
=
k+1
(k + 1)k
(k+1) −1
1
1
k→∞ −1
=
1−
· 1−
−→ e < 1.
k+1
k+1
|
{z
} |
{z
}
ak+1 ak =
=
k→∞ −1
−→ e
k→∞
−→ 1
Beachte, dass der erste Faktor der letzten Zeile mit (bk+1 )−1 aus Aufgabe 3 übereinstimmt.
d) Sei ak :=
√
k−√ k
.
(k+ k)2
Nun ist
√ √
k 1 − 1/ k
1
1 − 1/ k
√
√
ak =
;
= ·
k 1 + 2/ k + 1/k
k 2 1 + 2/ k + 1/k
|
{z
}
=:bk
6
der zweite Faktor bk strebt gegen 1, es gibt also ein K mit bk ≥ 12 , ∀k ≥ K. Somit
∞
X
k=1
ak ≥
K
X
k=1
∞
1 X 1
.
ak +
2
k
k=K+1
Wir haben also eine divergente Minorante erhalten. Daraus folgt, dass die gegebene
Reihe divergiert.
e) Sei
ln (k−1 +7) cos (kπ)
√
k+π
= (−1)k
ln (k−1 +7)
√
k+π
=: (−1)k ak .
Weil x 7→ ln(x) monoton wachsend ist, ist die Funktion x 7→ ln( x1 +7) monoton fallend.
√
Ausserdem ist der Nenner die monoton wachsende Funktion x 7→ x + π. Wir können
−1 +7)
√
also folgern, dass x 7→ ln (x
monoton fallend ist. Deswegen ist die Folge {ak }k
x+π
monoton fallend.
Weil
ln 8 k→∞
ln (k −1 + 7)
≤√
−→ 0,
0 ≤ ak = √
k+π
k+π
konvergiert die Folge {ak }k gegen 0. Also handelt es sich um eine monoton fallende
Nullfolge und die dazugehörende alternierende Reihe konvergiert.
7