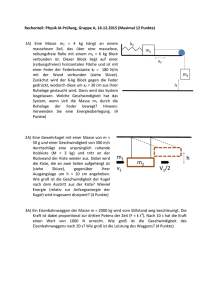
Schwingungslehre-Prüfungsaufgaben - gilligan

Prüfungsaufgaben
Schwingungslehre
Günther Kurz
Idee: Jürgen Gilg
Gestaltung: Simon Singer
Anregungen und Kommentare willkommen
[email protected]
Schwingungslehre – Prüfungsaufgabe 01
Ein Körper (Masse m = 50 g ) ist an einer idealen Feder befestigt. Der Körper
schwingt ungedämpft und harmonisch. Die Amplitude der Schwingungen ist
yˆ = 18 cm und die Schwingungsdauer ist T0 = 4,0 s .
Die Anfangsbedingungen für die Schwingungen sind:
Der Körper wird um y (0) = 18 cm aus seiner Ruhelage ausgelenkt und anschießend
ohne Anfangsgeschwindigkeit losgelassen.
(a) Bestimmen Sie Eigenfrequenz f0 und Eigenkreisfrequenz ω0 der ungedämpften
Schwingungen.
(b) Bestimmen Sie die Federkonstante c der Feder.
(c) Geben Sie das Weg-Zeit-Gesetz y (t ) für die beschriebenen Schwingungen an.
(d) Welche Auslenkung y (0,5 s) aus der Ruhelage und welche Geschwindigkeit
v (0,5 s) hat der Körper zum Zeitpunkt t = 0,5 s ?
(e) Welche maximale Geschwindigkeit v max hat der schwingende Körper?
(f) Bestimmen Sie die Gesamtenergie E ges des Feder-Masse-Systems.
Schwingungslehre
-1-
Prüfungsaufgabe 01
Schwingungslehre – Prüfungsaufgabe 01 – Kurzlösungen
π
(a) Eigenfrequenz f0 = 0,25 s −1 ; Eigenkreisfrequenz ω0 = s −1 .
2
(b) Federkonstante c = 0,123 N m −1 .
(c) Weg-Zeit-Gesetz y = 18 cm ⋅ cos(
π −1
s t).
2
(d) Zeitpunkt t = 0,5 s :
Auslenkung aus der Ruhelage
y (t = 0,5 s) = 12,73 cm ;
Geschwindigkeit
v (t = 0,5 s) = − 20,0 cm s −1 .
(e) Maximale Geschwindigkeit v max = 28,2 cm s −1 .
(f) Gesamtenergie E ges = 1,99 ⋅ 10 −3 J .
Schwingungslehre
-2-
Prüfungsaufgabe 01
Schwingungslehre – Prüfungsaufgabe 01 – Musterlösung
(a) Aus der Schwingungsdauer T0 erhält man für die Eigenfrequenz
1
1
f0 =
=
= 0,25 s −1
T0 4,0 s
und die Eigenkreisfrequenz
2π
2π
π
ω0 =
=
= s −1
T0
4,0 s 2
(b) Die Federkonstante c kann aus der Masse m des Körpers und der
Eigenkreisfrequenz ω0 des Federpendels bestimmt werden. Aus
ω0 2 =
c
m
wird
c = m ω0 2 = 50 ⋅ 10 − 3 kg ⋅
π2 − 2
s ⋅ (m ⋅ m −1 )
4
= 0,123 N m −1
(c) Für eine harmonische Schwingung lässt sich das Weg-Zeit-Gesetz darstellen als
y = yˆ cos(ω0 t + ϕ 0 )
oder
y = yˆ sin(ω0 t + ϕ0 )
Dabei ist die Eigenkreisfrequenz ω 0 eine für das schwingende System
charakteristische Größe. Amplitude ŷ und Nullphasenwinkel ϕ0 bestimmen sich aus
den Anfangsbedingungen; diese sind y (0) = 18 cm und v (0 ) = y& (0 ) = 0 .
Bei Auslenken des Körpers und anschließendem Loslassen ohne
Anfangsgeschwindigkeit kann die Auslenkung nie größer werden, als eben diese
Anfangsauslenkung, d. h. die Anfangsauslenkung muss gleich der Amplitude der
harmonischen Bewegung sein. In einer Beschreibung als Kosinus-Funktion wird
vereinfachend der Nullphasenwinkel gleich null. Damit kann man sofort schreiben
π
y = 18 cm ⋅ cos( s −1 t )
2
[Durch Ableiten und Bestimmen der Funktionswerte für den Zeitpunkt t = 0 können
Sie auch nachweisen, dass die vorgegebenen Anfangsbedingungen erfüllt sind.]
(d) Zum Zeitpunkt t = 0,5 s wird die Auslenkung des Körpers aus der Ruhelage
π
π
1
2
y (t = 0,5 s) = 18 cm ⋅ cos( s −1 ⋅ 0,5 s) = 18 cm ⋅ cos( ) = 18 cm ⋅
2
4
2
= 12,7 cm
die Geschwindigkeit ergibt sich als erste Ableitung des Weg-Zeit-Gesetzes zu
v = y& = − yˆ ω0 sin(ω0 t )
Zum Zeitpunkt t = 0,5 s wird die Geschwindigkeit des Körpers
Schwingungslehre
-3-
Prüfungsaufgabe 01
v (t = 0,5 s) = − 18 cm ⋅
1
π
π −1
s ⋅ sin( s −1 ⋅ 0,5 s) = − 28,3 cm s −1 ⋅
2
2
2
2
= − 20,0 cm s −1
Bei einer Anfangsauslenkung in die positive Koordinatenrichtung ist die
Geschwindigkeit in der ersten Viertelperiode auf die Ruhlage hin, also in negative
Koordinatenrichtung, gerichtet.
(e) Seine maximale Geschwindigkeit hat der Körper beim Nulldurchgang. Die
T
Nulllage wird nach einer Viertelschwingung, also nach t = 0 = 1,0 s erreicht. Man
4
erhält durch stures Einsetzen
v (t = 1 s) = − 18 cm ⋅
π
π −1
s ⋅ sin( s −1 ⋅ 1 s) = − 28,3 cm s −1 ⋅ 1
2
2
= − 28,3 cm s −1
Eine einfachere Argumentation lautet: Die Geschwindigkeit ist gegeben durch
v = y& = − yˆ ω0 sin(ω0 t )
Für den Betrag der Sinus-Funktion gilt
0 ≤ sin(ω0 t ) ≤ 1
deshalb ist der Betrag der maximalen Geschwindigkeit des Körpers gegeben durch
den Vorfaktor im Geschwindigkeit-Zeit-Gesetz
π
v max = yˆ ω0 = 18 cm ⋅ s −1 = 28,3 cm s −1
2
Eine alternative Lösung benutzt das Ergebnis von Teilaufgabe (f); sie wird im
Anschluss an Teilaufgabe (f) besprochen.
(f) Bei Loslassen zum Zeitpunkt t = 0 s ist die Anfangsgeschwindigkeit null und
damit auch die kinetische Energie des Körpers null.
Ekin ( y = yˆ ) = 0
Die Gesamtenergie des schwingenden Systems ist gleich der potentiellen Energie
der gespannten Feder zum Zeitpunkt des Loslassens, also bei maximaler
Auslenkung.
E ges = E pot ( y = yˆ ) =
1 2 1
cyˆ = ⋅ 0,123 N m −1 ⋅ (0,18 m) 2
2
2
= 1,99 ⋅ 10 − 3 N m
Schwingungslehre
-4-
Prüfungsaufgabe 01
Alternativer Lösungsweg zu Teilaufgabe (e)
Bei bekannter Gesamtenergie E ges und Masse m des Körpers kann die
Geschwindigkeit für den Nulldurchgang bestimmt werden. Bei entspannter Feder ist
die potentielle Energie der Feder
E pot ( y = 0) = 0
Die Gesamtenergie beim Nulldurchgang wird allein repräsentiert durch die kinetische
Energie
1
E ges = E kin ( y = 0) = mv max 2
2
v max 2 =
2E ges
m
=
2 ⋅ 1,99 ⋅ 10 −3 N m
50 ⋅ 10 − 3 kg
= 7,96 ⋅ 10 − 2 m 2 s − 2
und
v max = 0,282 m s −1 = 28,2 cm s −1
Die geringfügige Abweichung zum Ergebnis der Teilaufgabe (e) erklärt sich durch
Rundungsfehler.
Schwingungslehre
-5-
Prüfungsaufgabe 01
Schwingungslehre – Prüfungsaufgabe 02
Ein Körper (Masse m = 300 g ) hängt an einer idealen Feder (Federkonstante
c = 5,0 Nm −1 ). Nach einmaligem Anstoß führt das System schwach gedämpfte
Schwingungen aus. Man beobachtet, dass in zehn Schwingungsperioden die
Auslenkungen jeweils auf die Hälfte des Anfangswertes abklingen.
(a) Bestimmen Sie Eigenkreisfrequenz ω0 , Eigenfrequenz f0 und
Schwingungsdauer T0 des ungedämpften Systems.
(b) Bestimmen Sie den Abklingkoeffizient δ und den Dämpfungsgrad D des
gedämpften Systems.
(c) Welche Länge L muss ein Fadenpendel haben, um mit der Schwingungsdauer
des ungedämpften Federpendels zu schwingen?
(d) In einem Gedankenversuch werden die beiden Pendel auf den Mond gebracht.
Wie ändern sich die Schwingungsdauern von ungedämpftem Federpendel und
Fadenpendel jeweils im Vergleich zur ihrer Schwingungsdauer an der
Erdoberfläche?
(Für die Verhältnisse der Fallbeschleunigungen gilt g Erde : g Mond = 6 : 1)
Schwingungslehre
-1-
Prüfungsaufgabe 02
Schwingungslehre – Prüfungsaufgabe 02 – Kurzlösungen
(a) Eigenkreisfrequenz ω0 = 4,08 s −1; Eigenfrequenz f0 = 0,650 s −1 .
Schwingungsdauer T0 = 1,54 s .
(b) Abklingkoeffizient δ = 4,50 ⋅ 10−2 s−1 ; Dämpfungsgrad D = 1,10 ⋅ 10 −2 .
(c) Fadenlänge L = 58,9 cm .
(d) Federpendel: T0Mond = T0Erde (ungeändert).
Fadenpendel: T0Mond = 6 ⋅ T0Erde .
Schwingungslehre
-2-
Prüfungsaufgabe 02
Schwingungslehre – Prüfungsaufgabe 02 – Musterlösung
(a) Die Eigenkreisfrequenz ω0 des ungedämpften Systems erhält man aus
Federkonstante c und angehängter Masse m aus der Beziehung
ω0 2 =
c 5,0 N m −1 16,67 kg m s −2 ⋅ m −1
=
=
kg
m 0,300 kg
= 16,67 s − 2
damit wird
ω0 = 4,08 s −1
Für den Zusammenhang zwischen Eigenkreisfrequenz ω0 und Eigenfrequenz f0 gilt
ω0 = 2πf0
also
f0 =
ω0 4,08 s −1
=
2π
2π
= 0,650 s −1
Für den Zusammenhang zwischen Eigenkreisfrequenz ω0 und Schwingungsdauer
T0 gilt
ω 0 = 2π
1
T0
also
1
2π
=
ω0 4,08 s −1
= 1,54 s
T0 = 2π
(b) Die Schwingungen eines viskos gedämpften Feder-Masse-Systems lassen sich
darstellen als
y = yˆ 0 ⋅ e −δ t cos( ωdt + ϕ 0 )
oder
y = yˆ 0 ⋅ e −δ t sin( ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende
Exponentialfunktion zu untersuchen; also den Zeitverlauf von
y einh = yˆ 0 e −δt
oder
y einh
= e − δt
yˆ 0
Logarithmieren liefert
ln[
y einh
] = ln[e − δ t ] = − δ t
yˆ 0
Schwingungslehre
-3-
Prüfungsaufgabe 02
Unter der Annahme ’schwacher Dämpfung’, also 0 < D ≤ 0,1 gilt für die
Schwingungsdauern mit Dämpfung die Näherung Td ≈ T0 .
Für zehn Schwingungsperioden, also für das Zeitintervall t = 10 T0 , gilt für das
Verhältnis der Auslenkungen
p=
y einh 1
=
2
yˆ 0
Es wird also
1
ln[ ] = −δ ⋅ 10 ⋅ 1,54 s
2
Der Abklingkoeffizient ergibt sich daraus zu
δ=−[
ln(1) − ln(2)
0 − 0,693
]=−[
]
15,4 s
15,4 s
= 4,50 ⋅ 10 − 2 s −1
Der Dämpfungsgrad des gedämpften Systems bestimmt sich aus Abklingkoeffizient
δ und Eigenkreisfrequenz ω0 zu
D=
4,50 ⋅ 10 −2 s −1
δ
=
ω0
4,08 s −1
= 1,10 ⋅ 10 − 2
Mit 0 < D ≤ 0,1 liegt für das System schwache Dämpfung vor; die oben gemachte
Näherung Td ≈ T0 ist gerechtfertigt.
(c) Die Schwingungsdauer eines Fadenpendels (Fadenlänge L ) bei kleinen
Auslenkungen aus der Ruhelage nahe der Erdoberfläche (Fallbeschleunigung) g E
ist
T0 = 2π
L
g Erde
daraus erhält man für die Fadenlänge
L=
T0 2 g E
=
4π 2
= 58,9 cm
Schwingungslehre
(1,54 s)2 ⋅ 9,81 m s −2
4π 2
= 0,589 m
-4-
Prüfungsaufgabe 02
(d) Die Schwingungsdauer eines Feder-Masse-Systems hängt nur von den
Eigenschaften der Feder (Federkonstante c ) und der Masse m des angehängten
Körpers ab. Die Schwingungsdauer ändert sich deshalb bei Verbringen auf den
Mond nicht.
Die Schwingungsdauer eines Fadenpendels hängt von der Fallbeschleunigung ab
(vgl. Teilaufgabe (c)).
Es gilt für die Schwingungsdauern auf der Erde und auf dem Mond
T0Erde = 2π
L
und
gErde
T0Mond = 2π
L
g Mond
das Verhältnis der beiden Schwingungsdauern wird
T0Mond
T0Erde
2π
=
2π
L
g Mond
L
=
g Erde
=
g Mond
6 ⋅ g Mond
=
g Mond
6
1
g Erde
oder
T0Mond = 6 ⋅ T0Erde
Wie erwartet nimmt mit kleiner werdender Fallbeschleunigung die Schwingungsdauer
zu.
Schwingungslehre
-5-
Prüfungsaufgabe 02
Schwingungslehre – Prüfungsaufgabe 03
Ein Feder-Masse-System (Masse m = 400 g , Federkonstante c = 5,0 Nm −1 ) führt
viskos gedämpfte Schwingungen aus. Die Dämpfungskraft ist proportional zur
Geschwindigkeit des schwingenden Körpers. Bei einer Geschwindigkeit des Körpers
r
r
von v = 0,50 m s −1 ist der Betrag der Reibungskraft Freib = 0,25 N .
(a) Welche Schwingungsdauer T0 gehört zum ungedämpften System?
(b) Bestimmen Sie den Abklingkoeffizienten δ , den Dämpfungsgrad D und die
Schwingungsdauer Td des gedämpften Systems.
(c) Um welchen Bruchteil p nehmen die Auslenkungen in jeweils einer
Schwingungsperiode ab?
(d) Welcher Dämpfungskoeffizient baperiod muss für den aperiodischen Grenzfall
eingestellt werden?
Schwingungslehre
-1-
Prüfungsaufgabe 03
Schwingungslehre – Prüfungsaufgabe 03 – Kurzlösungen
(a) Eigenkreisfrequenz ω0 = 3,53 6 s −1 ; Schwingungsdauer T0 = 1,77 7 s .
(b) Dämpfungskoeffizient b = 0,50 kg s −1 .
Abklingkoeffizient δ = 0,625 0 s −1 .
Dämpfungsgrad D = 0,176 8 .
Kreisfrequenz (gedämpftes System) ωd = 3,48 0 s −1 .
Schwingungsdauer (gedämpftes System) Td = 1,80 6 s .
(c) Verhältnis der Auslenkungen p = 0,323 .
(d) Dämpfungskoeffizient baperiod = 2,83 kg s −1 .
Schwingungslehre
-2-
Prüfungsaufgabe 03
Schwingungslehre – Prüfungsaufgabe 03 – Musterlösung
(a) Für ein Feder-Masse-System legen Masse m des Körpers und Federkonstante
c die Eigenkreisfrequenz ω0 ungedämpfter Schwingungen eindeutig fest. Es gilt
ω0 2 =
c 5,0 N m −1 5,0 kg m s −2m −1
=
=
400 g
0,400 kg
m
= 12,50 s − 2
damit wird die Eigenkreisfrequenz
ω0 = 3,53 6 s −1
Daraus ergibt sich die Schwingungsdauer des ungedämpften Systems zu
T0 =
2π
2π
=
ω0 3,53 6 s −1
= 1,77 7 s
Alternative Vorgehensweise
Man bestimmt zuerst T0 und anschließend ω0 ; also
T0 = 2 π
0,400 kg
m
= 2π
c
5,0 kg m s − 2m −1
= 1,77 7 s
und
ω0 =
2π
2π
=
T0 1,78 s
= 3,53 6 s −1
(b) Bestimmung des Dämpfungskoeffizienten b eines geschwindigkeitsproportionalen Reibungsgesetzes. Für den Betrag der Reibungskraft gilt
r
r
Freib = b ⋅ v
also wird mit den gegebenen Werten der Dämpfungskoeffizient
r
Freib
0,25 N
0,25 kg m s − 2
b= r =
=
v
0,50 m s −1
0,50 m s −1
= 0,50 kg s −1
Der Abklingkoeffizient δ bestimmt sich aus Dämpfungskoeffizient b und Masse m
des Körpers zu
δ=
b
0,50 kg s −1
=
2m 2 ⋅ 0,400 kg
= 0,625 0 s −1
Schwingungslehre
-3-
Prüfungsaufgabe 03
Der Dämpfungsgrad D bestimmt sich aus Abklingkoeffizient δ und
Eigenkreisfrequenz ω0 zu
D=
0,625 0 s −1
δ
=
ω0
3,53 6 s −1
= 0,176 8
Mit D ≥ 0,1 liegt für das System starke Dämpfung vor.
Für die Kreisfrequenz eines viskos gedämpften Systems gilt mit Benutzung des
Abklingkoeffizienten δ die Beziehung
ω d 2 = ω0 2 − δ 2
= (3,53 6 s −1 ) 2 − (0,625 s −1 ) 2 = (12,50 3 − 0,3906) s − 2
= 12,10 9 s − 2
damit wird
ωd = 3,48 0 s −1
Alternativer Lösungsweg
Für die Kreisfrequenz eines viskos gedämpften Systems gilt mit Benutzung des
Dämpfungsgrads D
ωd = ω0 1 − D 2 = 3,53 6 s −1 ⋅ 1 − 0,176 8 2 = 3,53 6 s −1 ⋅ 0,984 2
= 3,48 0 s −1
Aus der Kreisfrequenz ωd ergibt sich die Schwingungsdauer Td des gedämpften
Systems
Td =
2π
2π
=
ωd 3,48 0 s −1
= 1,80 6 s
Zur Erinnerung: Die Schwingungsdauer T0 des ungedämpften Systems (vgl.
Teilaufgabe (a)) war
T0 = 1,77 7 s
(c) Die Schwingungen eines viskos gedämpften Feder-Masse-Systems lassen sich
darstellen als
y = yˆ 0 ⋅ e −δ t cos( ωdt + ϕ 0 )
oder
y = yˆ 0 ⋅ e −δ t sin( ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende
Exponentialfunktion zu untersuchen; also den Zeitverlauf von
y einh = yˆ 0 ⋅ e −δ t
Schwingungslehre
-4-
Prüfungsaufgabe 03
oder
y einh
= e−δ t
yˆ 0
Für das Verhältnis p der Auslenkungen im zeitlichen Abstand einer
Schwingungsperiode, also für t = Td , wird
p = e − δTd = e − (0,625 s
= 0,323
−1
) ⋅(1,80 6 s)
= e −1,13
(d) Für den aperiodischen Grenzfall ist der Dämpfungsgrad D = 1. Der aperiodische
Grenzfall steht zwischen dem Schwingfall mit D < 1 und dem Kriechfall mit D > 1 .
Wegen
δ
D=
=1
ω0
wird für den aperiodischen Grenzfall
δ = ω0
Damit wird der Dämpfungskoeffizient
baperiod = 2mω0 = 2 ⋅ 0,400 kg ⋅ 3,53 6 s −1
= 2,83 kg s −1
Schwingungslehre
-5-
Prüfungsaufgabe 03
Schwingungslehre – Prüfungsaufgabe 04
c
An einer idealen Schraubenfeder
(Federkonstante c = 0,1 N cm −1 ) hängt eine
flache Waagschale (Masse M = 100 g )
[vgl. Skizze].
m
M
(a) Welche statische Auslenkung y stat der Feder aus ihrer entspannten Lage bewirkt
die angehängte Waagschale?
Auf die Waagschale lässt man aus H = 20 cm eine kleine Knetkugel (Masse
m = 20 g ) fallen. Nach dem Aufprall bleibt die Kugel auf der Schale liegen.
(b) Welche Fallgeschwindigkeit v E hat die Knetkugel unmittelbar vor dem Aufprall?
(c) Welche gemeinsame Geschwindigkeit u0 haben Schale und Knetmasse
unmittelbar nach dem Aufprall?
Nach dem Aufprall beobachtet man ungedämpfte harmonische Schwingungen des
beschriebenen Systems.
(d) Welche Schwingungsdauer T0 hat das schwingende System?
Rechnen Sie bitte vereinfachend mit g = 10 m s −2 .
Schwingungslehre
-1-
Prüfungsaufgabe 04
Schwingungslehre – Prüfungsaufgabe 04 – Kurzlösungen
(a) Statische Auslenkung y stat = 10 cm .
(b) Fallgeschwindigkeit bei Aufprall v E = 2,0 m s −1 .
(c) Gemeinsame Geschwindigkeit nach Aufprall u 0 = 0,333 m s −1 .
(d) Schwingungsdauer T0 = 0,688 s .
Schwingungslehre
-2-
Prüfungsaufgabe 04
Schwingungslehre – Prüfungsaufgabe 04 – Musterlösung
(a) Für ein lineares Kraftgesetz ist nach HOOKE die Auslenkung proportional zur
angreifenden Kraft
Fext = c y
(die äußere (externe) Kraft wirkt in Richtung der Auslenkung);
damit ist im Gleichgewicht die rücktreibende Kraft der Feder Frück = − c y
Die äußere Kraft ist die auf die Waagschale wirkende Gewichtskraft
Fext = FG = mg
Für die statische Auslenkung aus der Ruhelage der entspannten Feder gilt also
m g = c y stat
damit
y stat =
0,1 kg ⋅ 10 m s −2
m g 0,1 kg ⋅ 10 m s −2
=
=
= 1,0 ⋅ 10 −1 m
−
1
−
2
−
2
−
1
c
0,1 N cm
0,1 kg m s (10 m)
= 10 cm
(b) Die Geschwindigkeit der Knetkugel beim Aufprall ergibt sich – natürlich alles
ohne Luftreibungskräfte – aus dem Energiesatz in der Fassung der Mechanik. Dieser
liefert für den Zeitpunkt
•
des Loslassens
E kin (Anfang) = 0
E pot (Anfang) = m g H
1
m vE2
E pot (Ende) = 0
2
der Energieerhaltungssatz liefert also die Beziehung
•
des Aufpralls
mgH =
E kin (Ende) =
1
m vE2
2
damit
v E 2 = 2gH = 2 ⋅ 10 m s −2 ⋅ 0,20 m = 4,0 m 2 s -2
und
v E = 2,0 m s −1
Lösungsvariante (Anwendung kinematischer Beziehungen)
Es gelten ohne Luftreibung die Gesetze des ’freien Falls‘ mit der konstanten
Fallbeschleunigung g = const. ; allgemein
1 2
gt + v 0 t + h0
2
•
Weg-Zeit-Gesetz:
h=
•
Geschwindigkeit-Zeit-Gesetz:
v = gt + v 0
Speziell mit den Bedingungen h0 = 0 (Anfangskoordinate im Nullpunkt)
und v 0 = 0 (‘ohne Anfangsgeschwindigkeit‘) erhält man
Schwingungslehre
-3-
Prüfungsaufgabe 04
1 2
und
v = gt
gt
2
Beide Beziehungen miteinander kombiniert liefern
h=
h=
1 v2 1v2
g
=
2 g2 2 g
für h = H und v = v E also
v E 2 = 2gH
(c) Die Aussage “die Knetkugel bleibt nach dem Stoß auf der Waagschale liegen“
bedeutet; dass sich beide Körper unmittelbar nach dem Stoß mit gleicher,
einheitlicher Geschwindigkeit bewegen. Damit liegt – nach der Definition – ein
vollständig inelastischer Stoß vor. Da nur innere Kräfte wirken gilt der
Impulserhaltungssatz; also
’Impuls der Kugel vor Aufprall’ = ’Impuls des Systems nach Aufprall’, also
mv E = (M + m ) u 0
dabei ist u0 die gemeinsame Anfangsgeschwindigkeit der beiden, aneinander
haftenden, Körper unmittelbar nach Aufprall der Knetkugel. Damit wird
u0 =
20 g
m
⋅ 2,0 m s −1
vE =
(M + m )
(100 + 20) g
= 0,333 m s −1
(d) Die Schwingungsdauer T0 des Feder-Masse-Systems wird eindeutig durch die
Kenngrößen des schwingungsfähigen Systems bestimmt; diese sind
•
Federkonstante c und
•
Gesamtmasse (M + m ) des angehängten Körpers.
Für Eigenkreisfrequenz ω0 und Schwingungsdauer T0 gelten die Beziehungen
ω0 2 =
c
(M + m )
bzw. gleichberechtigt – mit ω0 =
T0 = 2π
2π
T0
(M + m )
c
die Schwingungsdauer wird
T0 = 2 π
(M + m )
0,120 kg
= 2π
c
0,1 kg m s − 2 (10 − 2 m) −1
= 0,688 s
Schwingungslehre
-4-
Prüfungsaufgabe 04
Schwingungslehre – Prüfungsaufgabe 05
m
Eine kleine Kugel (Masse m = 100 g )
fällt aus der Höhe h = 20 cm auf eine
entspannte und (idealisierend)
masselose Feder (Federkonstante
c = 20 N m -1 ) (vgl. Abb. A; die Feder
soll reibungsfrei in einem Zylinder
geführt werden).
Die Kugel m haftet auf der Feder und
führt harmonische Schwingungen
aus.
Von Reibungseinflüssen ist
abzusehen.
h
y =0
y0
y max
+y
Abb. A
Abb. B
Abb. C
Abb. D
(a) Um welche maximale Strecke y = y max (vgl. Abb. C) wird die ursprünglich
entspannte Schraubenfeder zusammengedrückt?
(b) Mit welcher Frequenz f0 schwingt das Feder-Masse-System?
(c) Um welche Gleichgewichtslage y = y 0 (vgl. Abb. D) erfolgt die Schwingung?
(d) Bestimmen Sie die Amplitude ŷ der Schwingung.
(e) Wie lauten die Anfangsbedingungen y (0 ) und y& (0) für den Zeitpunkt t = 0 des
Auftreffens der Kugel auf die entspannte Feder?
(f) Skizzieren Sie den qualitativen Verlauf der Schwingung y(t) in einem
y,t-Diagramm.
(g) Geben Sie formelmäßig die Funktion y(t) für diese Schwingung an; legen Sie
dabei die in Abb. B festgelegte y-Achse zu Grunde.
Berechnen Sie den Nullphasenwinkel der Schwingung y(t) aus den
Anfangsbedingungen. Hinweis: Der Nullphasenwinkel liegt im 3. Quadranten.
Schwingungslehre
-1-
Prüfungsaufgabe 05
Schwingungslehre – Prüfungsaufgabe 05 – Kurzlösungen
(a) Maximale Auslenkung y max = 19,8 cm .
(b) Eigenkreisfrequenz ω0 = 14,1 s −1 ; Eigenfrequenz f0 = 2,25 Hz .
(c) Statische Gleichgewichtslage y 0 = 4,9 cm .
(d) Amplitude yˆ = y max − y 0 = 14,8 cm .
(e) Anfangsauslenkung y (0) = 0 .
Anfangsgeschwindigkeit = Geschwindigkeit bei Aufprall y& (0) = v 0 = 1,98 ms −1 .
(f)-(g) Nullphasenwinkel ϕ 0 = 4,38 ( ϕ 0 = 251 o im Gradmaß).
Bewegungsgleichung y (t ) = 4,9 cm + 14,8 cm ⋅ cos(14,1 s −1 ⋅ t + 4,38) .
Schwingungslehre
-2-
Prüfungsaufgabe 05
Schwingungslehre – Prüfungsaufgabe 05 – Musterlösung
(a) Die Fallhöhe der Kugel bis zur maximalen Stauchung ist (h + y max ) . Daraus
ergibt sich die Absenkung der potentiellen Energie der Lage
Lage
Epot
= mg (h + y max )
die in der Feder bei maximaler Stauchung gespeicherte potentielle Energie ist
1
cy max 2
2
Aus dem Energieerhaltungssatz folgt
Feder
E pot
=
mg (h + y max ) =
1
cy max 2
2
Dies liefert eine quadratische Gleichung für y max
1 2
cy max − mgy max − mgh = 0
2
Mit der Mitternachtsformel folgt
mg ± m 2 g 2 + 2mghc
c
Umformung liefert (jeder Term des Zählers wird durch c dividiert; unter dem
Wurzelzeichen also durch c 2 )
y max 1 / 2 =
2
y max 1 / 2
mg
m 2g 2
mg mg
⎛ mg ⎞
⎛ mg ⎞
=
±
+ 2h
=
± ⎜
⎟ + 2h⎜
⎟
2
c
c
c
⎝ c ⎠
⎝ c ⎠
c
Die negative Lösung ist wegen
2
⎛ mg ⎞
⎛ mg ⎞ ⎛ mg ⎞
⎜
⎟ + 2h⎜
⎟ >⎜
⎟
⎝ c ⎠
⎝ c ⎠ ⎝ c ⎠
physikalisch sinnlos, also bleibt
2
y max
mg
⎛ mg ⎞
⎛ mg ⎞
=
+ ⎜
⎟ + 2h ⎜
⎟
c
⎝ c ⎠
⎝ c ⎠
die vorgegebenen Werte eingesetzt, erhält man für die auftretende Größe
mg
c
mg
m
1
= 0,1 kg ⋅ 9,81
⋅
= 49,1 ⋅ 10 -3 m
2
2
1
−
−
c
s 20 (kg m s ) m
= 4,9 cm
damit wird schließlich die maximale Auslenkung
y max = 0,049 m + 0,049 2 m 2 + 2 ⋅ 0,2 m ⋅ 0,049 m
= 0,049 m + 2,20 ⋅ 10 - 2 m 2 = 0,049 m + 0,148 m = 0,198 m
= 19,8 cm
Schwingungslehre
-3-
Prüfungsaufgabe 05
(b) Die Eigenkreisfrequenz ω0 eines Feder-Masse-Systems bestimmt sich aus der
Federkonstante c und der Masse m des angehängten Körpers zu
c
=
m
ω0 =
20 (kg m s − 2 ) m −1
0,1 kg
= 14,1 s −1
Die Eigenfrequenz f0 wird
2π
2π
=
ω0 14,1 s −1
= 2,25 Hz
f0 =
(c) Die gesuchte Gleichgewichtslage ist die ’statische
Gleichgewichtslage‘, d. h. es
r
r
kompensieren sich rücktreibende Federkraft Frück und Gewichtskraft Fgrav auf die
Kugel. Für die Beträge gilt
•
Gewichtskraft auf die Kugel
•
rücktreibende Federkraft
r
Fgrav = mg und
r
Frück = c y 0
Damit
m g = c y0
Dies liefert
y0 =
mg
0,1kg ⋅ 9,81ms −2
=
= 0,049 m
c
20 (kg m s - 2 ) ⋅ m -1
= 4,9 cm
(d) Die gesuchte Amplitude der Schwingung ist damit
yˆ = y max − y 0 = 19,8 cm − 4,9 cm = 14,8 cm
(e) Die Anfangsbedingungen für die Schwingungen sind
y(0) = 0 die entspannte Lage der Feder und
y& (0) = v 0 die Geschwindigkeit der aufprallenden Kugel.
Der Energieerhaltungssatz liefert mit der Fallhöhe h und der Geschwindigkeit v 0 bei
Aufprall
1
m g h = m v 02
2
und
v 0 = 2 g h = 2 ⋅ 9,81 ms − 2 ⋅ 0,2 m = 3,92 m 2 s − 2
= 1,98 ms −1
Schwingungslehre
-4-
Prüfungsaufgabe 05
(f)-(g) Damit ergibt sich die Bewegungsgleichung für die schwingende Kugel
y (t ) = y 0 + yˆ cos(ω0 t + ϕ 0 )
dabei sind vorgegeben oder wurden bereits bestimmt
y 0 = 4,9 cm
yˆ = 14,8 cm
ω0 = 14,1 s −1
v 0 = 1,98 ms −1
Bestimmung des Nullphasenwinkels ϕ 0
Zunächst wird gezeigt, dass ϕ0 im 3. Quadranten liegt; dieser Beweis wurde in der
Prüfung nicht verlangt, man durfte den Hinweis in der Aufgabenstellung benutzen.
Es gilt allgemein (Darstellung der Schwingung als Kosinus-Funktion)
y (t ) = y 0 + yˆ cos(ω0 t + ϕ 0 )
• für die Auslenkung
•
und die Geschwindigkeit
y& (t ) = − yˆω0 sin(ω0 t + ϕ 0 )
Zum Zeitpunkt t = 0 des Aufpralls ist
•
die Auslenkung
y (0 ) = 0
•
die Geschwindigkeit
v (0) = y& (0) = v 0
Diese speziellen Anfangsbedingungen eingesetzt, ergibt
y 0 + yˆ cos ϕ 0 = 0
und
− yˆ ω0 sin ϕ0 = v 0
Die erste dieser Gleichungen liefert
cos ϕ 0 = −
y0
4,9 cm
=−
yˆ
14,8 cm
= − 0,331
die zweite dieser Gleichungen liefert
− yˆ ω0 sin ϕ0 = v 0
oder
sin ϕ0 = −
v0
198 cm s −1
=−
yˆω0
14,8 cm ⋅ 14,1s −1
= − 0,949
Weil für den Nullphasenwinkel ϕ0 sowohl die Kosinusfunktion als auch die
Sinusfunktion ein negatives Vorzeichen haben ( cos ϕ 0 < 0 und sin ϕ < 0 ) muss ϕ0
notwendig im 3. Quadranten liegen.
Schwingungslehre
-5-
Prüfungsaufgabe 05
Der Tangens des gesuchten Nullphasenwinkels ergibt sich aus den berechneten
Werten der Sinus- und der Kosinus-Funktion zu
tan ϕ 0 =
sin ϕ 0
− 0,949
=
cos ϕ 0 − 0,331
= 2,87
Macht man von dem Lösungshinweis gebrauch, dass der Nullphasenwinkel im 3.
Quadranten liegt, dann ist der schnellere Weg zum gleichen Ergebnis der Folgende.
Man nimmt die auf die Anfangsbedingungen (siehe oben) angepassten Gleichungen
yˆ cos ϕ0 = − y 0
(1)
− yˆ ω0 sin ϕ0 = v 0
(2)
Division der zweiten Gleichung durch die erste Gleichung ergibt sofort
v0
sin ϕ 0
yˆω0
v0
198 cm s −1
tan ϕ 0 =
=
=
=
y0
cos ϕ 0
ω0 y 0 14,1s −1 ⋅ 4,9 cm
−
yˆ
−
= 2,87
Mit der Bedingung
3π
π
( ϕ0 im 3. Quadrant) erhält man
≤ ϕ0 ≤
2
2
ϕ 0 = 251 o im Gradmaß oder ϕ 0 = 4,38 im Bogenmaß
Damit erhält man letztlich die Bewegungsgleichung für die ungedämpften
Schwingungen der Kugel
y (t ) = 4,9 cm + 14,8 cm ⋅ cos(14,1 s −1 ⋅ t + 4,38)
Probe: Für den Zeitpunkt t = 0 , also dem Aufprall der Kugel wird
y (0) = 4,9 cm + 14,8 cm ⋅ cos( 4,38 )
= 4,9 cm + 14,8 cm ⋅ ( − 0,33) = 4,9 cm − 4,8 cm
= 0,1 cm ≈ 0 cm
Die geringfügige Abweichung erklärt sich durch Rundungsfehler im Verlauf der
Berechnung
und
y& (0) = −14,8 cm ⋅ 14,1 s −1 ⋅ sin( 4,38) = −14,8 cm ⋅ 14,1 s −1 ⋅ ( −0,945)
= 197 cm s −1
Geringfügige Abweichungen erklären sich durch Rundungsfehler im Verlauf der
Berechnungen.
Schwingungslehre
-6-
Prüfungsaufgabe 05
Schwingungslehre – Prüfungsaufgabe 06
Um die Masse eines Astronauten während eines
längeren Aufenthalts in einer Raumstation zu
kontrollieren, wird für die Raumstation SKYLAB
das folgende physikalische Messverfahren
benutzt:
Zunächst wird ein Sitz der Masse mS = 12,5 kg
durch eine Feder (Federkonstante c) an eine
Wand der Raumstation gekoppelt und auf
Schienen so geführt, dass der Sitz harmonische
Schwingungen ausführen kann. Die dabei
beobachtete Periodendauer ist T0,S = 0,35 s .
c
mS
Anschließend wird ein Astronaut in den Sitz
geschnallt und das System erneut in
Schwingungen versetzt. Man misst nun eine
Schwingungsdauer T0,S + A = 0,90 s .
(a) Bestimmen Sie aus diesen Messwerten die Masse m A des Astronauten.
(b) Ein Mitastronaut muss die Schwingungen anregen. Welche Arbeit W muss er
aufwenden, damit sich für eine ungedämpfte Schwingung eine
Schwingungsamplitude yˆ =10 cm einstellt?
(c) Bestimmen Sie die größte Geschwindigkeit v max , die der Astronaut während der
Schwingungsbewegungen erreicht?
(d) Infolge schwacher Dämpfung gehen die Auslenkungen in N = 10 Schwingungen
auf jeweils zwei Drittel des Anfangswertes zurück. Welchen Dämpfungsgrad D hat
das schwingende System?
Hinweis: Die Masse der Raumstation ist so groß, dass die Station als Inertialsystem
betrachtet werden darf.
Schwingungslehre
-1-
Prüfungsaufgabe 06
Schwingungslehre – Prüfungsaufgabe 06 – Kurzlösungen
(a) Masse Astronaut mA = 70,2 kg .
Feder
(b) Aufgewendete Arbeit W = E pot
(max) = 20,2 J .
(c) Größte Geschwindigkeit v max = 0,70 m s −1 .
(d) Abklingkoeffizient δ = 4,50 ⋅ 10−2 s−1 ; Dämpfungsgrad D = 6,5 ⋅ 10 −3 .
Schwingungslehre
-2-
Prüfungsaufgabe 06
Schwingungslehre – Prüfungsaufgabe 06 – Musterlösung
(a) Für eine ungedämpfte Schwingung eines Feder-Masse-Systems gilt für die
Schwingungsdauer
M
c
T0 =2π
Dabei ist M die Masse des angehängten Körpers und c die Federkonstante der
(linearen) Federcharakteristik.
Für die beiden Schwingungsversuche gilt somit (Indices ‘S’ - Sitz und ‘A’ - Astronaut)
mS
c
T0,S =2π
T0,S + A =2π
bzw.
( mS + m A )
c
Mit dem ersten Schwingungsversuch wird experimentell bei bekannter Masse mS die
Federkonstante c bestimmt; aus der Beziehung für die Schwingungsdauer T0, S erhält
man
mS
c = 4π 2
T0, S
2
= 4π 2
12,5 kg
(0,35 s)
2
⋅
m
m
= 4,03 ⋅ 10 3 Nm -1
Man braucht aber die Federkonstante c aus der ersten Gleichung (Schwingung des
Sitzes allein) gar nicht explizit auszurechen. Da die Feder für beide Versuche die
gleiche ist, fällt bei der Division der beiden Schwingungsdauern T0, S + A und T0, S die
Federkonstante c heraus; quadrieren ergibt
(T0,S + A ) 2
(T0,S )
2
=
( mS + m A )
mS
daraus erhält man für die Masse des Astronauten
mA = [
(T0,S + A ) 2
(T0,S ) 2
− 1]mS = [
(0,90 s) 2
(0,35 s) 2
− 1]⋅ 12,5 kg = [ 6,61 − 1] ⋅12,5 kg
= 70,2 kg
(b) Die vom Mitastronauten aufgewendete Arbeit W wird (1) in potentielle Energie der
Feder und (2) in kinetische Energie des schwingenden Systems (Astronaut + Sitz)
umgesetzt. Im Umkehrpunkt der Schwingung, also bei Maximalauslenkung (=
Amplitude) die kinetische Energie des schwingenden Systems
S+ A
Ekin
= 0 weil im Umkehrpunkt der Schwingung die Geschwindigkeit null ist.
Es ist nur die potentielle Energie der Feder zu berücksichtigen. Diese hängt quadratisch
von der Auslenkung ab, also ergibt sich für die Amplitude ŷ
1
1
N
Feder
W = E pot
= c yˆ 2 = ⋅ 4,03 ⋅ 10 3
⋅10 − 2 m 2
2
2
m
= 20,2 J
Schwingungslehre
-3-
Prüfungsaufgabe 06
(c) Variante 1
Beim Nulldurchgang der Schwingung ist die potentielle Energie der Feder
Feder
E pot
=0
weil die Auslenkung null ist.
Die kinetische Energie der beiden schwingenden Körper beim Nulldurchgang ist
1
S+A
E kin
(max) = (mS + m A ) v max 2
2
Sie ist gleich der Gesamtenergie, also
1
S+ A
W = E kin
(max) = (mS + m A ) v max 2
2
daraus erhält man
v max 2 =
2W
2 ⋅ 20,2 N m
=
= 0,489 m 2 s − 2
( mS + m A )
82,7 kg
v max = 0,70 m s −1
(c) Variante 2
Das Weg-Zeit-Gesetz einer ungedämpften harmonischen Schwingung lässt sich durch
eine Sinus- oder eine Kosinus-Schwingung darstellen. Die Geschwindigkeit erhält man
als erste Ableitung des Weg-Zeit-Gesetzes nach der Zeit
Darstellung als Sinus-Funktion
Darstellung als Kosinus-Funktion
Weg-Zeit-Gesetz
y (t ) = yˆ sin(ω0 t + ϕ 0 )
y (t ) = yˆ cos(ω0 t + ϕ0 )
Geschwindigkeit-Zeit-Gesetz
y& (t )= yˆ ω0 cos(ω0 t + ϕ0 )
y& (t )= − yˆ ω0 sin(ω0 t + ϕ0 )
dabei ist die Eigenkreisfrequenz ω 0 des schwingenden Systems
ω0 =
2π
2π
=
T0 0,90 s
= 7,0 s − 1
und die Amplitude
yˆ = 10 cm
Da der Betrag einer harmonischen Funktion maximal den Wert 1 annehmen kann, also
wegen
0 ≤ sin(ω0 t + ϕ0 ) ≤ 1
0 ≤ cos (ω0 t + ϕ0 ) ≤ 1
ist der Vorfaktor im Geschwindigkeit-Zeit-Gesetz der Betrag der maximal auftretenden
Geschwindigkeit v max
v max = yˆω0 = 10 −1 m⋅ 6,98 s −1
= 0,70 m s −1
Schwingungslehre
-4-
Prüfungsaufgabe 06
(d) Die Schwingungen eines viskos gedämpften Feder-Masse-Systems lassen sich
darstellen als
y = yˆ 0 ⋅ e −δ t cos(ωdt + ϕ 0 )
oder
y = yˆ 0 ⋅ e −δ t sin(ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende
Exponentialfunktion zu untersuchen; also den Zeitverlauf von
y einh = yˆ 0 ⋅ e −δt
oder
y einh
= e − δt
yˆ 0
Logarithmieren liefert
ln[
y einh
] = ln[e − δ t ] = − δ t
ˆ
y0
Unter der, später zu überprüfenden, Annahme für den Dämpfungsgrad 0 < D ≤ 0,1 wird
mit Td ≈ T0 für das Zeitintervall t =10⋅ T0 das Verhältnis der Auslenkungen
p=
y einh 2
=
3
yˆ 0
Es wird also
2
ln[ ] = − δ ⋅ 10 ⋅ 0,90 s
3
Der Abklingkoeffizient ergibt sich daraus zu
ln(2) − ln(3)
0,693 − 1,099
δ=−[
]=−[
]
9,00 s
9,00 s
= 4,50 ⋅ 10 − 2 s −1
Der Dämpfungsgrad ist definiert als
δ
4,50 ⋅ 10 −2 s −1
D=
=
= 0,0065 = 6,5 ⋅ 10 − 3
−
1
ω0
7,0 s
Damit ist auch die oben gemachte Annahme einer ‘schwachen Dämpfung’, also dir
Forderung D ≤ 0,1, erfüllt.
Schwingungslehre
-5-
Prüfungsaufgabe 06
Schwingungslehre – Prüfungsaufgabe 07
Ein schwingungsfähiges System besteht aus einem gespannten Faden, an dem eine
kleine Kugel befestigt ist. Der Faden wird über zwei Rollen geführt und durch die
Gewichtskraft eines Körpers ‘2‘ gespannt (vgl. Skizze). Die Kugel befindet sich genau
in der Mitte des senkrechten Teils des Fadens. Die Kugel soll nur horizontale Bewegungen ausführen können.
Machen Sie zur Lösung des Schwingungsproblems folgende vereinfachende Annahmen
•
die Schwingungsamplitude sei sehr klein,
•
Körper ‘2‘ soll sich nicht mitbewegen und
•
der Einfluss des Körpers ‘1‘ auf die Seilkraft sei vernachlässigbar.
Im Faden herrscht damit überall eine konstante Seilkraft.
Kugel
Masse m1 = 5 g
Radius r = 4 mm
m1
L
s
m2
Körper ‘2‘
Masse m2 = 0,60 kg
Faden
Länge
L = 30 cm
(a) Geben Sie die rücktreibende Kraft Frück auf die Kugel in Abhängigkeit von einer
kleinen horizontalen Verschiebung s an.
(b) Stellen Sie die Differentialgleichung für diese freie, ungedämpfte Schwingung auf.
Berechnen Sie die Eigenkreisfrequenz ω0 .
Anschließend wird der schwingende Teil des Systems mit der kleinen Kugel in eine
Flüssigkeit eingetaucht. Die Schwingungen sind nun gedämpft. Die dynamische Viskosität der Flüssigkeit bei Versuchstemperatur ist η = 0,02 Pa ⋅ s .
(c) Berechnen Sie die Abklingkonstante δ und den Dämpfungsgrad D unter der Annahme viskoser Reibung (also laminarer Umströmung der Kugel). Der Strömungswiderstand des Fadens ist vernachlässigbar.
(d) Wie lange dauert es, bis die Amplituden der Schwingungen jeweils auf ein Zehntel abgeklungen sind?
Schwingungslehre
-1-
Prüfungsaufgabe 07
Schwingungslehre – Prüfungsaufgabe 07 – Kurzlösungen
2
(a) Rücktreibende Kraft (linearisiert) Frück ≅ − (2 m2 g ) ⋅ s .
L
(b) Differentialgleichung (linearisiert) s&& + (
4 m2 g
)s = 0 .
m1 L
Eigenkreisfrequenz ω0 = 125 s −1 .
(c) Abklingkonstante δ = 0,151 s −1 .
Dämpfungsgrad D = 1,2 ⋅ 10 −3 .
(d) Zeitintervall t * = 15,2 s .
Schwingungslehre
-2-
Prüfungsaufgabe 07
Schwingungslehre – Prüfungsaufgabe 07 – Musterlösung
(a) Die (näherungsweise) konstante Kraft FF im Faden ist gleich der Gewichtskraft
auf den Körper ‘2‘; also gegeben durch
FF ≅ m2 g
Wird Körper ‘1‘ in horizontaler Richtung ausgelenkt, dann wird die rücktreibende Kraft
auf die Kugel
Frück = − 2 FF sin β ≅ − 2 FF β
Unter der einschränkenden Voraussetzung kleiner Auslenkungen ist der Winkel
β << 1 und es gilt näherungsweise sin β ≅ β .
Die Geometrie liefert für den Zusammenhang zwischen horizontalem Weg s und
Auslenkwinkel β
L
L
tan β ≅ β
2
2
Unter der Voraussetzung β << 1 gilt näherungsweise tan β ≅ β .
s=
Zusammengenommen ergibt sich die rücktreibende Kraft
auf die Kugel zu
2
Frück ≅ − (2 m2 g ) ⋅ s
L
diese Beziehung ist ein lineares Kraftgesetz und erfüllt damit
die notwendige Voraussetzung für eine harmonische Bewegung.
β
FF
Frück
FF
(b) Nach NEWTON bewirkt eine Kraft auf einen Körper
dessen Beschleunigung gemäß
F = m1 a = m1
d2s
dt 2
Damit ergibt sich – mit der Einschränkung ’kleine Auslenkwinkel’, also β << 1 –
die linearisierte Differentialgleichung für die Bewegung der Kugel als harmonische
Schwingung zu
m1
d2s
dt 2
=−
4 m2 g
s
L
oder
s&& + (
4 m2 g
)s = 0
m1 L
Durch Koeffizientenvergleich mit der Standard-Differentialgleichung
x&& + ω0 2 x = 0
Schwingungslehre
-3-
Prüfungsaufgabe 07
erhält man für das Quadrat der Eigenkreisfrequenz
ω0 2 =
4 m2 g 4 ⋅ 0,6 kg ⋅ 9,81 m s −2
=
= 15 700 s −1
−
3
m1 L
0,3 m ⋅ 5 ⋅ 10 kg
und
ω0 = 125 s −1
(c) Bei viskoser Reibung gilt ein geschwindigkeitsproportionales Reibungsgesetz
FR = − b v
für eine laminare Umströmung einer Kugel gilt nach STOKES für die Reibungskraft
FR (Stokes) = − (6π η r ) v
also gilt für die Dämpfungskonstante
b = 6π η r
Die Differentialgleichung einer geschwindigkeitsproportional gedämpften Schwingung
lautet
b &
s&& +
s + ω0 2 s = 0
m1
Die Abklingkonstante δ bestimmt sich zu
δ=
b
6πηr 3π ⋅ 2 ⋅ 10 −2 N m −2 s ⋅ 4 ⋅ 10 −3 m
=
=
2 m1 2 m1
5 ⋅ 10 − 3 kg
= 0,151 s −1
Der (dimensionslose) Dämpfungsgrad D ist definiert als der Quotient aus Abklingkoeffizient δ und Eigenkreisfrequenz ω0
151⋅ 10 −3 s −1
δ
D=
=
ω0
125 s −1
= 1,2 ⋅ 10 − 3
(d) Die Schwingungen eines viskos gedämpften Systems lassen sich darstellen als
y = yˆ 0 ⋅ e −δ t cos( ωdt + ϕ 0 )
oder
y = yˆ 0 ⋅ e −δ t sin( ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende Exponentialfunktion zu untersuchen; also den Zeitverlauf von
y einh = yˆ 0 ⋅ e −δt
oder
y einh
= e − δt
yˆ 0
Schwingungslehre
-4-
Prüfungsaufgabe 07
Logarithmieren liefert
⎞
⎛y
ln⎜⎜ einh ⎟⎟ = ln(e − δ t ) = − δ t
⎝ yˆ 0 ⎠
Für das Abklingen im Zeitintervall t * auf jeweils ein Zehntel einer Anfangsauslenkung ergibt sich
ln[
1
] = − 0,151 s −1 ⋅ t *
10
damit
t* =
ln(1) − ln(10)
( − 0,151 s −1 )
= 15,2 s
Schwingungslehre
=
0 − 2,30
( − 0,151 s −1 )
-5-
Prüfungsaufgabe 07
Schwingungslehre – Prüfungsaufgabe 08
Eine homogene Scheibe aus Stahl wird an einen Stab befestigt. Die Anordnung kann
Pendelschwingungen um den Aufhängepunkt A ausführen (vgl. Skizze).
A
Scheibe
Radius
•
L
R
R = 3 cm
Masse msch = 0,2 kg
Stab
Länge
L = 0,5 m
Masse
mst = 0,3 kg
Die axialen Massenträgheitsmomente für Scheibe bzw. Stab senkrecht zur
Zeichenebene durch den jeweiligen Schwerpunkt S sind gegeben durch
1
1
m sch R 2
J st (S) =
m st L2
2
12
Berechnen Sie die beiden Schwingungsdauern T0a und T0b für jeweils ungedämpfte
Schwingungen bei kleinen Amplituden unter folgenden Modell-Annahmen:
(a) Die Masse des Stabs wird vernachlässigt.
(b) Unter Berücksichtigung der Massenverteilung des Stabs.
Hinweis: Berechnen Sie zunächst die Schwerpunktskoordinate des
Gesamtsystems aus Scheibe und Stab.
J sch (S) =
(c) Um welchen Prozentsatz weichen die Schwingungsdauern T0a und T0b in den
beiden Modellen voneinander ab?
Schwingungslehre
-1-
Prüfungsaufgabe 08
Schwingungslehre – Prüfungsaufgabe 08 – Kurzlösungen
(a) Massenträgheitsmoment J A = J sch (S) + msch L2 ≈ 0,05009 kg m 2 .
Schwingungsdauer T0phys = T0a = 1,42 s .
(b) Gemeinsamer Schwerpunkt Abstand von Drehpunkt A: y S = 0,35 m .
Massenträgheitsmoment (STEINER)
J A∗ = J st ( A ) + J sch ( A ) ≈ J st ( A ) + msch L2 = 0,0750 kg m 2 .
J st ( A ) = 0,0250 kg m 2 .
Schwingungsdauer T0b = 1,32 s .
(c) Abweichung
Schwingungslehre
ΔT T0b − T0a
=
= 0,076 oder 7,6 % .
T0b
T0b
-2-
Prüfungsaufgabe 08
Schwingungslehre – Prüfungsaufgabe 08 – Musterlösung
Beide Modelle stellen physikalische Pendel dar. Räumlich ausgedehnte Körper sind
im Schwerefeld der Erde schwingungsfähig aufgehängt. Das Schwingungsverhalten
wird jeweils durch das Massenträgheitsmoment der Modell-Anordnung bestimmt.
Für ein physikalisches Pendel ist die Schwingungsdauer bei kleinen Auslenkungen
aus der Ruhelage gegeben durch
T0phys = 2π
JA
mg d
mit m Gesamtmasse
g Schwerebeschleunigung
d Abstand Drehpunkt A – Massenmittelpunkt S
J A Massenträgheitsmoment bezüglich des Drehpunkts A
(a) Ohne Berücksichtigung des Stabs geht nur das Massenträgheitsmoment der
Scheibe in die Schwingungsdauer ein.
Der Satz von STEINER liefert das Massenträgheitsmoment J A der Scheibe bezüglich
des Drehpunkts A
J A = J sch (S) + msch L2 =
=
1
msch R 2 + msch L2
2
1
(0,2 kg)(0,03 m) 2 + (0,2 kg)(0,5 m) 2 = 0,009⋅ 10 − 2 kg m 2 + 5,00⋅10 − 2 kg m 2
2
≈ 0,05009 kg m 2
Für die Schwingungsdauer des physikalischen Pendels ergibt sich
T0phys = T0a = 2π
JA
JA
0,05009 kg m 2
= 2π
= 2π
mgd
mgL
(0.2 kg)⋅ (9,81 m s −1 )⋅ (0,5 m) 2 ,
= 1,42 s
dabei ist d = L = AS Sch der Abstand des Massenmittelpunkts der Scheibe vom
Drehpunkt A .
Anmerkung
Hinweis: Diese Rechnung gaukelt eine vorgespielte Genauigkeit vor, denn die
physikalischen Größen sind jeweils nur auf eine gültige Ziffer angegeben. Damit soll
aber gezeigt werden, dass der Hauptbeitrag von der Verschiebung des
Massenmittelpunkts der Scheibe gegen den Aufhängepunkt, also dem STEINERschen
Beitrag, herrührt. Ohne Berücksichtigung der Massenverteilung der Stange ist in sehr
guter Näherung
J A ≈ mSch L2
das ist aber das Massenträgheitsmoment eines materiellen Punktes (Masse mSch )
im Abstand L von der Drehachse. Das Schwingungsverhalten der Scheibe alleine,
Schwingungslehre
-3-
Prüfungsaufgabe 08
ohne Berücksichtung der Stange, kann näherungsweise als das eines
mathematischen Pendels beschrieben werden.
Die Modellvorstellungen für ein mathematisches Pendel sind
•
ein materieller Punkt (Massenpunkt)
• ’befestigt’ am Ende eines starren, nicht dehnbaren und masselosen Drahts.
Für ein mathematisches Pendel ist die Schwingungsdauer gegeben durch
T0math = 2 π
0,5 m
L
= 2π
g
9,81 m s −1
= 1,42 s
Es bestätigt sich, dass in diesem Fall die Scheibe (ohne Berücksichtigung der
Massenverteilung des Stabs) mit sehr guter Näherung als mathematisches Pendel
betrachtet werden kann.
(b) Um die Schwingungsdauer des Gesamtsystems aus Scheibe und Stab
berechnen zu können, benötigt man den Abstand y S des gemeinsamen
Schwerpunkts vom Drehpunkt A und das neue Massenträgheitsmoment J A∗ .
Aus Symmetriegründen liegt der
Massenmittelpunkt der Stange in der
Stangenmitte.
A
0
•
L
yS
Sst
Die Koordinate y S des Massenmittelpunkts
berechnet sich folgendermaßen
(eindimensionale Anordnung)
•S
• Ssch
yS =
∑ mi ⋅ y i
i
∑ mi
L
+ msch L
2
=
mst + msch
mst
i
y
=
Das Massenträgheitsmoment J A∗ für
die Anordnung aus Scheibe und
Stab ist nach STEINER
(0,3 kg)(
0,5 m
) + (0,2 kg)(0,5 m)
2
0,2 kg + 0,3 kg
= 0,35 m
J A∗ = J st ( A ) + J sch ( A ) = J st ( A ) + J sch (S) + msch L2 ≈ J st ( A ) + msch L2
Schwingungslehre
-4-
Prüfungsaufgabe 08
Massenträgheitsmoment der Stange bezüglich des Drehpunkts A
L
1
L
1
1
J st ( A ) = J st (S ) + mst ( ) 2 =
mst L2 + mst ( ) 2 = mst L2 = (0,3 kg)(0,5 m) 2
2
12
2
3
3
= 0,0250 kg m 2
Mit dem Massenträgheitsmoment der Scheibe J A ( A ) ≈ 0,0500 kg m 2 aus
Teilaufgabe (a) folgt
J A∗ = 0,0250 kg m 2 + 0,0500 kg m 2 = 0,0750 kg m 2 .
Für ein physikalisches Pendel (Scheibe und Stab) ergibt sich die Schwingungsdauer
T0b = 2π
J A∗
0,0750 kg m 2
= 2π
m g yS
(0,2 kg + 0,3 kg) ⋅(9,81 m s − 2 ) ⋅ (0,35 m)
= 1,32 s
dabei ist d = y S = AS der Abstand des gemeinsamen Massenmittelpunkts S von
Scheibe und Stab vom Drehpunkt A .
(c) Die Abweichung der in den Teilaufgaben (a) und (b) in den beiden
Modellrechnungen bestimmten Schwingungsdauern T0a und T0b beträgt
ΔT T0b − T0a 1,42 s − 1,32 s
=
=
T0b
T0b
1,32 s
= 0,076
Dies entspricht einer Abweichung von 7,6 % .
Schwingungslehre
-5-
Prüfungsaufgabe 08
Schwingungslehre – Prüfungsaufgabe 09
Diese Aufgabe wurde in Zusammenhang mit Laborübungen gestellt. Im Labor spielt
die ’Fehlerrechnung’ eine wichtige Rolle.
Ein physikalisches Pendel besteht aus einer schweren Scheibe, die in der Mitte einer
dünnen, massiven, im Punkt D drehbar gelagerten Stange befestigt ist (vgl. Skizze).
Das Pendel befindet sich am Ort der Norm-Schwerebeschleunigung
[ g = 9,806 m s −2 ].
Hinweis: Rechnen sie bitte durchweg mit vier gültigen Ziffern.
D
Scheibe
Masse mSch = 5,000 kg
Radius
L
mSch
r = 0,1500 m
Stange
Masse mSt = 1,300 kg
r
Länge
L = 1,000 m
mSt
Das Pendel wird zu Schwingungen mit kleiner Amplitude angeregt. Berechnen Sie
die Eigenschwingungsdauer T0 für ungedämpfte Schwingungen des physikalischen
Pendels.
(a) Sie wollen Ihr Rechenergebnis überprüfen und messen die Schwingungsdauer
insgesamt zehn mal für jeweils zehn Schwingungen mit folgenden Ergebnissen:
10 T0
s
14,90 15,00 14,80 15,10 15,00 14,80 14,90 15,10 14,90 15,00
Berechnen Sie aus Ihren zehn Messergebnissen den ’Bestwert’ T1 für die Schwingungsdauer. Wie groß ist der Unterschied ΔT = T0 − T1 zwischen dem berechneten
Wert T0 und dem experimentell bestimmten Bestwert T1 ?
(b) Der Grund für die Differenz der beiden Schwingungsdauern könnte in der Dämpfung des Systems liegen. Berechnen sie unter dieser Annahme aus dem Verhältnis T0 /T1 den Dämpfungsgrad D der Schwingungen.
(c) Auf welchen Bruchteil nehmen die Ausschläge in einer Schwingungsperiode ab?
Schwingungslehre
-1-
Prüfungsaufgabe 09
Schwingungslehre – Prüfungsaufgabe 09 – Kurzlösungen
(a) Gesamtmasse des Pendels m = 6,300 k g .
Abstand Drehpunkt-Massenmittelpunkt d = 0,500 m .
Massenträgheitsmoment (STEINER) J D = 1,740 kg m 2 .
Schwingungsdauer T0 = 1,4915 s .
(b) Arithmetischer Mittelwert T1 = 1,495 s .
Dämpfungsgrad D = 0,0731.
(c) Rückgang der Auslenkungen
Schwingungslehre
y1
2
= 0,6317 ; (auf etwa
der Anfangsauslenkung).
y0
3
-2-
Prüfungsaufgabe 09
Schwingungslehre – Prüfungsaufgabe 09 – Musterlösung
(a) Für ein physikalisches Pendel ist die Schwingungsdauer bei kleinen Auslenkungen aus der Ruhelage gegeben durch
T0phys = 2π
JD
mg d
mit m Gesamtmasse
g Schwerebeschleunigung
d Abstand Drehpunkt D – Massenmittelpunkt S
J D Massenträgheitsmoment bezüglich des Drehpunkts D
Die Gesamtmasse des Pendels ist
m = mS ch + mSt = (5,0 + 1,3) kg
= 6,300 kg
Der Abstand d zwischen Drehpunkt D und Massenmittelpunkt S ist aus Symmetriegründen
L 1,00 m
=
2
2
= 0,500 m
d =
Das Massenträgheitsmoment J D bezüglich des Drehpunkts D unter Anwendung des
STEINERschen Satzes
⎛L⎞
J DSch = J SSch + m Sch ⎜ ⎟
2
⎝2⎠
also
J D = JDSt + JDSch =
=(
1
⋅1,300 ⋅12
12
1
1
L
mSt L2 + mSch R 2 + (mSt + mSch )( )2
12
2
2
1
+ ⋅5,000 ⋅0,1500 2 + 6,300⋅0,5000 2 ) k g m 2
2
= (0,1083 + 0,0563 + 1,575 ) k g m 2
= 1,740 kg m 2
damit wird die Schwingungsdauer
1,740 k g m 2
T0 = 2π
6,300 k g⋅9,806 m s
−2
⋅0,5000 m
= 2π 0,0563 s 2
= 1,4915 s
(b) Der arithmetische Mittelwert für die zehn Messungen ist für jeweils zehn Schwingungen
10 T1 =
∑ 10 Ti
Schwingungslehre
i
10
= 14,95 s
-3-
Prüfungsaufgabe 09
damit wird der Mittelwert für eine Schwingungsdauer
14,95 s
T1 =
= 1,495 s
10
Die Differenz aus berechnetem Wert und Mittelwert aus den Messungen ist
ΔT = T0 −T1 = (1,491 − 1,495 ) s
= 4 ⋅10 − 3 s
(c) Die Kreisfrequenz ω d bei viskoser Dämpfung hängt ab von
der Eigenkreisfrequenz ω 0 ,
•
• dem Dämpfungsgrad D.
Es gilt dabei der Zusammenhang
ω d = ω0 1 − D 2
wegen
2π
T
wird daraus die Beziehung für die Schwingungsdauern
ω =
T0
=
T1
1 − D 2 oder
D2 = 1 − (
T0 2
) = 1 − 0,9947 = 0,0053
T1
und
D = 0,0731
Die Schwingungen eines viskos gedämpften Feder-Masse-Systems lassen sich darstellen als
y = yˆ 0 ⋅ e −δ t cos( ωdt + ϕ 0 )
oder
y = yˆ 0 ⋅ e −δ t sin( ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende Exponentialfunktion zu untersuchen; also den Zeitverlauf von
y einh = yˆ 0 e −δt
für zwei Ausschläge im zeitlichen Abstand einer Schwingungsperiode gilt
y 0 = yˆ 0 e −δt
y 1 = yˆ 0 e − δ(t +Td ) = yˆ 0 e − δt e − δTd
Damit wird das Verhältnis der Auslenkungen y 1 und y 0 im Abstand einer Schwingungsperiode Td
y 1 yˆ 0 e − δt e − δTd
=
= e − δTd
−
δ
t
y0
yˆ 0 e
Schwingungslehre
-4-
Prüfungsaufgabe 09
Für den Dämpfungsgrad gilt die Beziehung
δ
D=
ω0
daraus wird der Dämpfungskoeffizient
2π
δ = D ω0 = D
T0
und
δ Td = D
2π
Td
T0
Der in Teilaufgabe (b) berechnete Dämpfungsgrad D = 0,0731 bedeutet wegen
0 < D ≤ 0,1 ’schwache Dämpfung’. Für schwache Dämpfung gilt
Td ≈ T0
Mit dieser Näherung wird das Verhältnis der Auslenkungen im Abstand einer Schwingungsperiode
y1
= e − δ Td = e − 2π D = e − 2π ⋅0,0731 = e −0,4593
y0
= 0,6317
d. h. die Auslenkungen gehen in einer Schwingungsperiode auf etwa
2
der jeweili3
gen Anfangsauslenkung zurück.
Schwingungslehre
-5-
Prüfungsaufgabe 09
Schwingungslehre – Prüfungsaufgabe 10
D
Eine massive Vollkugel aus Aluminium hängt an einem
dünnen Stahldraht. Die Kugel kann
L
•
Pendelschwingungen um den Aufhängepunkt D ,
•
Drehschwingungen um die Achse D − S durch
den Schwerpunkt S
ausführen.
Man beobachtet, dass die Schwingungsdauern T0 ungedämpfter Schwingungen für beide Schwingungsarten
gleich sind.
S
R
(a) Berechnen Sie die Schwingungsdauer T0 für die ungedämpfte Pendelbewegung
bei kleinen Amplituden
(1) in der Näherung als mathematisches Pendel (T0math ) und
(2) als physikalisches Pendel (T0phys ) . Die Masse des Drahtes soll dabei vernachlässigt werden können.
(b) Bestimmen Sie die Drehfederkonstante c * für die Verdrillung (Torsion) des
Drahts. Benutzen Sie dazu die Schwingungsdauer (T0phys ) aus Teilaufgabe (a).
(c) Der Luftwiderstand für die Pendelschwingungen in Teilaufgabe (a) ist zwar sehr
klein; man beobachtet aber, dass in jeweils 15 Schwingungsperioden die Auslen7
ihres Anfangswertes abnehmen.
kungen auf
10
Berechnen Sie daraus den Abklingkoeffizienten δ .
(d) Bei laminarer Strömung ist der Luftwiderstand der Kugel proportional zur Geschwindigkeit und der Bewegung entgegengerichtet; also Freib = − b v .
Bestimmen Sie unter dieser Annahme den Reibungskoeffizienten b des Reibungsgesetzes?
Geometrie und Daten für die Aluminium-Kugel:
Länge des Drahtes
L = 0,25 m ,
Radius der Kugel
R = 0,07 m ,
Dichte
ρ = 2,70 ⋅ 10 3 kg m −3 .
Schwingungslehre
-1-
Prüfungsaufgabe 10
Schwingungslehre – Prüfungsaufgabe 10 – Kurzlösungen
(a) Schwingungsdauer mathematisches Pendel T0math = 1,135 s .
Schwingungsdauer physikalisches Pendels T0phys = 1,146 s .
Masse Aluminiumkugel m = 3,88 kg .
Massenträgheitsmomente J S = 7,60 ⋅ 10 −3 kg m 2 ; JD = 0,405 kg m 2 .
(b) Eigenkreisfrequenz ω0 = 2π ⋅
1
T0phys
.
Drehfederkonstante c * = 0,229 N m .
(c) Abklingkoeffizient δ = 2,08 ⋅ 10 −2 s −1 .
Dämpfungsgrad D = 3,8 ⋅ 10 −3 .
(d) Reibungskoeffizient b =
Schwingungslehre
2 δ JD
LS 2
= 0,164 kgs
-2-
−1
b LS 2
; Abklingkoeffizient δ =
.
2J D
Prüfungsaufgabe 10
Schwingungslehre – Prüfungsaufgabe 10 – Musterlösung
(a) Definition eines mathematischen Pendels:
•
ein Körper der Masse m – behandelt als materieller Punkt
• an einem starren, nicht dehnbaren masselosen Faden der Länge L
In der Näherung 'mathematisches Pendel' gilt für die Schwingungsdauer – beschränkt auf kleine Auslenkungen aus der Ruhelage (Linearisierung) –
T0math = 2π
T0math = 2π
LS
g
dabei ist
LS = (L + R ) = 0,32 m
0,32 m
9,81 m s − 2
= 1,135 s
In der Näherung 'physikalisches Pendel' gilt für die Schwingungsdauer – wieder beschränkt auf kleine Auslenkungen aus der Ruhelage –
T0phys = 2π
JD
m g LS
Dabei ist
m Gesamtmasse
g Schwerebeschleunigung
d Abstand zwischen Drehpunkt D und Massenmittelpunkt S
J D Massenträgheitsmoment bezüglich des Drehpunkts D
Das Massenträgheitsmoment J D bezüglich des Drehpunkts D ergibt sich nach
STEINER zu
2
2
J D = m R 2 + m LS 2 = m ⋅ ( R 2 + LS 2 )
5
5
Zahlenwerte (obwohl man diese explizit erst in den Teilaufgaben (b) und (c) braucht):
Die Masse der Aluminiumkugel ergibt sich aus Dichte ρ und Kugelvolumen V zu
4
4
π R 3 = 2,70 ⋅ 10 3 kg m − 3 ⋅ π ⋅ (7,0 ⋅ 10 − 2 m)3
3
3
= 3,88 kg
m = ρ⋅
damit werden die beiden Massenträgheitsmomente J S und J D
JS =
2
m R 2 = 0,40 ⋅ 3,88 kg ⋅ (7,0 ⋅ 10 − 2 m) 2
5
= 7,60 ⋅ 10 − 3 kg m 2
und
J D = 7,60 ⋅ 10 −3 kg m 2 + 3,88 kg ⋅ 0,32 2 m 2
= 0,405 kg m 2
Schwingungslehre
-3-
Prüfungsaufgabe 10
Die Schwingungsdauer des physikalischen Pendels ergibt sich zu
m[( 2 / 5)R 2 + LS 2 ]
L
LS
2 R2
2 R2
= 2π ⋅ S (1 +
)
=
2
π
⋅
⋅
(
1
+
)
5 LS 2
5 LS 2
m g LS
g
g
T0phys = 2π ⋅
= T0math (1 +
2 R2
2 (7 ⋅ 10 − 2 m) 2
) = 1,135 s ⋅ 1,019
)
=
1
,
135
s
⋅
(
1
+
5 (3,2 ⋅ 10 −1 m) 2
5 LS 2
= 1,146 s
Die Masse der Aluminium-Kugel kürzt sich heraus, die Zahlenwerte der Massenträgheitsmomente braucht man nicht explizit, die vorgegeben Geometrie-Daten sind ausreichend für die Bestimmung der Schwingungsdauer T0phys .
(b) Bei einer linearen Abhängigkeit des rücktreibenden Drehmoments M Rück vom
Verdrillungswinkel ϕ gilt mit der Drehfederkonstante c * als Proportionalitätskonstante
M Rück = − c * ϕ
M Rück ist das einzige auftretende Rückstellmoment; zusammen mit dem Massen-
trägheitsmoment J D des Körpers bezüglich der Drehachse ergibt das NEWTONsche
Grundgesetz für Rotationen
&&
M ges = M Rück = J D ϕ
Daraus erhält man allgemein die Differentialgleichung einer ungedämpften Drehschwingung
&&
− c * ϕ = JK ϕ
&& +
ϕ
c*
ϕ=0
JD
Durch Koeffizientenvergleich mit der Standard-Differentialgleichung
&& + ω0 2 ϕ = 0
ϕ
erhält man für das Quadrat der Eigenkreisfrequenz
c*
ω0 2 =
JD
Mit dem Ergebnis aus Teilaufgabe (a) bestimmt sich die Eigenkreisfrequenz zu
ω 0 = 2π ⋅
1
T0phys
Damit erhält man für die Drehfederkonstante
4 π2
2
4 π2
c * = ( m R 2 ) ( phys ) = 7,60 ⋅ 10 − 3 kg m 2 ⋅
5
(1,146 s) 2
(T
)2
0
= 0,229 N m
Schwingungslehre
-4-
Prüfungsaufgabe 10
(c) Die Schwingungen eines viskos gedämpften Systems lassen sich darstellen als
ϕ = ϕmax ⋅ e −δ t cos( ωdt + ϕ 0 )
oder
ϕ = ϕmax ⋅ e −δ t sin( ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende Exponentialfunktion zu untersuchen; also den Zeitverlauf von
ϕ einh = ϕmax e −δt
oder
ϕ einh
= e − δt
ϕmax
Logarithmieren liefert
⎛ϕ
⎞
ln⎜⎜ einh ⎟⎟ = − δ t
⎝ ϕmax ⎠
Nach n = 15 Schwingungsperioden, also für den Zeitpunkt t = 15 ⋅ T0phys , beobachtet
man
ϕ einh (15 ⋅ T0phys ) = 0,7 ϕmax
also gilt
⎛ 0,7 ⋅ ϕmax
ln ⎜⎜
⎝ ϕmax
⎞
⎟⎟ = − (δ ⋅ 15 ⋅ 1,146 s)
⎠
und
δ=
− 0,357
ln(0,7)
=
= 2,08 ⋅ 10 − 2 s −1
( − 15 ⋅ 1,146 s) ( − 15 ⋅ 1,146 s)
Dabei wurde für einen Dämpfungsgrad D < 0,1 die Näherung Tdphys ≈ T0phys benutzt.
Diese Näherung kann nun überprüft werden. Es ist
phys
D=
T
δ
1,146 s
=δ 0
= 2,08 ⋅ 10 − 2 s −1 ⋅
= 3,8 ⋅ 10 − 3
ω0
2π
2π
Damit ist die benutzte Näherung gerechtfertigt.
(d) Das Reibungsmoment M reib bringt in die Differentialgleichung einen Term ein,
der proportional zur (Geschwindigkeit bzw.) Winkelgeschwindigkeit ist. Der Betrag
des Reibungsmoments ist:
M reib = Freib LS = (b v ) LS = b (LS ϕ& ) LS
Denn die Verknüpfung zwischen der linearen Geschwindigkeit v der Kugel auf einer
Kreisbahn vom Radius LS und der zugehörigen Winkelgeschwindigkeit ω ist gegeben durch
v = LS ω = LS ϕ&
Damit ergibt sich für die Differentialgleichung der gedämpften Schwingung – wieder
beschränkt auf kleine Auslenkungen aus der Ruhelage –
Schwingungslehre
-5-
Prüfungsaufgabe 10
&& + b LS 2 ϕ& + m g LS ϕ = 0
JD ϕ
&& +
ϕ
b LS 2
m g LS
ϕ& +
ϕ=0
JD
JD
Methodentransfer aus der Standard-Differentialgleichung für das Feder-MasseSystem mit Dämpfung
y&& + 2 δ y& + ω0 2 y = 0
liefert die Eigenkreisfrequenz
ω0 2 =
m g LS
JD
(vgl. auch Teilaufgabe (a))
und den Zusammenhang zwischen Reibungskoeffizient b und Abklingkonstante δ
δ=
b LS 2
2 JD
also
b=
2 δ JD
LS 2
Mit den Zahlenwerten für J D aus Teilaufgabe (a) erhält man für den Dämpfungskoeffizienten
b=
2 ⋅ 0,0207 s −1 ⋅ 0,405 kg m 2
0,32 2 m 2
= 0,164 kg s −1
Schwingungslehre
-6-
Prüfungsaufgabe 10
Schwingungslehre – Prüfungsaufgabe 11
Ein physikalisches Pendel besteht aus zwei gleichen, schweren Kugeln (Radius r),
die auf einen dünnen Stab gesteckt sind, der durch die Zentren der beiden Kugeln
geht (vgl. Skizze). Die Masse des Stabes sei vernachlässigbar. Das Pendel ist im
Punkt D drehbar gelagert.
Angaben zur Geometrie:
L1 = 0,3 m
L2 = 0,2 m
L2
D
r = 0,1 m
r
g
L1
r
(a) Berechnen Sie die Schwingungsdauer T0 für freie, ungedämpfte Schwingungen
bei kleinen Auslenkungen aus der Ruhelage.
Die Bewegung des Pendels ist durch eine schwache, geschwindigkeitsproportionale
Reibungskraft gedämpft. Man beobachtet, dass die Winkelauslenkungen nach
jeweils fünf Schwingungsperioden auf die Hälfte abnehmen.
(b) Berechnen Sie die Abklingkonstante δ und den Dämpfungsgrad D für diese
gedämpften Schwingungen.
(c) Auf welchen Bruchteil p der Anfangsauslenkung ist die Auslenkung nach
insgesamt n = 20 Schwingungen zurückgegangen?
Schwingungslehre
-1-
Prüfungsaufgabe 11
Schwingungslehre – Prüfungsaufgabe 11 – Kurzlösungen
(a) Abstand Drehpunktes D Massenmittelpunkt S d = 0,05 m .
&& + 2 m g d β = 0 .
Differentialgleichung (linearisiert) β
JD
Massenträgheitsmoment (mit STEINER) J D = J D1 + JD2 = m ⋅ 13,8 ⋅ 10 −2 m 2 .
Schwingungsdauer T0 = 2π
JD
= 2,36 s .
2mgd
(b) Abklingkoeffizient δ = 5,87 ⋅ 10 −2 s −1;
Dämpfungsgrad D = 2,20 ⋅ 10 −2 < 0,1 (schwache Dämpfung).
4
(c) Bruchteil p =
Schwingungslehre
1 1 1 1 ⎛ 1⎞
1
⋅ ⋅ ⋅ =⎜ ⎟ =
.
2 2 2 2 ⎝2⎠
16
-2-
Prüfungsaufgabe 11
Schwingungslehre – Prüfungsaufgabe 11 – Musterlösung
(a) Der Massenmittelpunkt S des physischen Pendels liegt aus Symmetriegründen
(identische Kugeln) und der Idealisierung eines 'masselosen' Stabs genau in der
Mitte zwischen den beiden Kugelmittelpunkten, also jeweils 0,25 m von den
Kugelmittelpunkten entfernt. Damit wird der Abstand d zwischen dem
Massenmittelpunkt S des Pendels und dem Drehpunkt D
d = 0,05 m unterhalb des Drehpunktes D
Das gleiche Ergebnis liefert die sture Berechnung des Massenmittelpunktes nach
seiner Definition
yS =
∑ mi ⋅ y i
∑ mi
=
m ⋅ 0 + m ⋅ (L1 + L2 ) (L1 + L2 )
=
= 0,25 m
2
m+m
dabei ist es unerheblich, in welchen Massenmittelpunkt der Nullpunkt des
Koordinatensystems gelegt wird. Außerdem müssen die Massen der beiden Kugeln
gar nicht explizit bekannt sein.
Bei einer Auslenkung aus der Ruhelage wird der Betrag des rücktreibenden
Drehmoments
M Rück = − ( m ges ) g d sin β = − ( 2 m ) g d sin β ≅ − 2 m g d β
Bei der Berechnung des Drehmoments wird die Gesamtmasse des Pendels als im
Massenmittelpunkt vereinigt angenommen.
Die Linearisierung sin β ≅ β gilt für die Näherung ’kleiner Auslenkungen’, also β << 1 .
Die Grundgleichung für Drehbewegungen nach NEWTON lautet
M Rück = J D
d 2β
dt
2
&&
= JD β
also
&&
− 2 m g d β = JD β
Damit ergibt sich für die Schwingung die Differentialgleichung
&& + 2 m g d β = 0
β
JD
Koeffizientenvergleich mit der Standard-Differentialgleichung für harmonische
Schwingungen
y&& + ω0 2 y = 0
liefert als Beziehung für die Eigenkreisfrequenz
2mgd
ω0 2 =
JD
Daraus ergibt sich die Schwingungsdauer des physikalischen Pendels – mit der
Einschränkung ’kleine Auslenkungen’ aus der Ruhelage –
T0 =
JD
2π
= 2π
2m g d
ω0
Schwingungslehre
-3-
Prüfungsaufgabe 11
Die Beziehung für das Massenträgheitsmoment J D im Zähler dieser Gleichung
enthält die Masse m ; die sich gegen die Masse m im Nenner herauskürzt. Die
Masse m braucht also explizit gar nicht bekannt zu sein.
Das Massenträgheitsmoment J D bezüglich des Drehpunkts D ergibt sich als
Summe aus den beiden Massenträgheitsmomenten J D1 und JD2 der beiden Kugeln
bezüglich des Drehpunkts D . Berücksichtigung des STEINERschen Satzes liefert
2
m r 2 + m L12
5
2
= m r 2 + m L2 2
5
J D1 =
J D2
also
2
2
J D = J D1 + J D2 = ( m r 2 + m L12 ) + ( m r 2 + m L2 2 )
5
5
4
= m ( r 2 + L12 + L2 2 ) = m ⋅ (0,8 ⋅ 10 − 2 m 2 + 9 ⋅ 10 − 2 m 2 + 4 ⋅ 10 − 2 m 2 )
5
= m ⋅ 13,8 ⋅ 10 − 2 m 2
Damit wird die Schwingungsdauer T0 [die Masse m in Zähler und Nenner kürzt sich
heraus, braucht also explizit gar nicht bekannt zu sein].
T0 = 2π
JD
m ⋅ 13,8 ⋅ 10 − 2 m − 2
= 2π
2mgd
2 ⋅ m ⋅ 9,81 m s − 2 ⋅ 0,05 m
= 2,36 s
(b) Die Schwingungen eines viskos gedämpften Systems lassen sich darstellen als
ϕ = ϕmax ⋅ e −δ t cos( ωdt + ϕ 0 ) oder
ϕ = ϕmax ⋅ e −δ t sin( ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende
Exponentialfunktion zu untersuchen; also den Zeitverlauf von
ϕ einh = ϕmax e −δt
oder
ϕ einh
= e−δ t
ϕmax
Logarithmieren liefert
⎛ϕ
⎞
ln ⎜⎜ einh ⎟⎟ = − δ t
⎝ ϕmax ⎠
bei schwacher Dämpfung ist Td ≅ T0 (diese Annahme muss am Ende überprüft
werden) und man erhält für fünf Schwingungsperioden eine Abnahme der
Auslenkungen auf die Hälfte, also
Schwingungslehre
-4-
Prüfungsaufgabe 11
⎛1
⎜ ϕmax
ln⎜ 2
⎜ ϕmax
⎜
⎝
also
⎞
⎟
⎟ = − δ ⋅ 5T0
⎟
⎟
⎠
⎛ 1⎞
ln ⎜ ⎟ = − δ ⋅ 5T0
⎝2⎠
ln1 − ln 2 = −δ ⋅ 5T0
da ln1 = 0
wird
ln 2
ln 2
=
5T0 5 ⋅ 2,36 s
δ=
= 5,87 ⋅ 10 − 2 s −1
Daraus erhält man den Dämpfungsgrad
D=
δT
δ
= 0 = 2,20 ⋅ 10 − 2 < 0,1
2π
ω0
Damit ist die oben gemachte Annahme 'schwache Dämpfung' bestätigt.
(c) Für den Bruchteil, auf den die Anfangsauslenkung nach n = 20 Schwingungen
zurückgegangen ist, gilt mit Td ≅ T0
⎛ϕ
ln( p) = ln⎜⎜ einh
⎝ ϕmax
⎞
⎟⎟ = − δ (20 ⋅ Td ) ≅ 4 ( − δ ⋅ 5T0 )
⎠
mit dem Ergebnis aus Teilaufgabe (b1)
δ (5T0 ) = ln 2
geht das ohne Zahlenwerte und Taschenrechner
ln( p ) = − 4 ⋅ ln 2 = ln(2 −4 )
p = 2− 4
p=
1
16
Argumentation ganz ohne Rechnung:
In jeweils fünf Schwingungsperioden geht die Auslenkung auf die Hälfte zurück. Also
in vier dieser (willkürlichen) Zeiteinheiten vier Mal auf jeweils die Hälfte; der Bruchteil
wird
4
1 1 1 1 ⎛ 1⎞
1
p= ⋅ ⋅ ⋅ =⎜ ⎟ =
2 2 2 2 ⎝2⎠
16
Schwingungslehre
-5-
Prüfungsaufgabe 11
Schwingungslehre – Prüfungsaufgabe 12
Ein quadratischer Rahmen besteht aus vier dünnen Stäben
der Länge L . Der Rahmen wird an einer Ecke A drehbar
aufgehängt. Der Rahmen wird in der Zeichenebene aus der
Ruhelage ausgelenkt und schwingt anschießend frei in
dieser Ebene mit der Schwingungsdauer T0 = 2,00 s .
A
L
L
(a) Berechnen Sie die Länge L eines Stabes unter
L
L
Vernachlässigung von Reibungseinflüssen und unter
Beschränkung auf kleine Ausschläge der
Schwingungsbewegung.
Durch einen Defekt im Lager wird die Schwingung gedämpft. Das Reibungsmoment
ist proportional zur Winkelgeschwindigkeit des Rahmens. Infolge dieser Dämpfung
vergrößert sich die Schwingungsdauer des Rahmens um 1 %.
(b) Bestimmen Sie den Dämpfungsgrad D und den Abklingkoeffizienten δ der
gedämpften Schwingung.
(c) Welchen Betrag hat die Auslenkung nach insgesamt drei Schwingungen, wenn
sie zu Beginn βˆ 0 = 6 o war?
Hinweis: Das Massenträgheitsmoment eines dünnen Stabes (Masse m , Länge L )
bezüglich einer Achse, die senkrecht zur Stabachse durch den Schwerpunkt geht,
1
beträgt J S =
mL2 .
12
Schwingungslehre
-1-
Prüfungsaufgabe 12
Schwingungslehre – Prüfungsaufgabe 12 – Kurzlösungen
10
(a) Massenträgheitsmoment Rahmen J A =
mStab L2 .
3
Gesamtmasse Rahmen m = 4 mStab .
Stablänge L =
3 2 T0 2 g
20 π 2
= 0,843 m .
(b) Schwingungsdauer Td = 1,01⋅ T0 = 2,02 s .
Verhältnis der Kreisfrequenzen
ωd
1
=
= 0,990 .
ω0 1,01
Dämpfungsgrad D = 0,141.
Abklingkoeffizient δ = D ω0 = 0,443 s −1 .
(c) Winkelauslenkung β (3Td ) = 6 o ⋅ 0,069 = 0,42 o .
Schwingungslehre
-2-
Prüfungsaufgabe 12
Schwingungslehre – Prüfungsaufgabe 12 – Musterlösung
(a) Für ein physikalisches Pendel gilt für ’kleine Auslenkungen’ aus der Ruhelage für
die Schwingungsdauer
T0phys = 2π
JA
mgd
Mit
J A Massenträgheitsmoment bezüglich einer Drehachse durch A
m Gesamtmasse des Rahmens
g Erdbeschleunigung
d Abstand ( AS ) zwischen Drehpunkt A und Gesamtmassenmittelpunkt S
Kleine Auslenkungen sind die einschränkende Bedingung, um die
Differentialgleichung zu linearisieren (also die Näherung sin β ≈ β für β << 1 ).
Das Massenträgheitsmoment J A setzt sich additiv aus den Einzelbeiträgen J i der
vier Rahmenstäbe zusammen. Da die Drehachse für keine der vier Stäbe durch den
jeweiligen Massenmittelpunkt eines Einzelstabs geht, ist zur Berechnung der
Massenträgheitsmomente jeweils der STEINERsche Satz anzuwenden.
A
A
L
2
L
2
L
2
Für die beiden oberen Stäbe ist der Abstand zwischen Drehpunkt A und den
Massenmittelpunkten der beiden Stäbe S St
L
2
Für die beiden unteren Stäbe ist der Abstand zwischen Drehpunkt A und ihren
Massenmittelpunkten S St aus einem rechtwinkligen Dreieck nach PYTHAGORAS zu
bestimmen; er ergibt sich zu
a1 =
L
5
a2 2 = L2 + ( ) 2 = L2
4
2
Bei der Anwendung des STEINERschen Satzes geht nur das Quadrat der
Verschiebung ein.
Schwingungslehre
-3-
Prüfungsaufgabe 12
Es werden damit
J A1 = 2 ⋅ mStab ⋅ (
1 2 L2 3
2
L +
⋅ ) = mStab L2
12
4 3
3
J A 2 = 2 ⋅ mStab ⋅ (
1 2 5 2 3
2 ⋅ 16
8
L + L ⋅ )=
mStab ⋅ L2 = mStab L2
12
4
3
12
3
Das gesamte Massenträgheitsmoment des Rahmens wird
J A = J A1 + J A 2 =
2
8
mStab L2 + mStab L2
3
3
10
mStab L2
3
Die Gesamtmasse des Rahmens erhält man durch Addition der Einzelmassen
=
m = 4 mStab
Der Massenmittelpunkt S eines quadratischen Rahmens liegt aus Symmetriegründen
im Zentrum des Quadrats. Der Abstand zwischen Drehpunkt A und
Massenmittelpunkt S ist damit gleich der halben Diagonale des Quadrats, also
2
L
2
Diese Werte eingesetzt in die (quadrierte) Gleichung für die Schwingungsdauer
ergibt
d=
10
) mStab L2
10 ⋅ L ⋅ 2 20 π 2 L
3
T0 2
= π2
=
2
3g 2 3 2 g
4 mStab g (
)L
2
Daraus ergibt sich die Stablänge L zu
J
= ( 2π ) 2 A = 4 π 2
mgd
L=
3 2 T0 2 g
20 π 2
=
(
3 2 ⋅ (2,00 s) 2 ⋅ 9,81 m s −2
20 π 2
= 0,843 m
(b) Die Schwingungsdauer Td bei Vorliegen von Dämpfung ist um 1 % größer als
T0 ; also gilt
Td = 1,01⋅ T0 = 1,01⋅ 2,00 s = 2,02 s
Mit
ω 0 = 2π ⋅
Schwingungslehre
1
T0
und
ω d = 2π ⋅
1
Td
-4-
Prüfungsaufgabe 12
wird das Verhältnis der Kreisfrequenzen
ωd 2π T0 T0
T0
1
=
⋅
=
=
=
= 0,990
ω0 Td 2π Td 1,01⋅ T0 1,01
Der Zusammenhang zwischen ω d und ω0 wird bestimmt vom Dämpfungsgrad D ,
gemäß
ωd 2 = ω0 2 (1 − D 2 )
Damit
D2 = 1 − (
ωd 2
ω0
2
) = 1 − (0,990 ) 2 = 0,020
D = 0,141
Abklingkoeffizient δ , Dämpfungsgrad D und Eigenkreisfrequenz ω0 sind verknüpft
gemäß
δ = D ω0 = D
2π
2π
= 0,141⋅
T0
2,00 s
= 0,443 s −1
(c) Das Abklingen der Schwingungsauslenkungen bei viskoser Reibung wird durch
die Einhüllende einer Exponential-Funktion beschrieben; also
β(t ) = βˆ 0 ⋅ e −δt
Damit wird die Winkelauslenkung der Schwingung nach drei Schwingungsperioden,
also t = 3 ⋅ Td = 6,06 s
β (3Td ) = 6 o ⋅ e − (0,443 s
−1
⋅ 3 ⋅ 2,02 s )
= 6 o ⋅ 0,069 = 0,42 o
Schwingungslehre
-5-
Prüfungsaufgabe 12
Schwingungslehre – Prüfungsaufgabe 13
Mit dem POHLschen Drehpendel werden Drehschwingungen untersucht.
In einer ersten Messung wird für insgesamt zehn Schwingungen eines ungedämpften
Systems eine Gesamtzeit t = 22,5 s gemessen.
Um das System viskos zu dämpfen, wird in einem zweiten Versuch eine
Wirbelstrombremse eingeschaltet. Man beobachtet in zehn Schwingungsperioden
eine Abnahme der Auslenkungen (abgelesen auf einem Skalenring) von anfangs 50
Skalenteilen auf 10 Skalenteile.
Bei einer viskos gedämpften Schwingung nehmen die Auslenkungen exponentiell mit
der Zeit ab, gemäß
β(t ) = βˆ 0 ⋅ e −δ ⋅ t
Bestimmen Sie aus diesen Angaben
(a) den Abklingkoeffizienten δ und
(b) den Dämpfungsgrad D des schwingenden Systems.
Schwingungslehre
-1-
Prüfungsaufgabe 13
Schwingungslehre – Prüfungsaufgabe 13 – Kurzlösungen
(a) Abklingkoeffizient δ = 0,0715 s −1 .
(b) Schwingungsdauer T0 = 2,25 s .
Eigenkreisfrequenz ω0 = 2,79 s −1 .
Dämpfungsgrad D = 2,56 ⋅ 10−2 < 0,1 .
Schwingungslehre
-2-
Prüfungsaufgabe 13
Schwingungslehre – Prüfungsaufgabe 13 – Musterlösung
(a) Die Auslenkungen eines viskos gedämpften schwingenden Systems klingen
exponentiell ab; also gilt
β(t ) = βˆ 0 e −δt
oder umgestellt
β(t )
= e−δ t
ˆβ 0
Logarithmieren dieser Beziehung liefert
⎛ β(t ) ⎞
⎟ = ln(e − δt ) = − δ t
ln⎜⎜
⎟
ˆ
⎝ β0 ⎠
Mit der Näherung Td ≈ T0 für Dämpfungsgrade D < 0,10 wird für Z = 10
Schwingungsperioden, also für eine Gesamtzeit von t Z = 10 Td ≈ 10 T0
⎛ β(t = 10 T0 ) ⎞
⎟⎟ = − δ ⋅ 10 T0
ln⎜⎜
⎝ β(t = 0) ⎠
oder
⎛ β(t = 10 T0 ) ⎞
⎟
ln⎜⎜
β(t = 0) ⎟⎠
⎝
δ=−
10 T0
Zahlenwerte
⎛ 10 ⎞
⎛ 10 ⎞
ln⎜ ⎟
ln⎜ ⎟
ln1 − ln5
0 − 1,61
50
50
δ=− ⎝ ⎠ =− ⎝ ⎠ =−
=−
22,5 s
22,5 s
22,5 s
22,5 s
= 0,0715 s −1
(b) Der Dämpfungsgrad D ist definiert als das Verhältnis aus Abklingkoeffizient
δ und Eigenkreisfrequenz ω0
D=
δ
ω0
Die Schwingungsdauer T0 für die ungedämpfte Schwingung ist
t Z 22,5 s
=
Z
10
= 2,25 s
T0 =
daraus bestimmt sich die Eigenkreisfrequenz zu
2π
2π
ω0 =
=
Z
2,25 s
= 2,79 s -1
Schwingungslehre
-3-
Prüfungsaufgabe 13
Der Dämpfungsgrad wird damit
D=
7,15 ⋅ 10 −2 s −1
2,79 s −1
= 2,56 ⋅ 10 − 2
Damit ist die Forderung ’schwache Dämpfung‘ ( 0 < D ≤ 0,10 ) erfüllt und für die
Schwingungsdauern im gedämpften und ungedämpften Fall die benutzte Näherung
Td ≈ T0 erlaubt.
Schwingungslehre
-4-
Prüfungsaufgabe 13
Schwingungslehre – Prüfungsaufgabe 14
In einem Vorversuch wird die Drehfederkonstante einer Torsionsfeder zu
c ∗ = 0,1 N m bestimmt. Die Drehfeder wird mit einem breiten Kupferring samt
Speichen, zu einem POHLschen Drehpendel zusammengebaut.
In einem ersten Versuch wird die Schwingungsdauer dieses Drehpendels ohne
äußere Dämpfung zu T0 = 2,0 s bestimmt.
In einem zweiten Versuch wird das Drehpendel durch eine Wirbelstrombremse
gedämpft. Man beobachtet, dass die Auslenkungen nach jeweils drei Schwingungen
um 10 % zurückgehen.
(a) Berechnen Sie die Abklingkoeffizient δ und den Dämpfungsgrad D der
gedämpften Schwingung.
∗
(b) Welcher Dämpfungskoeffizient bap
bestimmt für dieses System den
aperiodischen Grenzfall?
Schwingungslehre
-1-
Prüfungsaufgabe 14
Schwingungslehre – Prüfungsaufgabe 14 – Kurzlösungen
(a) Abklingkoeffizient δ = 1,76⋅10 −2 s −1 .
Eigenkreisfrequenz ω0 =
2π
= π s −1 .
T0
Dämpfungsgrad D = 5,6 ⋅ 10 −3 < 0,1 (schwache Dämpfung).
∗
(b) Dämpfungskoeffizient bap
= 6,4⋅10 −2 kg m 2 s −1 .
Schwingungslehre
-2-
Prüfungsaufgabe 14
Schwingungslehre – Prüfungsaufgabe 14 – Musterlösung
(a) Bei viskoser Dämpfung durch die Wirbelstrombremse ist die Einhüllkurve einer
abklingenden Drehschwingung eine Exponentialfunktion, gemäß
β(t ) = βˆ 0 e −δt
oder umgestellt
β(t )
= e−δ t
ˆβ 0
Logarithmieren dieser Beziehung liefert
⎛ β(t ) ⎞
⎟ = ln(e − δ t ) = − δ t
ln⎜⎜
⎟
ˆ
⎝ β0 ⎠
Unter der – später zu überprüfenden – Voraussetzung ’schwache Dämpfung’, also
einem Dämpfungsgrad 0 < D ≤ 0,1, darf die Periodendauer der gedämpften
Schwingung gleich der der ungedämpften Schwingung gesetzt werden, also
Td ≈ T0 = 2,0 s
Für den Zeitpunkt t = 3T0 wird für die Auslenkung beobachtet
β(3T0 ) = 0,9 βˆ 0
die oben hergeleitete Beziehung liefert für diese Werte
⎛ β(3 T0 ) ⎞
⎛ 0,9 βˆ 0 ⎞
⎟
⎜
⎟
ln⎜⎜
ln
⎜ βˆ
⎟
ˆ0 ⎟
β
⎠ = − ⎝ 0 ⎠ = − ln(0,9)
δ=− ⎝
3 T0
3 ⋅ 2,0 s
6,0 s
= 1,76⋅10 − 2 s −1
Der Dämpfungsgrad D ist definiert als Quotient aus Abklingkoeffizient δ und
Eigenkreisfrequenz ω0
D=
δ
ω0
Die Eigenkreisfrequenz ω0 bestimmt sich aus der gemessenen Schwingungsdauer
T0 zu
ω0 =
2π
2π
=
T0 2,0 s
= π s −1
Schwingungslehre
-3-
Prüfungsaufgabe 14
Damit wird der Dämpfungsgrad
D=
δ
1,76⋅10 −2 s −1
=
ω0
π s −1
= 5,6 ⋅ 10 − 3
d. h., es liegt (sehr) schwache Dämpfung vor, und damit ist die oben gemachte
Näherung Td ≈ T0 erlaubt.
(b) Der Abklingkoeffizient δ ist darstellbar aus Dämpfungskoeffizient b * und
Massenträgheitsmoment J als
b∗
δ=
2J
[Analogie zum Federpendel mit δ =
b
]
2m
oder umgestellt
b ∗ = 2δ J
Für den aperiodischen Grenzfall ist der Dämpfungsgrad
D =1
also gilt für den aperiodischen Grenzfall
δ = ω0
Damit kann das Massenträgheitsmoment J aus der Eigenkreisfrequenz ω0 und der
Drehfederkonstanten c ∗ berechnet werden. Es gilt für das Quadrat der
Eigenkreisfrequenz
c∗
c
[Analogie zum Federpendel mit ω0 2 = ]
J
m
oder für das Massenträgheitsmoment des Kupferrings mit Speichen
ω0 2 =
J=
c∗
T0 2
ω0
4 π2
= c∗
2
∗
Damit ergibt sich der Dämpfungskoeffizient bap
für den aperiodischen Grenzfall zu
∗
bap
T0 2
c ∗T0
0,1 N m ⋅ 2,0 s
2π
= 2 δ J = 2 ω0 J = 2
c*
=
=
2
T0
π
π
4π
= 6,4 ⋅ 10 − 2 kg m 2 s −1
Schwingungslehre
-4-
Prüfungsaufgabe 14
Schwingungslehre – Prüfungsaufgabe 15
Drei gleiche, dünne Stäbe (Länge
L = 30 cm , Masse m = 0,2 kg ), sind durch
zwei (masselose) Gelenke zu einem
rechtwinkligen U verbunden. Der mittlere
Stab ist in horizontaler Lage in seinem
Schwerpunkt an einem vertikalen elastischen Torsionsdraht aufgehängt; die beiden äußeren Stäbe hängen dabei parallel
zum Torsionsdraht senkrecht nach unten.
Die Gelenke seien zunächst steif.
r
g
L
L
L
(a) Berechnen Sie das Massenträgheitsmoment J1 der Stabanordnung für die mit
dem Draht zusammenfallende Dreh- und Symmetrieachse.
Das Massenträgheitsmoment eines (dünnen) Stabs (Länge L und Masse m )
bzgl. einer zur Stabachse senkrechten Schwerpunktachse ist gegeben durch
1
J st =
mL2 .
12
(b) Das Stab-U wird von Hand aus der Ruhelage insgesamt zwanzig Mal um die vertikale Drahtachse gedreht und dann losgelassen. Es kehrt darauf als Torsionsschwinger in 20 Sekunden zur Ruhelage zurück und setzt anschließend seine
ungedämpften harmonischen Schwingungen fort.
Bestimmen Sie die Kreisfrequenz ω01 dieses Drehpendels.
(c) Berechnen Sie aus den Ergebnissen der Teilaufgaben (a) und (b) die Drehfederkonstante c * des Aufhängedrahts.
(d) Welche Winkelgeschwindigkeit hat die U-Stab-Anordnung beim Durchgang durch
die Ruhelage?
(e) Welche Arbeit WDrill war vor Beginn der Schwingung insgesamt zur Verdrillung
aufzuwenden?
Im Augenblick des 'Nulldurchgangs' – also bei maximaler Winkelgeschwindigkeit –
werden die beiden Gelenke durch ein Steuersignal berührungsfrei aus ihrer Blockierung entriegelt und die zwei freiwerdenden Seitenstäbe (z. B. mit in den Gelenken
eingebauten gespannten Federn) um die beiden Enden des Mittelstabs nach außen
in die Horizontale geschwenkt. Aus der U-Form entsteht so ein gerader Stab. Der
Vorgang läuft in einer, im Vergleich zur Schwingungsdauer, sehr kurzen Zeit ab.
(f) Welches Massenträgheitsmoment J 2 hat diese Anordnung bezüglich der Fadenachse?
(g) Auf welchen Wert ändert sich die maximale Winkelgeschwindigkeit bei Nulldurchgang der Schwingung durch diese geometrische Formänderung?
Schwingungslehre
-1-
Prüfungsaufgabe 15
Schwingungslehre – Prüfungsaufgabe 15 – Kurzlösungen
(a) Massenträgheitsmoment U-Stab J1 = 1,05 ⋅ 10 −2 kg m 2 .
(b) Eigenkreisfrequenz ω01 = 7,9 ⋅ 10 −1 s −1 .
(c) Drehfederkonstante c * = 6,55 ⋅ 10 −5 N m .
(d) Maximale Winkelgeschwindigkeit β& 1max = βˆ 1 ⋅ ω01 = 9,9 s −1 .
(e) Verdrillungsarbeit WDrill = 5,17 ⋅ 10 −1 J .
(f) Massenträgheitsmoment J 2 = 4,05 ⋅ 10 −2 kg m 2 .
(g) Drehimpulserhaltung; Maximale Winkelgeschwindigkeit β& 2 max = 2,57 s −1 .
Schwingungslehre
-2-
Prüfungsaufgabe 15
Schwingungslehre – Prüfungsaufgabe 15 – Musterlösung
(a) Das Massenträgheitsmoment J1 der Stäbe in U-Anordnung setzt sich additiv aus
den Massenträgheitsmomenten der drei einzelnen Stäbe zusammen. Die Einzelbeiträge der drei Stäbe sind
•
Ein horizontaler Stab
J H1 =
1
m L2
12
L
2J V1 = 2 m ( ) 2
2
Bei einem dünnen Stab (Durchmesser << Länge) ist das axiale Massenträgheitsmoment J axial ≈ 0 ; weil die einzelnen Masseteilchen des Stabes für diese Drehachse
sich nur geringfügig außerhalb der Drehachse befinden.
Damit wird das Massenträgheitsmoment für die U-Stab-Anordnung
•
Zwei vertikale Stäbe
J1 = J H1 + 2J V1 = (
1 1 6
7
7
+ ⋅ ) m L2 =
m L2 =
⋅ 0,2 kg ⋅ (0,3 m) 2
12 2 6
12
12
= 1,05 ⋅ 10 − 2 kg m 2
(b) Das Zeitintervall zwischen maximaler Auslenkung (nach zwanzig vollen Umdrehungen) und erstem Durchgang durch die Ruhelage entspricht gerade einem Viertel
T
einer Schwingungsperiode, also Δt = 01 . Dabei ist T01 die Schwingungsdauer der
4
ungedämpften Torsionsschwingung des Systems. Damit erhält man als Eigenkreisfrequenz
ω01 =
2π
2π
2π
=
=
T01 4 Δt 80 s
= 7,9 ⋅ 10 −1 s −1
(c) Die Eigenkreisfrequenz der Torsionsschwingung bestimmt sich eindeutig aus der
Drehfederkonstante c* des Drahts und dem Massenträgheitsmoment J1 der Uförmigen Stabanordnung, gemäß
c
c*
[Analogie zum Federpendel mit ω0 2 = ]
ω012 =
m
J1
oder umgeformt
c * = J1 ⋅ ω012
Mit den Ergebnissen der Teilaufgaben (a) und (b) wird
c * = 1,05 ⋅ 10 −2 kg m 2 ⋅ (7,9 ⋅ 10 −2 s −1 ) 2 = 6,55 ⋅ 10 −5 kg m m s -2
= 6,55 ⋅ 10 − 5 N m
Schwingungslehre
-3-
Prüfungsaufgabe 15
(d) Eine ungedämpfte harmonische Torsionsschwingung wird beschrieben durch
β = βˆ 1 cos(ω01t + ϕ0 )
(Bei der Wahl einer Kosinus-Funktion zur Beschreibung einer harmonischen Schwingung wird wegen der Anfangsbedingung 'Loslassen ohne Anfangswinkelgeschwindigkeit' der Nullphasenwinkel ϕ0 = 0 .)
Die Winkelgeschwindigkeit β& ergibt sich als zeitliche Ableitung der AuslenkwinkelZeit-Funktion allgemein als
β& = − βˆ 1 ω01 sin (ω01t )
Der Betrag ihres Maximalwerts ist der Vorfaktor der Sinusfunktion, denn der Betrag
der Sinus-Funktion ist beschränkt auf den Bereich 0 ≤ sin(ω01t ) ≤ 1; also wird der
Betrag der maximalen Winkelgeschwindigkeit
β& 1max = βˆ 1 ⋅ ω01 = 20 ⋅ 2π ⋅ 7,9 ⋅ 10 −2 s −1
= 9,9 s −1
Alternative: Der erste Nulldurchgang mit dem maximalen Betrag der Winkelgeschwindigkeit wird nach einem Viertel einer Schwingungsperiode erreicht, also zum
T
Zeitpunkt t = 0 . Damit wird das Argument der Sinus-Funktion
4
(ω01t ) =
2π T0 π
⋅
=
T0 4 2
und der zugehörige Wert der Sinus-Funktion
π
sin ( ω01t ) = sin = 1 .
2
Damit ergibt sich wieder das vorige Ergebnis.
Das negative Vorzeichen bedeutet: Bei positiver Anfangsauslenkung ist die Geschwindigkeit beim ersten Nulldurchgang in die negative Koordinatenrichtung gerichtet.
(e) Die aufzuwendende Verdrillungsarbeit ist proportional dem Quadrat des Verdrillungswinkels, gemäß
1
1
(analog zum Federpendel WFeder = c y 2 )
WDrill = c * βDr 2
2
2
mit c * aus Teilaufgabe (c) und dem gesamten Verdrillungswinkel aus 20 vollen Umdrehungen
βDr = (20 ⋅ 2π)
(Winkelangaben immer im Bogenmaß!)
wird
WDrill =
1
⋅ 6,55 ⋅ 10 − 5 N m ⋅ (20 ⋅ 2π) 2
2
= 5,17 ⋅ 10 −1 J
Schwingungslehre
-4-
Prüfungsaufgabe 15
(f) Das Massenträgheitsmoment nach der Entriegelung ist das einer Stange der Gesamtmasse m ges = 3 m und der Gesamtlänge Lges = 3 L für eine Achse durch ihren
Massenmittelpunkt senkrecht zur Stange, also
J2 =
1
27
9
(3 m ) (3 L ) 2 =
m L2 = m L2
12
12
4
= 4,05 ⋅ 10 − 2 kg m 2
(g) Da bei der berührungsfreien Befreiung der Blockierung im Nulldurchgang keine
r
äußeren Drehmomente auf das Torsionspendel wirken, bleibt der Drehimpuls L des
Systems nach Betrag und Richtung erhalten. Es gilt also für die Beträge
r
r
L1max = L2 max
J1 β& 1max = J 2 β& 2 max
oder schließlich
J
1,05 ⋅ 10 −1 kg m 2
β& 2 max = 1 β& 1max =
⋅ 9,9 s −1
2
2
−
J2
4,05 ⋅ 10 kg m
= 2,57 s −1
Schwingungslehre
-5-
Prüfungsaufgabe 15
Schwingungslehre – Prüfungsaufgabe 16
Eine homogene Scheibe (Masse m = 10,0 kg ) wird für zwei
Schwingungsexperimente benutzt. Es soll jeweils Reibungsfreiheit gelten. S ist der
Massenmittelpunkt und P der jeweilige Drehpunkt für die Schwingungen (vgl.
Skizze).
Experiment (A)
Die Scheibe soll in horizontaler Lage
Drehschwingungen um eine Drehachse
senkrecht zur Scheibe durch den Punkt
P ausführen. Das Rückstellmoment
bewirkt eine Spiralfeder (vgl. Skizze).
S
d
P
Ein Vorversuch zur Bestimmung der
Drehfederkonstante c ∗ liefert als
Ergebnis: Eine Verdrillung um den
Winkel β = 45 o erfordert ein äußeres
Drehmoment M = (π / 2) N m .
(a) Bestimmen Sie die Drehfederkonstante c ∗ der Spiralfeder.
(b) Für insgesamt Z = 10 Schwingungen der Scheibe misst man eine Zeit von
t1 = 24,5 s . Bestimmen Sie aus diesen Angaben das Massenträgheitsmoment JP
der Scheibe.
Experiment (B)
Anschließend wird die Feder entfernt und die Scheibe mit horizontaler Drehachse
durch P im Schwerefeld der Erde zu Pendelbewegungen angeregt.
(c) Für wiederum Z = 10 Schwingungen in dieser Anordnung misst man eine Zeit
von t 2 = 11,0 s . Bestimmen Sie den Abstand d = PS zwischen
Massenmittelpunkt S und Aufhängepunkt P.
(d) Welche Pendellänge L hat ein mathematisches Pendel, das die gleiche
Schwingungsdauer hat wie das Pendel in Experiment (B)?
Schwingungslehre
-1-
Prüfungsaufgabe 16
Schwingungslehre – Prüfungsaufgabe 16 – Kurzlösungen
(a) Drehfederkonstante c ∗ = 2 N m .
(b) Massenträgheitsmoment JP = 0,304 kg m 2 .
(c) Abstand Drehpunkt-Massenmittelpunkt d = PS = 0,100 m .
(d) Fadenpendel – Fadenlänge L = 0,306 m .
Schwingungslehre
-2-
Prüfungsaufgabe 16
Schwingungslehre – Prüfungsaufgabe 16 – Musterlösung
(a) Für ein lineares Momentengesetz gilt – mit der Drehfederkonstante c ∗ als
Proportionalitätskonstante – für den Zusammenhang zwischen äußerem
Drehmoment M ext und Winkelauslenkung β
M ext = c ∗ β
(analog zum HOOKEschen Gesetz für eine ideale Feder Fext = c y )
daraus wird (der Drehwinkel ist im Bogenmaß einzusetzen)
π
Nm
M
c ∗ = ext = 2
= 2 Nm
π
β
4
(b) Die Schwingungsdauer eines Drehpendels bestimmt sich aus
Massenträgheitsmoment J und Drehfederkonstante c ∗ gemäß
JP
T0Dreh = 2π
c
(analog zum Federpendel T0Federpendel = 2π
∗
m
)
c
daraus erhält man für das Massenträgheitsmoment
JP =
c ∗T0 2
4π 2
=
2 (kg m s −2 ) m ⋅ 2,45 2 s 2
4π 2
= 0,304 kg m 2
(c) Die Schwingungsdauer eines physikalischen Pendels unter der Einschränkung
’kleine Auslenkungen’ (nach Linearisierung der Differentialgleichung) ist gegeben
durch
T0phys = 2π
JP
mgd
mit m Gesamtmasse
g Schwerebeschleunigung
d Abstand zwischen Drehpunkt P und Massenmittelpunkt S
JP Massenträgheitsmoment bezüglich des Drehpunkts P
Quadrieren und Auflösen nach dem Abstand Drehpunkt-Massenmittelpunkt d = PS
liefert
d =
4π 2 J P
m g (T0phys ) 2
=
4π 2 ⋅ 0,304 kg m 2
10 kg ⋅ 10 m s − 2 ⋅ 1,12 s 2
= 0,100 m
Schwingungslehre
-3-
Prüfungsaufgabe 16
(d) Ein Fadenpendel hat, wieder unter der Einschränkung ’kleine Auslenkungen’ aus
der Ruhelage (nach Linearisierung der Differentialgleichung) eine Schwingungsdauer
von
T0math = 2π
L
g
mit L Länge des Pendels
g Schwerebeschleunigung
mit der Forderung
T0phys = T0math
wird nach Quadrieren und Umstellung die Fadenlänge
L=
(T0phys ) 2 g
4π 2
=
1,12 s 2 ⋅10 m s − 2
4π 2
= 0,306 m
Schwingungslehre
-4-
Prüfungsaufgabe 16
Schwingungslehre – Prüfungsaufgabe 17
An einer langen Schraubenfeder ist ein hantelförmiger Körper angeschweißt (vgl. Skizze). Dieses
Feder-Masse-System kann vertikale Längsschwingungen und gleichzeitig Drehschwingungen
um die Federachse ausführen. Die beiden
Schwingungszustände sind über die gemeinsame
Feder miteinander gekoppelt. Nach WILBERFORCE
kann man die besonderen Phänomene der Kopplungsschwingungen dann deutlich demonstrieren,
wenn die Eigenfrequenzen der Längs- und der
Drehschwingung gleich sind. In diesem Fall treten
(bei geeigneten Anfangsbedingungen) Schwebungen auf und die Energie oszilliert von einem
Schwingungszustand in den anderen und wieder
zurück.
m = 0,032 kg
L = 0,04 m
r = 0,01 m
c; c ∗
r
g
r
m
L
L
m
(a) Belastet man die Feder mit der Gewichtskraft der Hantel (vgl. Skizze), dann verlängert sich die Feder um s1 = 0,37 m . Die Hantel besteht aus einem – idealisierend masselosen – Stab und den beiden Kugeln. Berechnen Sie die Eigenkreisfrequenz ω0,L für die vertikalen ungedämpften Längsschwingungen des Federpendels.
(b) Dreht man in der Ruhelage die Hantel fünf Mal vollständig um die vertikale
Schraubenachse, dann ist dazu ein äußeres Drehmoment von
M ext = 5,6 ⋅ 10 −2 N m aufzuwenden, um die Hantel statisch ruhig zu halten. Welche Eigenkreisfrequenz ω0,Dr haben reine Drehschwingungen der Hantel?
(c) Mit den angegebenen Maßen ist die Bedingung für ausgeprägte Kopplungsschwingungen (Schwebungen) nicht erfüllt. Welcher Abstand Lres der Kugeln von
der Drehachse muss eingestellt werden, damit ω0,Dr = ω0,L gilt?
Schwingungslehre
-1-
Prüfungsaufgabe 17
Schwingungslehre – Prüfungsaufgabe 17 – Kurzlösungen
(a) Federkonstante c = 1,70 Nm .
Längsschwingungen – Eigenkreisfrequenz ω0,L = 5,15 s -1 .
(b) Drehfederkonstante (oder Winkelrichtgröße) c * = 1,79 ⋅ 10 −3 N m (rad-1 ) ;
Massenträgheitsmoment (STEINER) J = 1,05 ⋅ 10 −4 kg m 2 ;
Drehschwingungen – Eigenkreisfrequenz ω0,Dr = 4,13 s −1 .
(c) Resonanzbedingung ω0,Dr = ω0,L .
2
Massenträgheitsmoment J res = 2mLres 2 + 2 mr 2 ;
5
Resonanz – Länge Lres = 3,31 cm .
Schwingungslehre
-2-
Prüfungsaufgabe 17
Schwingungslehre – Prüfungsaufgabe 17 – Musterlösung
(a) Die Federkonstante c für die Längsschwingungen ergibt sich für eine ideale Feder nach HOOKE aus der äußeren Kraft Fext , hier der Gewichtskraft der beiden Ku-
geln, und der sich einstellenden Auslenkung s1
Fext = c s1
mit
Fext = Fgrav = 2 m g
wird
c=
Fgrav
s1
=
2mg 2 ⋅ 0,032 kg ⋅ 9,81ms -2
=
0,37 m
s1
= 1,697 Nm
Die Eigenkreisfrequenz ω0L für Längsschwingungen des Feder-Masse-Systems ergibt sich aus Federkonstante c und der Masse (2m ) der angehängten Hantel zu
ω0,L =
c
=
2m
g
2m g 1
9,81 ms − 2
⋅
=
=
s1 2 m
s1
0,37 m
= 5,149 s -1
(b) Die Drehfederkonstante (oder Winkelrichtgröße) c * ergibt sich für eine ideale
Drehfeder aus dem äußeren Drehmoment M ext und dem sich dadurch einstellenden
Auslenkwinkel ϕ1
M ext = c * ϕ1
also für ϕ1 = 5 ⋅ 2π (rad)
c* =
(Drehwinkelangabe im Bogenmaß)
M ext 5,6 ⋅ 10 −2 Nm
=
ϕ1
5 ⋅ 2π
= 1,789 ⋅ 10 − 3 N m (rad -1 )
Die Eigenkreisfrequenz ω0,Dr für Drehschwingungen des Drehpendel-Systems ergibt
sich aus Drehfederkonstante c * und dem Massenträgheitsmoment J der angehängten Hantel zu
ω0,Dr =
Schwingungslehre
c*
J
-3-
Prüfungsaufgabe 17
Das Massenträgheitsmoment der Hantel mit zwei Kugeln ist mit STEINER-Anteil (die
Kugeln sind um die Strecke L aus der Drehachse verschoben)
2
2
2
J = 2 [ mr 2 + mL2 ] = 2 m [ r 2 + L2 ] = 2 ⋅ 0,032 kg ⋅ [ ⋅ (1,0 ⋅ 10 − 2 m) 2 + ( 4,0 ⋅ 10 − 2 m) 2 ]
5
5
5
= 0,064 kg ⋅ [0,4 + 16] ⋅ 10 − 4 m 2
= 1,050 ⋅ 10 − 4 kg m 2
damit wird die Eigenkreisfrequenz ω0,Dr der Drehschwingungen
c*
1,789 ⋅ 10 − 3 (kg m s - 2 ) m
=
= 17,04 s − 2
−
4
2
J
1,050 ⋅ 10 kg m
ω0,Dr =
= 4,128 s −1
(c) Die Resonanzbedingung ω0,Dr = ω0,L ist erfüllt für
c
c*
=
2 m J res
oder umgeformt
c*
2m
= J res
c
Das Massenträgheitsmoment J res erhält man analog zu Teilaufgabe (b) für eine Verschiebung der Kugeln um Lres aus der Drehachse
2
J res = 2mLres 2 + 2 mr 2
5
Eingesetzt ergibt sich
2
c*
= 2mLres 2 + 2 mr 2
5
c
2
c*
= Lres 2 + r 2
5
c
damit wird die erforderliche Länge für die Resonanzbedingung
2m
Lres 2 =
c * 2 2 1,789 ⋅ 10 −3 N m
2
− r =
−
⋅ (1,0 ⋅ 10 −2 m)2 = (10,54 + 0,40 ) ⋅ 10 − 4 m2
1
c 5
5
1,697 Nm
= 10,94 ⋅ 10 − 4 m2
und schließlich
Lres = 3,307 cm
Schwingungslehre
-4-
Prüfungsaufgabe 17
Schwingungslehre – Prüfungsaufgabe 18
β
Das skizzierte schwingungsfähige
System besteht aus einer dünnen
Stange, die im Punkt D reibungsfrei
gelagert ist. Die – idealisierend als
masselos zu betrachtende – Stange trägt
oberhalb des Drehpunktes D im Abstand
L = 0,30 m eine Kugel (Masse
m = 3,50 kg ; Radius r = 0,050 m ).
D
An der Stange ist in D eine Spiralfeder
angebracht, die in der senkrechten Lage
β 0 = 0 kein Drehmoment ausübt.
r
L
m
Die Drehfederkonstante ist c 0 ∗ = 45 Nm .
Das System schwingt im Schwerefeld
der Erde.
(a) Berechnen Sie die Eigenfrequenz f01 für freie ungedämpfte Schwingungen um
die stabile Lage β 0 = 0 für kleine Winkelamplituden.
(b) Wenn die Drehfederkonstante c ∗ klein wird, kann das System bei β 0 = 0 labil
werden. Das System schwingt dann nicht mehr um diese senkrechte Lage.
∗
Berechnen Sie die Federkonstante c1 , bei der die Stabilität gerade
verschwindet.
Für c 0 ∗ < c1∗ besitzt das System bei den Winkelpositionen β1 = βrechts und
β 2 = − βlinks auf der rechten und der linken Seite zwei stabile Gleichgewichtslagen.
∗
(c) Welchen Wert muss die Drehfederkonstante c 2 haben, damit die Stange in
diesen beiden Gleichgewichtslagen gerade waagrecht liegt?
(d) Berechnen Sie die Eigenfrequenz f02 für freie ungedämpfte Schwingungen um
π
die rechte Gleichgewichtslage β1 = (in der Näherung für kleine Amplituden).
2
π
Hinweis und Lösungshilfe: Setzen Sie β = ( + γ ) und geben Sie die Gleichungen
2
für einen kleinen Auslenkwinkel γ an.
Schwingungslehre
-1-
Prüfungsaufgabe 18
Schwingungslehre – Prüfungsaufgabe 18 – Kurzlösungen
(a) Drehmoment (linearisiert) M res = M rück + M ausl = − c 0 ∗ β + (m g ) ⋅ (Lβ) .
&& .
Differentialgleichung (linearisiert): − c 0 ∗ β + mgLβ = J D β
Massenträgheitsmoment (STEINER) J D = 3,19 ⋅ 10 −1 kg m 2 .
Eigenkreisfrequenz ω01 = 10,4 s −1 ; Eigenfrequenz f01 =
2
(b) Grenzbedingung für Stabilität nach (a) ω01 =
ω01
= 1,66 s −1 .
2π
c 0 ∗ − mgL
= 0.
JD
∗
Drehfederkonstante c1 = m g L = 0,30 N m .
r
r
(c) Gleichgewichtsbedingung M rück = M ausl .
∗
Drehfederkonstante c 2 = 6,56 Nm .
(d) Gleichgewichtsbedingung (vgl. Teilaufgabe (c)): (c 2 ∗
Schwingungsdifferentialgleichung &γ& +
π
− m g L) = 0 .
2
c 2∗
γ =0.
JD
Eigenkreisfrequenz ω02 = 4,54 s −1 ; Kreisfrequenz f02 = 0,722 s −1 .
Schwingungslehre
-2-
Prüfungsaufgabe 18
Schwingungslehre – Prüfungsaufgabe 18 – Musterlösung
(a) Bei Auslenkung des schwingungsfähigen Systems aus der vertikalen Ruhelage
wirken folgende Drehmomente (Vorzeichen und Beträge) auf die Anordnung
•
ein rückstellendes Drehmoment (negatives Vorzeichen) der Drehfeder
(analog dem HOOKEschen Gesetz für eine ideale Feder),
M rück = − c 0 ∗ β
•
ein auslenkendes Drehmoment (positives Vorzeichen) durch die
Massenverteilung des Systems
M ausl = (m g ) (L sin β)
Für kleine Auslenkwinkel aus der Ruhelage, also für β << 1 , gilt näherungsweise
sin β ≈ β (Reihenentwicklung der Sinus-Funktion)
Damit wird näherungsweise
M ausl = (m g ) ⋅ (Lβ)
Das resultierende gesamte Drehmoment wird
M ges = M rück + M ausl = − c 0 ∗ β + ( m g ) ⋅ (Lβ)
Drehmomente bewirken nach NEWTON eine Winkelbeschleunigung gemäß
&&
M
=J α=J β
ges
D
D
Zusammengenommen ergibt sich also (beschränkt auf die Näherung für kleine
Auslenkungen aus der Ruhelage zur Linearisierung der Differentialgleichung)
&&
− c0∗ β + m g L β = JD β
oder
∗
&& + (c 0 − mgL) β = 0
β
JD
Diese lineare Differentialgleichung ist vom Typ der StandardSchwingungsdifferentialgleichung
y&& + ω0 2 y = 0
Koeffizientenvergleich liefert für die Eigenkreisfrequenz die Beziehung
ω012 =
c 0 ∗ − mgL
JD
Das Massenträgheitsmoment J D des Systems wird unter Anwendung des
STEINERschen Satzes
JD =
2
m r 2 + m L2 = 0,4 ⋅ 3,50 kg ⋅ 25,0 ⋅ 10 − 4 m 2 + 3,50 kg ⋅ 9,0 ⋅ 10 − 2 m 2
5
= 35,0 ⋅ 10 − 4 kg m 2 + 31,5 ⋅ 10 − 2 kg m 2
= 3,19 ⋅ 10 −1 kg m 2
Schwingungslehre
-3-
Prüfungsaufgabe 18
Damit erhält man
ω012 =
c 0 ∗ − mgL 45,0 N m − 3,50 kg ⋅ 9,81 m s −2 ⋅ 0,30 m (45,0 − 10,3 ) kg m 2 s −2
=
=
JD
0,319 kg m 2
0,319 kg m 2
= 108,8 s − 2
und die Eigenkreisfrequenz
ω01 = 10,4 s −1
daraus ergibt sich die Eigenfrequenz
f01 =
ω01
= 1,66 s −1
2π
Mit kleiner werdender Drehfederkonstante c 0 ∗ kann das System 'kippen'. Die
Grenzbedingung für Stabilität ist erreicht, wenn in der Beziehung für die
Eigenkreisfrequenz nach Teilaufgabe (a)
ω012
c 0 ∗ − mgL
=
JD
der Zähler verschwindet, also null wird.
∗
Diese Bedingung für Kippen liefert für die zugehörige Drehfederkonstante c1
c0∗ − m g L = 0
Die Drehfederkonstante c1 * bestimmt sich zu
c1∗ = m g L = 3,50 kg ⋅ 9,81 m s −2 ⋅ 0,30 m
= 0,30 N m
(c) Die Gleichgewichtsbedingung fordert, dass das resultierende GesamtDrehmoment verschwindet, also gilt
r
M
∑ =0
Damit gilt für die Beträge des rücktreibenden und des auslenkenden Drehmoments
die Forderung
r
r
M rück = M ausl
Für die waagrechte Lage, also für β rechts =
r
M ausl = L (m g )
und
π
ist
2
r
π
M rück = c 2 ∗
2
damit wird
L (m g ) = c 2 ∗
Schwingungslehre
π
2
-4-
Prüfungsaufgabe 18
und
2
2
⋅ m g L = ⋅ 3,50 kg ⋅ 9,81 ms − 2 ⋅ 0,30 m
π
π
= 6,56 Nm
c 2∗ =
(d) In Analogie zu Teilaufgabe (a) gilt
&& = − c ∗ β + m g L sin β
JD β
2
π
Mit der Setzung β = ( + γ ) wird daraus
2
d2 π
π
π
( + γ ) = − c 2 ∗ ( + γ ) + m g L sin( + γ )
2 2
2
2
dt
π
oder mit der trigonometrischen Identität sin( + γ ) = cos γ umgeschrieben
2
π
J D &γ& = − c 2 ∗
− c 2 ∗ γ + m g L cos γ
2
Für kleine Auslenkwinkel aus der neuen Ruhelage, also für γ << 1 , gilt die Näherung
JD
cos γ ≈ 1
(Reihenentwicklung der Kosinus-Funktion)
wird
π
− m g L)
2
Der Klammerausdruck auf der rechten Seite verschwindet, denn nach der
Gleichgewichtsbedingung von Teilaufgabe (c) gilt
J D &γ& = − c 2 ∗ γ − (c 2 ∗
π
− m g L) = 0
2
Es bleibt damit die Schwingungsdifferentialgleichung
(c 2 ∗
&γ& +
c 2∗
γ=0
JD
Für das Quadrat der Eigenkreisfrequenz erhält man durch Koeffizientenvergleich mit
der Standard-Differentialgleichung für ungedämpfte Schwingungen
ω02
2
c 2 ∗ 6,56 (kg m s −2 ) m
=
=
JD
0,319 kg m 2
= 20,56 s − 2
Daraus erhält man die Eigenkreisfrequenz
ω02 = 4,54 s −1
und die Kreisfrequenz
f02 =
ω02 4,54 s −1
=
= 0,722 s −1
2π
2π
Schwingungslehre
-5-
Prüfungsaufgabe 18
Schwingungslehre – Prüfungsaufgabe 19
Eine Analysenwaage aus dem physikalischen Praktikum (vgl. Abb. 1) soll durch ein
leichter zu berechnendes Modell (vgl. Abb. 2) simuliert werden. Der Waagebalken
mit Schalen und Gewichten wird ersetzt durch eine lange dünne Stange der Länge
LSt und Masse mSt (der Radius der Stange ist wesentlich kleiner als die Länge). Der
Zeiger wird ebenfalls simuliert durch eine sehr dünne Stange der Länge LZ und der
Masse m Z .
Abb. 1
Abb. 2
LSt
D
LZ
β
r
g
Daten zur Geometrie und den Massen der Körper:
Waagebalken: Masse mSt = 120 g , Länge LSt = 30 cm .
Zeiger:
Masse mZ = 25 g ,
Länge LZ = 20 cm .
(a) Berechnen Sie das Massenträgheitsmoment J D des starren Systems
Waagebalken mit Zeiger bezüglich der Drehachse durch D senkrecht zur
Zeichenebene. Das Massenträgheitsmoment einer langen dünnen Stange für
eine Achse durch den Schwerpunkt (senkrecht zur Zeichenebene) ist
1
JS =
m L2 .
12
(b) Stellen Sie die Differentialgleichung für ungedämpfte Drehschwingungen (sehr)
kleiner Amplitude auf.
(c) Berechnen Sie die Eigenkreisfrequenz ω0 und die Schwingungsdauer T0 des
Modell-Systems.
Durch Reibungsverluste sind die Schwingungen der Waage schwach gedämpft. Man
beobachtet, dass die Ausschläge nach jeweils sieben Schwingungen auf ein Fünftel
des Anfangswertes abnehmen.
(d) Bestimmen Sie den Dämpfungsgrad D und den Abklingkoeffizienten δ .
(e) Um welchen Anteil (Prozentangabe) ist die Schwingungsdauer Td der
gedämpften Schwingung größer als die der ungedämpften Schwingung T0 ?
Schwingungslehre
-1-
Prüfungsaufgabe 19
Schwingungslehre – Prüfungsaufgabe 19 – Kurzlösungen
(a) Massenträgheitsmoment Stange J St,D = 9,0 ⋅ 10 −4 kg m 2 .
Massenträgheitsmoment Zeiger J Z,D = 3,33 ⋅ 10 −4 kg m 2 .
Gesamtes Massenträgheitsmoment J D = 1,23 ⋅ 10 −3 kg m 2 .
(b) Rücktreibendes Drehmoment Zeiger
(linearisiert) Mrück = − (mz g ) ⋅ (
Lz
L
sin β) ≈ − mz g z β .
2
2
&& + mz g Lz β = 0 .
Differentialgleichung (linearisiert) β
2J D
(c) Eigenkreisfrequenz ω0 = 4,47 s −1; Schwingungsdauer T0 =
2π
= 1,41 s .
ω0
(d) Abklingkoeffizient δ = 0,164 s −1 ; Dämpfungsgrad D = 3,67 ⋅ 10 −2 < 0,1 .
(e) Schwingungsdauern (Reihenentwicklung)
Td =
T0
1− D 2
Schwingungslehre
≈ (1 +
1 2
D )T0 ≈ 1,001⋅ T0 . Abweichung weniger als 0,1 %.
2
-2-
Prüfungsaufgabe 19
Schwingungslehre – Prüfungsaufgabe 19 – Musterlösung
Vorbemerkung zum angegebenen Modell: Der Begriff ’Stange’ beinhaltet, dass die
Querabmessungen sehr klein sind gegen die Länge der Stange; dabei ist die
geometrische Form des Querschnitts (rechteckig, rund oder x-Profil) unerheblich. Bei
der Berechnung des Massenträgheitsmoments geht die Querschnittsfläche in das
Volumen und damit in die Gesamtmasse ein.
Sind die Querabmessungen nicht mehr vernachlässigbar, z. B. für einen Backstein,
dann gehen in die Massenträgheitsmomente zwei Abmessungen ein.
(a) Der Waagebalken dreht sich – aus Symmetriegründen – um eine Achse durch
den eigenen Schwerpunkt. Für das Massenträgheitsmoment gilt mit r << L , also für
eine Stange
J St,D =
1
1
mSt LSt 2 =
⋅ 0,120 kg ⋅ (0,30 m) 2
12
12
= 9,0 ⋅ 10 − 4 kg m 2
Der Zeiger dreht sich um eine Achse durch seinen Endpunkt repräsentiert durch eine
ebenfalls dünne Stange. Nach STEINER ist das Massenträgheitsmoment des Zeigers
bezüglich des Drehpunkts D
J Z,D =
L
1
1
1
m z ⋅ Lz 2 + m z ⋅ ( z ) 2 = m z ⋅ Lz 2 = ⋅ 25 ⋅ 10 − 3 kg ⋅ (0,20 m) 2
3
3
12
2
= 3,33 ⋅ 10 − 4 kg m 2
Das gesamte Massenträgheitsmoment des Modells bezüglich einer Drehachse durch
D wird damit
J D = J St,D + J Z,D = (9,0 + 3,33) ⋅ 10 −4 kg m 2
= 1,23 ⋅ 10 − 3 kg m 2
(b) Der Waagebalken ist in seinem Massenmittelpunkt gelagert; es wird aus
Symmetriegründen von ihm kein resultierendes Moment ausgeübt. Für jedes
Masseteilchen, das ein rechtsdrehendes Drehmoment ausübt, gibt es aus
Symmetriegründen ein Masseteilchen, das ein betragsmäßig gleiches
linksdrehendes Drehmoment ausübt.
Ein rücktreibendes Drehmoment kommt allein durch die Auslenkung des
Massenmittelpunkts des Zeigers aus der Ruhelage zustande. Dieses Drehmoment
ist
Lz
L
sin β) ≈ − mz g z β
2
2
mit der Linearisierung für kleine Auslenkwinkel aus der Ruhelage also für β << 1 wird
M rück = − (mz g ) ⋅ (
sin β ≈ β
(Reihenentwicklung der Sinus-Funktion)
Das NEWTONsche Grundgesetz für Drehbewegungen lautet
&&
M
=J β
res
Schwingungslehre
D
-3-
Prüfungsaufgabe 19
Mit den obigen Beziehungen für M res = M rück und J D folgt daraus
− mz g
Lz
&&
β = JD β
2
oder
&& + mz g Lz β = 0
β
2JD
(c) Durch Koeffizientenvergleich mit der Standard-Differentialgleichung
&& + ω 2β = 0
β
0
erhält man für das Quadrat der Eigenkreisfrequenz
ω0 2 =
m z g Lz 25 ⋅ 10 −3 kg ⋅ 9,81 m s −2 ⋅ 0,20 m
=
2 JD
2 ⋅ 1,23 ⋅ 10 − 3 kg m 2
= 20,0 s − 2
und die Eigenkreisfrequenz
ω0 = 4,47 s −1
und die Schwingungsdauer für die ungedämpfte Schwingung des Modellsystems
2π
= 1,41 s .
T0 =
ω0
(d) Die Schwingungen eines viskos gedämpften Systems lassen sich darstellen als
ϕ = ϕmax ⋅ e −δ t cos( ωdt + ϕ 0 )
oder
ϕ = ϕmax ⋅ e −δ t sin( ωdt + ϕ 0 )
Für das Abklingen der Auslenkungen braucht man jeweils nur die einhüllende
Exponentialfunktion zu untersuchen; also den Zeitverlauf von
ϕ einh = ϕmax e −δt
oder
ϕ einh
= e − δt
ϕmax
Logarithmieren liefert
⎛ϕ
⎞
ln ⎜⎜ einh ⎟⎟ = − δ t
⎝ ϕmax ⎠
bei schwacher Dämpfung ist Td ≅ T0 (diese Annahme muss am Ende überprüft
werden).
Schwingungslehre
-4-
Prüfungsaufgabe 19
ϕ einh 1
=
für jeweils sieben Schwingungsperioden, also für ein
ϕmax 5
Zeitintervall t = 7 ⋅ T0 wird der Abklingkoeffizient
Mit den Vorgaben
⎛ 1⎞
ln⎜ ⎟
ln1 − ln 5
ln 5
5
δ=− ⎝ ⎠ =−
=
7 ⋅ 1,41 s
7 ⋅ 1,41 s 7 ⋅ 1,41 s
= 0,164 s −1
Der Dämpfungsgrad ergibt sich aus Abklingkoeffizient δ und Eigenkreisfrequenz ω0
zu
D=
δ
0,164 s −1
=
ω0
4,47 s −1
= 3,67 ⋅ 10 − 2
Damit liegt mit einem Dämpfungsgrad 0 < D ≤ 0,10 für das System ’schwache
Dämpfung’ vor und die benutzte Näherung Td = T0 war gerechtfertigt.
(e) Die Eigenkreisfrequenzen und die Schwingungsdauern für die Bedingungen mit
und ohne Dämpfung sind über den Dämpfungsgrad miteinander verknüpft
ωd
T
= 1− D 2 = 0 ,
ω0
Td
wegen T =
2π
ω
damit wird schließlich
Td =
T0
1− D 2
= 1,001 ⋅ T0
Da die Berechnung – wegen D << 1 – an die Grenzen Ihres Taschenrechners stößt,
benutzt man zweckmäßigerweise und vorteilhaft die Reihenentwicklung für
1
1− x
= 1+
1
1⋅ 3 2 1⋅ 3 ⋅ 5 3
x+
x +
x + ... ( x entspricht D 2 )
2
2⋅4
2⋅4⋅6
bricht die Reihenentwicklung nach dem linearen Glied ab, dann erhält man – und
dies fast ganz ohne Taschenrechner! –
Td =
T0
1− D2
≈ 1,001 ⋅ T0
≈ (1 +
1 2
1
D )T0 = [1 + (3,67 ⋅ 10 −2 ) 2 ] T0 = (1 + 6,7 ⋅ 10 − 4 )T0
2
2
Die beiden Schwingungsdauern Td und T0 für den gedämpften und den
ungedämpften Schwingfall weichen um weniger als 0,1 % voneinander ab.
Schwingungslehre
-5-
Prüfungsaufgabe 19
Schwingungslehre – Prüfungsaufgabe 20
Ein Rad hat die Masse m = 1,5 kg , den Innendurchmesser d i = 180 mm und den
Außendurchmesser d a = 220 mm .
In einem ersten Versuch (vgl. Skizze 1) wird das Rad an einem Nagel im Punkt A
aufgehängt. Man lässt es (bei kleinen Auslenkwinkeln aus der Ruhelage) im Schwerefeld der Erde pendeln. Die gemessene Periodendauer aus mehreren Messungen
ist T0a = 1,20 s .
(a) Bestimmen Sie das Massenträgheitsmoment J S bezüglich der Radachse durch
den Massenmittelpunkt.
P1
A
a1
c1
S
di
S
S
da
c2
P2
a2
Skizze 2
Skizze 1
In einem zweiten Versuch (vgl. Skizze 2) wird das Rad im Schwerpunkt S reibungsfrei gelagert. In den Punkten P1 und P2 sind Federn mit den Federkonstanten
c1 = c 2 = c = 1,20 N cm −1 befestigt. Im Ruhezustand bilden die starren Verbindungen
a1 und a2 Tangenten an den äußeren Radumfang.
(b) Stellen Sie die Differentialgleichung für die Drehschwingungen des Rades auf.
Dies soll wieder unter der Voraussetzung kleiner Winkelausschläge erfolgen.
(c) Berechnen Sie die Eigenkreisfrequenz ω0c und die Periodendauer T0c der Drehschwingungen um S.
Aufstecken von zwei Flügeln (Masse vernachlässigbar) auf die Felge führt zu einer
Dämpfung des schwingungsfähigen Systems. Man beobachtet anschließend, dass
die Winkelausschläge in jeweils fünf Schwingungsperioden auf die Hälfte des Anfangswerts abnehmen.
(d) Bestimmen Sie den Dämpfungsgrad D des Systems.
Schwingungslehre
-1-
Prüfungsaufgabe 20
Schwingungslehre – Prüfungsaufgabe 20 – Kurzlösungen
(a) Massenträgheitsmoment (STEINER) J A =
mdg
ω0a
2
=
m Ri g T0a
4 π2
.
Massenträgheitsmoment J S = 3,62 ⋅ 10 −2 kg m 2 .
(b) Kleiner Auslenkwinkel β ; Bogenlänge Ra = Federdehnung y ; β =
y
.
Ra
Federn in Parallelanordnung c res = 2 c .
Rücktreibendes Drehmoment M rück = − 2 [c y ] Ra = − (2 c Ra 2 ) β .
2
&& + 2 c Ra β = 0 .
Differentialgleichung β
JS
(c) Eigenkreisfrequenz ω0c = 8,96 s −1 ; Schwingungsdauer T0c = 0,70 s .
(d) Abklingkoeffizient δ = 0,198 s −1 .
Dämpfungsgrad D = 0,022 < 0,1 (schwache Dämpfung).
Schwingungslehre
-2-
Prüfungsaufgabe 20
Schwingungslehre – Prüfungsaufgabe 20 – Musterlösung
(a) Für ein physikalisches Pendel gilt bei kleinen Auslenkwinkeln aus der Ruhelage
für das Quadrat der Eigenkreisfrequenz ω0a
ω0a 2 =
md g
JA
mit
m Gesamtmasse des Pendels
d Abstand zwischen Aufhängepunkt A und Massenmittelpunkt S
D
d = AS = Ri = i halber Innendurchmesser
2
g Fallbeschleunigung
J A Massenträgheitsmoment der Anordnung bezüglich einer Achse durch
den Aufhängepunkt A
Der Zusammenhang zwischen Eigenkreisfrequenz ω0a und Schwingungsdauer T0a
ist
1
ω0a = 2π ⋅
T0a
Daraus erhält man das Massenträgheitsmoment J A bezüglich des
Aufhängepunkts A
JA =
mdg
ω0a
2
=
m Ri g T0a
4 π2
Das Massenträgheitsmoment J A bezüglich des Aufhängepunkts und das Massenträgheitsmoment J S bezüglich des Massenmittelpunkts S sind über den STEINERschen Satz verknüpft
J A = J S + ma 2
dabei ist
a = Ri der Abstand AS
Daraus wird
JS = (
T0a 2
4π 2
2
m Ri g ) − ( m Ri ) = m Ri (
= 1,50 kg ⋅ 9,0 ⋅ 10 − 2 m ⋅ (
= 1,35 ⋅ 10
−1
1,20 2 s 2
4π
2
T0a 2
4π 2
g − Ri )
⋅ 9,81 m s − 2 − 9,0 ⋅ 10 − 2 m)
kg m ⋅ (0,365 − 0,09) m
= 3,62 ⋅ 10 − 2 kg m 2
(b) Die tangential am Außendurchmesser angreifenden Federkräfte üben ein Drehmoment auf das Rad aus und bewirken Drehschwingungen. Da für eine ideale Feder
Stauchung und Dehnung äquivalent sind, addieren sich die von den beiden Federn
ausgeübten Drehmomente in Parallelschaltung.
Schwingungslehre
-3-
Prüfungsaufgabe 20
Bei Linksdrehung des Rades wird die obere Feder gedehnt und die untere um den
gleichen Betrag gestaucht; beide Auslenkungen bewirken ein rücktreibendes Drehmoment.
Den Zusammenhang zwischen der linearen Auslenkung y einer der beiden Federn
und dem Drehwinkel β liefert die Definition des Winkels im Bogenmaß, also
Winkel ϕ =
Bogenlänge s Federdehnu ng y
=
Radius R
Außenradiu s R a
denn für kleine Auslenkwinkel β ist die Bogenlänge gleich der Federdehnung y . Also gilt
β=
y
Ra
oder
y = Ra ⋅ β
Die von einer Feder ausgeübte rücktreibende Kraft ist mit c1 = c 2 = c
Frück = − c y
Das von beiden Federn ausgeübte rücktreibende Drehmoment wird damit
M rück = −2 [c y ] Ra = −(2 c Ra 2 )β
(eine Feder wird gedehnt, eine gestaucht, d. h. die Federn sind in Parallelanordnung).
Nach dem NEWTONschen Grundgesetz für Drehbewegungen bewirken Drehmomente
Winkelbeschleunigungen gemäß
&&
M
=J α=J β
res
S
S
dabei ist
M rück = M res
Das ergibt (unter der Einschränkung kleiner Auslenkwinkel β und angenommener
Reibungsfreiheit) die Differentialgleichung einer harmonischen, ungedämpften Drehschwingung
&& + 2 c R 2β = 0
JS β
a
2
&& + 2 c Ra β = 0
β
JS
(c) Für die Eigenkreisfrequenz des Systems erhält man durch Koeffizientenvergleich
mit der Standard-Gleichung für ungedämpfte Schwingungen
y&& + ω0 2 y = 0
für das Quadrat der Eigenkreisfrequenz
ω0c
2
2 c Ra 2 2 ⋅ 1,2 kg m s −2 (10 −2 m) −1 ⋅ 0,112 m 2
=
=
JS
3,62 ⋅ 10 − 2 kg m 2
= 80,22 s − 2
Schwingungslehre
-4-
Prüfungsaufgabe 20
und für die Eigenkreisfrequenz
ω0c = 8,96 s −1
Damit wird die Schwingungsdauer
T0c =
2π
2π
=
ω0c 8,96 s −1
= 0,70 s
(d) Die Abnahme der Winkelausschläge in gleichen Zeitintervallen um jeweils den
gleichen Faktor ist Kennzeichen eines Reibungsmoments, das proportional zur Winkelgeschwindigkeit ist; dies führt zu einer exponentiellen Abnahme der Winkelausschläge
β(t ) = βˆ 0 ⋅ e −δt ⋅ cos(ωdt + ϕ 0 )
Es gilt allgemein für die Hüllfunktion
βHüll (t ) = βˆ 0 ⋅ e −δ t
umgeformt und logarithmiert erhält man
⎛ β (t ) ⎞
ln⎜⎜ Hüll ⎟⎟ = −δ t
⎝ βˆ 0 ⎠
Für den vorliegenden Fall wird, zunächst unter der später nachzuprüfenden Annahme schwacher Dämpfung ( 0 < D ≤ 0,1), also für Td ≅ T0c .
⎛ 1⎞
ln⎜ ⎟ = −δ (5Td ) ≅ −δ (5T0c )
⎝2⎠
ln 2
0,693 −1
s
δ=
=
5T0 5 ⋅ 0,70
= 0,198 s −1
Damit wird schließlich der Dämpfungsgrad D
0,198 s −1
δ
=
ω0c
8,96 s −1
= 0,022
D=
Damit wird die oben gemachte Annahme schwacher Dämpfung ( 0 < D ≤ 0,1) bestätigt
und die Näherung Td ≅ T0c gerechtfertigt.
Schwingungslehre
-5-
Prüfungsaufgabe 20
Schwingungslehre – Prüfungsaufgabe 21
Eine Schwingtür ( H = 2,00 m , B = 0,80 m , D = 0,03 m , Dichte ρ = 0,9 g cm −3 ) wird
von einer Torsionsfeder (Winkelrichtgröße c * = 40 N m ) in ihre Ruhelage
zurückgezogen. Die Reibung bei der Rotation um die Achse A sei vernachlässigbar.
A
P
z
L
FR
H
x
B
y
A
D
(a) Bestimmen Sie das Massenträgheitsmoment J A , bezüglich einer Rotation um die
Achse A.
Ein Öldämpfer erzeugt eine geschwindigkeitsproportionale Reibungskraft FR = −b ⋅ v ,
die im Punkt P, mit dem Abstand L = 30 cm von der Achse A tangential angreift.
(b) Wie lautet die Differentialgleichung für gedämpfte harmonische Bewegungen der
Tür.
(c) Welche Schwingungsdauer Td der Tür stellt sich ein, wenn der Betrag des
Reibungskoeffizienten b1 = 110 kg s −1 ist?
Die Schwingtür soll sich von einem vorgegebenen Öffnungswinkel aus ohne
Anfangswinkelgeschwindigkeit schließen.
(d) Wie muss der Reibungskoeffizient b2 gewählt werden, wenn sich die Tür
schnellst möglich schließen soll?
Hinweis: Das Massenträgheitsmoment J z (S) um die z -Achse durch den
m 2
Massenmittelpunkt S ist J z (S) =
(B + D 2 ) .
12
Schwingungslehre
-1-
Prüfungsaufgabe 21
Schwingungslehre – Prüfungsaufgabe 21 – Kurzlösungen
(a) Gesamtmasse m = 43,2 kg .
Massenträgheitsmoment (STEINER) J A = 9,22 kgm 2 .
(b) Rücktreibendes Drehmoment M Rück = − c * β .
Reibungsmoment M Reib = FReib L = − (b1 v ) L = − b1 (ω L ) L = − (b1 L2 ) β& .
2
&& + b1 L β& + c * β = 0 .
Differentialgleichung β
JA
JA
(c) Quadrat der Eigenkreisfrequenz ω0 2 = 4,34 s −2 .
Abklingkoeffizient δ = 0,537 s −1 .
Kreisfrequenz ωd = 2,01 s −1 ; Schwingungsdauer Td = 3,13 s .
(d) Aperiodischer Grenzfall δ = ω0 ;
Reibungskoeffizient bap = b2 = 411 kg s −1 .
Schwingungslehre
-2-
Prüfungsaufgabe 21
Schwingungslehre – Prüfungsaufgabe 21 – Musterlösung
(a) Zur Berechnung des Massenträgheitsmoments braucht man die Gesamtmasse
m der Türe. Diese ergibt sich aus Dichte und Geometrie zu
m = ρ D B H = 900 kg m −3 ⋅ 2,0 m ⋅ 0,8 m ⋅ 3 ⋅ 10 −2 m
= 43,2 kg
Das Massenträgheitsmoment J A für die Bezugsachse A ergibt sich für die
vorgegebene Geometrie aus dem STEINERschen Satz zu
1
1
B
J A = J z (S) + m ( )2 =
m (B 2 + D 2 ) + m B 2
2
12
4
1
1
=
⋅ 43,2 kg ⋅ [(8 ⋅ 10 -1 ) 2 + (3 ⋅ 10 − 2 )2 ] m 2 + 43,2 kg ⋅ (8 ⋅ 10 -1 ) 2 m 2
4
12
= (2,31 + 6,91) kg m 2
= 9,22 kg m 2
(b) Der Betrag des Rückstellmoments M Rück der Torsionsfeder ist proportional zum
Auslenkwinkel β
M Rück = − c * β
Der Betrag des Reibungsmoments M Reib ausgeübt durch den Öldämpfer ist
M Reib = FReib L
Dabei ist die Reibungskraft FReib bei viskoser Reibung proportional zur
Geschwindigkeit und dieser entgegengerichtet
FReib = − b1 v
Der Zusammenhang zwischen Lineargeschwindigkeit v eines Elements der Türe
und der Winkelgeschwindigkeit ω der Türe für einen Abstand L von der Drehachse
ist
v = ωL
Die drei letzten Gleichungen liefern zusammengenommen für den Betrag des
Reibungsmoments
M Reib = FReib L = − (b1 v ) L = − b1 (ω L ) L = − (b1 L2 ) β&
Ein resultierendes Drehmoment aus den Kräften FRück und FReib bewirkt nach
NEWTON eine Winkelbeschleunigung α gemäß
&&
M
=J α=J β
res
A
A
Damit ergibt sich schließlich
M res = M Rück + M Reib
&& = − c * β − b L2 β&
JA β
1
Schwingungslehre
-3-
Prüfungsaufgabe 21
Nach Umstellen erhält man für die Bewegung der Tür die Differentialgleichung einer
viskos gedämpften harmonischen Schwingung
2
&& + b1 L β& + c * β = 0
β
JA
JA
(c) Durch Koeffizientenvergleich mit der allgemeinen Differentialgleichung einer
viskos gedämpften Drehschwingung
&& + 2δ β& + ω 2 β = 0
β
0
erhält man für das Quadrat der Eigenkreisfrequenz ω0
ω0 2 =
c * 40 kg m s −2 m
=
JA
9,21 kg m 2
= 4,34 s − 2
und für den Abklingkoeffizienten δ der gedämpften Schwingung
δ=
b1 L2 110 kg s −1 ⋅ 0,09 m 2
=
2JA
2 ⋅ 9,21 kg m 2
= 0,537 s −1
Für die Kreisfrequenz ω d einer (geschwindigkeitsproportional) gedämpften
Schwingung gilt die Beziehung
ωd 2 = ω0 2 − δ 2 = 4,34 s −2 − 0,29 s −2
= 4,05 s − 2
und
ωd = 2,01 s −1
Damit ergibt sich die Schwingungsdauer der gedämpften Schwingung zu
2π
2π
=
ωd 2,01 s −1
= 3,13 s
Td =
(d) Bei Auslenken und Loslassen ohne eine Anfangswinkelgeschwindigkeit, also mit
ω(t = 0) = β& (t = 0) = 0 ; geht die Tür im aperiodischen Grenzfall am schnellsten unter
einen vorgegebenen Grenzwert zurück (die e-Funktion ist stets ungleich null). Für
den Fall des Loslassens ohne Anfangsgeschwindigkeit geschieht dies ohne
Überschwingen.
Schwingungslehre
-4-
Prüfungsaufgabe 21
Für den aperiodischen Grenzfall ist die Eigenkreisfrequenz ω0 gleich dem
Abklingkoeffizient δ ; also
D=
δ
=1
ω0
oder
δ = ω0
Mit den Werten für den Abklingkoeffizienten δ und der Eigenkreisfrequenz ω0 aus
Teilaufgabe (c) erhält man
b2 L2
ω0 = δ =
2J A
Der Reibungskoeffizient b2 für den aperiodischen Grenzfall wird damit
bap = b2 =
2 J A ω0
L2
=
2 ⋅ 9,21 kg m 2 ⋅ 2,01 s −1
9 ⋅ 10 − 2 m 2
= 411 kg s −1
Schwingungslehre
-5-
Prüfungsaufgabe 21
Schwingungslehre – Prüfungsaufgabe 22
D
d
a
M
A
Eine homogene Kreisscheibe (Masse m = 2 kg , Durchmesser D = 0,5 m ) kann sich
reibungsfrei um ihre horizontale Symmetrieachse drehen. Der Achsenquerschnitt ist
sehr klein und vernachlässigbar.
(a) Welches Massenträgheitsmoment J A, voll hat die Scheibe bezogen auf ihre
Scheibenachse A ?
Aus der Scheibe wird ein kreisrundes Loch geschnitten (Lochdurchmesser
d = 10 cm , die Lochmitte M ist a = 15 cm von der Scheibenachse A entfernt).
(b) Berechnen Sie das neue Massenträgheitsmoment J A,Loch für die gelochte
Scheibe – wieder bezogen auf die Scheibenachse A (vgl. Skizze).
(c) Die fehlende Materie in der Bohrung macht die Scheibe zu einem physikalischen
Pendel. Bestimmen Sie für kleine Auslenkungen aus der Ruhelage die
Winkelrichtgröße c * .
Anleitung: Ein gleich großes zweites, achsensymmetrisch zum ersten in die
Scheibe geschnittenes Loch brächte den Massenmittelpunkt wieder in die
Drehachse A , und damit bliebe die Anordnung frei von Drehmomenten.
(d) Welche Eigenfrequenz f0 hat das ungedämpft schwingende Scheibenpendel mit
Loch?
Schwingungslehre
-1-
Prüfungsaufgabe 22
Schwingungslehre – Prüfungsaufgabe 22 – Kurzlösungen
(a) Massenträgheitsmoment J A, voll = 6,25 ⋅ 10 −2 kg m 2 .
(b) Massenträgheitsmomente J A, voll = J A,Loch + J Loch .
Masse mLoch = 8 ⋅ 10 −2 kg .
Massenträgheitsmoment (Scheibe mit Loch) J A,Loch = 6,06 ⋅ 10 -2 kg m 2 .
(c) Rücktreibendes Drehmoments (linearisiert) M rück = − (mLoch g a β) = − c * β .
Drehfederkonstante c * = mLoch g a = 0,118 N m .
2
(d) Eigenkreisfrequenz ω0 =
c*
J A,Loch
; Eigenfrequenz f0 = 0,222 s −1 .
Schwingungsdauer T0 = 4,50 s .
Schwingungslehre
-2-
Prüfungsaufgabe 22
Schwingungslehre – Prüfungsaufgabe 22 – Musterlösung
(a) Das Massenträgheitsmoment einer homogenen zylindrischen Voll-Scheibe – also
ohne Loch – ist
J A, voll =
1
1
mR 2 = mD 2 = 0,125 ⋅ 2 kg ⋅ (0,5 m) 2
2
8
= 6,25 ⋅ 10 − 2 kg m 2
(b) Massenträgheitsmomente sind additiv. Das Massenträgheitsmoment der VollScheibe J A, voll setzt sich zusammen aus dem Massenträgheitsmoment der Scheibe
mit Loch J A,Loch und dem Massenträgheitsmoment des Lochs J Loch ausgefüllt mit
Materie. Also
J A, voll = J A,Loch + J Loch
Der Anteil des Loches am Massenträgheitsmoment J Loch muss vom
Massenträgheitsmoment J A, voll der Vollscheibe abgezogen werden.
Zur Berechnung von J Loch benötigt man die Masse mLoch des ausgeschnittenen
Lochs. Dazu überlegt man Folgendes: Die Scheibe ist homogen und sie hat überall
die gleiche Dicke; deshalb verhalten sich die Massenanteile wie die zugehörigen
Flächen (Dichte des Materials ρ , Dicke der Scheibe d , Flächenelement ΔA ); also
ΔM = ρV = ρ ΔA d = const. ⋅ ΔA
Damit wird das Verhältnis der Masse des ausgebohrten Lochs mLoch zur Masse der
Scheibe m
mLoch π r 2 d 2
=
=
m
πR 2 D2
Daraus bestimmt sich die Masse mLoch aus der Gesamtmasse m zu
2
2
mLoch
2
⎛ 10 cm ⎞
⎛d ⎞
⎛ 1⎞
⎟⎟ ⋅ 2,0 kg = ⎜ ⎟ ⋅ 2,0 kg
= ⎜ ⎟ m = ⎜⎜
⎝D⎠
⎝5⎠
⎝ 50 cm ⎠
= 8 ⋅ 10 − 2 kg
Das Massenträgheitsmoment für das mit Materie 'gefüllte' Loch ist, einschließlich des
STEINERschen Anteils
1
1
d2
mLoch r 2 + mLoch a 2 = mLoch d 2 + mLoch a 2 = mLoch (
+ a2 )
2
8
8
Das Massenträgheitsmoment für die zylindrische Scheibe mit Loch wird damit
J Loch =
J A.Loch = J A, voll − J Loch
⎛d2
⎞
D2
=m
− mLoch ⎜
+ a2 ⎟
⎜ 8
⎟
8
⎝
⎠
⎛ (10 −1 m) 2
⎞
= 6,25 ⋅ 10 − 2 kg m 2 − 8 ⋅ 10 − 2 kg ⋅ ⎜
+ (1,5 ⋅ 10 −1 m) 2 ⎟
⎜
⎟
8
⎝
⎠
= 6,06 ⋅ 10 - 2 kg m 2
Schwingungslehre
-3-
Prüfungsaufgabe 22
Ein zweites, symmetrisch gebohrtes Loch stellte die Symmetrie wieder her, der
Massenmittelpunkt wäre wieder in der Mitte der Scheibe, also in der Drehachse und
damit ergäbe sich kein resultierendes Drehmoment. Die Scheibe mit Doppelloch
kann frei um die Achse rotieren.
Dieses symmetrisch angeordnete Loch, gefüllt mit Materie, übt nach Auslenken aus
der Ruhelage (der tiefsten Lage unterhalb der Drehachse A gelegen) ein
Drehmoment bezüglich der Drehachse A aus; dieses Drehmoment versucht das
System in die Ruhelage zurück zu treiben.
Der Betrag des Drehmoments ist
M rück = Fgrav a sin β = ( mLoch g ) a sin β
A
A
kein rücktreibendes
Drehmoment
rücktreibendes
Drehmoment
Für kleine Auslenkungswinkel aus der Ruhelage gilt die Näherung
sin β ≈ β
Damit wird der Betrag des rücktreibenden Drehmoments proportional zum
Auslenkwinkel.
M rück = − (mLoch g a β) = − c * β
Dieser lineare Zusammenhang ist Voraussetzung für ungedämpfte harmonische
Schwingungen. Die Proportionalitätskonstante c * entspricht der Drehfederkonstante
für Drehschwingungen; sie ergibt sich zu
c * = mLoch g a = 8 ⋅ 10 −2 kg ⋅ 9,81 m s −2 ⋅ 1,5 ⋅ 10 −1 m
= 0,118 N m
(d) Die Grundgleichung für Drehbewegungen nach NEWTON lautet
M rück = J
d 2β
2
&&
=Jβ
dt
Mit den Teilergebnissen von (b) und (c) folgt
&&
− c *β = J
β
A,Loch
Damit ergibt sich für die Schwingung die Differentialgleichung
&& +
β
c*
J A,Loch
Schwingungslehre
β = 0
-4-
Prüfungsaufgabe 22
Koeffizientenvergleich mit der Standard-Differentialgleichung für harmonische
Drehschwingungen
&& + ω 2β = 0
β
0
liefert als Beziehung für die Eigenkreisfrequenz
ω0 2 =
c*
J A,Loch
Daraus ergibt sich die Eigenfrequenz des physikalischen Pendels – mit der
Einschränkung ’kleine Auslenkungen’ aus der Ruhelage
f0 =
ω0
1
=
2π 2π
c*
J A,Loch
=
1
2π
0,118 kg m s − 2 m
6,06 kg m 2
= 0,222 s −1
oder für die Schwingungsdauer
T0 =
1
1
=
f0 0,222 s
= 4,50 s
Schwingungslehre
-5-
Prüfungsaufgabe 22
Schwingungslehre – Prüfungsaufgabe 23
Auf einer horizontalen geraden Gleitkissenbahn kann sich ein Gleiter ' G 1' (Masse
25
m1 =
kg ) reibungsfrei bewegen. Seine Bewegung wird bestimmt durch eine
9
ideale Feder, die zwischen Gleiter ' G 1' und einer festen Wand angebracht ist (vgl.
Skizze).
G2
C
G1
B
A
Bei entspannter Feder befindet sich der Gleiter ' G 1' am Ort ' B' (sämtliche
Ortskoordinaten werden jeweils von der gleichen Kante des Gleiters aus gemessen).
Eine äußere Kraft ( Fext = 20 N ) drückt die Feder zusammen und verschiebt dabei
den Gleiter ' G 1' um die Strecke BA = y 1 = 20 cm ; der Gleiter ' G 1' befindet sich
danach am Ort ' A ' . Er wird anschließend am Ort ' A ' ohne Anfangsgeschwindigkeit
losgelassen.
(a) Mit welcher Frequenz f01 schwingt der Gleiter ' G 1' nach Loslassen?
(b) Welche Geschwindigkeit v C hat der Gleiter ' G 1' am Ort ' C' ?
1
Der Abstand vom Punkt ' B' ist BC = y 2 =
3 ⋅ y1 .
2
1
Am Ort ' C' steht ein zweiter Gleiter ' G 2' (Masse m2 = m1 ).
4
Bei seiner Schwingungsbewegung stößt Gleiter ' G 1' auf Gleiter ' G 2' . Nach dem
Stoß haften die beiden Gleiter durch einen Klettenverschluss aneinander. Der in der
Zeitspanne des Zusammenstoßes zurückgelegte Weg soll vernachlässigt werden
können.
(c) Welche gemeinsame Geschwindigkeit u gem haben die beiden gekoppelten
Gleiter unmittelbar nach dem Zusammenstoß?
(d) Welche Eigenkreisfrequenz ω02 und welche Schwingungsdauer T02 gehören zu
der Schwingung des gekoppelten Systems nach dem Stoß?
Schwingungslehre
-1-
Prüfungsaufgabe 23
Schwingungslehre – Prüfungsaufgabe 23 – Kurzlösungen
(a) Eigenfrequenz f01 = 0,95 s −1 .
(b) Geschwindigkeit Gleiter Ort – ' C' v C = − 0,60 ms −1 .
(c) Vollständig inelastischer Stoß – gemeinsame Geschwindigkeit
u gem = − 0,48 m s −1 .
(d) Eigenkreisfrequenz ω02 = 5,4 s −1 ; Schwingungsdauer T02 = 1,17 s .
Schwingungslehre
-2-
Prüfungsaufgabe 23
Schwingungslehre – Prüfungsaufgabe 23 – Musterlösung
(a) Für ein lineares Kraftgesetz ist nach HOOKE die Auslenkung proportional zur
angreifenden Kraft
Fext = c y
(die äußere Kraft wirkt in Richtung der Auslenkung);
Eine äußere Kraft Fext = 20 N bewirkt eine Auslenkung aus der Ruhelage der
entspannten Feder um y 1 = 0,20 m . Damit bestimmt sich die Federkonstante einer
idealen Feder zu
c=
Fext
20 N
N
=
= 100
0,2 m
m
y1
Die Eigenkreisfrequenz ω01 bzw. die Schwingungsdauer T01 des Feder-MasseSystems wird eindeutig durch die Kenngrößen des schwingungsfähigen Systems
bestimmt; diese sind
Federkonstante c der Feder und
Masse m1 des Gleiters ' G 1'
Für die Eigenkreisfrequenz ω01 gilt die Beziehung
ω012
c
100 N m −1 900 kg m s −2 m −1
=
=
=
25
m1
25 kg
kg
9
= 36,0 s − 2
und
ω01 = 6,0 s −1
Die Eigenfrequenz wird mit
ω01 = 2π f01
f01 =
ω01 6,0 s −1
=
2π
2π
= 0,95 s −1
(b) Die Schwingungen des Feder-Gleiter-Systems werden durch eine harmonische
Funktion beschrieben. Da die Bewegung aus dem Umkehrpunkt der Schwingung
[ y = yˆ = y 1 ] ohne Anfangsgeschwindigkeit startet, wählt man zweckmäßigerweise zur
allgemeinen Beschreibung eine Kosinus-Funktion
y = yˆ ⋅ cos(ω01t + ϕ0 )
denn dann ist notwendigerweise die Amplitude gleich der Anfangsauslenkung yˆ = y 1
und der Nullphasenwinkel wird vereinfachend ϕ0 = 0 .
Schwingungslehre
-3-
Prüfungsaufgabe 23
Die Zeitabhängigkeit der Geschwindigkeit erhält man – für alle Zeiten – durch
Ableiten
v (t ) = y& (t ) = − yˆ ω01 ⋅ sin(ω01t )
[dabei ist bereits ϕ0 = 0 gesetzt].
Die Geschwindigkeit am Ort ' C' kann also über die Bestimmung des Zeitpunkts t C ,
an dem der Ort ' C' erreicht wird, bestimmt werden.
Dafür gilt nach dem Auslenkung-Zeit-Gesetz
y C = y 2 = y 1 ⋅ cos(ω01 t C )
damit wird
y
cos( ω01 t C ) = 2 =
y1
=−
−
1
3 ⋅ y1
2
y1
1
3
2
also
( ω01 t C ) = arc cos( −
1
3)
2
5π
6
daraus ergibt sich der Zeitpunkt der Kopplung
(ω01 t C ) =
5π
5π
=
6 ω01 6 ⋅ 6,0 s −1
= 0,463 s
tC =
Diesen Zeitpunkt t C braucht man aber gar nicht explizit auszurechnen; denn im
Argument der Sinus-Funktion im Geschwindigkeit-Zeit-Gesetz tritt ebenfalls nur die
5π
Kombination (ω01t C ) =
auf.
6
Für die Geschwindigkeit des Gleiters am Ort ' C' gilt
v C = y& (t = t C ) = − y 1 ω01 ⋅ sin(ω01 t C )
= − 0,2 m ⋅ 6,0 s −1 ⋅ sin(
5π
1
) = − 0,2 m ⋅ 6,0 s −1 ⋅
6
2
v C = − 0,60 ms −1
Das negative Vorzeichen bedeutet, dass die Bewegungsrichtung im Zeitpunkt des
Zusammenstoßes der als positiv genommenen Richtung der anfänglichen Stauchung
entgegengerichtet ist.
Schwingungslehre
-4-
Prüfungsaufgabe 23
Alternativer Lösungsweg
Ein zweiter Weg zur Bestimmung der Geschwindigkeit des Gleiters am Ort ' C'
benutzt den Satz von der Erhaltung der Energie in seiner Fassung der Mechanik, da
die Schwingungsbewegung reibungsfrei erfolgen soll. Zu jedem Zeitpunkt muss die
Summe aus der potentiellen Energie der Feder und der kinetischen Energie des
bewegten Gleiters gleich der Gesamtenergie des schwingungsfähigen Systems sein.
Die Gesamtenergie des Systems ist aber durch die Stauchung der Feder zu Beginn
des Versuchs eindeutig festgelegt.
Für die potentielle Energie einer gedehnten oder gestauchten Feder gilt allgemein
1
cy2
2
Für die kinetische Energie des bewegten Gleiters gilt
Feder
E pot
=
Gleiter
E kin
=
1
m1 v 2
2
Für die Orte ' C' und ' A ' liefert der Erhaltungssatz der Energie in seiner Fassung der
Mechanik die Identität
Feder
Gleiter
Feder
Gleiter
E pot
(C) + E kin
(C) = E pot
(A) + E kin
(A)
mit
Gleiter
E kin
(A) = 0
Damit lässt sich die kinetische Energie des Gleiters am Ort ' C' ausdrücken als
Gleiter
Feder
Feder
E kin
(C) = E pot
(A) − E pot
(C)
Mit
1
1
N
c y 12 = ⋅ 100 ⋅ (0,20 m) 2
2
2
m
= 2,00 N m
Feder
E pot
(A) =
und
1
1
1
1 3
3 Feder
c y 2 2 = c( −
3 ⋅ y 1 )2 = ⋅ c y 12 = ⋅ E pot
(A)
2
2
2
2 4
4
= 1,50 N m
Feder
Epot
(C) =
wird
1
Feder
Feder
m 1v C 2 = Epot
(A) − E pot
(C) = (2,0 − 1,50) N m
2
= 0,50 N m
Gleiter
Ekin
(C) =
Schwingungslehre
-5-
Prüfungsaufgabe 23
Daraus ergibt sich
v C2 =
2 ⋅ 0,50 N m 9,00 kg m s −2 ⋅ m
=
25
25 kg
kg
9
= 0,36
m2
s2
und
m
s
Weil die Bewegung nach links (in negative Koordinatenrichtung) erfolgt, muss das
negative Vorzeichen gewählt werden.
v C = ( ± ) 0,60
Schwingungslehre
-6-
Prüfungsaufgabe 23
(c) Die Aussage “die Gleiter koppeln beim Stoß“ bedeutet, dass sich beide Gleiter
unmittelbar nach dem Stoß mit gleicher, einheitlicher Geschwindigkeit weiter
bewegen. Damit liegt – nach der Definition – ein vollständig inelastischer Stoß vor.
Da keine äußeren Kräfte in Bewegungsrichtung wirken ändert sich der Impuls des
Systems nicht, es gilt der Satz von der Erhaltung des Impulses.
also
m1v C = ( m1 + m 2 ) u gem
dabei ist u gem die gemeinsame Geschwindigkeit der beiden Gleiter unmittelbar nach
dem Koppeln beim Stoß.
u gem =
m1
⋅vC =
(m1 + m2 )
m1
4
⋅ v C = ⋅ ( − 0,60 m s −1 )
1
5
(m1 + m1 )
4
= − 0,48 m s −1
Die gemeinsame Bewegung ist ebenfalls nach links gerichtet
(in negative Koordinatenrichtung).
Eigenkreisfrequenz ω0 , Eigenfrequenz f0 und Schwingungsdauer T0 ändern sich,
wenn bei ungeänderter Feder(konstante) die Masse des angehängten Körpers
verändert wird. Damit wird
ω02 2 =
c
100 N m −1 3600 kg m s −2 m −1
=
=
1
5 25
125 kg
(m1 + m1 )
⋅
kg
4
4 9
= 28,8 s − 2
und
ω02 = 5,4 s −1
damit wird
2π
2π
=
ω02 5,4 s −1
= 1,17 s
T02 =
Schwingungslehre
-7-
Prüfungsaufgabe 23
Schwingungslehre – Prüfungsaufgabe 24
In einem Messgerät führt eine homogene Metallscheibe (Masse m , Radius
R = 10 cm ) Pendelschwingungen – bei kleinen Winkelausschlägen – um eine Achse
senkrecht zur Scheibenebene durch den Punkt P, aus (vgl. Skizze).
P
A
x
r
g
S
R
Das axiale Massenträgheitsmoment J S der Scheibe bezüglich einer Achse senkrecht
1
zur Scheibenebene durch den Schwerpunkt S ist gegeben durch J S = mR 2 .
2
In einem ersten Versuch schwingt die Scheibe ungedämpft.
(a) Berechnen Sie die Schwingungsdauer T0 und die Eigenkreisfrequenz ω 0 der
Scheibe.
In einem zweiten Versuch lässt man die Scheibe in einem zähen Öl schwingen.
Man beobachtet eine exponentielle Abnahme der Ausschläge und misst bei starker
Dämpfung eine Schwingungsdauer Td , die um 5 % größer ist als T0 .
(b) Bestimmen Sie den Dämpfungsgrad D und den Abklingkoeffizienten δ .
In einem dritten Versuch soll die Scheibe wieder ungedämpft schwingen. Dabei soll
die Drehachse senkrecht zur Scheibenebene durch den Punkt A gehen, der
zwischen Schwerpunkt S und Punkt P liegt (vgl. Skizze).
(c) In welchem Abstand x = xmin müsste man die Achse anbringen, damit die
Schwingungsdauer TA ( x ) am kleinsten wird?
(d) Berechnen Sie TA ( xmin ) .
Schwingungslehre
-1-
Prüfungsaufgabe 24
Schwingungslehre – Prüfungsaufgabe 24 – Kurzlösungen
3
(a) Massenträgheitsmoment (STEINERscher Satz) J P = m R 2 .
2
Eigenkreisfrequenz ω0 = 8,09 s −1 ; Schwingungsdauer T0 = 0,777 s .
(b) Dämpfungsgrad D = 0,305 ; Abklingkoeffizient δ = 2,47 s −1 .
(c) Massenträgheitsmoment Abstand x = AS wird J A =
1
mR 2 + m x 2 .
2
⎛1
2
2⎞
⎜ mR +m x ⎟
4π 2 R 2
2
⎠
2 ⎝2
Schwingungsdauer(Quadrat) T A ( x ) = (2π)
=
⋅(
+ x) .
mg x
g
2x
1
2 R = 7,07 cm .
2
[Der negative Wert der Wurzel ist physikalisch sinnlos].
’Extremum‘ x min =
(d) Schwingungsdauer T A,min = 0,754 s .
Schwingungslehre
-2-
Prüfungsaufgabe 24
Schwingungslehre – Prüfungsaufgabe 24 – Musterlösung
(a) Die Scheibe kann im Schwerefeld der Erde schwingen. Für ein physikalisches
Pendel ist die Eigenkreisfrequenz bei kleinen Auslenkungen aus der Ruhelage
gegeben durch
ω0 2 =
mit m
g
m g d m g (PS )
=
JP
JP
Gesamtmasse
Schwerebeschleunigung
d = PS Abstand zwischen Drehpunkt P und Massenmittelpunkt S
JP
Massenträgheitsmoment bezüglich des Drehpunkts P
Der Schwerpunkt liegt aus Symmetriegründen im Mittelpunkt der Scheibe. Der
Abstand d = PS zwischen Aufhängepunkt P und Schwerpunkt S ist damit gleich dem
Radius R der Scheibe.
Das Massenträgheitsmoment JP bezüglich des Drehpunkts berechnet sich nach
dem STEINERschen Satz zu
1
3
J P = J S + m R 2 = mR 2 + m R 2 = mR 2
2
2
Für die Eigenkreisfrequenz ω 0 erhält man mit den o. g. Werten
ω0 2 =
mg R
mg R
2 g 2 ⋅ 9,81 ms −2
=
=
=
3
JP
3R
3 ⋅ 0,10 m
2
mR
2
= 65,4 s − 2
und
ω0 = 8,09 s −1
Die Schwingungsdauer wird
2π
2π
=
ω0 8,09 s −1
= 0,777 s
T0 =
(b) Die gemessene Schwingungsdauer bei starker Dämpfung ist Td = 1,05 ⋅T0 .
Für die Kreisfrequenz mit Dämpfung ω d gilt die Beziehung
ωd2 = ω0 2 (1 − D 2 )
oder
D =1−
2
Schwingungslehre
ωd 2
ω0 2
-3-
Prüfungsaufgabe 24
daraus wird mit ω0 =
D 2 = (1 −
2π
T0
und
T0 2
1,00 2
Td
1,05 2
) = (1 −
2
ωd =
2π
Td
) = (1 − 0,907 )
= 0,0930
und der Dämpfungsgrad
D = 0,305
Den Abklingkoeffizienten δ erhält man aus der Definition des Dämpfungsgrades D
als Quotient aus Abklingkoeffizient δ und Eigenkreisfrequenz ω0
D=
δ
ω0
zu
δ = D ω0 = 0,305 ⋅ 8,09 s −1
= 2,47 s −1
(c) Für die Schwingungsdauer um den Punkt A gilt, analog zu Teilaufgabe (a), für
das Massenträgheitsmoment für einen Abstand x = AS zwischen Drehachse A und
Massenmittelpunkt S , also für 0 < x ≤ R
1
mR 2 + m x 2
2
Damit gilt für das Quadrat der Schwingungsdauer bei einer Schwingung um A
JA =
⎛1
2
2⎞
⎜ mR +m x ⎟
4π 2 R 2
2
⎠
2 ⎝2
T A ( x ) = ( 2π )
=
⋅(
+ x)
mg x
g
2x
Die Bestimmung der kürzesten Schwingungsdauer in Abhängigkeit von der
Koordinate x des Aufhängepunkts A ist eine Extremwertaufgabe für TA ( x ) bzw.
TA 2 ( x ) ; denn wenn TA ( x ) einen Extremwert hat, dann hat auch TA 2 ( x ) einen
Extremwert.
2
Die erste Ableitung von TA ( x ) ist
d
4π 2 R 2 ( −1)
TA 2 ( x ) =
⋅(
⋅
+ 1)
dx
2 x2
g
Für die Bedingung ’Extremum‘ (physikalisch ohne weitere Mathematik als 'Minimum'
genommen) muss die eckige Klammer gleich null werden, also gilt
R2 1
⋅
=1
2 xmin 2
Schwingungslehre
-4-
Prüfungsaufgabe 24
oder
1
xmin 2 = R 2 .
2
x min =
1
2 R = 7,07 cm [der negative Wert der Wurzel ist physikalisch sinnlos].
2
(d) Die Schwingungsdauer T A,min = T A ( x min ) wird
T A,min 2
1
( m R 2 + m x min 2 )
= ( 2π ) 2 2
mg x min
11
2
1 R
R
= 4π 2 ⋅ ( ⋅ ⋅R 2 ⋅
+ ⋅ ) = 4π 2 2 ⋅
2g
R
g 2
g
= 0,569 s 2
also
T A,min = 0,754 s .
Für mathematische Puristen
Zur Entscheidung ’Minimum’ oder ’Maximum‘ ist das Vorzeichen der zweiten
Ableitung zu bestimmen.
d d
d 4π 2 R 2 ( −1)
4π 2 R 2 ( −1)( −2) 4π 2 R 2
⋅(
⋅ 2 + 1)] =
⋅[
⋅
⋅[ 3 ]
[ TA 2 ( x )] =
[
]=
g
g
dx dx
dx g
2 x
2
x3
x
Da die zweite Ableitung nur positive Größen enthält, wird
4π 2 R 2 1
[TA ( x )] =
⋅ 3 >0
g
dx 2
x
damit ist die hinreichende Bedingung für ein Minimum der Funktion erfüllt.
d2
2
Schwingungslehre
-5-
Prüfungsaufgabe 24
Schwingungslehre – Prüfungsaufgabe 25
Das Massenträgheitsmoment J S eines Rads
(Außen-Radius R = 15 cm ) soll für eine Drehachse
durch den Mittelpunkt S (zugleich aus Symmetriegründen Massenmittelpunkt) experimentell bestimmt
werden.
Dazu wird das Rad auf eine waagrechte Achse gesteckt, so dass sich (idealisiert) reibungsfrei um den
Mittelpunkt S drehen kann. Befestigt man am
Außen-Radius einen – vereinfachend als punktförmig zu behandelnden – Körper (Masse m = 900 g )
dann kann das Rad, nach Auslenkung aus der Ruhelage, ungedämpfte Pendelschwingungen um die
Drehachse durch S ausführen.
S
β
R
m
Die Schwingungsdauer bei kleinen Auslenkungen aus der Ruhelage wurde experimentell aus mehreren Messungen zu T0 = 1,4 s bestimmt.
(a) Bestimmen Sie für kleine Winkelauslenkungen β des schwingungsfähigen Systems aus der Ruhelage den Betrag des rücktreibenden Drehmoments M rück bezüglich des Punktes S auf das System.
(b) Geben Sie einen Ausdruck an für das gesamte Massenträgheitsmoment von Rad
und Punktmasse bezüglich Punkt S .
(c) Stellen Sie die Differentialgleichung der freien ungedämpften Schwingung für
kleine Auslenkungen aus der Ruhelage auf und geben Sie die Eigenkreisfrequenz ω0 und die Schwingungsdauer T0 an.
(d) Berechnen Sie aus der in Teilaufgabe (c) hergeleiteten Beziehung für die
Schwingungsdauer T0 das Massenträgheitsmoment J S des Rades.
Schwingungslehre
-1-
Prüfungsaufgabe 25
Schwingungslehre – Prüfungsaufgabe 25 – Kurzlösungen
(a) Rücktreibendes Drehmoment (linearisiert) M rück = − m g R β .
Massenträgheitsmoment J ges = J S + J K = J S + mR 2 .
&& +
(b) Differentialgleichung β
mg R
JS + m R 2
β = 0.
(c) Beziehung für Eigenkreisfrequenz ω0 2 =
mg R
JS + m R 2
.
JS + m R 2
2π
Schwingungsdauer T0 =
.
= 2π
mg R
ω0
(d) Massenträgheitsmoment J S =
Schwingungslehre
T0 2
4π
2
mgR − mR 2 = 4,55 ⋅ 10 − 2 kg m 2 .
-2-
Prüfungsaufgabe 25
Schwingungslehre – Prüfungsaufgabe 25 – Musterlösung
(a) Wegen der Symmetrie des Rades kann dieses zwar um eine Achse durch den
Massenmittelpunkt S rotieren; das Rad liefert aber keinen Beitrag zu einem
rücktreibenden Drehmoment durch den Massenmittelpunkt. Denken Sie an die
Definition des Massenmittelpunkts.
Ein rücktreibendes Drehmoment wird nur von dem aus der Ruhelage (tiefster Punkt)
ausgelenkten materiellen Körper ausgeübt. Der Betrag ergibt sich zu
M rück = − m g R sin β
Für kleine Auslenkwinkel darf die Sinusfunktion näherungsweise durch den Winkel
(im Bogenmaß) ersetzt werden. Mit
sin β ≈ β
wird das rücktreibende Drehmoment proportional zum Auslenkwinkel
M rück = − m g R β
Diese lineare Abhängigkeit ist die notwendige Voraussetzung für ungedämpfte
harmonische Schwingungen.
(b) Das gesamte Massenträgheitsmoment des Systems J ges (Rad plus materieller
Körper) bezüglich S setzt sich additiv aus zwei Beiträgen zusammen
•
dem Massenträgheitsmoment des Reifens J S ,
•
dem Massenträgheitsmoment des punktförmigen Körpers J K .
Also
J ges = J S + J K = J S + mR 2
(c) Die Grundgleichung für Drehbewegungen nach NEWTON lautet
d 2β
&&
= J ges β
dt 2
Mit den Teilergebnissen von (a) und (b) folgt für diese Differentialgleichung
MRück = J ges
&&
− m g R β = (J M + mR 2 ) β
Damit ergibt sich für die harmonischen Schwingungen die Differentialgleichung
&& +
β
mgR
JS + m R 2
β =0
Koeffizientenvergleich mit der Standard-Differentialgleichung für harmonische
Schwingungen
y&& + ω0 2 y = 0
liefert als Beziehung für die Eigenkreisfrequenz
ω0 2 =
mg R
JS + m R 2
Schwingungslehre
-3-
Prüfungsaufgabe 25
Daraus ergibt sich die Schwingungsdauer des physikalischen Pendels – immer mit
der Einschränkung ’kleine Auslenkungen’ aus der Ruhelage –
T0 =
J + mR2
2π
= 2π S
mg R
ω0
(d) Die in Teilaufgabe (c) hergeleitete Beziehung für die Schwingungsdauer
J S + mR 2
mgR
T0 = 2π
erlaubt es, das Gesamtmassenträgheitsmoment des Rads J S zu bestimmen.
Quadrieren und umstellen liefert
T0
J S + mR 2
= 4π
mgR
2
2
T0 2
4π
2
mgR = J S + mR 2
Daraus erhält man schließlich das Massenträgheitsmoment J S
JS =
=
T0 2
4π
2
mgR − mR 2
(1,4 s) 2
4π
2
⋅ 0,9 kg ⋅ 9,81 m s − 2 ⋅ 1,5 ⋅ 10 −1 m − 0,9 kg ⋅ (1,5 ⋅ 10 −1 m) 2
= 4,55 ⋅ 10 − 2 kg m 2
Schwingungslehre
-4-
Prüfungsaufgabe 25