Determinismus - Physikalisches Institut Heidelberg

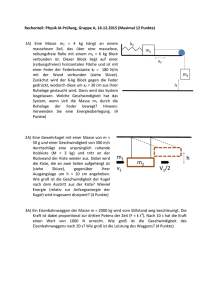
Huygens-Cassini
zum sich
Saturn
und zum Mond Titan
(Huygens-Sonde)
Leitthema:
WieMission
gut lassen
Teilchenbahnen
vorhersagen?
Determinismus, Chaos und Unschärfe
Huygens-Mission Wikipedia
• die präzise Vorhersage von Teilchenbahnen (mechanischer Bewegungen) sind ein
sehr wichtiger Erfolg der Physik insbesondere auch für Anwendungen und Technik
• kennen sie überzeugende Beispiele?
- Huygens-Cassini Mission zum Saturn (.. Jahre)
- Berechnung von Planetenbahnen, Sonnenfinsternissen …
- Bewegung von Jonen in Teilchenbeschleunigern, von Elektronen im Elektronenmikroskop
Fragen:
• sind Teilchenbahnen im Prinzip beliebig genau vorhersagbar, wenn wir alle Kräfte kennen?
• Sind die Gleichungen der Mechanik also ‘deterministisch’? (siehe Zitat von Laplace:
Laplace'scher Daemon )
Zitat Laplace (1749-1827)
„Wir müssen also den gegenwärtigen Zustand des Universums als Folge eines früheren Zustandes
ansehen und als Ursache des Zustandes, der danach kommt. Eine Intelligenz, die in einem gegebenen
Augenblick alle Kräfte kennt, mit denen die Welt begabt ist, und die gegenwärtige Lage der Gebilde,
die sie zusammensetzen, und die überdies umfassend genug wäre, diese Kenntnisse der Analyse zu
unterwerfen,
würde
in der gleichen
Formel
Bewegungen
größten
Himmelskörper
Die
Sonde war
5 Jahre
unterwegs
unddie
wurde
immerder
wieder
beim
Vorbeiflugund
andie
derdes
leichtesten Atoms einbegreifen. Nichts wäre für sie ungewiss, Zukunft und Vergangenheit lägen klar
[1]
vor ihren
Augen.“
Venus,
der
Erde und
am Jupiter beschleunigt.
Bahnkurven im ‘Phasenraum’
Die Frage ob die Bahnen von Massen determiniert sind, wenn wir alle Kräfte kennen, werden
wir diskutieren, indem wir die Newtonschen Bewegungsgleichungen etwas
umformen, so dass wir ein sehr intuitives und anschauliches Bild von ihnen bekommen, und die
Bahnkurven ‘sehen’ können. Wir gehen zur sogenannten ‘Phasenraumdarstellung’ über, bei der
die Bahnkurve in den Variablen Impuls und Ort betrachtet wird (px,x)
(wir beschränken uns der Einfachheit halber auf eine Dimension)
dpx/dt = dpx/dx · dx/dt = dpx/dx · vx = Fx 
m dvx/dt = 1/vx Fx(x,vx)
DGl. für die Bahnkurve in (px,x)
Das ist die Bewegungsgleichung (DGl 1.O) für die Bahnkurve im Phasenraum.
Wir können damit an jedem Punkt im Phasenraum die Steigung der Bahnkurve
berechnen.
Das lässt sich graphisch als Steigungfeld darstellen!
Steigungsfeld
Beispiel:‘Sinuspendel’ (physikalisches Pendel)
(kann auch Überschläge machen)
1

s
φ
L
m
Fs

2
s=L·φ
F=mg
m ds/dt = Fs = - mg sin (φ)
ds/ds = - g sin( s/L)/s
Bewegungsgleichung im Phasenraum
s
1.Wir wählen einen Startpunkt im Phasenraum
d.h. wir legen s0 und s0 fest z.B. Punkt 1 oder 2
2. Die Steigung an diesem Punkt zeigt uns die
Richtung, in welche das Teilchen sich bewegt
-angezeigt durch den roten Pfeil. So wandern
wir in kleinen Schritten durchs Steigungsfeld.

s

1

3
x
x

2
s
Ins Steigungsfeld wurden (von Hand) 3 Bahnkurven eingezeichnet, die von den Startpunkten
1,2 und 3 ausgehen und die sich ‘in das Steigungsfeld schmiegen’.
Bahnkurven 1 und 3: Die Masse startet mit hoher Geschwindigkeit von der Ruhelage des Pendels
Der Weg nimmt unbegrenzt zu, wobei die Geschwindigkeit sich periodisch
ändert! Hier macht das Pendel Überschläge
Bei Bahn 3 schafft sie den Überschlag gerade so. Bei den Punkten
x bliebe die Masse im instabilen Gleichgewicht senkrecht nach oben stehen.
Bahnkurve 2: Hier startet die Masse mit grossem Ausschlag und kleiner Geschwindigkeit.
Die Energie reicht nicht zu einem Überschlag – die Masse macht eine nicht
harmonische Schwingung. Es wird immer wieder die gleiche Bahnkurve durchlaufen.
 + γ * s (z.B. Luftreibung)
Fadenpendel mit Dämpfung: Reibungskraft F = -mg sin(φ)
s

s
Hier startet die Masse mit hoher Geschwindigkeit, so dass das Pendel sich überschlägt.
Sie verliert aber durch die Reibungsarbeit kontinuierlich Energie, so dass es nicht mehr für
einen dritten Überschlag reicht  das Pendel macht jetzt eine gedämpfte Schwingung.
Wenn der Punkt im Phasenraum zu einem Zeitpunkt festgelegt ist und alle Kräfte bekannt
sind, kann die Bahnkurve im Prinzip beliebig genau für beliebig lange Zeiten berechnet
werden. Die Bewegungsgleichung der Mechanik ist also deterministisch!
Hinweis: Unser Verfahren zur Lösung heisst ‘numerische Integration’. Dabei treten natürlich
Integrationsfehler auf, die aber mit schlauen Algorithmen und viel Rechenleistung beliebig
klein gemacht werden können. Das ist ein Problem der angewandten Mathermatik, nicht
der Physik.
Der Nutzen von Näherungen und von analytischen vollständigen Lösungen
In den Grundvorlesungen werden numerische Lösungen im Phasenraum i.A. nicht diskutiert.
Statt dessen werden Schwingungen als Lösungen für Kräfte diskutiert, die rücktreibend sind
und linear mit der Amplitude anwachsen: m dx/dt = - k*x
Diese Differentialgleichung lässt sich analytisch lösen: x(t) = A* sin(2πf t + α) und enthält alle
Lösungen.
Auch unser Fadenpendel macht in guter Näherung harmonische Schwingungen für
kleine Ausschläge, d.h s << L  φ << 1. Dann gilt sin(s/L) ≈ s/L (Taylor-Entwicklung)

- g sin( s/L) ≈ - g/L s /s= ds/dt
Fadenpendel für kleine Auslenkungen
( Die Bahnkurven im PR sind Ellipsen)
Warum machen wir solche Näherungen?
•
eine analytische Lösung erlaubt es, allgemeine Aussagen über Schwingungen zu machen
wie z.B. Energiebilanz, Aufteileung der Energie zw. Kinetischer und potentieller Energie,…
Harmonische Schwingungen sind das exemplarische Beispiel für eine Schwingung.
• Alle periodischen Bewegungen, also auch nichtlineare Schwingungen, lassen sich als Summe
von harmonischen Schwingungen mit der Grundfrequenz f und deren Vielfachen darstellen,
wobei die einzelnen Beiträge in der Summe unterscheidliche Amplituden und Phasen haben.
Mathematisch ist das die ‘Fourierreihe’: s(t)= Σ An sin (2π nf t + αn)
(n = 0 .. )
n
•
Nichtlineare Schwingungen haben also ein Frequenzspektrum, das die Grundfrequenz und
Vielfache davon enthält!
Hinweis: das gilt nicht nur für Schwingungen sondern auch für periodische Wellen  Akustik
(Obertöne) und elektromagnetische Wellen
Grenzen des Determinismus: deterministisches Chaos und Unschärferelation
Die Voraussetzung des Determinismus war, dass wir alle Kräfte beliebig genau kennen und die
Anfangsbedingungen beliebig genau festlegen können.
Hier gibt es wichtige praktische und grundsätzliche Grenzen
1.
Wir können nicht alle Kräfte beliebig gut kennen, kleine Störungen einer Teilchenbahn
z.B. durch die Umwelt sind unvermeidbar. Wenn die Differentialgleichung so beschaffen ist,
dass es im Phasenraum Bereiche gibt, an denen die Steigungsfelder sich ‘verzweigen’ *),
so dass zwei sehr eng benachbarte Punkte im Phasenraum zu ganz unterschiedlichen
Bahnen führen, dann reichen winzige Störungen, um eine Voraussage unmöglich zu
machen. Solche mechanischen Systeme nennt man chaotisch und es gibt sehr viele davon!
2.
Prinzipiell gilt immer die Quantenmechanik! Dort gilt als Grundprinzip die
Heisenbergsche Unschärferelation.
Für unser Fadenpendel heisst das : Δps * Δs  h , h = Plancksches Wirkunsquantum
Diese Relation legt fest, dass wir innerhalb eine Fläche der Grösse h im Phasenraum
prinzipiell nicht wissen können, wo die Masse sich befindet! Also können wir z.B.
auch den Startpunkt prinzipiell nicht genauer bestimmen!
Ob das eine Rolle spielt, hängt allein davon ab, ob unsere ‘Teilchenbahn’ im Phasenraum
einen Bereich einnimmt, dessen Fläche sehr gross gegen h ist, oder in der Grössenordnung von
h liegt! Nur im ersten Fall macht das Konzept von Teilchenbahnen überhaupt Sinn.
*)
Ein triviales Beispiel sind die instabilen Gleichgewichtspunkte unseres Pendels.. Es wird nach links oder rechts fallen!
Einige Informationen zu chaotischen Systemen
• Poincaré machte 1889 die Entdeckung, dass es mechanische Systeme gibt, für welche die
Teilchenbahnen nicht für beliebig lange Zeiten vorhersagbar sind als
er versuchte, Systeme mit 3 Massen unter Gravitationsanziehung zu lösen. Diese Systeme sind
im Normalfall immer chaotisch!
Warum folgen unsere Planeten dann regulären Bahnen um die Sonne, obwohl sie sich ja
auch gegenseitig anziehen? Der Effekt des Jupiter auf die Bahn des Neptun oder die des Neptun
Auf Pluto sind z.B. ziemlich gross!
Antwort1: nicht alle Bahnen sind regulär, die von Pluto ist definitiv chaotisch, d.h. wir wissen
nicht wo Pluto in 20 Millionen Jahren sein wird! Inzwischen weiss man, dass
auch die inneren Planeten chaotisches Verhalten zeigen auf Zeitskalen von einigen
Millionen Jahren.
Antwort2: Es ist ein Wunder! Die Radien der Planetenbahnen zeigen ja eine merkwürdige
unverstandene Gesetzmässigkeit (Titus-Bode Gesetz). Es gibt die starke Vermutung,
die aber nicht bewiesen ist, dass nur diese Bahnen regulär sein können, alle andere
instabil wären. Ähnlich könnte es bei den Saturnringen sein, bei denen es viele Radienbereiche gibt, auf denen keine Gesteinsbrocken gefunden werden! Aufruhr im Sonnensystem
Chaotische Systeme enthalten oft mehrere Massen oder Kraftzentren. Zur Vorführung im Umterricht
eignet sich besonders gut ein gedämpftes 2-d Pendel mit Eisenmasse, die von 3 symmetrisch
angeordneten Magnetenangezogen wird (siehe Anhang). Für grosse Bereiche möglicher
Anfangsbedingungen ist es nicht vorhersagbar bei welchem Magnet das Pendel enden wird!
Illustration zu ‘verboteNenen’ Bahnen’
Ringe des Saturn, aufgenommen aus der ISS Raumstation. Sie werden von Gesteinsbrocken und
Staub verursacht, die um Saturn kreisen. Das helle Bild des Planeten in der Mitte
selbst wurde gelöscht, damit die Ringe besser sichtbar sind.
Die eigentliche Frage ist: Warum gibt es Radienbereiche, die komplett leer sind?
Abb: Phasenraum für ein MehrKörperproblem:
Bahnkurven im (3-D)
Phasenraum für einen Stern im
Gravitationsfeld einer Galaxie
chaotische Bewegung von Sternen
Die geschlossenen Bahnkurven entSprechen regulären periodischen
Bewegungen. Im Phasenraum dominieren aber Gebiete die zu
chaotischen Bahnen gehören.
Hinweis: Chaotische Eigenschaften haben die meisten komplexen Systeme, die durch Differentialgleichungen beschrieben werden wie z.B. das Wetter oder das Klimasystem.
Daher kann z.B. das Wetter prinzipiell immer nur für relativ kurze Zeit vorhergesagt werden, egal
wie gross die Rechenleistung ist oder wie vollständig die Startinformationen sind.
Die Empfindlichkeit des Systems Wetter hat Edward Lorenz sehr drastisch ausgedrückt:
“Doss the flap of a butterfly's wing in Brazil set off a tornado in Texas? “
Dieser “Schmetterlingseffekt” wird oft zitiert und ist berühmt.
Spielwiese: Ein applet mit dem sie ein chaotisches Pendel simulieren können
finden sie unter: Simulation chaotisches Pendel
Dies ist dasselbe Sinuspendel, wie wir es oben benutzt hatten, dessen Aufhängung jetzt aber horizontal von einer äusseren Kraft mit Frequenz omega und Amplitude A periodisch getrieben wird.
Wählbar sind A, die Dämpfung λ und die Frequenz omega.
φ·
φ·
φ
Bei diesen Einstellungen gibt es nach einiger
Zeit eine periodische nicht harmonische
Schwingung (verbeulte Ellipse)
φ
Bei dieser Einstellung ist die Bahn chaotisch.
(keine Wiederholung derselben Bahnen)
 φ) gezeigt )
(Links unten sind jeweils die Bahnkurven im Phasenraum (φ,
Unschärferelation der Quantenmechanik
Als erstes Beispiel nehmen wir das Wasserstoffmolekül als Beispiel eines Oszillators:
Die Potentielle Energie als Funktion des Abstandes R der beiden Protonen hat ein
Minimum  Die beiden Protonen können gegeneinander schwingen.
Die Abschätzung ergibt, dass für
Schwingungen des Moleküls ungefähr gilt:
ΔR* Δp ≈ 1.3 10-33 Js ≈ 2 h
R = 0.74* 10-10 m
p
p
Die Fläche der Schwingung im Phasenraum
ist also vergleichbar mit dem Planckschen
Wirkungsquantum. Hier macht es keinen Sinn
von einer klassischen Teilchenbahn zu reden!
Hier brauchen wir die Quantenmechanik.
4.5 eV
1. Schwingung
Zur Abschätzung nehmen wir:
ΔR = 0.74 10-10 m
<Ekin> =
p2/2mp =
0.74 Å
0.65 eV (erster Vibr.Zustand)
Daraus Δp ≈ p = sqrt(0.65 eV* 2 mp)
= 1.8 10-23 Js/m
ΔR* Δp ≈ 1.3 10-33 Js ≈ 2 h
Experimentell gemessene Energieabstände der Schwingungsmoden von H2
ΔE = hν0 = 1.3 eV
<Ekin> = 1.3/2 eV = 0.65 eV
2. Beispiel: Elektron im homogenen Magnetfeld: Fadenstrahlrohr
Energie der
Elektronen:
Ekin =e*U
R
In diesem Schulversuch sieht man die Kreisbahn der Elektronen, weil sie Restgasmoleküle zum Leuchten bringen.
Für Elektronen in Atomen gibt es keine ‘Teilchenbahnen, wir sehen sie aber im Fadenstrahlrohr
oder in der Braunschen Röhre (Oszillograph, Röhrenfernseher): warum?
Typische Werte: R= 7 cm; U = 265 V  Ekin = 265 eV =( 4.246.004)* 10-17 J (Ungenauigkeit der
Spannung)
 Δpx = Δpy = sqrt (2 me * ΔEkin) = 2.8 10-27 Js/m
Aus der Unschärferelation folgt dann: ΔR ≈ h/ Δp ≈ 2.4 10-9 m << R
Die aus der Quantenmechanik folgende Umschärfe liegt hier im Bereich eines
Atomdurchmessers – vollkommen irrelevant für dieses Experiment.
Die klassische Teilchenbahn ist hier eine exzellente Näherung, wir können die
klassische Mechanik nutzen, um die Bahn auszurechnen!
Anhang: Chaotisches Pendel mit 3 Magneten
Dieser Aufbau eignet sich sehr gut zur Vorführung in einem Kurs/ einer Übungsgruppe
Chaotisches Pendel mit 3 Magneten
Video einer chaotischen Bahn: zum Start in das Bild
Klicken.
Die Farben der Startorte geben an
bei welchem Magneten die Bahn endet
Magnetpositionen