Logarithmen

math_ges_soz11_log_april2014.nb
1
11. Logarithmen
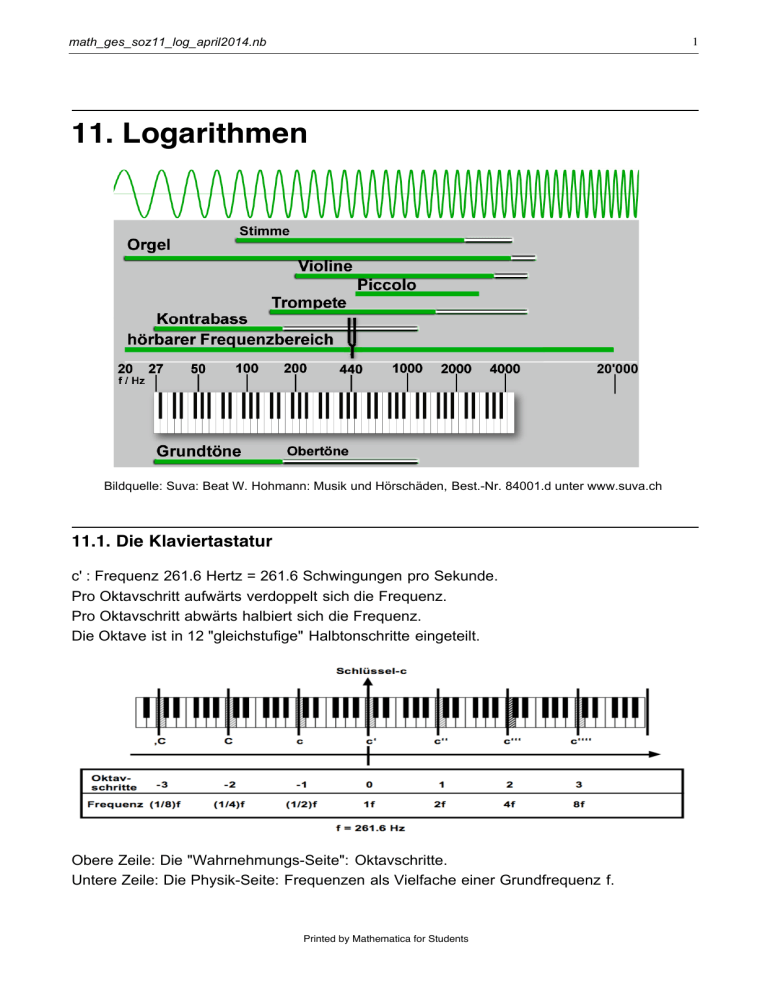
Bildquelle: Suva: Beat W. Hohmann: Musik und Hörschäden, Best.-Nr. 84001.d unter www.suva.ch
11.1. Die Klaviertastatur
c' : Frequenz 261.6 Hertz = 261.6 Schwingungen pro Sekunde.
Pro Oktavschritt aufwärts verdoppelt sich die Frequenz.
Pro Oktavschritt abwärts halbiert sich die Frequenz.
Die Oktave ist in 12 "gleichstufige" Halbtonschritte eingeteilt.
Obere Zeile: Die "Wahrnehmungs-Seite": Oktavschritte.
Untere Zeile: Die Physik-Seite: Frequenzen als Vielfache einer Grundfrequenz f.
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
2
11.2. Erkenntnisse
1. Die obere Zeile ist additiv, die untere multiplikativ: +1 oben entspricht •2 unten.
2. Einer Multiplikation unten (Bsp: 2•4 = 8) entspricht eine Addition oben (Bsp: 1+2 = 3).
Einer Division unten (8:4 = 2) entspricht eine Subtraktion oben (3-1 = 2).
3. Die Oktavschritt-Zahlen sind die Exponenten zur Basis 2 der Frequenzzahlen unten.
Diese Exponenten heissen Zweierlogarithmen der Frequenzzahlen unten.
Oktav-Nr.
-2
-1
0
1
2
3
4
5
6
1
1
Logarithmen
log2 I ÄÄÄÄ
M log2 I ÄÄÄÄ
M log2 H1L log2 H2L log2 H4L log2 H8L log2 H16L log2 H32L log2 H64L
4
2
("rote Zahlen")
log(4) + log(8)
= log(4•8)
-------------------------------------------------------------------------------------------------------------------Frequenz als
1
1
Vielfaches einer
ÅÅÅÅ
ÅÅÅÅ
1
2
4
8
16
32
64
4
2
Grundfrequenz f
Numeri ("schwarze 2-2
2-1
20
21
22
23
24
25
26
Zahlen")
Die Logarithmen sind eine schweizerisch-schottische Co-Erfindung. Etwa gleichzeitig, um
ca. 1600, konstruierten der Toggenburger Uhrmacher Jost Bürgi und der Schotte John
Napier Logarithmentabellen mit dem Ziel, Multiplikationen durch Additionen und Divisionen
durch Subtraktionen zu ersetzen. Dies wurde nötig, da mit der Erfindung des Fernrohrs um
1600 komplizierte Planetenrechnungen durchgeführt wurden.
Auch heute, im Computerzeitalter, verwandeln Logarithmen beim Berechnen eines
Computertomogramms komplizierte multiplikative Gleichungen in gewöhnliche additive
Gleichungssysteme (ca. eine halbe Million Gleichungen mit einer halben Million
Unbekannten pro Tomogramm); ohne diese logarithmische Umformung könnte selbst ein
moderner Computer kein Tomogramm berechnen. Unsere CT-Technik funktioniert also nur
dank der Erfindung der Logarithmen.
Jost Bürgi scheint die Idee zu Logarithmentabellen etwas vor John Napier entwickelt zu
haben. Bürgi stammte jedoch aus einer sehr einfachen Familie aus Lichtensteig bei Wattwil
und genoss nie eine offizielle mathematische Ausbildung; er war reiner Autodidakt. John
Napier dagegen stammte aus einer gebildeten schottischen Familie und erfuhr
entsprechende fachliche Schulung. So kam es, dass meist John Napier als Erfinder der
Logarithmen ins Zentrum gerückt wird. Johannes Kepler verwendete für seine
Planetenberechnungen sowohl Tabellen von Bürgi wie von Napier.
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
3
11.3. Die "Frage nach dem Logarithmus" und die Logarithmengesetze
Logarithmen kann man zu jeder Basis > 0 bilden.
Aufgabe in Worten
In Kurzform
Zweierlog von 4
log2 (4) = x
Als Exponentialgleichung
("Frage nach dem Log.")
2x = 4
Lösung: x =
log2 (4) =
Zweierlog von 8
Zweierlog von 1/2
Zweierlog von 0.25
Zweierlog von 1
Zweierlog von -1
Wir merken: Negative Numeri und die Null haben keinen Logarithmus.
Zusammenfassung
Die Exponenten der Zahl z zur festgewählten Basis a heissen Logarithmen von z zur
Basis a. Abgekürzt: loga (z). Beispiele:
x = log10 H5L (sprich: "Zehnerlogarithmus von 5") bedeutet:
10 x = 5
x = log2 H7L (sprich: "Zweierlogarithmus von 7") bedeutet:
2x = 7
Abkürzungen für spezielle Basen:
Basis 10:
Basis 2:
Basis e:
lg(z)
lb(z)
ln(z)
(auf dem TR: Taste "log")
"logarithmus binarius"
"logarithmus naturalis": wichtig für später!
e ist die Eulersche Zahl, e ≈ 2.7 1828 1828... Die Basis e taucht in Natur-Prozessen (bei fortlaufender
"Verzinsung" / Vermehrung) auf. e ist irrational.
loga HzL = x õ
x als Logarithmus dargestellt:
x als Exponent dargestellt:
Printed by Mathematica for Students
x
a =z
math_ges_soz11_log_april2014.nb
4
loga HzL = x õ
x als Logarithmus dargestellt:


x als Exponent dargestellt:
x
a =z


Basis Numerus Logarithmus


Basis Log. Numerus
NUMERUS = BASISLOGARITHMUS
Die Logarithmengesetze
log(a•b) = log(a) + log(b)
oder umgekehrt:
log(a) + log(b) = log(a•b)
log(a ÷ b) = log(a) - log(b)
oder umgekehrt:
log(a) - log(b) = log(a ÷ b)
Der Logarithmus eines Produkts ist die Summe der Einzellogarithmen.
Der Logarithmus eines Quotients ist die Differenz der Einzellogarithmen.
log(an ) = n•log(a)
oder umgekehrt:
n•log(a) = log(an )
("Sprungregel")
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
5
Aufgaben:
1. Komprimieren Sie in einen einzigen Logarithmus:
1
log(2) + log(8); log(a) + log(b) + log(c); log( ÅÅÅÅ
) + log(4); log(a) + log( ÅÅÅÅ1b );
2
log(a) + log(a) + log(a); lg(4) + lg(25); lg(50) + lg(20); log(x) + log(2x)
2. Komprimieren Sie in einen einzigen Logarithmus:
log(a) + log(b) - log(c); log(a) - log(b) - log(c); log(x 2 ) - log(x); lg(50) - lg(5)
5
3
è!!!
è!!!
è!!!!!
!
1
log(x 3 ); log( x ); log( x ); log( x 5 ; log( ÅÅÅÅ1x ); log( ÅÅÅÅÅÅ
Å)
x2
3. Ziehen Sie die Potenzen aus dem Logarithmus heraus:
4. Komprimieren sie in einen einzigen Logarithmus:
2
3 log(x); 0.5 log(z); ÅÅÅÅ
log(y); - log(z); 2 log(x) + log(y) - 0.5 log(z)
3
Lösungen:
a
1. log(16); log(abc); log(0.5•4) = log(2); log(a• ÅÅÅÅ1b ) = log( ÅÅÅÅ
)
b
log(a•a•a) = log(a3 ); lg(100) = 2; lg(1000) = 3; log(x•2x) = log(2x 2 )
2
ab
a
x
2. log( ÅÅÅÅÅÅ
Å ); log( ÅÅÅÅÅÅ
Å ); log( ÅÅÅÅÅÅ
Å ) = log(x); lg(10) = 1
c
bc
x
1
1
1
5
3. 3 log(x); log(x ÅÅÅÅ2 ) = ÅÅÅÅ12 log(x); log(x ÅÅÅÅ5 ) = ÅÅÅÅ
log(x); ÅÅÅÅ
log(x);
5
3
-1
-2
log(x ) = -1log(x); log(x ) = -2 log(x)
1
2
è!!!
è!!!!!
!
3
1
4. log(x 3 ); log(z ÅÅÅÅ2 ) = log( z ); log(y ÅÅÅÅ3 ) = log( y 2 ; log(z-1 ) = log( ÅÅÅÅ
);
z
2
1
è!!!
x y
log(x 2 ) + log(y) - log(z ÅÅÅÅ2 ) = log(x 2 ) + log(y) - log( z ) = log( ÅÅÅÅÅÅÅÅ
è!!!ÅÅ )
z
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
6
11.4. Exponentialgleichungen lösen mit Hilfe der "Sprungregel"
2x = 3
| lg( ) Wir logarithmieren beide Seiten z.B. mit "lg"
x
lg(2 ) = lg(3)
| Sprungregel anwenden
x lg(2) = lg(3)
| : lg(2)
lgH3L
x = ÅÅÅÅÅÅÅÅ
ÅÅÅ ≈ 1.58496...
lgH2L
Beispiel: Lösen Sie folgende Exponentialgleichung nach x auf:
5'000 = 10'000 • 0.95x
Lösung:
5'000 = 10'000 • 0.95x
0.5 = 0.95x
lg(0.5) = x • lg(0.95)
lgH0.5L
ÄÄÄÄÄÄÄÄ
ÄÄÄÄÄÄÄÄÄÄ = x ≈ 13.5...
lgH0.95L
| : 10'000
| lg (oder ln) und Sprungregel
| : lg(0.95)
Merke: Exponentialgleichungen löst man durch Logarithmieren.
lg(10) = 1;
loga (a) = 1
loga (1) = 0
1
log ( ÅÅÅÅ
) = - log (x)
x
è!!!
1
log( x ) = ÅÅÅÅ
•log(x)
2
3
è!!!
1
log( x ) = ÅÅÅÅ
•log(x)
3
Wichtig: Die Numeri müssen stets > 0 sein! Für negative Zahlen und für die Null
sind keine Logarithmen definiert!
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
7
11.5. Logarithmengleichungen lösen, Scheinlösungen aussondern
Beispiel: Bestimmen Sie die Lösungsmenge folgender Gleichung:
lg(x) = 2 - lg(x - 21)
Lösung:
lg(x) = 2 - lg(x - 21)
| sortieren
lg(x) + lg(x - 21) = 2
| in einen einzigen Logarithmus komprimieren
lg10 [ x(x - 21) ] = 2
| Entlogarithmieren, d.h. als Exponentialgleichung schreiben
2
10 = x(x - 21)
| Grundform dieser quadratischen Gl. herstellen
2
x - 21x - 100 = 0
| faktorisieren, Scheinlösungen aussondern
(x - 25)(x + 4) = 0, x1 = 25, x2 = -4, -4 ist Scheinlösung.  = { 25 }.
11.6. Weitere Übungen
1. Bestimmen Sie folgende Logarithmen exakt:
a) log2 (4)
b) log2 (2)
c) log2 ( ÅÅÅÅ12 )
d) log2 (0.25)
3
5
è!!!!
è!!!
!
è!!!!!
!
1
e) log2 ( 2 ) f) log2 ( ÅÅÅÅÅÅÅÅÅ
g) log2 ( 2 ) h) log2 ( 23 )
è!!!!Å )
i) log2 (
1
ÅÅÅÅÅÅÅÅ
è!!!!!3Å!Å )
5
m) ln( ÅÅÅÅ1e )
2
2
j) log3 ( ÅÅÅÅ19 )
1
k) log5 ( ÅÅÅÅÅÅÅÅÅ
è!!!! Å )
5
l) ln (e2 )
1
n) ln( ÅÅÅÅÅÅ
Å)
e2
2. Komprimieren Sie in einen einzigen Logarithmus:
1
a) ÅÅÅÅ13 log(a2 ) + ÅÅÅÅ
log(b) - log(c)
2
b) lg(x + 1) + lg(x) -3• lg(2)
c) log2 (2x + 1) - log2 (x) - log2 (20)
3. Lösen Sie die Exponentialgleichungen exakt, d.h. mittels Logarithmen:
a) 10 - 52 x + 1 = 8.
b) 22 x + 1 = 20• 2x Tipp: | : 2x
10
c) 2x + 1 - ÅÅÅÅÅÅ
Å = 0 Tipp: | • 2x
2x
600
d) 4x + 1 - ÅÅÅÅÅÅÅÅÅ
Å =0
2x
e) schwierig: 9x - 1 •22 x - 1 = 23 x - 1 • 3x -2 • 5.
Tipps: 9 = 32 . Dann nach Basis sortieren.
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
Lösungen:
1a) 2 b) 1
1
j) -2
k) - ÅÅÅÅ
2
c) -1
l) 2
2
d) -2
m) -1
1
8
e) ÅÅÅÅ12
n) -2
1
f) - ÅÅÅÅ
2
g) ÅÅÅÅ13
h) ÅÅÅÅ35
3
i) - ÅÅÅÅ
5
3
è!!!!!!
2 è!!!!
a
b
2a) = log(a ÅÅÅÅ3 ) + log(b ÅÅÅÅ2 ) - log(c) = log( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ )
c
Hx + 1L x
2x +1
b) lg( ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ
c) log2 ( ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ )
lgH8L
20 x
3a) | -8, + 52 x + 1 ï 2 = 52 x + 1 | lg ï lg(2) = (2x + 1) lg(5) ï
lgH2L
lgH2L
lgH2L
2x + 1 = ÅÅÅÅÅÅÅÅ
ÅÅ ï 2x = ÅÅÅÅÅÅÅÅ
ÅÅ -1 ï x = ÅÅÅÅ12 [ ÅÅÅÅÅÅÅÅ
ÅÅ -1]
lgH5L
lgH5L
lgH5L
lgH0.4L
Variante: 2 = 52 x + 1 | : 5 ï ÅÅÅÅ25 = 0.4 = 52 x = 25x ï x = ÄÄÄÄÄÄÄÄ
ÄÄÄÄÄÄÄÄ
lgH25L
2x+1
lgH20L
2
b) ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = 20 ï 2x + 1 = 20, (x + 1) lg(2) = lg(20), x + 1 = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ ,
2x
lgH2L
lgH20L
x = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ - 1
lgH2L
lgH10L
1
Variante: 2x + 1 = 20 | : 2 ï 2x = 10 ï x = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = ÄÄÄÄÄÄÄÄ
ÄÄÄÄ
lgH2L
lgH2L
c) 22 x + 1 - 10 = 0, 22 x + 1 = 10, (2x + 1) lg(2) = lg(10) = 1 ï
1
1
1
2x + 1 = ÅÅÅÅÅÅÅÅ
ÅÅ ï 2x = ÅÅÅÅÅÅÅÅ
ÅÅ - 1 ï x = ÅÅÅÅ12 [ ÅÅÅÅÅÅÅÅ
ÅÅÅ - 1]
lgH2L
lgH2L
lgH2L
lgH5L
Variante: 22 x + 1 = 10 | : 2 ï 22 x = 5, 4x = 5 ï x = ÄÄÄÄÄÄÄÄ
ÄÄÄÄ
lgH4L
600
600
600
d) = H22 L
- ÅÅÅÅÅÅÅÅÅ
Å = 22 x + 2 - ÅÅÅÅÅÅÅÅÅ
Å = 0 ï 22 x + 2 = ÅÅÅÅÅÅÅÅÅ
Å | •2x ï
2x
2x
2x
lgH600L
23 x + 2 = 600 ï (3x + 2) lg(2) = lg(600) ï 3x + 2 = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ ï
lgH2L
x+1
1 lgH600L
x = ÅÅÅÅ
[ ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ - 2]
3
lgH2L
lgH150L
Variante: 23 x + 2 = 600 | : 4 ï 23 x = 150 ï 8x = 150 ï x = ÄÄÄÄÄÄÄÄ
ÄÄÄÄÄÄÄÄÄ
lgH8L
e) H32 L
•22 x - 1 = 23 x - 1 • 3x -2 •5 ï 32 x - 2 •22 x - 1 = 23 x - 1 • 3x -2 •5 ï
lgH5L
3x
3 x
3x = 2x •5 ï ÅÅÅÅÅÅ
Å
=
5
ï
H
ÅÅÅÅ
L = 5 ï x lg(1.5) = lg(5) ï x = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ
x
2
2
lgH1.5L
x-1
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
9
11.7. Probetest Logarithmen
1. Berechnen Sie x:
a) log5 (x) = -1
1
d) log2 ( ÅÅÅÅ
ÅÅÅÅ!Å ) = x
è!!!
8
1
b) log2 ( ÅÅÅÅÅÅ
Å) = x
16
f) loga (
e) logx 64 = 6
3
"######
1
ÅÅÅÅÅÅ
)
a2
=x
2. Fassen Sie zu einem einzigen Logarithmus zusammen und vereinfachen
1
Sie so stark wie möglich: ÅÅÅÅ
lg(16) + lg(25) - lg( ÅÅÅÅ12 ) + 5•lg(100)
4
3. Gesucht ist die Lösung x. Drücken Sie das Resultat mittels
Zehnerlogarithmen aus:
a) 2x = 5•3x
b) 3x+1 = 20 - 3x
4. Lösen Sie die Exponentialgleichung:
1
128•H ÅÅÅÅ
L
2
3 x-2
= 2x
5. Lösen Sie exakt, d.h. mit Hilfe von lg: 3x + 2 + 7x = 7x + 1 + 3x .
6. Berechnen Sie ohne Rechner:
4
è!!!!!!
a) x = lg( 10 )
b) x = log5 (0.2)
è!!!!
c) x = log2 ( 2 )
5
d) x = log5 ( ÅÅÅÅÅÅÅÅÅ
è!!!!Å )
3
5
7. Berechnen Sie x mit Hilfe von lg: x = log3 (11)
Tipp: Zuerst Exponentialgleichung erzeugen ("Pfeilschema")
8. Lösen Sie die Exponentialgleichung:
a) 3•43 x - 3 = 3•8x
b) 256•0.55 x-4 = 2x
9. Bestimmen Sie x exakt bzw. mit Hilfe von lg:
a) 16810 - 7x + 1 = 3.
b) 22 x + 2 = 65•2x
Printed by Mathematica for Students
c) 3x - 7 = 9x + 4
math_ges_soz11_log_april2014.nb
Lösungen:
1a) 1/5
2. 12
b) -4
10
d) -3/2
3a)
2x = 5•3x | : 3x
lgH5L
x lg( ÅÅÅÅ23 ) = lg(5) ï x = ÅÅÅÅÅÅÅÅ
2ÅÅÅÅÅ
e) 2
f) -2/3
2
ÅÅÅÅÅÅ
Å = 5 ï H ÅÅÅÅ23 L = 5
3x
x
x
ï
lgH ÅÅÅÅ
3L
| lg
3b)
3x+1 + 3x = 20 ï 3x (31 + 1) = 20 ï 3x •4 = 20
lgH5L
ï 3x = 5
ï x lg(3) = lg(5)
ï x = ÅÅÅÅÅÅÅÅ
ÅÅ
lgH3L
4. 9/4
5. 3x+2 - 3x = 7x+1 - 7x ï 3x (32 - 1) = 7x (71 - 1) ï 3x •8 = 7x •6
7
4
ï ÅÅÅÅ86 = ÅÅÅÅÅÅ
Å ï ÅÅÅÅ43 = H ÅÅÅÅ73 L = lg( ÅÅÅÅ
) = x lg( ÅÅÅÅ73 ) ï x = ÅÅÅÅÅÅÅÅ37ÅÅÅÅÅ
3x
3
4
lgH ÅÅÅÅ
L
x
x
lgH ÅÅÅÅ
3L
3
lgH ÅÅÅÅ
4L
lgH ÅÅÅÅ
7L
(oder auch richtig: x = ÅÅÅÅÅÅÅÅ3ÅÅÅÅÅ )
6a) 1/4
b) -1
c) 1/2
d) 2/3
lgH11L
7. 3x = 11 | lg ï x lg(3) = lg(11) ï x = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ
lgH3L
8a) kürzen mit 3 ï H22 L
3x -3
b) 27 H2-1 L
5x-4
c) 3x - 7 = H32 L
= H23 L ï 26 x - 6 = 23 x ï 6x - 6 = 3x ï x = 2
x
= 2x ï 2-5 x + 4 = 2x ï -5x + 5 = x ï 6x = 5 ï x = ÅÅÅÅ56
x+4
ï 3x - 7 = 32 x + 8 ï 3x - 7 = 2x + 8 ï x = 15
9a) 16807 = 7x+1 , 75 = 7x+1 , 5 = x+1, x = 4.
lgH16.25L
22 x+2
b) | : 2x ï ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ = 2x+2 = 65 | : 22 ï 2x = 16.25 ï x = ÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄ
ÄÄÄÄÄÄ
2x
lgH2L
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
11
11.8. Das Weber-Fechnersche Gesetz der Wahrnehmung
"Ein Thaler hat viel weniger Wert für den Reichen als für den Armen, und wenn er einen
Bettler einen Tag lang glücklich macht, so wird er als Zuwachs zum Vermögen eines
Millionärs gar nicht merklich von diesem gespürt."
Gustav Theodor Fechner, 1801 - 1887
Stellen Sie sich vor, Sie sitzen in einer vollkommen dunklen Höhle. Nun wird ein kleines
Kerzenlicht angezündet. Die Wirkung ist riesig: Sie empfinden die Höhle plötzlich als hell
erleuchtet. - Stellen Sie sich nun einen hell erleuchteten Saal vor. Nun entzündet man vor
Ihnen eine Kerze. Sie werden kaum eine Wirkung bemerken, obwohl die neu
hinzukommende Lichtenergie im Fall der Höhle wie im Fall des hellen Saales die gleiche
war.
Sie sitzen an einem Ort völliger Stille. Das kleinste Geräusch, etwa das Herunterfallen
eines Wassertropfens, hat eine grosse Wirkung. - Sie sitzen in einem Sinfoniekonzert. Ob
eine Geige mehr oder weniger spielt, hat keine nennenswerte Wirkung, obwohl die
Schallenergie einer Geige viel höher ist, als diejenige eines fallenden Wassertropfens.
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
12
Weitere Fragen:
-Ist ein Preisaufschlag von 1 Fr. viel oder wenig?
-Ist der Zuwachs von 50 g viel oder wenig?
-Wie genau können Sie Strecken im cm-Bereich und im Meter-Bereich schätzen?
-Sie geben a) reinem Wasser, b) einem stark gesüssten Getränk einen Teelöffel Zucker
zu...
Wir merken: Es kommt auf den relativen Zuwachs an und nicht auf die absolute
physikalische Grösse. Je mehr schon vorhanden ist, desto weniger wird ein Zuwachs
wahrgenommen.
Bereich
Physikalische Grösse
Empfindungsgrösse
Hören
Schalldruck (Pa)
Schallintensität (W / m2 )
Lichtintensität (W / m2 )
Tastdruck, Gewichtskraft
Konzentration in %
Frequenz f
Lautstärkepegel
Lautstärkepegel
"Helligkeit"
Schwere-Empfindung
Geschmacksempfindung
Tonabstand (Intervall)
Sehen
Tasten
Schmecken
Musik
Schmerz- und Temperaturempfinden fallen aus dem Rahmen. In diesen Bereichen lassen
sich auch keine Versuche anstellen, ohne dass die Person Schaden erleidet.
Die subjektiv empfundene Lautstärke eines Tones (Referenzton 1000 Hz) verläuft nicht
linear zur physikalisch einwirkenden Druckschwankung aufs Trommelfell, sondern
logarithmisch zu dieser. Etwas plakativ kann das sogenannte Weber-Fechnersche Gesetz
so ausgesprochen werden:
Unsere körperliche Wahrnehmung logarithmiert die physikalische Einwirkung.
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
13
Dezibel-Skala
Physikalische Grösse:
Massgeblich für das Ohr ist der Schalldruck in Pa (Pascal) = N / m2 .
Hörschwelle: 0.00002 Pa
(Zum Vergleich: Luftdruck Atmosphäre ca. 100'000 Pa; wir nehmen also bereits eine Druckschwankung wahr,
die den 5 Milliardsten Teil des Atmosphärendrucks ausmacht; so empfindlich ist unser Trommelfell.)
Schmerzgrenze: ca. 35 ... 60 Pa.
Zwischen Hörschwelle und Schmerzgrenze besteht somit ein Schalldruckverhältnis von
1 : 1 Million bis 1 : 3 Millionen: eine ausserordentliche Leistung unserer Ohren!
Schalldruckpegel: Logarithmische Dezibel-Skala für einen Ton von 1000 Hz.
0 dB = Hörschwelle, 130 dB = Schmerzgrenze.
Sei
L der Geräuschpegel in dB,
p der physikalisch wirkende Schalldruckunterschied in Pa,
p0 = 2 •10-5 Pa = Hörschwelle.
Es gilt:
p
p
L = 20 ‰ lgI ÅÅÅÅÅÅ
M
=
20
‰
lgH
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ L
p
0.00002 Pa
0
20 dB mehr bedeuten eine Verzehnfachung des Schalldrucks.
Schalldruckpegel L in dB: L = 20 • lg(p / 0.00002 Pa)
dB
0
10
20
30
40
50
60
70
80
90
100
110
120
------------------------------------------------------------------------------------------------------------------------------------------0.00002
0.0002
0.002
0.02
0.2
2
20
Schalldruck p in Pa = N / m2 (Hörschwelle: 0.00002 Pa)
Beispiele zur Dezibel-Skala
0
Hörschwelle
10
Atmen
20
Blätterrascheln
60
Unterhaltung zweier Personen
70
100
130
160
lebhafter Verkehr
Disco
Schmerzgrenze
Entfaltung Airbag, Pistole
(Quelle: www.wissen.de und www.sengpielaudio.com/TabelleDerSchallpegel.htm)
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
14
Die folgende Grafik zeigt den Verlauf der Dezibel-Skala (y-Achse) bei gleichmässig
zunehmendem Schalldruck (x-Achse). Im leisen Bereich werden kleinste Druckzunahmen
als starke Lautstärkezunahme empfunden. Im lauten Bereich flacht diese Sensibilität ab.
Der Verlauf entspricht einer Logarithmusfunktion. Allerdings entspricht die dB-Skala nicht
durchwegs der subjektiven Lautstärke-Empfindung.
x = Schalldruck in Pascal (= N / m2 );
y = Lautstärke-Pegel in dB.
20 Dezibel mehr bedeuten eine Verzehnfachung des Schalldrucks.
Es gilt: y
x
= 20•lg( ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ ) = 20•lg(50'000x)
0.00002
Quelle: Suva: Beat W. Hohmann: Musik und Hörschäden, Best.-Nr. 84001.d unter www.suva.ch
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
15
Quelle: Suva: Beat W. Hohmann: Musik und Hörschäden, Best.-Nr. 84001.d unter www.suva.ch
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
16
p
L = 20 dB ‰ lgH ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ L sei
0.00002 Pa
Aufgabe
In
L = Schallpegel in dB,
p = Schalldruck in Pa,
p0 = 0.00002 Pa = 2 •10-5 Pa = Hörschwelle des menschlichen Ohres bei 1000 Hz.
a) Wie gross ist die Lautstärke L für die Hörschwelle?
b) Um wie viele dB nimmt die Lautstärke zu, wenn der Schalldruck verdoppelt wird?
c) Berechnen Sie den Schalldruck für 40 dB (Gespräch), 100 dB (Motorrad ohne
Schalldämpfer), 120 dB (Flugzeugmotor in 4 m Abstand).
d) Wie lautet die Gleichung der Umkehrfunktion p = f(L)? Mittels dieser Umkehrfunktion
kann Teilaufgabe c) direkt gelöst werden.
Lösungen:
0.00002 Pa
a) L = 20 dB• lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) = 20 dB• lg(1) = 20 dB• 0 = 0 dB
0.00002 Pa
2p
p
2p
p
b) 20• lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) - 20• lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) = 20• [lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) - lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ )]
0.00002 Pa
0.00002 Pa
0.00002 Pa
0.00002 Pa
2p
p
= 20• lg[( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) : ( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) ] = 20• lg(2) ≈ 6 dB
0.00002 Pa
0.00002 Pa
p
p
p
c) 40 dB = 20 dB • lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) ï 2 = lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) ï 102 = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ
0.00002 Pa
0.00002 Pa
0.00002 Pa
ï 0.002 Pa = p.
Analog: 100 dB: 2 Pa; 120 dB: 20 Pa
L
L
p
p
L
d) ÅÅÅÅ
ÅÅÅ = lg( ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ) ï 10 ÅÅÅÅ20ÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ ï 0.00002 Pa •10 ÄÄÄÄ20ÄÄ = p(L)
20
0.00002 Pa
0.00002 Pa
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
17
11.9. Logarithmen, abgegriffene Buchseiten und frisierte Bilanzen
1881 bemerkte der amerikanische Astronom Simon Newcomb, dass in zahlreichen Logarithmentafeln die
ersten Seiten deutlich stärker abgegriffen waren als die hinteren. Das erschien ihm seltsam. Auf den ersten
Seiten musste man stets nachschlagen, wenn man mit Zahlen rechnete, deren erste von Null verschiedene
Ziffer eine 1 war (z.B. 1 47.28; 0.0 1 45; 0. 1 8). Dass die ersten Seiten abgegriffener waren, konnte nur
bedeuten, dass Zahlen, die mit einer 1 begannen, häufiger vorkamen als etwa Zahlen, die mit einer 9
begannen. Konnte das tatsächlich sein?
Newcombs Beobachtung geriet wieder in Vergessenheit, bis 1938 ein amerikanischer Elektroingenieur, Frank
Benford, das Phänomen erneut entdeckte. Er analysierte etwa 20'000 Zahlen, die auf verschiedenste Weise
zusammengekommen waren: Einwohnerzahlen amerikanischer Städte, physikalische Konstanten in
Formelsammlungen, Zeitungsauflagen, Entwässerungsgebiete von Flüssen, Zahlen aus der Zeitschrift
"Reader's Digest", usw. Tatsächlich: Rund 30% dieser Zahlen hatten eine 1 als führende Ziffer, ca. 17% eine
2 und ca. 12% eine 3. Das waren bereits 60% der untersuchten Zahlen!
Das Phänomen wurde genauer untersucht.
Nicht alle Zahlenlisten folgen diesem Benfordschen Gesetz, aber doch sehr viele, z.B. auch Daten in Bilanzen
und Rechnungsabschlüssen.
Die einfachste Form des Benfordschen Gesetzes betrifft die erste Ziffer ≠ 0 einer Zahl:
Die Wahrscheinlichkeit, dass diese erste Ziffer den Wert d hat (d e {1, ... , 9}), beträgt
d+1
p("erste Ziffer ist d") = lg( ÅÅÅÅÅÅÅÅ
ÅÅÅÅ )
d
Setzt man für d der Reihe nach die Ziffern 1 bis 9 ein, findet man folgende Wahrscheinlichkeiten, dass die
Ziffer d die führende Ziffer einer Zahl ist:
Ziffer 1 führend: 30.1%
Ziffer 4 führend: 9.7%
Ziffer 7 führend: 5.8%
Ziffer 2 führend: 17.6%
Ziffer 5 führend: 7.9%
Ziffer 8 führend: 5.1%
Ziffer 3 führend: 12.5%
Ziffer 6 führend: 6.7%
Ziffer 9 führend: 4.6%
4
Rechenbeispiel für d = 3: p("3 ist führende Ziffer") = lg( ÅÅÅÅ
) ≈ 0.125 ≈ 12.5%.
3
Benfords Gesetz der ersten Ziffer wurde erweitert. Man hat heute Formeln für die Wahrscheinlichkeiten der
2., 3., 4., ... Ziffer, ja sogar für Gruppen von Ziffern. Man kann also auch die Wahrscheinlichkeit angeben, mit
der etwa in einer Zahl die Gruppe 1 3 4 an 2. Stelle vorkommt, also etwa in 7 1 3 4 5. 8 3 2.
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
18
Damit ist es nun möglich, z.B. Bilanzen zu prüfen. So wiesen etwa die Zahlen des griechischen
Staatshaushaltes der jüngeren Gegenwart wesentliche Abweichungen vom Benfordschen Gesetz auf, was
auf Manipulationen hindeutet. Auch die belgische Bilanz fällt diesbezüglich schlecht aus.
Benfords Gesetz wird heute zur Überprüfung von Zahlenmanipulationen eingesetzt.
Das Manipulieren von Bilanzen wird damit sehr schwierig. Das Gesetz der ersten Ziffer (siehe Kasten oben)
kann man ja noch leicht berücksichtigen. Doch eine Bilanz so zu fälschen, dass auch alle Gesetze für die 2.,
3., ... Ziffer und für Gruppen von Ziffern gleichzeitig erfüllt sind, ist ein fast unmögliches Unterfangen, obwohl
die Kontroll-Formeln offen vorliegen.
Die Mathematiker haben in den letzten 30 Jahren recht konkret eingrenzen können, welche Arten von
Zahlensammlungen benford-verträglich sind und welche nicht. Es müssen Sammlungen sein, die sehr grosse
und sehr kleine Werte umfassen und deren Zahlen durch möglichst viele, voneinander unabhängige Einflüsse
entstanden sind. Dass Bilanzen zu den benford-verträglichen Zahlen-Sammlungen gehören, ist Pech für
Erzeuger "kreativer" Abschlüsse.
So stand also eine skurrile Beobachtung an verschmutzten Logarithmentafeln am Anfang einer Entwicklung,
die schliesslich zu logarithmischen Gesetzen führte, mit deren Hilfe man Hinweise auf Bilanzmanipulationen
erhalten kann.
Die Nachfolger der alten Logarithmentafeln sind Computertastaturen:
In obiger Fotografie einer Computertastatur wird der Staub, der sich auf den Tasten "eingebrannt" hat, mittels
Bildbearbeitung stark übertrieben dargestellt (massive Kontrasterhöhung). Man erkennt deutlich, dass die
Tasten 1 und 2 am wenigsten "eingebrannten" Staub enthalten; offenbar werden diese Tasten viel öfter
benutzt als die übrigen Zifferntasten und dadurch dauernd gereinigt: das moderne Analogon zu Newcombs
Beobachtung an Logarithmentafeln. Oder wie Prof. Thomas Jech es ausdrückte: "When the '1' key on my old
computer gave out I was not surprised."
Infos z.T. aus: www.educ.ethz.ch/unt/um/mathe/ana/benford
Schlusszitat aus: www. math.psu.edu/jech/preprints/digits.pdf
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
19
11.10. Die Logarithmische Spirale
Vom Zentrum aus verlaufen 12 Speichen nach aussen. Eine Drehung um 30° im Gegenuhrzeigersinn führt
von einer Speiche zur nächsten und repräsentiert einen Halbtonschritt in der gleichstufig-temperierten
Tonleiter (c - cis - d - dis ...). Nach 12 Drehschritten um je 30° ist eine Umdrehung vollendet.
Die Länge der Speichenstrecke vom Zentrum zu einem der markierten Töne repräsentiert die Frequenz des
Tones (als Vielfaches von f = 261.8 Hz = Frequenz des "Schlüssel-c").
Nach einer Umdrehung hat sich die Frequenz jeweils verdoppelt und man hat den um eine Oktave höheren
Ton erreicht.
Als Bild entsteht eine logarithmische Spirale.
Fortschreiten im Gegenuhrzeigersinn: aufsteigende chromatische Tonleiter.
Fortschreiten im Uhrzeigersinn: absteigende chromatische Tonleiter.
Annäherungen an die Logarithmische Spirale in der Natur: Ammonit, Föhrenzapfen, Sonnenhut
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
20
Der "gesunde Menschenverstand" sagt:
Wenn ich eine Figur auf dem Fotokopierer vergrössere (z.B. auf Transparentfolie),
dann kann das vergrösserte Bild mit dem ursprünglichen Bild nicht mehr zur
Deckung gebracht werden.
Die Logarithmische Spirale widerlegt den "gesunden Menschenverstand":
Die unvergrösserte Originalfigur wird durch eine einfache Drehung
deckungsgleich mit der vergrösserten Figur:
Diese Eigenschaft wird Selbstähnlichkeit genannt.
Etwas plakativ ausgedrückt:
Die Logarithmische Spirale "ist" ihre eigene Vergrösserung.
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
21
11.11. Der natürliche Logarithmus, die Eulerzahl e
Ausblick Fachhochschule, Passerelle, KME
Kernideen
1. Die Eulerzahl e entsteht in Prozessen mit fortlaufender Verzinsung, wie
sie in der Natur bevorzugt vorkommen (Bakterien warten nicht 1 Jahr ab, bevor
sie sich "verzinsen".)
Die Zahl e
ist eine der wichtigsten Zahlen der
höheren Mathematik.
2. Die Exponentialfunktion y = ex ist deshalb so zentral, weil sie ihre
eigene Ableitung ist. Das heisst: Der Funktionswert e x gibt für jede Stelle x
gerade die Steigung der Tangente an den Funktionsgraphen an. Die Funktion y =
ex steigt also gerade so stark weiter an, wie ihr aktueller Funktionswert
beträgt ("Wer hat, dem wird gegeben").
Herleitung der Eulerzahl e
Wir stellen uns eine sehr grosszügige Bank vor, die unser Kapital mit einem
Zinssatz von p = 100% verzinst (Aufzinsfaktor q = 2). Unser Startkapital
K0 sei 1. Normalerweise wird nach einem Jahr verzinst:
Jährliche Verzinsung:
nach 1 Jahr:
K1 = H1 + 1L1
nach x Jahren: Kx = H1 + 1Lx
Nun sei die Bank noch grosszügiger und verzinse bereits nach einem halben Jahr.
Dadurch fahren wir noch besser (warum?):
1Å L = AH1 + ÅÅÅ
1Å L E
K ÅÅÅ12 =H1 + ÅÅÅ
2
2
Halbjährliche Verzinsung:
1Å Jahr:
nach ÅÅÅ
2
K1
1Å L
= H1 + ÅÅÅ
2
1Å L
nach 1.5 Jahren: K1.5 = H1 + ÅÅÅ
2
nach 1 Jahr:
2 0.5
1
2
3
nach x Jahren:
Kx
1Å L
= H1 + ÅÅÅ
2
2x
=
=
=
1Å L E
AH1 + ÅÅÅ
2
2 1
1Å L E
AH1 + ÅÅÅ
2
2 1.5
1Å L E
AH1 + ÅÅÅ
2
2 x
Nun können wir die Zinsperioden weiter verkürzen:
1
1
1
Verzinsung nach ÅÅÅ
3 , ÅÅÅ
4 , ..., ÅÅÅ
n Jahr:
n-tel-jährliche Verzinsung:
1Å Jahr:
nach ÅÅÅ
n
1Å )
K ÅÅÅ1n = (1 + ÅÅÅ
n
nach 1 Jahr:
nach x Jahren:
K1
Kx
1Å L E
= AH1 + ÅÅÅ
n
n
1
ÅÅÅ
n
1Å L
1Å L E
= H1 + ÅÅÅ
= AH1 + ÅÅÅ
n
n
1Å Lnx = AH1 + ÅÅÅ
1Å Ln Ex
= H1 + ÅÅÅ
n
n
n
n 1
1Å L . Wächst nun n gegen
Es entsteht der Aufzinsfaktor H1 + ÅÅÅ
n
1Å immer kleiner, so nähert
unendlich, d.h. werden die Zinsperioden ÅÅÅ
n
n
1Å L
sich der Ausdruck H1 + ÅÅÅ
immer
mehr
dem
Wert 2.71828... an. Dies
n
ist die Eulerzahl e, die
unendlich
unperiodisch sich
Printed
by Mathematica forviele,
Students
entwickelnde Kommastellen hat, also eine irrationale Zahl ist.
Die Zahl e ist also der Aufzinsfaktor bei p = 100% und laufender
Verzinsung ohne Wartezeit.
n
math_ges_soz11_log_april2014.nb
22
1Å L . Wächst nun n gegen
Es entsteht der Aufzinsfaktor H1 + ÅÅÅ
n
1Å immer kleiner, so nähert
unendlich, d.h. werden die Zinsperioden ÅÅÅ
n
n
1Å L
sich der Ausdruck H1 + ÅÅÅ
immer
mehr
dem
Wert 2.71828... an. Dies
n
ist die Eulerzahl e, die unendlich viele, unperiodisch sich
entwickelnde Kommastellen hat, also eine irrationale Zahl ist.
Die Zahl e ist also der Aufzinsfaktor bei p = 100% und laufender
Verzinsung ohne Wartezeit.
n
Stellen wir obige Überlegungen grafisch dar. Zwischen den
Zinsperioden interpoliert die Bank linear ("Marchzins"). Das
ergibt stückweise lineare Funktionen. Im Grenzfall n ö ¶ entsteht
die Exponentialfunktion K(x) = ex oder y = ex . Die MarchzinsSekanten werden zu Tangenten an der Graphen.
Jährliche Verzinsung. Dazwischen linearer Marchzins
x-Achse: Anzahl Jahre, y-Achse: Kapitalstand
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
23
Halbjährliche Verzinsung. Dazwischen linearer Marchzins
x-Achse: Anzahl Jahre, y-Achse: Kapitalstand
Man erkennt aus den beiden Diagrammen sofort folgende Eigenschaft:
Die Steigung einer "Marchzins-Sekante" ist gleich dem y-Wert
ihres Anfangspunktes.
Die Funktion steigt also gerade so stark weiter an wie ihr
aktueller Funktionswert beträgt: "Wer hat, dem wird gegeben."
Für den Grenzfall y = ex heisst das: Die Ableitung der Funktion
y = ex (das heisst die Steigung der Tangente an den Graphen) ist
an jeder Stelle x gerade gleich dem Funktionswert ex , d.h.
y' = y = ex .
Printed by Mathematica for Students
math_ges_soz11_log_april2014.nb
24
Funktion y = e x . Die Steigung der Tangente ist an jeder Stelle x
gerade so gross wie der Funktionswert y.
Der natürliche Logarithmus (logarithmus naturalis) ln(x):
Dies ist der Logarithmus zur Basis e.
y = ln(x) ist die Umkehrfunktion zu y = ex .
Printed by Mathematica for Students