Evolution und Robotik Teilnehmer

Evolution und Robotik
Teilnehmer:
David Schwalb
Elmo Feiten
Johannes Dyck
Konrad Seifert
Elisa Pipping
Hans Dettmar
Benjamin Schneider
Herder-Oberschule
Herder-Oberschule
Heinrich-Hertz-Oberschule
Heinrich-Hertz-Oberschule
Herder-Oberschule
Herder-Oberschule
Herder-Oberschule
Gruppenleiter:
Manfred Hild
Humboldt-Universität
Die Evolutionsmechanismen der Natur (natürliche Auslese, Kreuzung und Mutation) lassen
sich auch in der Robotik verwenden und können mobile autonome Roboter mit interessanten Verhaltensweisen hervorbringen.
Die Kursteilnehmer beschäftigten sich mit der Funktionsweise von künstlicher Evolution und der Dynamik rekurrenter, neuronaler Netze – das heißt deren Attraktoren und
Bifurkationen. In einer Simulationsumgebung evolvierten sie Roboter mit verschiedenen
Verhaltensweisen (z.B. Hindernisvermeidung und Tropismen) und analysierten die Netze
einzelner Individuen.
Zum Schluss des Kurses übertrugen sie die Netze auf einen realen Roboter und verglichen
jeweils dessen Verhaltensweise mit ihren theoretischen Überlegungen.
1
Evolution und Robotik
1
Einführung
Ursprünglich wurden Roboter designt, um Arbeiten zu verrichten, die Menschen nicht
übernehmen können oder um menschliche Arbeitskräfte zu ersetzen. Sie sind meist hoch
spezialisiert und besitzen besondere Eigenschaften, wie sehr viel Kraft oder eine große Genauigkeit. Dafür sind sie jedoch sehr unflexibel und können nur zu dem ihnen zugedachten
Zweck eingesetzt werden.
Im Gegensatz dazu sind die im weiteren Verlauf betrachteten Roboter autonom, d.h. sie
sind selbstständig und besitzen eine eigene Energiequelle, Sensorik, Motorik und sind intelligent. Aufgrund technischer Einschränkungen verfügen solche Maschinen jedoch nur
über die weniger komplexen Aspekte der Intelligenz, sind aber dennoch innerhalb gewisser
Grenzen in der Lage, einzuschätzen, Probleme zu lösen, zu reagieren, zu planen und zu
urteilen. Höhere Formen der Intelligenz, wie der gesunde Menschenverstand“, Kreativität
”
und ästhetisches Empfinden bleiben ihnen jedoch bislang verschlossen.
Es gibt zwei grundlegende Ansätze, intelligentes Verhalten zu simulieren. Im reaktiven Modell besitzt der Roboter keine Orientierung und kennt seine Umgebung nicht. Er reagiert
spontan auf den aktuellen Input und betreibt keine langfristige Planung. Deliberativ aufgebaute Roboter besitzen ein Weltmodell, planen voraus, benötigen dafür aber viel Zeit
und sind im Vergleich zum reaktiven Modell träge. Beide Ansätze haben ihre Vor- und
Nachteile, somit ist ein Kompromiss zwischen beiden die beste Lösung. Da es sehr schwer
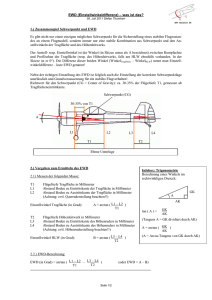
Abbildung 1.1: Hier sind sechs miteinander verbunden Servomotoren zu sehen, welche sich
allein durch die Motorenbewegungen fortbewegen sollen. Durch die künstliche Evolution
lernt dieses Gebilde bereits nach kurzer Zeit zu laufen“.
”
2
ist das Verhalten solcher intelligenten, autonomen Roboter explizit zu programmieren orientiert man sich an der Natur und macht sich das Prinzip der Evolution zu Nutzen. Es
gibt beispielsweise Aufgaben, die so komplex sind, dass es nahezu unmglich ist sie durch
gezielte berlegungen programmiertechnisch zu lösen (siehe Abbildung 1.1).
2
Künstliche Evolution
Um solche Roboter herzustellen, bedient man sich einer Simulation des natürlichen Evolutionsprozesses, basierend auf Selektion, Mutation und Rekombination. Hierbei steht das
Verhalten der Roboter für den Phänotypen in der Biologie und der Vektor, welcher das Verhalten definiert, findet seine Entsprechung in dem Genotypen. Konkret wird jedem Roboter
ein sogenannter Fitness-Wert“ zugeordnet, der seine Fähigkeit widerspiegelt, seine Auf”
gabe effefktiv zu erledigen. Anhand dieses Wertes wird bestimmt, welche Genotypen in die
nächste Generation übernommen werden - diejenigen mit den niedrigsten Fitness-Werten
fallen der Selektion zum Opfer.
Roboter in Testwelt
Abbildung
Genotyp
Ph notyp
Zielverhalten
Fitness
(Verhaltensanalyse, Fitness-Funktion)
Generationx
Gen1
Fit1
53
Gen2
Fit2
37
Genn
Fit3
67
Generationx+1
Mutation, X-Over,
Rekombination
Abbildung 2.2: Künstliche Evolution
Rekombination bedeutet, dass zwei Genotypen an derselben Stelle zertrennt und die hinteren Teile vertauscht werden. Durch Mutation werden schließlich einige der Genotypen
zufällig an einer Stelle verändert, bevor die neue Generation von Robotern erschaffen wird.
3
Crossover-Stelle
mutiertes Gen
ElternChromosom 1
Nachkomme 1
Nachkomme 2
ElternChromosom 2
Abbildung 2.3: Rekombination und Mutation
3
Neuronale Netze
Ein neuronales Netz (wie beispielsweise auch das menschliche Gehirn) besteht aus mehreren
Neuronen. Ein Neuron wiederum fungiert als signalverarbeitendes Element, das von außen
oder von anderen Neuronen Signale empfängt und sie verarbeitet bzw. weiterleitet.
weitere Synapsen
und Neuronen
Synapsen
Axon
Neuron
Abbildung 3.4: Schematische Darstellung eines Neurons
Die Funktionsweise ist wie folgt vorstellbar: Ein Neuron wird von einer oder mehreren
Synapsen (die wiederum von anderen Neuronen kommen) umlagert. Durch diese Synapsen können elektrische Impulse an das Neuron weitergeleitet werden, die erregend oder
hemmend wirken. Wird das Neuron ausreichend erregt, so feuert“ es, das heißt, es sen”
det seinerseits einen elektrischen Impuls, der durch sein Axon geht und sich dann auf die
Synapsen verteilt, die den Imupls wiederum an weitere Neuronen weiterleiten können.
x1
x2
xn
w1
A
w2
f
y
wn
Abbildung 3.5: Mathematisches Modell eines Neurons
4
Um sich das Prinzip eines neuronalen Netzes für die künstliche Evolution zu Nutze zu
machen, benutzt man ein sehr abstraktes Modell-Neuron. Das Bild zeigt dieses ModellNeuron, das n x-Werte als Input bekommt (x1 , x2 , . . . , xn ), xn ∈ (−1, +1). Jeder dieser
Werte verfügt über eine Gewichtung (w1 , w2 , . . . , wn ). Hierbei benötigt man lediglich Werte
in kleineren Bereichen, so also zum Beispiel wi ∈ [−10, 10]. Aus diesen Werten berechnet
sich die sogenannte Aktivität A des Neurons, nämlich durch:
A :=
n
X
(1)
xi wi
i=1
Die Ermittlung des Output-Wertes, der weitergegeben wird, findet durch eine geeignete
Funktion f statt, also: y := f (A).
tanh(A)
1.0
0.8
0.6
0.4
0.2
A
0.0
−4
−3
−2
−1
0
1
2
3
4
−0.2
−0.4
−0.6
−0.8
−1.0
Abbildung 3.6: Graph des Tangens Hyperbolicus
tanh(5*A)
1.5
1.0
0.5
A
0.0
−4
−3
−2
−1
0
1
2
3
4
−0.5
−1.0
−1.5
Abbildung 3.7: Graph des 5-fach in A-Achse gestauchten Tangens Hyperbolicus
Hierfür eignet sich besonders die oben abgebildete Funktion Tangens Hyperbolicus (tanh),
da sie sehr vielseitig einsetzbar ist. Durch Änderung der Gewichtungen w1 , w2 , . . . , wn kann
die Funktion stark verändert werden. Wählt man ein hohes w, wird die Funktion soweit
gestaucht, dass sie im Extremfall zu einer Sprungfunktion wird, die der Signum-Funktion
ähnelt. Wählt man das w dagegen sehr klein, so entsteht im Prinzip eine Null-Funktion.
Zusätzlich hat die tanh-Funktion in einer sehr kleinen x-Umgebung um 0 einen nahezu
linearen Verlauf.
5
tanh(0.5*A)
1.0
0.8
0.6
0.4
0.2
A
0.0
−4
−3
−2
−1
0
1
2
3
4
−0.2
−0.4
−0.6
−0.8
−1.0
Abbildung 3.8: Graph des 5-fach in A-Achse gestreckten Tangens Hyperbolicus
Somit erhält man ein Neuronenmodell, das wie folgt aussieht:
t∈N
xi (t) ∈ (−1; 1)
wij ∈ R
die Zeit
Signal des Neurons xi zum Zeitpunkt t
Verbindungsgewicht von Neuron j zu Neuron i
(2)
(3)
(4)
Es gibt Input-Neuronen (Sensorsignale), darunter optional ein Bias-Neuron (mit konstantem Wert 1) und Output-Neuronen (Motorsignale), sowie Hidden-Neuronen (alle anderen).
n
m
Anzahl aller Neuronen
m < n Anzahl der Input-Neuronen (inkl. Bias)
xi (t + 1) := tanh
à n
X
(5)
(6)
(7)
!
wij xj (t) ,
i = (m + 1) . . . n.
(8)
j=1
Zwar besteht das menschliche Gehirn, wie bereits erwähnt, aus mehreren hundert Millionen
Neuronen, jedoch kann man schon mit nur zwei Neuronen viel anfangen.
x1
x2
1 (Bias)
10
10
A tanh
y
10
Abbildung 3.9: Neuronale Realisierung der boolschen Oder“-Funktion
”
6
Wählt man (wie im obigen Bild) beispielsweise die Gewichtungen der zwei Input-Werte sehr
hoch, so wird die tanh-Funktion derart gestaucht, dass sie im Prinzip zu einer Sprungfunktion wird. Zusätzlich existiert in diesem speziellen Anwendungsfall noch ein sogenanntes
Bias-Neuron, das unabhängig von äußeren Werten stets den Wert 1 an das Neuron weiterliefert und über eine Gewichtung von 10 verfügt. Es ergibt sich:
A = 10 ∗ x1 + 10 ∗ x2 + 10
y = f (A) = tanh(10 ∗ x1 + 10 ∗ x2 + 10)
(9)
(10)
Stellt man sich nun vor, dass die Input-Werte nur -1 oder +1 annehmen können, ergeben
sich vier Möglichkeiten:
x1 x2
-1 -1
-1 +1
+1 -1
+1 +1
y
tanh(−10 − 10 + 10) = tanh(−10) = -1
tanh(−10 + 10 + 10) = tanh(10) = +1
tanh(10 − 10 + 10) = tanh(10) = +1
tanh(10 + 10 + 10) = tanh(30) = +1
Tabelle 1: Wertetabelle: logisches Oder“
”
x1
x2
1 (Bias)
10
A tanh
10
y
-10
Abbildung 3.10: Neuronale Realisierung der boolschen Und“-Funktion
”
Ebenso ist selbstverständlich auch eine Schaltung für das logische Und“ möglich. Dafür
”
wird lediglich die Gewichtung des Bias verändert und zwar zu -10. Es ergibt sich folgendes:
A = 10 ∗ x1 + 10 ∗ x2 − 10
y = f (A) = tanh(10 ∗ x1 + 10 ∗ x2 − 10)
(11)
(12)
Um diese einfachen logischen Schaltungen darzustellen, benötigt man also tatsächlich nur
ein Neuron. Die Darstellung des Xor (exklusives Oder) ist zwar ein wenig aufwändiger, ist
aber trotzdem möglich. Außerdem ist durch die Kombination zweier Neuronen noch der
Aufbau von Hochpassfiltern, Tiefpassfiltern, Verstärkern, An-/Ausschaltern und weiteren
Funktionen möglich.
Trotzdem stellt sich natürlich die Frage, welchen konkreten Vorteil neuronale Netze bieten. Ebenso wie die künstliche Evolution ist auch das Prinzip eines neuronalen Netzes
7
x1 x2
-1 -1
-1 +1
+1 -1
+1 +1
y
tanh(−10 − 10 − 10) = tanh(−30) = −1
tanh(−10 + 10 − 10) = tanh(−10) = −1
tanh(10 − 10 − 10) = tanh(−10) = −1
tanh(10 + 10 − 10) = tanh(10) = +1
Tabelle 2: Wertetabelle: logisches Und“
”
der Natur entnommen, da es offensichtlich funktioniert. Außerdem ist ein neuronales Netz
sehr einfach zu evolvieren, da nur wenige Parameter existieren, nämlich die Gewichtungen w1 , w2 , . . . , wn . Tatsächlich enthalten die Genotypen als Informationen lediglich die
Gewichtungen der einzelnen Verbindungen.
4
Die Fitnessfunktion
Wenn man eine bestimmte Anzahl von Individuen künstlich evolviert, so bedient man sich
einer sogenannten Fitnessfunktion, welche die Leistung der einzelnen Individuen bestimmt
und somit hilft, die besten bzw. leistungsfähigsten einer Generation zu selektieren und in
die nächste zu übertragen. Das Resultat einer künstlichen Evolution hängt sehr stark von
der Form dieser Fitnessfunktion ab, welche sich mit Hilfe der Abbildung 4.11 beschreiben
lässt. Die Kategorien lassen sich hierbei wie folgt gegeneinander abgrenzen:
Autonome, intelligente
Roboter
implizit
intern
extern
explizit
klassische Geraete
funktional
behavioristisch
Abbildung 4.11: Implementationsmöglichkeiten der Fitnessfunktion
• Intern: die Fitnesswerte werden direkt aus den neuronalen Signalen berechnet.
• Extern: die Fitnesswerte werden mit Hilfe der Beurteilung eines externen Beobachters
erstellt.
8
• Behavioristisch: allein das Resultat ist für den Fitnesswert ausschlaggebend (wenn
die Aufgabe also lautet, von Punkt A nach Punkt B zu gelangen, so ist die Art und
Weise der Fortbewegung nicht von Interesse; ausschlaggebend ist die benötigte Zeit).
• Funktional: die konkrete Funktionsweise wird bewertet; z.B. wird vorgeschrieben, mit
welchen Bewegungen der Roboter von A nach B gelangen soll.
• Implizit: Anzahl von Variablen, Konstanten und Randbedingungen ist gering (in
unserem Beispiel wäre nur die Tatsache, dass der Roboter geradeaus fährt von Bedeutung, der Abstand eines Sensors von der Wand z.B. nicht).
• Explizit: Anzahl von Variablen, Konstanten und Randbedingungen ist hoch.
Beispiel einer Fitnessfunktion
Eine Fitnessfunktion könnte man wie folgt realisieren: Die Länge des Zeitraums, in dem der
Roboter geradeaus fährt, minus die Länge des Zeitraums, in dem er Kurven fährt (wobei
die Länge der Kurve ebenfalls von Bedeutung ist), plus die Entfernung des Roboters von
der vor ihm liegenden Wand. Je länger der Roboter also geradeaus fährt, desto höher ist
der Fitnesswert des entsprechenden Individuums. Wenn wir den Abstand der Sensoren von
der Wand mit Hilfe von neuen Variablen, die wir I1 und I2 nennen, angeben, so könnte die
Fitnessfunktion auch folgendermaßen lauten:
O1 + O2 |O1 − O2 | I1 + I2 + 2
−
−
,
2
2
4
(13)
Output, der den linken Motor ansteuert,
Output, der den rechten Motor ansteuert.
(14)
(15)
f (x) =
wobei
O1 :=
O2 :=
Hierbei sind I1 , I2 ∈ [−1, +1], wobei −1 bedeutet, dass der Roboter einen großen Abstand
von der vor ihm liegenden Wand hat und +1, dass er die vor ihm liegende Wand berührt.
Diese Fitnessfunktion ist ein gutes Beispiel für eine explizite, interne und funktionale Funktion.
5
Praktisches Beispiel
Als praktische Aufgabe wollten wir einen Roboter evolvieren, welcher sich mit drei IRAbstands-Sensoren in einer realen Welt zurecht findet. Mittels zweier Motoren, die von
zwei Output-Neuronen angesteuert werden, kann er sich frei in seiner Welt bewegen und
Hindernissen ausweichen. Das Experiment umfasste die folgenden Teilschritte:
1. In einem Seminarraum wurde die Welt aus drei Tischen und einem Teil der Wand
aufgebaut.
2. Die virtuelle Welt wurde als Weltpolygonzug per x-y-Koordinaten in den PC eingegeben. Hierzu wurde der World-Simulator benutzt.
9
Abbildung 5.12: Aufgebaute (links) und simulierte Welt (rechts).
3. Im Robot-Simulator wurden die Maße des Roboters als x-y-Koordinaten eingegeben,
wobei der Ursprung dem Drehpunkt entsprach.
4. Durch die Verknüpfung der Programme: World-Simulator, Robot-Simulator und Populations-Manager konnte die künstliche Evolution mit dem virtuellen Roboter in
der virtuellen Welt durchgeführt werden.
5. Das evolvierte neuronale Netz wurde auf den realen Roboter übertragen.
6. Der Roboter wurde nun in die Testumgebung gesetzt und gestartet.
Das Resultat des Experiments: Der Roboter hat in der realen Welt exploratives Verhalten
gezeigt, das heißt er fuhr in der Welt einen großen Bereich ab. Dabei stieß er nicht an
Hindernisse und fand erfolgreich den Weg aus spitzen Ecken und Sackgassen.
Wie sich zeigte, konnte der Roboter Tischbeinen nicht ausweichen, da derart dünne Gegenstände nicht in der Testwelt vorhanden waren, in welcher er evolviert wurde.
Linkes
SensorNeuron
0,7
-2,6
-1,6
-1,7
Rechtes
SensorNeuron
2,7
0,5
0
0
-0,5
Rechtes
MotorNeuron
-3,9
Rechtes
SensorNeuron
Linkes
MotorNeuron
-0,5
Mittleres
SensorNeuron
0
Rechtes
MotorNeuron
-3,9
0
0
-1,7
Mittleres
SensorNeuron
0
0
Linkes
MotorNeuron
0
-1,0
-1,0
Linkes
SensorNeuron
4,0
0,7
Linkes
MotorNeuron
-1,6
Mittleres
SensorNeuron
Linkes
SensorNeuron
0,5
0
0
Rechtes
MotorNeuron
0
Rechtes
SensorNeuron
0
0
Abbildung 5.13: Modifizierte Kopien des aus der Evolution entnommenen Netzes
10
Um die Auswirkungen eines veränderten Genotyps auf das Verhalten des Roboters zu
untersuchen, werden zum Schluss verschiedene neuronale Netze auf dem Roboter ausprobiert, die durch gezielte Modifikation aus dem ursprünglichen Netz abgeleitet wurden. In
Abbildung 5.13 sind drei dieser Netze zu sehen.
Verhalten des Roboters mit dem ganz links abgebildeten Netz: Das Verhalten des Roboters
veräanderte sich dahingehend, dass er bei frontalem Wandkontakt nach links anstatt nach
rechts auswich. Er konnte sich aus einer spitzwinkligen Ecke nicht mehr befreien.
Verhalten des Roboters mit dem in der Mitte abgebildeten Netz: Der Roboter rotierte um
sein rechtes Rad gegen den Uhrzeigersinn. Sobald der rechte Sensor dabei ein Hinderniss
erfasste, wechselte der Roboter die Drehrichtung.
Verhalten des Roboters mit dem ganz rechts abgebildeten Netz: War kein Hindernis in Sicht,
fuhr der Roboter geradeaus. War ein Gegenstand weniger als 10cm von ihm entfernt, dann
blieb er stehen. Bei weiterer Annäherung wich er entsprechend zurück - entfernte sich das
Objekt, so verfolgte er es.
Insgesamt konnte gezeigt werden, dass die künstliche Evolution neuronaler Netze geeignet
ist, einen mobilen Roboter mit einer gewünschten Verhaltensweise auszustatten – sowohl
in der Simulation, wie auch in der realen Welt.
Abbildung 5.14: Die Kursteilnehmer mit ihrem Roboter
11
Potenzsummen von ganzen Zahlen und Polynomen
Teilnehmer:
André Stenzel
Christian Rekittke
Jana Schulz
Jannis Hessel
Konrad Steiner
Pascal Gussmann
Robert Altmann
Heinrich-Hertz-Oberschule
Andreas-Oberschule
Andreas-Oberschule
Herder-Oberschule
Heinrich-Hertz-Oberschule
Heinrich-Hertz-Oberschule
Heinrich-Hertz-Oberschule
Gruppenleiter:
Olaf Teschke
Humboldt-Universität zu Berlin
Die Gruppe beschäftigte sich mit klassischen zahlentheoretischen Problemen
über den ganzen Zahlen und ihrer Variante über Polynomringen. Als Motivation wurde zunächst die scheinbar einfache Gleichung a+b = c betrachtet. Es
stellte sich heraus, dass sich im Falle von komplexen Polynomen eine starke
Aussage über die Anzahl der verschiedenen vorhandenen Nullstellen machen
lässt (Satz von Mason), die weitgehende Folgerungen impliziert. So kann zum
Beispiel elementar und elegant der Satz von Fermat für Polynome bewiesen
werden.
Auf der Suche nach vergleichbaren Resultaten in Z stöÿt man auf die abc Vermutung, aus der man ebenfalls die Unlösbarkeit einer Reihe von bekannten Gleichungen folgern könnte.
Danach wurde das Problem der Darstellbarkeit von Zahlen und Polynomen
als Summen von Potenzen untersucht. Mit klassischen Methoden wurden
der zwei-Quadrate-Satz und der vier-Quadrate-Satz von Lagrange bewiesen
und das analoge Problem für höhere Potenzen (Waring-Problem) diskutiert.
Für Polynome stellt sich heraus, dass dieses Problem eine anschauliche geometrische Interpretation besitzt und auf eine Frage über Sekantenvarietäten
zurückgeführt werden kann. Eine Dimensionsbestimmung liefert dann ein
umfassendes Resultat.
33
1
a +b =c
Im ersten Teil beschäftigen wir uns mit Gleichungen der Form a + b = c und
stellen fest, dass damit starke Einschränkungen für die Zahl der verschiedenen
Primfaktoren von a · b · c verbunden sind. Für Polynome werden wir eine
erstaunliche Abschätzung überraschend elementar beweisen und daraus z.B.
den Satz von Fermat für Polynome folgern.
1.1 Der Satz von Mason und Satz von Fermat für Polynome
1.1.1
Grundlegende Begrie
Es sei f ∈ C[x ], d.h. f ist ein Polynom mit komplexen Koezienten. Nach
dem Fundamentalsatz der Algebra zerfällt es in ein Produkt von Linearfaktoren
m
Y
f (x) = c · (x − αi ).
i=1
Dies lässt sich auch schreiben als
f (x) = c ·
r
Y
(x − αi )mi ,
i=1
dabei ist mi die Vielfachheit der Nullstelle βi . Der Grad des Polynoms deg(f )
ergibt sich dann als
r
X
deg(f ) =
mi .
i=1
Wir schreiben weiterhin n0 (f ) für die Anzahl der verschiedenen Nullstellen
n0 (f ) := r.
Damit gilt natürlich n0 (f ) ≤ deg(f ). Andererseits können beide Zahlen natürlich erheblich dierieren, z.B. hat (x − 1)1001 einen hohen Grad, aber
n0 = 1. Ziel ist es, unter bestimmten Voraussetzungen auch eine Abschätzung
in die andere Richtung zu erhalten.
34
1.1.2
Hilfsätze
Der ggt (gröÿter gemeinsamer Teiler) von Polynomen ist das Produkt aller gemeinsamen Primfaktoren, in unserem Fall (da ja komplexe Polynome
immer eine Nullstelle haben) der gemeinsamen Linearfaktoren.
Lemma 1.1. Sei f aus C[x ], dann gilt deg[ggt(f, f 0 )] = deg(f ) − n0 (f ).
Beweis: Sei αi eine Nullstelle von f mit Vielfachheit mi . Dann ist
f = (x − αi )mi · g,
x − αi - g
f 0 = mi · (x − αi )mi −1 · g + (x − αi ) · g 0
f 0 = (x − αi )mi −1 · [mi · g + (x − αi ) · g 0 ]
Oensichtlich gilt also:
(x − αi )mi −1 - mi · g + (x − αi ) · g 0
Jeder Linearfaktor (x − αi ) kommt also in der Linearfaktorzerlegung von f 0
genau mi − 1 mal vor.
⇒ deg[ggt(f, f 0 )] = (m1 − 1) + (m2 − 1) + ... + (mr − 1)
0
⇒ deg[ggt(f, f )] =
r
X
(mi − 1) = −r +
i=1
r
X
mi = deg(f ) − n0 (f )
i=1
Lemma 1.2. Seien f, g aus C[x ], dann gilt:
n0 (f · g) ≤ n0 (f ) + n0 (g)
Die Gleichheit gilt genau dann, wenn der ggt von f und g gleich 1 ist.
1.1.3
Satz von Mason - Beweis nach der Variante von Noah Snyder(2000)
Satz 1.3 (Mason 1983).
max{deg(f ), deg(g), deg(h)} ≤ no (f · g · h) − 1
35
Beweis (nach der Variante von Noah Snyder, 2000): Wir benutzen die
einfache Identität
f · g0 − f 0 · g = f · g0 + f · f 0 − f · f 0 − f 0 · g
= f (g 0 + f 0 ) − f 0 (f + g) = f · h0 − f 0 · h.
Es sind f · g 0 6= 0 und f 0 · g 6= 0, da f und g nicht konstant sind. Auÿerdem
gilt f · g 0 − f 0 · g 6= 0, da sonst f das Produkt f 0 · g teilen würde. Da f und g
teilerfremd sind, müÿte f | f 0 gelten, was schon wegen des kleineren Grades
unmöglich ist.
Nun gilt:
ggt(f, f 0 ) | f · g 0 − f 0 · g
ggt(g, g 0 ) | f · g 0 − f 0 · g
ggt(h, h0 ) | f · g 0 − f 0 · g
Da f, g, h paarweise teilerfremd sind, gilt:
ggt(f, f 0 ) · ggt(g, g 0 ) · ggt(h, h0 ) | f · g 0 − f 0 · g
⇒ deg[ggt(f, f 0 ) · ggt(g, g 0 ) · ggt(h, h0 )] ≤ deg(f · g 0 − f 0 · g)
Wir erhalten die Ungleichung
⇒ deg[ggt(f, f 0 ] · ggt(g, g 0 ) · ggt(h, h0 )] ≤ deg(f · g 0 ) = deg(f ) + deg(g) − 1
⇒ deg[ggt(f, f 0 )] + deg[ggt(g, g 0 )] + deg[ggt(h, h0 )] ≤ deg(f ) + deg(g) − 1
Lemma 1.1
⇒
deg(f )−n0 (f )+deg(g)−n0 (g)+deg(h)−n0 (h) ≤ deg(f )+deg(g)−1
⇒ deg(h) ≤ n0 (f ) + n0 (g) + n0 (h) − 1
Da f, g und h immer noch teilerfremd sind, gilt:
Lemma 1.2
⇒
deg(h) ≤ n0 (f · g · h) − 1
Da nun gilt f + g = h ⇔ f + (−h) = −g ⇔ g + (−h) = f , lässt sich analog
zeigen:
deg(f ) ≤ n0 (f · g · h) − 1
deg(g) ≤ n0 (f · g · h) − 1
Da die Ungleichungen für deg(f ), deg(g) und deg(h) gelten, gilt schlieÿlich
auch:
max{deg(f ), deg(g), deg(h)} ≤ n0 (f · g · h) − 1
36
1.1.4
Die FERMATsche Gleichung für Polynome
Es seien f, g, h paarweise teilerfremde, nicht konstante Polynome in C[x ].
Auf die Gleichung
f n + g n = hn
ist der Satz von Mason also anwendbar mit
deg(f n ) ≤ n0 (f · g · h) − 1
deg(g n ) ≤ n0 (f · g · h) − 1
deg(hn ) ≤ n0 (f · g · h) − 1
da, wenn die Ungleichung für den maximalen Grad gilt, sie natürlich auch
für alle Grade einzeln gilt.
Desweiteren lassen sich auch die rechten Seiten mit Lemma 2 als n0 (f ) +
n0 (g) + n0 (h) − 1 darstellen. Durch Summation erhalten wir
deg(f n ) + deg(g n ) + deg(hn ) ≤ 3(n0 (f ) + n0 (g) + n0 (h) − 1)
⇒ n · (deg(f ) + deg(g) + deg(h)) ≤ 3(deg(f ) + deg(g) + deg(h) − 1)
Somit kann die FERMATsche Gleichung für Polynome für n ≥ 3 keine Lösungen besitzen.
Für n = 2 gibt es übrigens die klassische Lösung (x2 − 1)2 + (2x)2 = (x2 +1)2 .
Man erhält sie zum Beispiel, indem man die rationalen Punkte auf dem Einheitskreis durch Geraden mit rationalem Anstieg durch (0, 1) parametrisiert
(dies liefert zudem auch alle Pythagoräischen Tripel, d.h. alle ganzen Zahlen
a, b, c mit a2 + b2 = c2 ).
1.2 Die abc-Vermutung
Wir versuchen, für ganze Zahlen mit a + b = c eine Art Mason-Satz zu
formulieren.
Es seien a, b, c ∈ Z paarweise teilerfremd.
Als Grad einer ganzen Zahl wird der Betrag der Zahl gewählt. Dies kann
z.B. durch die Division mit Rest motiviert werden - bei Polynomen hat der
Rest einen kleinerer Grad als der Divisor, bei ganze Zahlen einen kleineren
37
Betrag.
Wodurch könnte n0 ersetzt werden? Bei Polynomen wird die Anzahl der verschiedenen Nullstellen, also der Primfaktoren gezählt. Wir sind dort in der
einfachen Situation, dass alle Primfaktoren denselben Grad haben. Dagegen
treten im allgemeinen in der Primzerlegung
a=
n
Y
pimi
i=1
Faktoren mit unterschiedlichem Betrag auf. Wir denieren daher
N0 :=
n
Y
pi ,
i=1
also das Produkt der verschiedenen Primfaktoren.
1. Versuch:
Gilt max{|a|, |b|, |c|} ≤ N0 (a · b · c) für ganze Zahlen?
Gegenbeispiel:
210 + 1 = 1025 = 52 · 41
N0 (a · b · c) = 2 · 1 · 5 · 41 = 410 < 210 + 1
2.Versuch:
Ausgleich durch eine Konstante K ∈ R
max{|a|, |b|, |c|} ≤ K · N0 (a · b · c)
Gegenbeispiel:
n
a = 32 , b = −1
n
Es gilt ferner für alle n, dass 2n |(32 − 1) (induktiv leicht zu zeigen).
n
n
n
31 − 1
32 − 1
32 − 1
n
)
≤
N
(2
)
·
N
(
)
≤
2
·
⇒ N0 (3 − 1) = N0 (2 ·
0
0
2n
2n
2n
n
32
⇒ N0 (a · b · c) ≤ 1 · 3 · 2 · n
2
2n
3
−1
n
1
⇒ max{|a|, |b|, |c|} = 3
≤ k·3·2·
n
2
2n
n
38
⇒ Es existiert kein k ∈ R, sodass dies für alle n gilt!
Die Ungleichung würde aber stimmen, wenn die rechte Seite in eine minimal höhere Potenz als 1 erhoben würde. Dies führt zu folgender
Vermutung (abc-Vermutung). Seien a, b, c ∈ Z, a + b = c.
∀ ² > 0 ∃ K(ε) :
max{|a|, |b|, |c|} ≤ K(ε)N0 (a · b · c)1+²
Bisher sind keine Gegenbeispiele bekannt, und es gibt eine Reihe von
Ergebnissen, die auf die Richtigkeit der Vermutung hindeuten.
1.3 Die Anwendungen der abc-Vermutung
1.3.1
Die FERMATsche Gleichung
Seien x, y, z ∈ Z mit xn + y n = z n , n ∈ N.
Aus der abc-Vermutung folgt:
max{|xn |, |y n |, |z n |}
⇒
|xn | · |y n | · |z n |
⇒
(|x · y · z|)n
⇒
(|x · y · z|)n
⇒ (|x · y · z|)n−3ε−3
≤
≤
≤
≤
≤
K(ε) · N0 (xn · y n · z n )1+ε
(K(ε) · N0 (x · y · z)1+ε )3
K(ε)3 · N0 (x · y · z)3+3ε
K(ε)3 · (|x · y · z|)3+3ε
K(ε)3
(1) Wenn x · y · z ≥ 2, so muss oensichtlich ein n0 existieren, sodass gilt:
∀n ≥ n0 : (|x · y · z|)n−3ε−3 > K(ε)3 .
Für genügend groÿe n gibt es also nur die trivialen Lösungen mit x · y ·
z = 0.
(2) Fixiert man n ≥ 4, kann die Gleichung nur endlich viele Lösungen
haben, da ab einer gewissen Gröÿe von |x · y · z| die Ungleichung nicht
mehr erfüllt wird.
39
1.3.2
Die CATALANsche Gleichung
∀x, y, n ∈ N∗ : x n − y m = 1 hat für m, n ≥ 2 und y 6= 0 keine Lösung auÿer
32 − 23 = 1.
Annahme: Die CATALANsche Gleichung ist erfüllt.
(1) m = n = 2 ist nicht möglich, da die Dierenz zweier Quadrate 6= 0
immer gröÿer als 1 ist.
(2) Sei m > 2 ∨ n > 2
Mit der abc-Vermutung folgt dann:
max{xn , y m } ≤ k(²) · N0 (xn · y m )1+ε
⇒ m · ln(y) < n · ln(x) ≤ (1 + ε) · ln(N0 (xn · y m )) + ln(K(ε))
⇒
n · ln(x) ≤ (1 + ε) · ln(N0 (x · y)) + ln(K(ε))
≤ (1 + ε) · ln(x · y) + ln(K(ε))
m · ln(y) ≤ (1 + ε) · ln(N0 (x · y)) + ln(K(ε))
≤ (1 + ε) · ln(x · y) + ln(K(ε))
⇒ m · n · (ln(x) + ln(y)) ≤ (1 + ε) · (m + n) · (ln(x) + ln(y)) + (m + n) · ln(K(ε))
m · n > m + n gilt nach Voraussetzung (da m = n = 2 nicht möglich ist).
Demnach ist diese Ungleichung nur für endlich viele x, y erfüllt.
Also kann auch die CATALANsche Gleichung höchstens von endlich vielen
x, y erfüllt werden.
1.3.3
Die Gleichung xl + y m = z n
Seien x, y, z ∈ Z mit xl + y m = z n , l, m, n ∈ N \ {0, 1, 2, 3}.
Aus der abc-Vermutung folgt:
max{|xl |, |y m |, |z n |} ≤ K(ε) · N0 (xl · y m · z n )1+ε
|xl | · |y m | · |z n | ≤ (K(ε) · N0 (x · y · z)1+ε )3
|x|l · |y|m · |z|n ≤ K(ε)3 · N0 (x · y · z)3+3ε
40
Fixiert man l, m, n ≥ 4, kann die Gleichung nur endlich viele Lösungen haben, da ab einer gewissen Gröÿe von |x · y · z| die Ungleichung sonst nicht
mehr erfüllt wird. Ebenso sieht man, dass für hinreichend groÿe l, m, n keine
Lösung mehr existieren kann.
2
Das Waring-Problem für ganze Zahlen
In diesem Abschnitt beschäftigen wir uns mit der Frage, ob man eine ganze
Zahl n als Summen von Potenzen
n = ak1 + . . . akg
darstellen kann und wieviele Summanden man dazu benötigt. Wir beginnen
mit dem Fall k = 2, also Summen von Quadraten.
2.1 Der Zwei-Quadrate-Satz
Welche Zahlen lassen sich als Summe zweier Quadrate schreiben? Wir probieren z.B.
2 = 1 2 + 12 ,
20 = 42 + 22 ,
65 = 72 + 42 = 82 + 12 .
Es fällt auf, dass die Zahlen, die sich als Summe zweier Quadrate schreiben
lassen, nur bestimmte Primfaktorzerlegungen haben. Der Grund dafür ist das
folgende Lemma:
Lemma 2.1. (A2 + B 2 ) · (U 2 + V 2 ) = (AU + BV )2 + (AV − BU )2
Diese Identität kann leicht durch Ausmultiplizieren berechnet werden.
Man kann sie aber auch interpretieren als die Betragsgleichung |z1 ||z2 | =
|z1 z2 | für komplexe Zahlen z1 = A + Bi, z2 = V + U i.
Korollar 2.2. Das Problem der Darstellung als zwei Quadrate kann auf
das Problem für Primfaktoren reduziert werden.
Welche Primzahlen sind als Summe zweier Quadrate darstellbar? Z.B.
sind
2 = 12 + 12 ; 53 = 22 + 72 ; aber 19 = 32 + 32 + 12
41
Wir beobachten, dass alle Rest 1 bei der Division durch 4 lassen. Tatsächlich
gilt:
Satz 2.3. Sei p eine ungerade Primzahl. p ist die Summe von zwei Quadraten genau dann, wenn gilt:
p ≡ 1(
mod 4)
Beweis: Wir beweisen zunächst die einfache Richtung. Wenn p die Summe von 2 Quadraten ist, dann muss eines der beiden Quadrate gerade und
eines ungerade sein. Selbiges gilt somit auch für die Zahlen selber. Da gilt:
a = 2n + 1 ⇔ a ≡ 1( mod 4) ∨ a ≡ 3( mod 4) ⇔ p2 ≡ 1(
b = 2k ⇔ bp ≡ 0( mod 4) ∨ b ≡ 2( mod 4) ⇔ p2 ≡ 0(
mod 4)
mod 4)
Somit gilt:
p ≡ a2 + b2 ( mod 4) ⇔ p ≡ 0 + 1(
mod 4) ⇔ p ≡ 1( mod 4)
Wenn p die Summe zweier Quadrate ist, ist es auch kongruent zu 1 mod 4.
Für den Beweis der Umkehrung benötigen wir folgendes Lemma:
Lemma 2.4. (i) (Satz von Wilson) p ist eine Primzahl genau dann, wenn
(p − 1)! ≡ −1(
(ii) Sei p eine Primzahl, dann ist ((
mod p)
p+1
p−1 2
)!) ≡ (−1) 2 (
2
mod p)
Beweis: (i) Jede Restklasse 6= 0 ist modulo einer Primzahl p invertierbar.
Im Produkt (p − 1)! erscheint damit also zu jeder Restklasse ihre Inverse.
Diese kürzen sich zu 1 mit Ausnahme von ±1, die ihre eigenen Inversen sind.
Daher ist das Produkt für Primzahlen −1.
Umgekehrt ist der ggt((p − 1)!, p) ≥ 2, wenn p keine Primzahl ist.
(ii) (p−1)! ≡ (−1)·1·. . .·(−
p−1 (i)
p−1 2
p−1 p−1
)(
) ≡ ((
)!) ·(−1) 2 ≡ −1(mod p).
2
2
2
Insbesondere gibt es für Primzahlen p ≡ 1( mod 4) eine Zahl x mit x2 +
1 = M p (dabei ist oenbar M ≤ p − 1), also haben wir ein Vielfaches
von p als Summe zweier Quadrate A2 + B 2 dargestellt. Wir beginnen nun
42
ein Reduktionsverfahren, um M zu verkleinern. Dabei setzen wir U ≡ A(
mod M ) und V ≡ B( mod M ). Es gilt dann U 2 + V 2 = M r mit r ≤ M − 1.
Wir verwenden nun erneut die Quadrateidentität 2.1 und erhalten
(A2 + B 2 ) · (U 2 + V 2 ) = (AU + BV )2 + (AV − BU )2 = M 2 rp.
Desweiteren ist oenbar AU +BV ≡ A2 +B 2 ≡ 0( mod M ) und AV −BU ≡
AB − BA ≡ 0( mod M ), daher teilt M die Zahlen AU + BV und AV − BU ,
und es gilt
(
AU + BV 2
AV − BU 2
) +(
) = rp, wir haben also ein kleineres Vielfaches
M
M
von p als Summe zweier Quadrate dargestellt. Der Schluÿ auf M = 1 folgt
durch Iteration.
Korollar 2.5. Jede Primzahl p ≡ 1( mod 4) läÿt sich eindeutig als Sum-
me zweier Quadrate darstellen.
Die Existenz einer Darstellung p = A2 + B 2 folgt aus dem eben bewiesenem Satz, die Eindeutigkeit aus der Zerlegung A2 + B 2 = (A + Bi)(A − Bi)
und der Tatsache, dass in Z + i Z die Primzerlegung eindeutig ist (letzteres
kann man z.B. aus der Existenz einer Division mit Rest bzgl. des Betrags
folgern).
Als Folgerung aus der Quadratidentität erhalten wir den zwei-QuadrateSatz für beliebige natürliche Zahlen:
Q
i
Korollar 2.6. n ∈ N mit der Primzerlegung n = ri=1 pm
ist als Summe
i
zweier Quadrate darstellbar genau dann, wenn jedes Pi ≡ 3( mod 4) nur mit
gerader Vielfachheit vorkommt.
2.2 Satz von Lagrange
Mit Hilfe der Ideen des vorigen Abschnitts beweisen wir nun analog den
Theorem 2.7 (Satz von Lagrange). Jede natürliche Zahl ist Summe von
vier Quadraten.
Beweis: Der Beweis verläuft analog zum zwei-Quadrate-Satz. Zunächst
wird eine Identität benutzt, die das Problem auf Primfaktoren zurückführt.
Dann nden wir durch Restklassenüberlegung eine Quadratzerlegung eines
43
Vielfachen. In einem Abstiegsverfahren, das wiederum die Identität benutzt,
können wir dann dieses Vielfache auf eins reduzieren.
Es gilt
(x21 + x22 + x23 + x24 )(y12 + y22 + y32 + y42 ) = z12 + z22 + z32 + z42
mit
z1 = x1 y1 + x2 y2 + x3 y3 + x4 y4
z2 = x1 y2 − x2 y1 + x3 y4 − x4 y3
z3 = x1 y3 − x3 y1 + x4 y2 − x2 y4
z4 = x1 y4 − x4 y1 + x2 y3 − x3 y2 .
Diese Identität kann man übrigens analog zur zwei-Quadrate-Identität als
Betragsgleichung von Produkten aunden, in disem Fall im Schiefkörper der
Quaternionen.
Ferner ist 2 = 12 + 12 + 02 + 02 . Es genügt also zu zeigen, daÿ jede Primzahl
Summe von 4 Quadraten ist.
Es sei also p eine ungerade Primzahl. Die p+1
Zahlen x2 mit 0 ≤ x ≤ p−1
2
2
2
sind paarweise inkongruent mod p, ebenso die p+1
Zahlen
−1
−
y
mit
2
0 ≤ y ≤ p−1
. Da es genau p Restklassen mod p gibt, dies aber insgesamt
2
p + 1 Zahlen sind, gibt es ein x, sodass x2 ≡ −1 − y 2 ( mod p) ist. Ein
Vielfaches von p lässt sich also in der Form 1 + x2 + y 2 darstellen:
m · p = 0 2 + 1 2 + x2 + y 2
¡ ¢2
Darin ist 0 < m < p (wegen 1 + x2 + y 2 < 1 + 2 p2 < p2 ). Es sei m0 p das
kleinste Vielfache von p, welches sich in der Form
m0 p = x21 + x22 + x23 + x24
mit 0 < m0 < p darstellen lässt, worin x1 , x2 , x3 , x4 nicht alle durch p und
auch nicht durch m0 teilbar sind. Angenommen, es sei m0 > 1. Aus der
Minimaleigenschaft von m0 folgt, dass dann m0 ungerade sein muss. Wäre
m0 gerade, so hätten wir
x1 + x2 + x3 + x4 ≡ x21 + x22 + x23 + x24 ≡ 0( mod 2)
d.h., die xi sind zu je zweien kongruent mod 2. Es sei o.B.d.A. x1 ≡ x2 (
mod 2) und x3 ≡ x4 ( mod 2). Dann haben wir die Darstellung
µ
¶2 µ
¶2 µ
¶2 µ
¶2
x1 + x2
x1 − x2
x3 + x4
x3 − x4
m0
·p=
+
+
+
2
2
2
2
2
44
im Widerspruch zur Minimalität von m0 . Man kann also
xi = bi · m0 + yi
mit (i = 1, 2, 3, 4) setzen, wobei bi so gewählt wurde, dass |yi | < 12 m0 ist. Da
x1 , x2 , x3 , x4 nicht alle durch m0 teilbar sind, ist wenigstens ein yi > 0. Somit
ist
µ
¶2
1
2
2
2
2
0 < y 1 + y2 + y3 + y4 < 4 ·
m0 = m20 .
2
Aus xi = bi m0 + yi folgt andererseits
y12 + y22 + y32 + y42 ≡ 0( mod m).
Daher ist
y12 + y22 + y32 + y42 = m1 · m0
mit 0 < m1 < m2 . Es folgt demnach die Darstellung
m20 m1 p = z12 + z22 + z32 + z42 .
Jedes der zi ist darin aber wegen xi ≡ yi (m0 ) durch m0 teilbar, also zi = m0 ti .
Es folgt
m1 p = t21 + t22 + t23 + t24
mit 0 < m1 < m0 < p, was ein Widerspruch zur Minimaleigenschaft von m0
ist. Es muss somit m0 = 1 sein, q.e.d.
2.3 Das Waring-Problem
In seinem Buch M editationes Algebraicae schrieb Waring 1770: Jede Zahl
ist Summe von neun Kubikzahlen, neunzehn Biquadraten und so weiter... Zuvor hatte Lagrange bereits bewiesen, dass jede Zahl als Summe von vier
Quadratzahlen darstellbar ist (siehe 2.7). Daher wurde nach Waring das folgende Problem benannt:
Problem 2.8 (Waring-Problem). Gibt es zu jedem Exponenten k eine
kleinste Zahl g(k), so dass jede natürliche Zahl n als Summe
n = ak1 + · · · + akg(k)
von k -ten Potenzen darstellbar ist?
45
Hilbert bewies 1909, dass ein solches g(k) für alle k ∈ N existiert. Die
Bestimmung der Zahlen g(k) erwies sich als deutlich schwieriger und wurde erst in den letzten Jahrzehnten abgeschlossen. Warings Vermutung, dass
g(3) = 9 und g(4) = 19 ist, konnten gezeigt werden. Allgemein gibt es drei
Fälle, wobei im Hauptfall das folgende Resultat gilt:
Theorem 2.9. Sei k > 4 und 2k · {( 32 )j } + [( 32 )j ] ≤ 2k . Dann ist
3
⇒ g(k) = 2k + [( )k ] − 2.
2
Der Beweis ist allerdings extrem schwierig.
Bei weiteren Untersuchungen stellt man fest, dass oft nur wenige Zahlen
wirklich g(k) Summanden benötigen. So sind im Fall k = 3 die Zahlen
23 = 2 · 23 + 7 · 13 und 239 = 53 + 3 · 33 + 4 · 23 + 13
die einzigen Zahlen, die neun Kuben benötigen. Weitere fünfzehn Zahlen
benötigen acht Kuben (die gröÿte ist 8042), alle anderen höchstens sieben.
Dies führt auf das bisher ungelöste
Problem 2.10 (Groÿes Waring-Problem). Finde die Zahl G(k), das ist
die kleinste Anzahl, so dass sich fast alle natürlichen Zahlen (d.h. bis auf
endlich viele) als Summe von G(k) k -ten Potenzen schreiben lassen.
Dieses Problem ist noch deutlich schwerer und weitgehend ungelöst. So ist
z.B. unklar, ob G(3) = 7. Bisher weiÿ man nur, dass G(2) = 4 und G(4) = 16.
3
Das Waring-Problem für Polynome
In diesem Abschnitt betrachten wir das analoge Problem für Polynome aus
C[x ], d.h. die Frage, wann man ein Polynom als Summe von Potenzen anderer
Polynome darstellen kann. Wir werden im ersten Teil schnell sehen, dass
diese Frage relativ leicht beantwortbar, aber nicht besonders interessant ist.
Deshalb werden wir uns auf das Problem der Darstellung als Potenzsummen
von linearen Polynomen einschränken. Es erweist sich, dass dies eine schöne
geometrische Interpretation und eine anschauliche Antwort besitzt.
46
3.1 Potenzsummen beliebiger Polynome
Wir beginnen wieder mit dem quadratischen Fall. Dieser ist besonders einfach
wegen der Identität
P2 = (
P +1 2
P −1 2
) + (i
),
2
2
d.h. jedes komplexe Polynom P (mit beliebig vielen Variablen!) ist Summe zweier Quadrate. Stimmt das auch für Kuben? Wir untersuchen dies im
einfachen Fall des Polynoms x.
Satz 3.1. x ist nicht Summe zweier Kuben.
Beweis: Allgemein lässt sich jede Summe zweier Kuben darstellen als:
A3 + B 3 = (A + B) · (A + ξB) · (A + ξ 2 B),
wobei ξ eine dritte Einheitswurzel 6= 1 ist. Damit müsste x als Polynom 1.
Grades darstellbar sein als Produkt dreier Faktoren. Von diesen Faktoren
muss demnach einer ersten Grades und zwei konstant sein. Da dafür oensichtlich A und B konstant sein müssten (leicht nachzurechnen), führt dies
automatisch zu einem Widerspruch, da dann A3 + B 3 6= x.
Übrigens könnten wir den Beweis auch mit dem Satz von Mason führen.
Die Anwendung auf x = A3 + B 3 liefert nämlich n0 (A) + n0 (B) + 1 − 1 ≥
max{deg(A3 ), deg(B 3 )}, also deg(A) + deg(B) ≥ 3 max{deg(A), deg(B)}.
Dies ist unmöglich für nichtkonstante A und B .
Damit kann nicht jedes Polynom als Summe zweier Kuben dargestellt werden. Wir können aber durch Untersuchung der Darstellung von x zeigen, dass
jedes Polynom Summe dreier Kuben ist; es gilt nämlich
³x
6
+1
´3
´3 µ −x ¶3
+
−1 + √
= x.
6
108
³x
Durch Substitution erhält man also für jedes beliebige komplexe Polynom P
(mit beliebig vielen Variablen!):
µ
P
+1
6
µ
¶3
+
¶3 µ
¶3
P
−P
−1 + √
.
6
108
47
Demnach ist jedes Polynom als Summe von drei Kuben darstellbar.
Analog kann man x auch als Summe von höheren Potenzen darstellen, man
sieht allerdings bereits hier, dass diese nicht sehr ergiebig, sondern im Gegenteil sogar sehr kompliziert sind. Als abstraktes Resultat mag eine solche
Darstellung befriedigen, aber das Resultat sieht sehr unschön und willkürlich aus. Eine solche Zerlegung sagt uns nicht über die Eigenschaften von P ,
zumal die einzelnen Summanden höheren Grad als P haben. Ezienter wäre
eine Darstellung als Potenzsumme von Polynomen mit kleinerem Grad, am
besten von linearen. Dies soll uns im folgenden beschäftigen. Dazu führen
wir zunächst den Begri eines homogenen Polynoms ein.
3.2 Homogenisierung
Denition 3.2. Ein Polynom P ∈ C[x0 , . . . , xn ] heisst homogen vom
Grad d, wenn P (λx0 , . . . , λxn ) = λd P (x0 , . . . , xn ) für beliebige λ ∈ C gilt.
Bemerkung: Diese
ist äquivalent zu der Tatsache, dass in der
P Eigenschaft
i0
i1
Darstellung P = i0 ,...,in x0 ·x1 ·...·xinn für alle Monome gilt: i0 +· · ·+in = d.
Homogene Polynome haben den Vorteil, dass sich bei Summation der Grad
nicht verändern kann (es sei denn, es ergibt sich das Nullpolynom). Wir können durch eine leichte Modikation jedes Polynom aus C[x1 , . . . , xn ] in eine
homogene Form überführen, indem wir einfach in jedem Monom den Grad
durch Multiplikation mit Potenzen einer zusätzlichen Variablen x0 auüllen.
So wird zum Beispiel aus 3x21 +4x1 +1 das Polynom 3x21 +4x1 x0 +x20 . Oenbar
ist diese Zuordnung umkehrbar eindeutig.
Im Folgenden wollen wir daher die Darstellbarkeit
PolynoPkvon homogenen
d
men (mit mehreren Variablen) in der Form P = j=1 Lj , wobei Lj Linearformen sind, untersuchen.
3.3 Quadriken
Wie im Fall ganzer Zahlen P
betrachten wir zunächst den quadratischen Fall.
Es sei also P (x0 , . . . , xn ) = ni,j=0 aij xi xj . Man kann P auch als Produkt
P (x0 , . . . , xn ) = (x0 , . . . , xn ) · A · (x0 , . . . , xn )T
darstellen, wobei A = (aij )ni,j=1 die Koezientenmatrix ist. Der folgende Satz
aus der linearen Algebra gibt uns dann die Lösung unseres Problems:
48
Satz 3.3. Nach einer linearen Koordinatentransformation ist A eine Ma-
trix, die auf der Haupdiagonalen nur Nullen und Einsen und ansonsten nur
Nullen enthält. Mit anderen Worten, P = L21 + · · · + L2k+1 mit k ≤ n.
Beweis: Der symmetrische Gauÿ-Algorithmus (d.h. nach jeder Zeilen-
operation wird dieselbe Operation in den Spalten ausgeführt) liefert in den
komplexen Zahlen das gewünschte Ergebnis.
Beispiel: P (x0 , x1 ) = x20 + 4x0 x1 + 3x21 lässt sich darstellen als (x0 + 2x1 )2 +
(ix1 )2 .
3.4 Der (projektive) Raum der Polynome vom Grad d
Nun betrachten wir homogene Polynome beliebigen Grades. Wir überlegen
uns leicht mit kombinatorischen Argumenten:
¡ ¢
Proposition 3.4. Es gibt n+d
Monome in den Variablen x0 , . . . , xn vom
d
Grad d.
rik.
Beweis: Wir wiederholen zunächst einige Basisresultate der Kombinaton! = 1 · 2 · ... · n
wird benutzt, um die Anzahl aller möglichen Permutationen einer nelementigen Menge zu berechnen. Mit dem Binomialkoezienten
µ ¶
n
n!
=
k
d! · (n − k)!
kann man bestimmen, wie viele Möglichkeiten es gibt, aus einer n-elementigen
Menge k verschiedene Elemente auszuwählen.
Die analoge Frage nach der Anzahl der Möglichkeiten, aus einer n-elementigen
Menge k Elemente auszuwählen, wobei auch mehrfache Auswahl desselben
Elements zugelassen ist, ergibt die Formel
µ
¶
(n + k − 1)!
n+k−1
=
.
k
(n − 1)! · k!
Das Bilden der von Monomen vom Grad d aus den n + 1 Variablen x0 , . . . xn
entspricht einer Auswahl von d Elementen aus (n + 1), wobei ein Element
öfters ausgewählt
werden
¡n+1+d−1
¢ kann. Dies sind also nach den vorherigen Überlegungen genau
Stück.
d
49
¡n+d¢
Zur Abkürzung
setzen
wir
ab
jetzt
N
:=
. Wir können nun ein Pod
P
lynom i0 +···+in =d ai0 ...in xi0 ...in vom Grad d auch als Vektor mit N Koordinaten (. . . , ai0 ...in , . . . ) auassen und somit den Vektorraum CN als Raum der
Polynome vom Grad d interpretieren. Da allerdings für die Darstellung als
Potenzsumme Ld1 + · · · + Ldk konstante Vielfache irrelevant sind, ist es natürlicher, die Polynome als Punkte im projektiven Raum PN −1 zu betrachten
(also den Raum der Geraden in CN durch den Nullpunkt). Die Koezienten
des Polynoms ergeben dann die homogenen Koordinaten [· · · : ai0 ...in : . . . ],
z.B. entspricht x20 + 4x0 x1 + 3x21 dem Punkt [1 : 4 : 3] im P2 .
3.5 Die Veronese-Abbildung
Im Fall von Polynomen höheren Grades d ≥ 3 können wir das WaringProblem auf eine geometrische Fragestellung zurückführen. Dazu interpretieren wir die homogenen Polynome vom Grad¡ d als
¢ Punkte im anen Raum
CN bzw. im projektiven Raum PN −1 (N = n+d
). Eine natürliche Frage ist
d
dann: Welche geometrische Form hat die Teilmenge der Potenzen von Linearformen Ld ?
Man berechnet mit Hilfe der multinomischen Formel
(a0 x0 + · · · + an xd )d =
X
i0 +...in
n
Y
d!
(aj xj )ij ,
i
!
.
.
.
i
!
0
n j=1
=d
Q
d!
ij
dass solche Potenzen Koordinaten der Form [· · · : i0 !...i
j=1n (aj ) : · · · ] im
n!
d!
PN −1 haben. Nach einer koordinatenweisen Stauchung mit dem Faktor i0 !...i
n!
entspricht dies gerade dem Bild der sogenannten Veronese-Abbildung
νd : Pn → PN −1
[a0 : · · · : an ] 7→ [ad0 : · · · : adn ],
wobei die Koordinaten im Bildraum gerade alle Monome vom Grad d durchlaufen.
Beispiel: Ein einfaches Beispiel hierfür ist die rationale Normkurve (auch
verdrehte Kubik genannt):
ν3 : P1 → P3
[a0 : a1 ] 7→ [a30 : a20 a1 : a0 a21 : a31 ].
50
Man sieht übrigens leicht, dass diese Kurve gerade durch die Gleichungen
xw = yz,
xz = y 2 ,
yw = z 2
gegeben ist (wenn [x : y : z : w] die Koordinaten des P3 bezeichnen).
Für allgemeine n, d sind die Bilder von νd (dies sind die sogenannten
Veronese-Varietäten ) komplizierter, aber ebenfalls als Nullstellenmengen
von Polynomen beschreibbar. Die Veronese-Abbildung erweist sich auÿerdem
als eineindeutig. Insbesondere ist das Bild ν(Pn ) ebenfalls n-dimensional.
3.6 Sekantenvarietäten
Der nächste Schritt geht von der natürlichen Frage aus, welche Punkte im
PN −1 Polynomen der Form Ld1 + Ld2 entsprechen. Man rechnet direkt aus,
dass dies gerade die Punkte sind, die auf der Geraden durch die Punkte L1d
und Ld2 liegen. Dasselbe gilt für k + 1 Summanden:
Satz 3.5. Ein Polynom ist als Summe Ld1 + . . . Ldk+1 darstellbar, genau
dann wenn der zugehörige Punkt im PN −1 in dem Raum liegt, der durch die
Punkte Ld1 , . . . , Ldk+1 auf der Veronese-Varietät aufgespannt wird.
Geraden durch zwei Punkte der Menge νd (Pn ) bezeichnet man als Sekanten. Dementsprechend liegt die folgende Denition nahe:
Denition 3.6. Die Sekantenvarietät Seck νd (Pn ) ist die Menge der
Punkte aller k -dimensionalen Räume, die durch k + 1 Punkte auf νd (Pn )
gehen, zuzüglich der Grenzwerte dieser Punkte.
Warum nehmen wir die Grenzwerte hinzu? Dies sind Punkte, die auf
Tangenten der Veronese-Varietät liegen, und bilden in diesem Sinne eine Abschlieÿung der Sekantenräume (wir füllen die Lücken). Man überlegt sich
leicht, dass diese Menge relativ klein ist (es gibt viel mehr Sekanten als Tangenten). Der Vorteil dieser Abschliessung ist, dass dann Seck νd (Pn ) ebenfalls
durch polynomiale Gleichungen im PN −1 beschrieben werden kann.
Durch diese Überlegungen haben wir folgende Modikation des WaringProblems erreicht:
Problem 3.7. Für welche k ist Seck νd (Pn ) = PN −1 ?
51
Dabei ist zu bemerken, dass dies dem groÿen Waring-Problem entspricht, nämlich der Frage, mit wieviel Summanden wir fast alle Polynome
darstellen können (mit Ausnahme der Punkte auf den Tangenten). Wir können die Frage sogar noch etwas weiter vereinfachen. Das Problem ist nämlich
äquivalent zur Gleichheit der Dimension, d.h. wir prüfen
dim Seck νd (Pn ) = N −1?
Warum reicht dies aus? Der Grund ist, dass eine polynomiale Gleichung sofort
die Dimension um 1 reduziert. Wenn also die Dimension der Sekantenvarietät N −1 ist, heisst das nichts anderes, als dass das zugehörige polynomiale
Gleichungssystem leer ist, mit anderen Worten sie ist der ganze Raum PN −1 .
3.7 Dimensionszählung und der Satz von Alexander
und Hirschowitz
Wir überlegen uns nun, welche Dimension die Sekantenvarietät haben kann.
Man überlegt sich schnell die folgende Abschätzung:
Lemma 3.8. dim Seck νd (Pn ) ≤ (k + 1)n + k
Beweis: Wenn wir k + 1 Punkte auf einem n-dimensionalen Raum unab-
hängig voneinander auswählen, entspricht dies (k + 1)n Parametern. Hinzu
kommt die Dimension k des k -ten Sekantenraumes.
Leider kann die Dimension echt kleiner als die rechte Seite werden, zum
Beispiel wenn νd (Pn ) Geraden enthält (dann kommt durch die Sekante keine
Dimension hinzu) oder wenn die Menge zu ach ist (z.B. schon in einem mdimensionalem (m < N −1) projektiven Unterraum des PN −1 enthalten wäre). Dies ist etwa für Quadriken der Fall (Satz 3.3). Dort hatten wir gesehen,
dass wir n + 1 Summanden benötigen. Würde hingegen im Lemma¡ für ¢d = 2
Gleichheit gelten, hätten wir dim Seck ν2 (Pn ) = (k + 1)n + k = n+2
− 1,
2
n+2
also k + 1 = 2 < n + 1.
Dagegen gibt es für höhere Grade das schöne Resultat, dass in fast allen
Fällen Gleichheit gilt.
Theorem 3.9 (Satz von Alexander-Hirschowitz). Sei d ≥ 3. Dann ist
dim Seck νd (Pn ) = min{N −1, (k + 1)n + k }
52
für alle Tripel (n, d, k) mit Ausnahme der vier Fälle
(n, d, k) = (4, 3, 6), (2, 4, 4), (3, 4, 8), (4, 4, 13).
Durch Umstellen folgern wir:
Korollar 3.10. Fast alle homogenen Polynome vom Grad d ≥ 3 in
C[x0 , . . . xn ] lassen sich als Summe Ld1 + · · · + Ldk+1 schreiben, wenn
¡n+d¢
k+1≥
d
(n + 1)
ist, mit Ausnahme der Fälle (n, d) = (4, 3), (2, 4), (3, 4), (4, 4).
In den Ausnahmefällen stellt sich heraus, dass wir mit einem zusätzlichen Summanden auskommen (d.h. 8, 6, 10 bzw. 15). Das k + 1 kommt in
den Summationsindex, da ja einer k -Sekante k + 1 Summanden entsprechen
(etwa im Geradenfall, also bei k = 1, zwei Summanden).
Beispiele:
1. Der einfachste Fall ist die verdrehte Kubik im P3 , also n = 1, d = 3. Wir
erhalten k + 1 = 4/4 = 1, also die Geradensekanten (und -tangenten) der
Kurve füllen den Raum. Daher ist fast jedes homogene Polynom 3. Grades in
zwei Unbekannten als Summe zweier Potenzen darstellbar. Äquivalent dazu
ist die Aussage (wenn wir wieder von homogenen zu inhomogenen Polynomen übergehen, indem wir x0 = 1 setzen), dass fast jedes Polynom in einer
Variablen vom Grad ≤ 3 Summe zweier Kuben von Linearformen ist. Hier
sehen wir auch, dass echte Ausnahmepunkte existieren, denn z.B. x ist nicht
als Summe zweier Kuben darstellbar (siehe 3.1).
2. Im Fall von n = d = 5 und n = 4, d = 6 erhalten wir
¡5+5¢
¡4+6¢
252
210
5
k+1=
=
bzw. k + 1 = 4 =
,
5+1
6
4+1
5
also in beiden Fällen DIE ANTWORT:
42
The End
53
"!#$%&'(&
)(*&
+*,.-/102,43&56,.798
:<;>=@?AB>C'D@E
VX?JI[Z\G9K]AB\KLG9D@S
^_I`;>D@M;baI1c
h N@KLIJYRQTI`;>D#ijI[QTYLMUN@G9?
k G9W';>YRQTI`;>Ddel@DQTN@G9K
m 7Unpoqo',.0'/J,.-rs,.798
h ;>KLG9Dut]IJYLM4N@G9D@v@B\KRw
FHG9IJD@KLIJM4N&OPFHG9KRQTSUORVXWG9KLYLM4N&=@?JG
FHG9IJD@KLIJM4N&OPFHG9KRQTSUORVXWG9KLYLM4N&=@?JG
deG9B\KLf
OPg'B\KLYRQTG9KPORVXWG9KLYLM4N=@?JG
deG9B\KLf
OPg'B\KLYRQTG9KPORVXWG9KLYLM4N=@?JG
deG9B\KLf
OPg'B\KLYRQTG9KPORVXWG9KLYLM4N=@?JG
tG9M4N@D@IJYLMUN@GyxHD@I[Z\G9KLYLI[Q4z
QH^_G9KL?JIJD){
auI[QTf\?JIJG9v|IJ}~Xgd€OPg'B\KLYLM4N=@D@f\YLS9G9DQTKL=@}‚ƒ@„…†*‡‰ˆ
Š a;
QTN@G9}6;
QTIJEbwl@K k M4N@?Jl@YLYLG9?[QTG9M4N@D@B\?JB\f\IJG9D&‹
~€IJG#deKL=@Œ@Œ*GWG9YLM4N'z
wQTIJf>QTGYLIJM4NŽ}I[Qyv@G9KD=@}G9KLIJYLM4N@G9D‘A’\YL=@D@fZqB\D ~€I[“2G9KLG9DqQTI`;>?Jf\?[G9I1O
M4N&=@D@f\G9D){'=@}G9IJD@G9DuS.”_G9IJYRQT=C'f\G9DVXŒG9KT;
QTIJB\D@YRZ\G9KLYRQ4z>KLE>G9KHYLIJ}=@?JI[G9KLG9D#S9=uE>’\D@D@G9D)•
~X;>S9=b”j=@KLv@GjS9=@D'z>M4N@YRQ–;>DbG9IJD@G9}—G9IJDw;>M4N@G9D k M4N';>?[QTEKLG9IJY˜G9IJDde?JG9IJMUN=@D@f\YR™&YRQTG9}šS9=@K k I›O
}=@?`;
QTIJB>DœG9KLYRQTG9?J?[Q{pv';>YLY<IJDyG9IJD@G_~€I[“2G9KLG9DQTI`;
?Jf\?[G9IJM4N=@D@fH=@}f\G.wB\KL}Q”j=@KLv@G>•q2=@K<A’\YL=@D@f
v@G9Kede?JG9IJMUN=@D@fb”j=@KLv@GYLMUN@KLI[QLQs”_G9IJYLGv';>Y€GUcŒ@?JIJS9I[QTGœ=@D@vžv';>YXIJ}Œ@?[I[S9I[QTGœŸ˜=@?JG9KRZ\G9KRw;>N@KLG9D
N@G9KLf\G9?JG9I[QTG.Q•
~X;>D';>M4NE\B>D@DQTGjf\G9S9G9IJf>Q˜”_G9KLv@G9D){v';>YLY%v@IJG]G9KL}I[QLQTG9?›QTG9DbA’\YL=@D@f\G9DYLIJD@DZ\B\?J?YLIJD@v){\”_G9D@D
IJN@KLGe €Wq”–G9IJM4N=@D@f\G9DuZ\B\Duv@G9D#Q4;
QTY4z
MUN@?JIJM4N@G9D|¡G9KRQTG9DG9I[D@f\G9YLMUN@KTz>D@EqQj”–G9KLv@G9DE>’\D@D@G9D)•
€D@YLM4N@?JIJG9¢\G9D@vž”j=@KLv@G9DYLBp”_B\N@?‰v';>Y€GUcŒ@?JIJS9I[QTG;>?JYX;>=@M4Nv';>YXIJ}Œ@?JI[S9I›QTGyŸ˜=@?JG9KRZ\G9KRw;>N@KLG9D
IJDa;
QT?`;>W|IJ}Œ@?JG9}G9DqQTI[G9KRQ{=@}v@IJG£Ÿ˜KLf\G9W@D@IJYLYLGœS9=#Z\G9KT;>D@YLMUN';>=@?JIJM4N@G9D)•
~X;>D@D”j=@KLv@Gv';>Yef\?JG9IJMUN@Gy¤%G9KRw;>N@KLG9Dwl@K£v@IJG k IJ}=@?`;
QTI[B>Dv@G9YœS.”_G9IJYRQT=C'f\G9DŽVXŒ*G9KT;
QTI›O
B\D@YRZ\G9KLYRQ4z>KLE\G9K€;>D@f\G.”–;>D@vQ•
¥\¥
R
1
2
I2
Uin ~
I1
I3
C
3
€W@W@IJ?Jv@=@D@f
*Ÿ˜I[Dw;>MUN@G£i h O k M4N';>?[QT=@D@f
!""#%$'&)(*!"+-,.+/(*+10321+
4!564!564 7 '$98›p&2p;:=<|&9q?>
~€IJG k =@}}G£;>?J?JG9K–IJD#G9IJD@G9}Ae@ D@B>QTG9DuS9=@YT;>}}G9D@?`;>=wG9D@v@G9D
n
X
k QTKL’\}GXIJYRQHf>?JG9IJMUNBH=@?J? •
ik = 0
X~ ;>WG9IN';>W*G9Db;>?J?JG˜ZqB\}-@eD@B>QTG9D”_G9f>wl@N@KLG9D@v@G9D k QTKL’\}G ŒB\YLI[QTI[Z\G9Y¤%B\KLS9G9IJM4N@G9D =@D@vb;>?J?JG
S9=@}C@eD@B>QTG9DuN@IJD3D'IJG9¢\G9D@v@G9D k QTKL’\}GeD@G9f\;
QTI[ZqG9Y]¤%B\KLS9G9I[MUN@G9D)•
k=1
'$98›p&HG')(9(*&9q?>
~€IJG k =@}}G£;>?J?JG9K–S9=uG9IJD@G9K k MUN@?JG9I[wGef>G9N@’\KLG9D@v@G9D k Œ';>D@D&=@D@f>G9DIJYRQjf\?JG9IJM4NIBH=@?J? •
4!564!5FE 7
n
X
vk = 0
k=1
X~ ;>WG9I@N';>WG9DD';
QTl@KL?JIJM4N@G9K<¡G9IJYLG]ŒB\YLI[QTI[Z\G k Œ';>D@D=@D@f\G9DŒB\YLI[QTI[Z\G9Y‰¤%B\KLS9G9IJM4N@G9D=@D@vbD@GUO
fq;
QTI[Z\G k Œ';>D@D=@D@f\G9DD@G9fq;
QTI[Z\G9Y]¤%B\KLS9G9IJM4N@G9D)•
¥KJ
+ +/ 03+103+ , +/ +
€=@Y v@G9D @eIJKLM4N@N@B>“ YLMUN@G9DdeG9YLG.QTS9G9DG9KLf\G.WG9D6YLIJM4Nbwl@K%v';>Y k MUN';>?›Q4W@I[?Jv €W@W)• jwB\?Jf\G9D@v@G
de?JG9IJM4N&=@D@f>G9DH
I1 + I 2
−I2 + I3
−U1 + U2 + U3
U1
R1
I3
0
0
0
Uin
U2
=
I2
dU3
= C
dt
=
=
=
=
€=@Yjv@G9}‚de?JG9IJM4N=@D@f\YLYR™&YRQTG9} G9KLf\IJWQjYLIJM4N|wl@Kjv@IJG@HB\D@v@G9D@YT;
QTB\KLYLŒ';>D@D&=@D@f
U3
J
¥
1
dU3
=
(Uin − U3 )
dt
R1 C 1
^_G9Ijde?JG9IJM4N=@D@f œN';>D@v@G9?[QG9Y YLIJMUNŽ=@} G9IJD@G|~€I[“2G9KLG9DQTI`;>?Jf\?[G9I[M4N&=@D@f@•<~€IJG9YLGIJYRQb;>WG9K
D@IJM4NQ<B\N@D@G ”_G9I[QTG9KLG9Y‰?J’>YTW';
K•~€IJG–;>?J?Jf\G9}bG9IJD@G g'B\KL} G9IJD@G9K<~€I[“2G9KLG9DqQTI`;>?Jf\?[G9IJM4N=@D@f€?`;>=QTG.Q 345
dx
(t) = λx(t) + g(t)
dt
A 2H 03+/( +H +H +
!#" %$
36
'&)(*
87
:9<;
= K !#" +$,
.-
0/ 21
g'KT;>f\GK
¡ JI GXE
;>D@D#}6;>D x (t) = λx(t) + g(t) wl@K–WG9?JIJG9W@IJf\G λ =@D@v#W*G9?JIJG9W@IJf\GXg'=@D@EqQTIJB\D@G9D|f Q
?J’\YLG9D
sv@G9KG BH=@}G9KLIJYLM4N
~X;
wl@K˜”jIJKLvv';>Y%S9=6W*G.QTKT;>MUNqQTG9D@v@GX2G9I[QTIJDQTG9KRZ
;>?J? [t , t ] IJD Z&IJG9?JG]E?JG9IJD@G€2G9I[QTIJDqQTG9KRZ>;>?[?JG
v@G9KHAz>D@f\G h S9G9KL?JG9f>Q•
g<l@K h → 0 f\IJ?[Q x → x(t ) {‰”_B\WG9I x v@G9K6;>Œ@Œ@KLBcIJ}6;
QTI›ZqG6¡G9KRQ=@D@v x(t ) v@G9K
Q4;
QTYTz>M4N@?JIJMUN@GX¡ G9KRQHIJYRQ•
^_G9}G9KLE=@D@f WG9YLI[QTS.QHG9IJD@GeG9IJD@v@G9=QTIJf\G£A’\YL=@D@f@{@w;>?J?JY x(0) = x IJYRQ{”_B\WG9I x ∈ R
G9IJD@GeWG9?JIJG9W@IJf\G>(7){@;>WG9K]wG9YRQTG£KLG9G9?J?JGœ);>N@?)IJYRQ•
:˜KLB\W@?JG9I} ¡ IJKyYL=@M4N@G9D‘v@IJG6G9IJD@v@G9=QTIJf\G|A’\YL=@D@fWG9I Z\B\KLf\G9f\G9WG9D@G9} x S9= v@G9D 2G.I[QRO
0
>=
?
0
1
1
end
1
1
0
0
¥
0
#
Œ@=@D@EqQTG9D
t1 , t2 , t3 , ..., tend
x0 (0) =
=
0
x (t1 ) =
≈
¡ IJK]W*G9KLG9MUN@D@G9D €Œ@Œ@KLBpcIJ};
QTIJB\D@G9D
WG9I
x0
wl@K
x(tn )
}I[Q]FHIJ?[wG€ZqB\D
xn − xn−1
= λxn−1 + g(tn−1 )
h
YRQ4;>KRQTG9D@v)•
⇔
xn −xn−1
h
xn
λx(0) + g(0)
λx0 + g(0)
λx(t1 ) + g(t1 )
λx1 + g(t1 )
xn = xn−1 + h(λxn−1 + g(tn−1 ))
IJYRQjv@G9KH~€I[“2G9KLG9D@S9G9D =@B>QTIJG9DqQ€=@D@vuv';>N@G9Kjf\IJ?[Q xn −xn−1
h
≈ x0 (tn−1 )
¡ IJK]W*G.QTKT;>MUNqQTG9DuwB\?Jf\G9D@v@G£~€I[“2G9KLG9DqQTI`;>?Jf\?[G9I[MUN=@D@f
) ?> 4 g<l@K RG9v@G9Y x ²R GUcIJYRQTIJG9KRQ€;>=w‰v@G9} G9D@v@[email protected] sDqQTG9KRZ>;>?J?
A’\YL=@D@f x \Z B\D U{@v';>YjN@G9IJ¢>Q{
x0 (t) = λx(t) + g(t)
>?
0
x0 (t) = λx(t) + g(t)
[t0 , tend ]
∀t²[t0 , tend ]
}I[Q€v@G9Ke €Dw;>D@f\YLW*G9v@IJD@f\=@D@f ) = x {Z\B\KLKT;>=@YLf\G9YLG.QTS.Q{ v';>YTY
f\IJ?[Q_wl@Kjv@IJG£A’\YL=@D@f@{ x(t) IJYRQjx(t
YRQTG.QTIJfbv@I[“[email protected]';>K9•
0
g(t)
0
f\G9D';>=G9IJD@G
YRQTG.QTIJf|IJYRQ• k B>}I[Q
~€G9K k ;
QTS e”jIJKLv#N@IJG9K]D@IJMUNqQjWG.”jIJG9YLG9D)•
)?> E k G9I ;>=w
YRQTG.QTIJf6=@D@vv@I[G k M4N@KLI[QLQP”_G9I[QTG N@IJD@KLG9IJM4N@G9D@vžE?JG9IJD)•~X;>D@D
f\IJ?[Q£wl@Kv@IJG6G9gIJD@v@G9=[tQTIJf\,Gt A’\]YL=@D@f x(t) Z\B\D £}I[Q x(t ) h= x =@D@vŽv@IJG6D=@}G9KLIJYLMUN@G
A’\YL=@D@fbZ\B\D Ÿ˜YjGUcIJYRQTIJG9KRQjG9IJD@G @HB\D@YRQ4;>DqQTG c > 0 0
end
0
0
max | x(tn ) − xn |≤ ch
”_B\WG9I c =@D';>W@N'z>D@f\IJfZqB\D
n=1,...,N
N
I[YLQ• N YLG9Iv@IJGe €D@S;>N@?v@G9KjtG9IJ?JIJDqQTG9KRZ>;>?J?[G>•
¥
EH564!564
&
xn − xn−1
= λxn−1 + g(tn−1 )
h
x0 (tn−1 = λx(tn−1 ) + g(tn−1 )
(9) ⇒
4!5 a;>DuW@[email protected]@IJGœ~€I[“2G9KLG9D@Sœ;>=@YHv@G9K]¤%G9KRw;>N@KLG9D@YLf\?JG9IJM4N&=@D@f _=@D@vuv@G9K€~€I[“2G9KLG9DqQTI›O
;>?Jf\?JG9I[M4N&=@D@f IJ}:˜=@D@EqQ t U•
t=tn−1
~X;>D@Duf\IJ?[Q_wl@Kjv@G9Duf\?JB\W';>?JG9D#g'G9N@?JG9K
n−1 en := xn − x(tn )
en = (1 + λh)en−1 + hrn
rn
EH5
JI YRQjv@G9Kj?JB\E
;>?JGe~€IJYLEKLG.QTIJYLIJG9KL=@D@f\YRwG9N@?JG9K9•
~€=@KLM4NKLG9E=@KLYLI[Z\G9YH €=3D'’\YLG9DG9KLN'z>?[Qj}6;
D
en = (1 + λh)n e0 +
n−1
X
(1 + λh)i hrn−i
i=0
e0 = x0 − x(t0 ) = 0
n−1
X
⇒ en =
|1 + λh|i hrn−i
H5 ~€KLG9IJG9M4EYL=@D@f\?JG9IJM4N=@D@f6=@D@vut<;™&?JB\KLG9DqQP”jIJM4E?J=@D@f
Ÿ˜YjGUcIJYRQTIJG9KRQjG9IJD@GH@ B\D@YRQ4;>DqQTG c > 0 {'YLBv';>YLY max|r | < ch •
i=0
n
n
=⇒
Dreiecksungleichung
5¡
n−1
X
| en |≤ ch
(1 + λh)i = ch2
2
i=0
max | eN |≤ ch
N
IJK–D&=QTS9G9D
N h = t n − t0
M9N#w;>?J?JY
max | en |≤ n
| 1 + λh |> 0
2
(
(
v)• N)•
n
wl@K
N
wl@K
YLB\D@YRQ
| 1 + λh |= 0
|1+λh|N −1
|1+λh|−1
h<
YLB\D@YRQ
| 1 + λh |= 0
|1+λh|n −1
|1+λh|−1
−1
λ
wl@K
λ<0
,
G<)>`&ep '&
¡ IJK]W*G.QTKT;>MUNqQTG9Dv@G9D:˜=@D@EqQ t
EH564!5FE
n
x0 (tn ) = λx(tn ) + g(tn )
x(tn ) − x(tn−1 )
≈
h
¥
~X;>KT;>=@YjG9KLf\IJWQjYLIJM4Nuv';>[email protected]@G9=@G9Yj¤%G9KRw;>N@KLG9D
s}Œ@?JIJS9I›QTG9YjŸ˜=@?[G9KRZqG9KRw;>N@KLG9DH
xn − xn−1
= λxn + g(tn )
h
?
xn =
#%*03+/ +"+/( 21 03+
5
g(tn )h + xn−1
1 − hλ
36
+H( +/21# +
;
" + + 9
deKT;>Œ@N#v@G9YHGUcŒ@?JI[S9I[QTG9D#=@D@vuIJ}Œ@?JI[S9I›QTG9D#Ÿ˜=@?JG9KLY]wl@K]Z\B\[email protected]'D@IJG9KRQTG
h
1
h=0.001, λ=−50
0
−1
−2
−3
−4
Expl.E
Impl.E
−5
0
0.1
0.2
0.3
0.4
0.5
J
0.6
0.7
0.8
0.9
1
6
4
2
0
−2
−4
Expl.E
Impl.E
h=0.04, λ=−50
−6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
20
h=0.041, λ=−50
15
10
5
0
−5
−10
−15
−20
Expl.E
Impl.E
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
˜Ÿ Y€IJYRQ€S9=žG9KLE\G9D@D@G9D){2v';>YLY€v';>Y€GUcŒ@?JIJS9I[QTGyŸ˜=@?JG9KRZ\G9KRw;>N@KLG9D){WG9If\KL’\¢\G9KLG9} h {*D@IJMUNqQ€v@G9D
deKT;>Œ@N G9IJD@G9K#Ÿ<cŒB\D@G9DqQTI`;>?[w=@D@EqQTIJB\D ?JIJG.wG9KRQ{_v@G9K|v@G9D k Œ';>D@D=@D@f\YT;>Ww;>?J?Xl@W*G9K#G9IJD@G9}
@HB\D@v@G9D@YT;
QTB\Kœv';>KLYRQ4G.?J?[Q•Ÿ˜YyIJYRQœIJ} S.”_G9I[QTG9D ~€I`;>f\KT;>}} G9IJD@GbS.”jIJYLMUN@G9D O ¥ =@D@v ¥ B\YPO
S9IJ?J?JI[G9KLG9D@v@G#g'=@D@EqQTIJB\D)• s} v@KLI[QLQTG9D ~€I`;>f\KT;>}} B\YLS9IJ?[?JI[G9KRQbv@G9KdeKT;>Œ@N‘=@D@v v@I[Z\G9KLf\IJG9KRQ
;>=@¢\G9KLv@G9}u•~X;>YyIJ}Œ@?[I[S9I[QTGbŸ˜=@?JG9KRZ\G9KRw;>N@KLG9D ?JIJG.wG9KRQœv';>f\G9f>G9D v@G9D deKT;>Œ@N G9IJD@G9KyŸ<cŒB
O
D@G9DqQTI`;>?[w=@D@EqQTIJB\D)•&~X;yD&=@K_v@G9K]:<;>KT;>}G.QTG9K h ZqG9KTz>D@v@G9KRQ–”j=@KLv@G>{E
;>D@D|}6;>D;>D@D@G9N@}G9D){
?
J
v';>YLY v@IJGHdeKL’\¢\G–ZqB\D h v@G9D¤˜G9KL?`;>=w)v@G9Y_deKT;>Œ@N@G9Dv@G9Y GUcŒ@?JIJS9I[QTG9DŸ˜=@?JG9KLY G9DqQTYLM4N@G9IJv@G9D@v
WG9G9IJD3D'=@YLYRQ•
}I[Q λ < 0
x = λx
0
2
1.5
1
0.5
0
−0.5
−1
−1.5
−2
0
<g l@Kjv@IJG£A’\YL=@D@f
Ÿ<cŒ@?JIJS9I[QTG9K]Ÿ˜=@?JG9K
0.5
1
1.5
f\IJ?[Q 3
⇒
xn = (1 + λh)xn−1
2
2.5
x(t) = x(0)eλt
xn − xn−1
= λxn−1
h
3.5
4
|x(t)|
4.5
5
IJYRQj}B\D@B>QTB\D|w;>?J?[G9D@v)•
˜Ÿ Yjf\IJ?[Q |x | < |x | D=@K]wl@K |1 + λh| < 1 •
N;>?JY k M4N@KLI[QLQs”_G9I[QTG£IJYRQjIJ}}bG9K–ŒB\YLI[QTI[Z{ λ D@G9fq;
QTI[Z•
n
n−1
|1 + λh| < 1
s}Œ@?JIJS9I›QTG9K]Ÿ˜=@?JG9K
⇔
1 + λh < 1
∧
⇔
λh < 0
2
h<− ,
λ
∧
1 + λh > −1
v)• N)•*D=@K]wl@K
h < − λ2 .
?
Ÿ˜Yjf\IJ?[Q
xn − xn−1
= λxn
h
|xn | < |xn−1 |
wl@Kj;>?J?JG
h>0
1
1
=
1 − λh
1+ε
⇒
{'v@G9D@D
<1
xn =
}I[Q
1
xn−1
1 − λh
ε := −λh > 0
X~ ;>YIJ}Œ@?[I[S9I[QTGŸ˜=@?JG9KRZqG9KRw;>N@KLG9D G9KLS9G9=@f>Q IJ}}G9Kœ;>W@E?JIJD@f\G9D@v@GA’\YL=@D@f\G9DŽ=@D';>W@N'z>D@f\IJf
Z\B\Duv@G9K k M4N@KLI[QLQP”_G9I[QTG>•
J
K /
C1
U
in
1
1
+
−
R1
" 2
6$ -
C2
3
$ "
R2
4
−
−
+
+
I1
I2
U0 = 0
B€;>M4Nuv@G9}C@eIJKLMUN@N@B>“
k Œ';>D@D=@D@f\G9DH
YLM4N@G9D k QTKLB\}f\G9YLG.QTS£f\IJ?[Q −IC1 + IR1
−I1 + IC2 − IR1
−IC2 + IR2
−IR2 − IR2 − I2
IC 1 + I V
V R1
V R2
V C1
V C2
=
=
=
=
=
=
=
=
=
0
0
0
0
0
U1 − U2
U3 − U4
U5 − U1
U2 − U3
Ÿ˜?JG9}G9DqQTWG9S9B\f\G9D@Gyde?JG9IJMUN=@D@f\G9D
dVC1
dU5 dU1
= C1 (
−
)
dt
dt
dt
dU2 dU3
dVC2
C2
= C2 (
−
)
dt
dt
dt
V R1
U1 − U 2
=
R1
R1
V R2
U3 − U 4
=
R2
R2
−AU1
−AU3
Uin
IC 1 = C 1
IC 2 =
IR 1 =
IR 2 =
U2 =
U4 =
U5 =
J
Ÿ˜YjG9KLf\IJWQ]YLIJM4N){@D';>M4Nu}G9N@KLG9KLG9DuxH}bwB\KL}=@D@f\G9D){G9IJDde?JG9IJM4N=@D@f\YLYR™&YRQTG9}}I[Q]v@G9D#WG9I›O
v@G9DxHDWG9E
;>D@DqQTG9D U =@D@v U 1
3
dUin dU1
−
)+
dt
dt
d(AU1 ) dU3
−C2 (
−
)+
dt
dt
−C1 (
⇐⇒
(
⇐⇒
(
1
(U1 (A + 1)) = 0
R1
1
(U3 (A + 1)) = 0
R2
dU1
= − R1+a
U1 + dUdtin
dt
1 C1
1
3
A dU
U3
+ dU
= − R1+A
dt
dt
2 C2
0
U10 = − R1+A
+ Uin
1 C1
0
U3 + A R1+A
U1 − AUin
U30 = R1+A
2 C2
1 C1
¶
¶µ ¶ µ
µ 0¶ µ
g1 (t)
U1
b1 b2
U1
+
=
g2 (t)
U3
U30
b3 b4
⇐⇒
→
−
−
−
x 0 = B→
x +→
g (t)
}I[Q
{
b3
{
1+A
0
b2 = 0 g1 (t) = Uin
(t)
R1 C 1
1+A
1+A
0
=A
b4 =
g2 (t) = −AUin
(t)
R1 C 1
R2 C 2
b1 = −
{
Ÿ<cŒ@?JIJS9I[QTG9YjŸ˜=@?JG9KRZ\G9KRw;>N@KLG9D#wl@K k ™&YRQTG9}GK
{
−
→−→
−
x
x n−1
n
−
−
= B→
x n−1 + →
g (tn−1 )
h
→
−
−
−
xn =→
x n−1 + hB + h→
g (tn−1 )
s}Œ@?JIJS9I›QTG9YjŸ˜=@?[G9KRZqG9KRw;>N@KLG9D#wl@K k ™&YRQTG9}GK
?
→
−
−
xn−→
x n−1
−
−
= B→
xn+→
g (tn )
h
→
−
−
−
−
x n − hB →
xn =→
x n−1 + h→
g (tn )
→
−
→
−
→
−
LGS → (I − hB) x n = x n−1 + h g (tn )
→
−
−
−
x n = (I − hB)−1 (→
x n−1 + h→
g (tn ))
J
. I /
; $ $
/
" 6$ -
!
$ "
K /
1
Expliziter Euler
0.2
h=0.001, ω=10, C1=1e−07, C2=1e−07
U1
U2
Uout
U3
Uin
0.15
0.1
0.05
0
−0.05
−0.1
−0.15
−0.2
0
0.5
1
1.5
2
2.5
Expliziter Euler
2
h=0.00175, ω=20, C1=1e−07, C2=1e−07
1.5
U1
U2
Uout
U3
Uin
1
0.5
0
−0.5
−1
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
€~ IJGjB\W@IJf\G9DW*G9IJv@G9D|deKT;
C'E>G9D6S9G9IJf\G9D){qv';>YLY_v@G9K%GUcŒ@?JIJS9I[QTGHŸ˜=@?[G9K%wl@K%E?JG9IJD@G k M4N@KLI[Qs”]”_G9I›O
QTG9D£Z\G9KLD&l@DwQTIJf\G%A’\YL=@D@f\G9D){pwl@Kf\KLB\¢\G k MUN@KLI[QLQs”_G9I[QTG9Dy;>W*G9K=@D@YLIJD@D@IJf\G%A’\YL=@D@f\G9Dœ?JIJG.wG9KRQ•
Jq¥
~X;>YjIJ}Œ@?JI[S9I›QTGeŸ˜=@?JG9KRZ\G9KRw;>N@KLG9DuN@IJD@f\G9f\G9D#?JIJG.wG9KRQj;>=@M4N#wl@K]f\KL’\¢\G9KLG k MUN@KLI[QLQs”_G9I[QTG9D|ZqG9KPO
Dl@DwQTIJf\GHA’\YL=@D@f\G9D)• sD@YLWG9YLB\D@v@G9KLGXYLIJG9NqQ_}6;>DbIJDv@G9D6D'z>MUN@YRQTG9DW*G9IJv@G9D6 €W@W@IJ?Jv@=@D@f\G9D){
v';>YLYeYLIJM4Nv@IJGbVX=QTŒ@=QTYLŒ';>D@D&=@D@f U = U Z\G9KLv@B\Œ@ŒG9?[Q{2”_G9D@D}6;>Dv@I[G g'KLG =@G9D@S ω
v@G9Y€Ÿ˜I[D@fq;>D@f\YLYLIJf\D';>?JY_ZqG9KLv@B\Œ@Œ*G9?[Q•
?
out
4
Impliziter Euler
0.2
h=0.001, ω=10, C1=1e−07, C2=1e−07
U1
U3
U2
Uout
Uin
0.15
0.1
0.05
0
−0.05
−0.1
−0.15
−0.2
0
0.5
1
1.5
2
2.5
Impliziter Euler
0.4
h=0.001, ω=20, C1=1e−07, C2=1e−07
U1
U3
U2
Uout
Uin
0.3
0.2
0.1
0
−0.1
−0.2
−0.3
−0.4
0
0.2
0.4
0.6
0.8
JJ
1
1.2
1.4
Die Unlösbarkeit der Gleichung fünften Grades durch Radikale
Teilnehmer:
Max Bender
Marcus Gawlik
Anton Milge
Leonard Poetzsch
Gabor Radtke
Miao Zhang
Andreas-Oberschule
Georg-Forster-Oberschule
Georg-Forster-Oberschule
Georg-Forster-Oberschule
Georg-Forster-Oberschule
Andreas-Oberschule
Gruppenleiter:
Jürg Kramer
Humboldt-Universität zu Berlin,
Mitglied im DFG-Forschungszentrum Matheon
Mathematik für Schlüsseltechnologien“
”
Die Gruppe beschäftigte sich mit der Frage nach der Lösbarkeit der allgemeinen Gleichung fünften Grades durch Radikale. Zunächst wurde dazu
festgestellt, dass lineare, quadratische, kubische und quartische Gleichungen
durch Radikale lösbar sind.
Mit Hilfe von N.-H. Abels Originalarbeit aus dem 19. Jh. erarbeitete sich die
Gruppe dann das Ergebnis, dass die allgemeine Gleichung fünften Grades
nicht durch Radikale lösbar ist.
Dazu musste sich die Gruppe einige Grundlagen der Gruppen- sowie der
Körpertheorie erarbeiten. Speziell spielte das Verständnis der symmetrischen
Gruppe S5 von fünf Elementen eine wichtige Rolle.
13
Die Unlösbarkeit der allgemeinen Gleichung
fünften Grades durch Radikale
1
Einleitung
Die allgemeine Gleichung eines Polynoms n-ten Grades mit den Koeffizienten
σ1 , . . . , σn lautet
f (X) = X n − σ1 X n−1 ± . . . + (−1)n−1 σn−1 X + (−1)n σn .
Nach dem Fundamentalsatz der Algebra besitzt ein solches Polynom genau
n Nullstellen x1 , . . . , xn ∈ C. Somit lässt sich die Funktion eindeutig als
Produkt ihrer Linearfaktoren darstellen
f (X) = (X − x1 ) · (X − x2 ) · . . . · (X − xn ).
Nach dem Vietaschen Wurzelsatz ergeben sich folgende Zusammenhänge zwischen den Nullstellen x1 , . . . , xn und den Koeffizienten σ1 , . . . , σn
σ1 = σ(x1 , . . . , xn ) =
x 1 + . . . + xn ,
σ2 = σ(x1 , . . . , xn ) = x1 · x2 + x1 · x3 + . . . + xn−1 · xn ,
..
.
σn = σ(x1 , . . . , xn ) =
x1 · x2 · . . . · xn .
Aufgrund ihrer Symmetrie verändern sich die Werte dieser Funktionen beim
Vertauschen (Permutieren) der Variablen nicht. Sie werden deshalb die elementarsymmetrischen Polynome in den Variablen x1 , . . . , xn genannt. Von
großer Bedeutung für den sich später ergebenden Widerspruch ist, dass die
x1 , . . . , xn als variabel vorausgesetzt werden. Das bedeutet, dass keine algebraischen Zusammenhänge zwischen den Variablen x1 , . . . , xn bestehen dürfen.
Als Vorbereitung auf die nachfolgende, grundlegende Definition betrachten
wir das Beispiel einer quadratischen Gleichung, d.h.
X 2 − σ1 X + σ2 = 0.
(1)
Die beiden Lösungen dieser Gleichung lassen sich mithilfe der p, q-Formel
berechnen zu
s
σ1
σ12
±
− σ2 .
x1,2 =
2
4
14
Dabei sieht man, dass die auftretenden Funktionen p = σ1 /2 und R =
σ12 /4 − σ2 rationale Funktionen (in diesem Fall sogar Polynome) in den elementarsymmetrischen Polynomen σ1 , σ2 sind.
2
Die Problemstellung
Für die Fortführung ist es zunächst wichtig, einige Bezeichnungen einzuführen.
Dazu sei C[x1 , . . . , xn ] die Menge der Polynome in x1 , . . . , xn mit komplexen
Koeffizienten. Ein Quotient zweier Polynome P, Q ∈ C[x1 , . . . , xn ] heißt rationale Funktion. Entsprechend bezeichnen wir mit
(
C(x1 , . . . , xn ) :=
P
Q
¯
)
¯
¯
¯ P, Q ∈ C[x1 , . . . , xn ]
¯
den Körper aller rationalen Funktionen in den n Variablen x1 , . . . , xn . Analog
sei C[σ1 , . . . , σn ] die Menge der Polynome in σ1 , . . . , σn bzw. C(σ1 , . . . , σn ) der
Körper der rationalen Funktionen in σ1 , . . . , σn . Wir haben
C[σ1 , . . . , σn ] ⊆ C[x1 , . . . , xn ]
und
C(σ1 , . . . , σn ) ⊆ C(x1 , . . . , xn ).
Im Beispiel (1) wurde ein Polynom zweiten Grades mit der p, q-Formel gelöst.
Dabei ergab sich die Form
√
x1 = p + R
(2)
mit p, R ∈ C(σ1 , σ2 ). Wir stellen uns nun die Frage, ob i.A. die Nullstellen von
f durch solche Radikale darstellbar sind. Die Form der Gleichung (2) und die
Cardano-Formeln für Polynome dritten und vierten Grades motivieren dabei
die folgende Definition.
Definition. Eine Nullstelle x = xj heißt durch Radikale darstellbar, falls es
ein m ∈ N und rationale Funktionen R, p, p1 , . . . , pm−1 ∈ C(σ1 , . . . , σn ) gibt,
so dass
³ √ ´m−1
√
m
m
R
x = p + p1 R + . . . + pm−1
√
gilt; dabei gilt m R ∈
/ C(σ1 , . . . , σn ).
15
Wir können folgende Vereinfachungen erreichen:
• p1 = 1.
• m eine Primzahl.
Ersetzt man nämlich R durch R/pm
1 , so erhält man p1 = 1 und verändert die
Voraussetzungen nicht. Auf den Fall m = Primzahl sind wir geführt, indem
wir eine Iteration der obigen Darstellung vornehmen.
Annahme. Um herauszufinden, ob die Nullstellen von f als Radikale darstellbar sind, treffen wir die Annahme, dass die Gleichung f (X) = 0 eine
solche Lösung besitzt. Nach der ersten Vereinfachung ist die angenommene
Lösung also von der Form
³ √ ´m−1
√
m
m
x1 = p + R + . . . + pm−1
R
.
Im Weiteren wird es unser Ziel sein, einen Widerspruch zu dieser Annahme
herzuleiten.
3
Der erste Beweisschritt
Wir schränken nun auf den Fall n = 5 ein; außerdem erinnern wir uns daran,
dass m eine Primzahl ist. Wir nehmen also an, dass unsere Ausgangsgleichung
f (X) = 0 eine Lösung der Form
³ √ ´m−1
√
m
m
x1 = p + R + . . . + pm−1
R
(3)
besitzt.
Bevor wir im ersten Beweisschritt fortfahren, haben wir noch die m-ten Einheitswurzeln ζ j einzuführen; dabei ist
µ
ζ = e2πi/m = cos
¶
µ
2π
2π
+ i · sin
m
m
¶
und j = 0, . . . , m − 1 ist. Wir erinnern daran, dass die m Einheitswurzeln
1, ζ, ζ 2 , . . . , ζ m−1 im Einheitskreis der komplexen Ebene (mit dem Ursprung
als Zentrum) ein regelmäßiges m-Gon einbeschreiben.
16
Nach langwierigen Überlegungen, welche aber im wesentlichen nur Methoden
der Linearen Algebra und die Berechnung des größten gemeinsamen Teilers
von Polynomen benötigen, stellen wir fest, dass mit der Lösung (3) gleichzeitig auch
x2 = p + ζ
..
.
√
m
³ √ ´m−1
m
R + . . . + pm−1 ζ
xm = p + ζ m−1
√
m
R
³
R + . . . + pm−1 ζ m−1
´m−1
√
m
R
Lösungen der Ausgangsgleichung f (X) = 0 sind. Diese stellen sich als paarweise verschieden heraus, d.h. wir haben somit m verschiedene Lösungen der
Ausgangsgleichung. Da nun aber f (X) ein Polynom vom Grad n = 5 ist,
kann es höchstens 5 verschiedene Nullstellen haben, d.h. wir haben m ≤ 5.
Da m aber eine Primzahl ist, haben wir den Beweis auf die Fälle
m = 2, m = 3, m = 5
reduziert. Diese gilt es im Folgenden zu untersuchen. Dabei beschränken wir
uns hier auf die Betrachtung des Falls m = 5; der Fall m = 2 lässt sich
analog behandeln. Schließlich lässt sich zeigen, dass der Fall m = 3 gar nicht
auftreten kann.
4
Der zweite Beweisschritt
Wir gehen aus von den m Gleichungen
x2
..
.
√
m
³ √ ´m−1
m
R + . . . + pm−1
R
,
³ √ ´m−1
√
m
m
= p + ζ R + . . . + pm−1 ζ R
,
x1 = p +
xm = p + ζ m−1
√
m
³
R + . . . + pm−1 ζ m−1
´m−1
√
m
R
.
Indem wir
y1 = p, y2 =
√
m
R, y3 = p2
³ √ ´2
m
R
17
, . . . , ym = pm−1
³ √ ´m−1
m
R
setzen, erhalten wir das lineare Gleichungssystem
y1 +
y1 +
..
.
y2
ζy2
+
+
y3
ζ 2 y3
+ ... +
+ ... +
ζ
ym
m−1
ym
=
=
x1
x2
2
y1 + ζ m−1 y2 + ζ 2(m−1) y3 + . . . + ζ (m−1) ym = xm .
Nach der bekannten Theorie der linearen Gleichungssysteme sind die Lösungen y1 , y2 , . . . , ym gegeben als Quotienten von Polynomen in den Koeffizienten des Gleichungssystems, d.h. y1 , y2 , . . . , ym sind rationale Funktionen in
x1 , x2 , . . . , xn . Insbesondere stellen wir fest
√
m
R ∈ C(x1 , . . . , xn ).
Zum Beispiel berechnet man im Fall m = 3 leicht
√
3
5
R=
x1 + ζ 2 · x2 + ζ · x3
.
3
Der dritte Beweisschritt
Die symmetrische Gruppe Sn vom Index n ist definiert als die Menge aller
Permutationen von n Elementen. Eine Permutation π ist dabei einfach eine
Anordnung der n Elemente, wobei jedes Element in der neuen Anordnung
genau einmal vorkommen soll und je zwei verschiedenen Elementen auch zwei
verschiedene Bildelemente zugeordnet werden. Wir können sie also auch als
injektive Abbildung der Menge der n Elemente auf sich selbst auffassen.
Eine Permutation ist also insbesondere bijektiv. Wir arbeiten im Folgenden
mit den natürlichen Zahlen von 1 bis n als Elementen. Diese Permutationen
finden ihre Anwendung nun bei Polynomen und rationalen Funktionen in den
n Variablen x1 , . . . , xn . Wir lassen dabei eine Permutation auf die Indizes
wirken. Sei also π ∈ Sn eine Permutation. Dann definieren wir
g π (x1 , . . . , xn ) := g(xπ(1) , . . . , xπ(n) ),
wobei g ∈ C(x1 , . . . , xn ) ist. Nun definieren wir weiter die ”Wertemenge” von
g durch
W (g) := {g π | π ∈ Sn } .
18
Eine rationale Funktion g mit W (g) = {g}, also |W (g)| = 1, nennen wir eine
symmetrische rationale Funktion. Man überzeugt sich leicht davon, dass man
Permutieren und Addieren bzw. Multiplizieren vertauschen kann, da diese
beiden Prozesse völlig unabhängig voneinander sind. Induktiv erhält man
dann, dass dies sogar für mehrere Summanden und Faktoren einer Summe
bzw. eines Produkts gilt. Als Spezialfall, bei dem die Faktoren alle gleich
sind, erhalten wir somit folgendes Vertauschungsgesetz für Potenzen:
(g π )r = (g r )π
(r ∈ N).
Daraus folgt insbesondere für r = m = 5
π 5
³
(g ) = g
´
5 π
=
µ³ √ ´ ¶π
5
5
R
= Rπ = R.
Letzteres Gleichheitszeichen
³ √ gilt
´π wegen der Voraussetzung R ∈ C(σ1 , . . . , σn ).
√
5
5
Somit ist wie R auch
R eine Lösung der Gleichung
z 5 − R = 0.
Diese Lösungen sind aber als fünfte Wurzeln alle von der Form
√
5
zj = ζ j · R (j ∈ {0, . . . , 4}).
Daraus folgt also
³ √ ´π
5
R
= ζj ·
√
5
R
mit einem j ∈ {0, . . . , 4}. Mithilfe von etwas Gruppentheorie (Operationen,
Bahnen und Stabilisatoren) kann man zeigen, dass auch wirklich jedes der
zj (j = 0, . . . , 4) als Bild angenommen wird, d.h. dass es zu jedem dieser zj
auch wirklich eine Permutation π ∈ Sn gibt mit
³ √ ´π
√
5
5
R = ζ j · R.
Somit folgern wir aus den obigen Überlegungen und dem letzten Argument,
dass
n√
o
³√ ´
√
√
5
5
5
5
R =
R, ζ · R, . . . , ζ 4 · R
W
¯ ³ √ ´¯
¯
¯
gilt und erhalten dann ¯W 5 R ¯ = 5.
19
6
Der Widerspruch
Wir erinnern zunächst nochmals daran, dass wir mit der allgemeinen Gleichung fünften Grades arbeiten, d.h. wir nehmen an, dass die Nullstellen
x1 , . . . , x5 unabhängige Variablen sind, also keiner algebraischen Gleichung
(mit komplexen Koeffizienten) genügen.
Ohne Beweis zitieren wir den folgenden Satz.
Satz. Ist g ∈ C(x1 , . . . , x5 ) eine rationale Funktion mit der Eigenschaft
|W (g)| = 5, so ist g (ohne Beschränkung der Allgemeinheit) von der Form
g = g(x1 , . . . , x5 ) = q0 + q1 · x1 + q2 · x21 + q3 · x31 + q4 · x41
mit symmetrischen Funktionen q0 , q1 , . . . , q4 ∈ C(σ1 , . . . , σ5 ).
√
Nach dem zweiten Beweisschritt
ist 5 R ∈ C(x1 , . . . , x5 ). Da nach dem dritten
√
Beweisschritt weiter |W ( 5 R)|
√ = 5 gilt, können wir den vorhergehenden Satz
anwenden. Wir finden, dass 5 R die Gestalt
√
5
R = q0 + q1 · x1 + q2 · x21 + q3 · x31 + q4 · x41
hat, wobei q0 , q1 , . . . , q4 ∈ C(σ1 , . . . , σ5 ) sind.
Wir wenden nun die Permutation
Ã
π=
1 2 3 4 5
2 3 4 5 1
!
√
auf die rationale Funktion 5 R an und erhalten
³ √ ´π
³
´π
5
R
= q0 + q1 · x1 + q2 · x21 + q3 · x31 + q4 · x41
= q0π + q1π · x2 + q2π · x22 + q3π · x32 + q4π · x42
= q0 + q1 · x2 + q2 · x22 + q3 · x32 + q4 · x42 ;
dabei haben wir insbesondere beachtet, dass xπ1 = x2 ist und dass die Funktionen q0 , q1 , . . . , q4 symmetrisch sind.
20
Nach dem dritten Beweisschritt wissen wir andererseits, dass ein j ∈ {0, . . . , 4}
existiert, so dass
³ √ ´π
√
5
5
R = ζj · R
gilt. Zusammen mit der vorhergehenden Rechnung erhalten wir somit die
Relation
q0 + q1 · x2 + q2 · x22 + q3 · x32 + q4 · x42 =
ζ j · q0 + ζ j · q1 · x1 + ζ j · q2 · x21 + ζ j · q3 · x31 + ζ j · q4 · x41 .
Zusammengenommen genügen x1 , . . . , x5 somit der polynomialen Gleichung
q0 (1 − ζ j ) + q1 (x2 − ζ j · x1 ) + q2 (x22 − ζ j · x21 ) +
q3 (x32 − ζ j · x31 ) + q4 (x42 − ζ j · x41 ) = 0 .
Dies stellt aber einen Widerspruch zur angenommenen algebraischen Unabhängigkeit der Variablen x1 , . . . , x5 dar.
Damit ist – zumindest im Fall m = 5 – gezeigt, dass die allgemeine Gleichung
fünften Grades sich nicht mithilfe von Radikalen lösen lässt.
21