Stochastik - schule.at

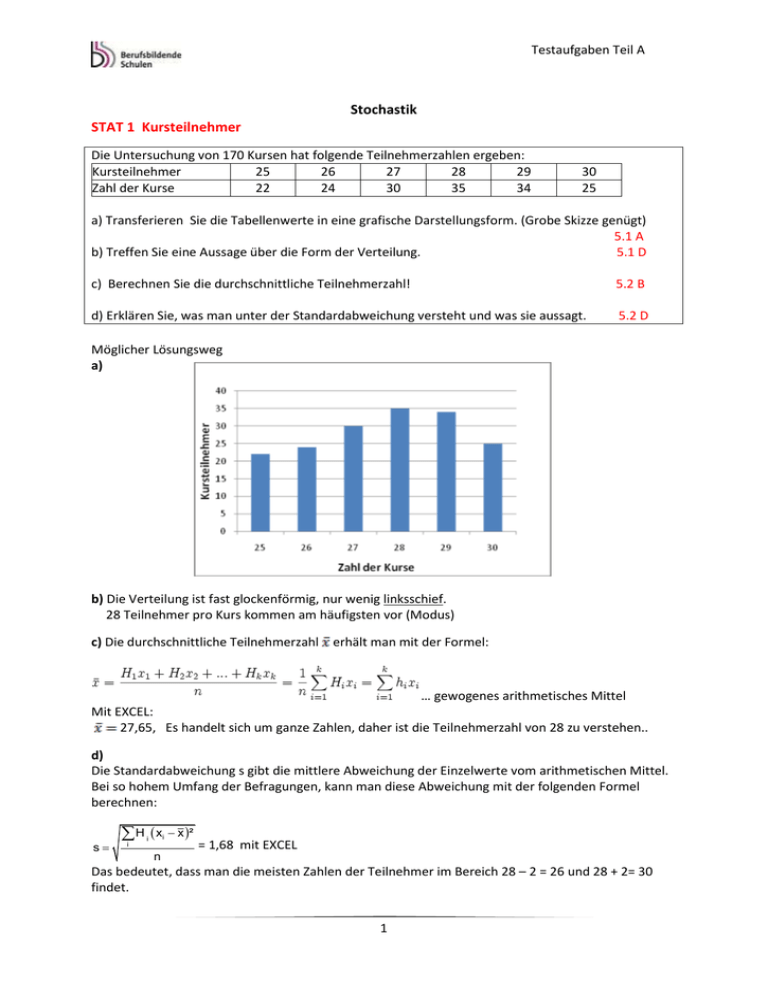
Testaufgaben Teil A
Stochastik
STAT 1 Kursteilnehmer
Die Untersuchung von 170 Kursen hat folgende Teilnehmerzahlen ergeben:
Kursteilnehmer
25
26
27
28
29
Zahl der Kurse
22
24
30
35
34
30
25
a) Transferieren Sie die Tabellenwerte in eine grafische Darstellungsform. (Grobe Skizze genügt)
5.1 A
b) Treffen Sie eine Aussage über die Form der Verteilung.
5.1 D
c) Berechnen Sie die durchschnittliche Teilnehmerzahl!
5.2 B
d) Erklären Sie, was man unter der Standardabweichung versteht und was sie aussagt.
5.2 D
Möglicher Lösungsweg
a)
b) Die Verteilung ist fast glockenförmig, nur wenig linksschief.
28 Teilnehmer pro Kurs kommen am häufigsten vor (Modus)
c) Die durchschnittliche Teilnehmerzahl erhält man mit der Formel:
… gewogenes arithmetisches Mittel
Mit EXCEL:
27,65, Es handelt sich um ganze Zahlen, daher ist die Teilnehmerzahl von 28 zu verstehen..
d)
Die Standardabweichung s gibt die mittlere Abweichung der Einzelwerte vom arithmetischen Mittel.
Bei so hohem Umfang der Befragungen, kann man diese Abweichung mit der folgenden Formel
berechnen:
s
H  x
i
i
n
i
 x ²
= 1,68 mit EXCEL
Das bedeutet, dass man die meisten Zahlen der Teilnehmer im Bereich 28 – 2 = 26 und 28 + 2= 30
findet.
1
Testaufgaben Teil A
STAT 2 Körpermasse
Ein Schularzt protokolliert die Körpermassen der Schüler eines Jahrgangs und erhält dabei die
folgende Aufstellung hinsichtlich (Masse in kg/Häufigkeit):
(60/2), (61/3), (62/7), (63/11), (64/21), (65/21), (66/12), (67/15), (68/5), (69/3), (70/1), (71/1).
a. Transferieren Sie die gegebenen Wertepaare in eine grafische Darstellungsform.
b. Treffen Sie eine Aussage über die Form der Verteilung.
c. Berechnen Sie das durchschnittliche Gewicht der Schüler.
d. Begründen Sie, warum der Median aussagekräftiger ist als das arithmetische Mittel.
e. Die Standardabweichung dieser Daten beträgt 2,1. Interpretieren Sie diesen Wert.
5.1 A
5.1D
5.2B
5.2D
5.2C
Möglicher Lösungsweg:
a.
KG
60
61
Häufigkeit 2
3
70
1
62
7
63
11
64
21
65
21
66
12
67
15
68
5
69
3
71
1
Anzahl der Schüler
25
20
15
10
5
0
60
61
62
63
64
65
66
67
68
69
70
71
Körpermasse in kg
b. Annähernd Normalverteilung (Glockenkurve), fast symmetrisch – Unregelmäßigkeit bei 67 kg. Das
häufigste Gewicht der Schüler liegt bei 64 und 65 kg.
c. Gewogenes arithmetisches Mittel x = 65 kg (EXCEL)
d. Median = 65,5kg, teilt Liste in 2 Teile und berücksichtigt keine Ausreißer
e. Die Standardabweichung beschreibt die mittlere Abweichung der einzelnen Körpermassen vom
Mittelwert. Sie berechnet man bei großem n durch die Formel
s
H  x
i
i
 x ²
i
n
Im Falle der Aufgabenstellung bedeutet es, dass es eine mittlere Abweichung vom Mittelwert um 2
kg nach oben und nach unten gibt.
2
Testaufgaben Teil A
STAT 3 Studienabschlüsse
Die Tabelle bezieht sich auf die Studienabschlüsse an Österreichs Universitäten:
Anzahl Summe
2000 - 2005
45 213
m
 18,9%
 18,3%
 20,0%
 21,8%
 21,1%
49 077
w
 17,6%
 17,5%
 20,0%
 21,6%
 23,3%
94 290
Gesamt  18,2%
 17,9%
 20,0%
 21,7%
 22,2%
a) Rechnen Sie die prozentuellen Häufigkeiten (m/w/ gesamt) in absolute Häufigkeiten um. 5.1 B
2000/01
2001/02
2002/03
2003/04
2004/05
b) Interpretieren Sie die Prozentangaben der männlichen und weiblichen Absolventen der
Unis und vergleichen Sie sie in einem Stabdiagramm.
5.1 C
c)
„Die Daten beweisen eine Zunahme der Akademikerquote in Österreich.“ Nehmen Sie zu
dieser Aussage unter Berücksichtigung der vorliegenden Daten Stellung und bringen Sie
Argumente für Ihre Auffassung.
5.1D
Möglicher Lösungsweg
a)
Anzahl
m
w
ges
00/01
8545
8638
17161
01/02
8274
8588
16878
02/03
9043
9815
18858
03/04
9856
10601
20461
04/05
9540
11435
20932
b)
c) Aufgrund der wachsenden Zahlen in der Tabelle kann auf dem ersten Blick von einer
Zunahme gesprochen werden.
Eine genauere Betrachtung verlangt allerdings die Berücksichtigung zB des
Bevölkerungswachstums in Österreich, die der "Quote" zugrunde liegt. Auch die Anzahl
jener zwischen 2000 und 2005 ausgewanderter oder verstorbener Akademiker sind in der
Tabelle zwar als Studienabschließende berücksichtigt, tragen aber zu den Akademikern im
Land nicht bei.
3
Testaufgaben Teil A
STAT 4 Bioeier
Eine Auswahl von 36 Bio-Eiern wurde gewogen. Die Messwerte in Gramm sind:
57
62
59
54
57
61
54
63
62
60
57
54
56
58
63
64
72
59
60
62
57
58
57
62
59
54
57
61
54
63
62
60
57
a) Erstellen Sie eine Strichliste für die ausgewählten Bio-Eier.
55
59
55
5.1 A
b) Interpretieren Sie die nachstehende Häufigkeitsverteilung und stellen Sie die in einem
Stabdiagramm dar.
5.1 C
c) Berechnen Sie das arithmetische Mittel der Massen der 36 Bio-Eier.
5.2 B
d) Interpretieren Sie die Häufigkeitsverteilung, indem Sie den Modus ablesen und den
Unterschied zum arithmetischen Mittel von 59 g angeben.
5.2 C
e) Erklären Sie, wann man als Zentralwert den Modus dem arithmetischem Mittelwert
vorzieht.
5.2 D
Lösungsvorschlag
a) Strichliste für die ausgewählten Bio-Eier.
54 ||||
55 ||
56 |
57 |||| ||
58 ||
4
Testaufgaben Teil A
59 ||||
60 |||
61 ||
62 ||||
63 |||
64 |
72 |
b) Häufigkeitsverteilung in einem Stabdiagramm
c) Das arithmetische Mittel der Massen der 36 Bio-Eier.
x
1
2124
 (5  54  2  55  ...  72) 
 59
36
36
Das arithmetische Mittel der Eiermassen ist 59 g.
d) Lesen Sie aus der Häufigkeitsverteilung den Modus ab und geben Sie den absoluten und relativen
Unterschied zwischen diesem und dem arithmetischen Mittel von 59 g an.
Der häufigste Wert, der Modus, ist 57 g mit einer absoluten Häufigkeit von 7.
Der absolute Unterschied zum arithmetischen Mittel ist –2 g.
e) Das eine Ausreißer-Ei mit 72 g führt dazu, dass das arithmetische Mittel über dem Modus liegt.
Wenn es Ausreißer in der Verteilung gibt, dann eignet sich der Modus zur Beschreibung des
Zentralwerts besser als das durch den Ausreißer stark veränderte arithmetische Mittel.
5
Testaufgaben Teil A
STAT 5 Bruttolohn
In einem Betrieb wurde eine Erhebung über den Bruttolohn der Angestellten gemacht, es
wurden 280 Personen befragt. Das Ergebnis mit 1GE = 1000 Euro
Mittlerer Gehalt GE 1,0 1,4 1,8 2,2 2,6 3,0 3,4 3,8
Anzahl
30
68
72
51
22
3
24
10
Die Klasseneinteilung in den Gehaltsstufen wurde geändert, dadurch trat eine Verschiebung in der
Häufigkeitsverteilung ein:
Mittlerer Gehalt GE 1,0 1,5 2,0 2,5 3,0 3,5 4,0
Anzahl
67
93
61
29
25
8
4
a) Transferieren Sie beide Datensätze in jeweils ein Diagramm zur Häufigkeitsverteilung.
b) Treffen Sie eine Aussage über die augenscheinlich sehr unterschiedlichen Daten, obwohl
gleich großer Datenumfang die Grundlage bildet.
c) Berechnen Sie das gewichtete arithmetische Mittel der Gehälter in der ersten Tabelle.
d) Erklären Sie, was man unter Standardabweichung versteht und was sie angibt.
5.1 A
ein
5.1 D
5.2 B
5.2 D
Lösungsvorschlag:
a) Verteilung der Gehälter
b) Die Personen befinden sich in der
ersten Tabelle mit ihren Gehältern eher
am unteren Rand der Gehaltsklasse,
deshalb rutschen bei der zweiten
Klasseneinteilung viele in die darunter
liegende Gehaltsklasse ab.
c) Das gewichtete arithmetische Mittel
der Gehälter liegt nach der ersten Tabelle
bei € 1.974,29.
Anzahl der Personen
100
90
80
70
60
d) Die Standardabweichung ist ein Maß
für die mittlere Abweichung vom
Anzahl der Personen
arithmetischen Mittelwert im Verhältnis
zu seiner Größe. Sie liefert eine Aussage
darüber, ob die vorhandene Datenmenge
eher homogen oder inhomogen ist.
50
40
30
20
10
0
1
2
3
4
5
6
7
6
Testaufgaben Teil A
STAT6 Intelligenzquotient
Der Intelligenzquotient von 614 zufällig ausgewählten Personen wurde ermittelt.
Die gerundeten Werte verteilen sich wie folgt:
a) Transferieren Sie die Tabellenwerte in eine grafische Darstellung.
5.1 A
b) Treffen Sie eine Aussage über die Form der Verteilung.
5.1D
c) Berechnen Sie den durchschnittlichen IQ der ausgewählten Personen.
5.2 B
d) Erklären Sie, was man unter der Standardabweichung versteht und was sie aussagt. 5.2D
Mögliche Lösung:
a)
b) Die Verteilung beinahe glockenförmig.
c) Den durchschnittlichen IQ erhält man mit der Formel:
x=
H1x1 +H2x2 +...+Hk xk
n
(gewogenes arithmetisches Mittel). Mit Excel: x =100,41
d)
Die Standardabweichung s gibt die mittlere Abweichung der Einzelwerte vom arithmetischen Mittel
an. Man kann die Standardabweichung mit folgender Formel berechnen:
s=
åH ( x - x )
i
2
i
i
n
Für dieses Beispiel gilt: s = 18,32 (mit EXCEL)
Das bedeutet, dass der IQ der meisten Personen im Bereich 100 – 18 = 82 und 100 + 18 = 118 liegt.
7
Testaufgaben Teil A
BIN 1 Würfelspiel
Beim Spielen mit einem Würfel stellt ein Spieler fest, dass die Augenzahl „1“ überdurchschnittlich
häufig, die Augenzahl „6“ dagegen relativ selten auftritt.
Dies führt zu der Vermutung, dass die Wahrscheinlichkeit für das Würfeln einer „6“ nur 10 %,
einer „1“aber 20 % beträgt und die anderen Augenzahlen mit untereinander gleichen
Wahrscheinlichkeiten auftreten.
Gehen Sie davon aus, dass diese Vermutung zutrifft.
a) Modellieren Sie eine grafische Darstellung für die Wahrscheinlichkeitsverteilung.
5.3 A
b) Berechnen Sie Erwartungswert und Standardabweichung der Zufallsgröße X
5.2 B
(X= Die Augenzahl beim Werfen des Würfels.)
c) Überlegen Sie, wie Sie die Wahrscheinlichkeit berechnen können, dass erst im fünften Wurf zum
ersten Mal eine Sechs auftritt. Erklären Sie Ihre Modellerstellung.
5.5 A
d) Berechnen Sie unter Zuhilfenahme der Binomialverteilung die Wahrscheinlichkeit, dass in 5
Würfen mindestens 2-mal Sechs auftritt.
5.6 B
Eine mögliche Lösung der Testaufgabe
a)
b) E(x) = 0,2 + ( 2+ 3+ 3+ 5)  0,175 + 0,6 = 3,25
Varianz V (x) = 0,2  (-2,25)² + 0,175  ((-1,25)² + (-0,25)² + 0,75² +1,75²) + 0,1  2,75² = 2,6875
σ = ca. 1,64
c) Die Anzahl der Würfe, bis zum ersten Mal die Augenzahl 6 erscheint. Man kann sich dies zB in
einem Baumdiagramm vorstellen. Das Diagramm hat – gemäß eines Bernoulli-Zufalls-Experiments
die Äste Sechs und nicht Sechs. Sechs hat 10% Wahrscheinlichkeit, nicht Sechs daher 90%. Nun
sind 4 Würfe ohne Sechs bereits verlaufen. Beim 5. Wurf kommt das 1. Mal Sechs. Es gibt nur
einen Ast im Diagramm, der diese Bedingung erfüllt. Laut Pfadregel berechnet man die
Wahrscheinlichkeit daher P(X) = 0,94  0,1 = 0,0656.
d) P(mi 2-mal) = 1- P(0) - P(1) = 1- 0,95 - 5  0,940,1 = 0,081 = 8,1 % wahrscheinlich.
8
Testaufgaben Teil A
BIN 2 Aufnahmetest
Ein Aufnahmetest enthält 25 Fragen, wobei von jeweils vier vorgegebenen Antworten genau eine
richtig ist. Eine Testperson kreuzt die Antworten rein zufällig an.
a) Erklären Sie, warum die Wahrscheinlichkeit, dass eine einzelne Testaufgabe richtig gelöst wird,
25% beträgt.
5.3 D
b) Berechnen Sie, wie viele richtige Antworten die Testperson erwarten kann?
5.4 B
c) Berechnen Sie die Wahrscheinlichkeit, dass die Person den Test besteht, wenn dazu mindestens
14 richtige Antworten nötig sind?
5.6B
d) Die Ersteller des Tests möchten die Wahrscheinlichkeit für das Bestehen des Tests durch zufälliges
Ankreuzen auf maximal 0,1% reduzieren. Beschreiben Sie, durch welche Maßnahme man dies
erreichen kann?
5,6 C
Lösung:
a) Von 4 möglichen Antworten ist 1 richtig. Wahrscheinlichkeit = günstige Fälle / mögliche Fälle  ¼
b) Erwartungswert = 25  0,25 = 6,25  maximal 6 richtige Antworten
c) P(X >=13) = 1 - P(X <= 12) = binomvert(12;25;0,25;1) = 0,34%
d) Durch Erhöhen der Aufgabenzahl
Alternative: Durch Erhöhen der Anzahl der jeweils vorgegebenen Antworten.
9