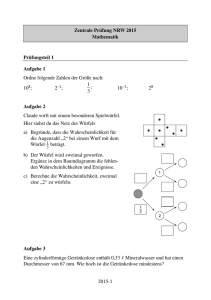
2004_2 - Stochastik in der Schule

Stochastik in der Schule
SiS
Zeitschrift des Vereins zur Förderung des schulischen Stochastikunterichts
Inhaltsverzeichnis
Heft 2, Band 24 (2004)
GERD GIGERENZER
Die Evolution des statistischen Denkens
2
HELMUT WIRTHS
Wie gut kannst Du schätzen?
Und andere Probleme für den Statistik-Unterricht
14
JÖRG MEYER
Vernetzungen zwischen Vektorgeometrie
und beschreibender Statistik
24
GERHARD KÖNIG
Gerd Gigerenzer: Das Einmaleins der Skepsis
Rezension
30
GERHARD KÖNIG
Bibliographische Rundschau
32
Vorwort der Herausgeberin
Besonders faszinierend an der Geschichte der Stochastik ist, dass sie ihren Anfang in der etwas verrufenen
Welt des Glückspiels nahm, um sich dann allmählich dank der Mathematiker der Aufklärung als respektable
Wissenschaft zu etablieren. Gerd Gigerenzers Beitrag ist eine spannende Kurzgeschichte der Stochastik. Er
erläutert die wesentlichen Inhalte anschaulich und leicht verständlich – es genügen Grundkenntnisse der
Bruchrechnung – vor dem Hintergrund ihrer historischen Entstehung. Dabei eröffnen sich verblüffende
Einblicke in die Zusammenhänge zwischen aktuellen statistischen Methoden und ihren soziokulturellen
Wurzeln. Die geschichtliche Repräsentation – so Gigerenzer – unterstützt stets das Verständnis von
Resultaten und Methodologien. Der Artikel von Helmut Wirths bietet eine enthusiastische Ermunterung,
Schüler/innen mit dem Umgang von Daten vertraut zu machen. Der Autor beschreibt ein neuartiges Projekt,
bei dem Schüler/innen selbstständig Daten zu ihnen bekannten, alltäglichen Bereichen erheben, dazu
selbstständig Fragestellungen entwickeln und diese dann auch noch selbstständig beantworten. Im dritten
Artikel verfolgt Jörg Meyer einen interdisziplinären Zugang zu den Hauptbegriffen der Statistik. Elegant
und verständlich stellt er die „natürliche“ Brücke zwischen Statistik und Vektorgeometrie dar. Die
Hauptelemente der Statistik werden umfassend und konsequent als vektorgeometrische Konstrukte
präsentiert.
„Das Einmaleins der Skepsis“ von Gerd Gigerenzer ist Gegenstand der Buchrezension. Das interessante
Werk, das eher für das allgemeine Publikum geschrieben ist, bietet auch für Stockastiklehrer/innen eine
Fundgrube an lehrreichen Beispielen. Die bibliographische Rundschau von Gerhard König ist wie immer
reich an guten Hinweisen zur aktuellen Literatur.
Das vorliegende Heft sei den Leser(inne)n auch eine spannende Begleitung in der Ferienzeit!
Laura Martignon
Die Evolution des statistischen Denkens
Wiederabdruck aus: Unterrichtswissenschaft – Zeitschrift für Lernforschung,
32. Jahrgang , 2004, Heft 1, S. 4 – 22. Wir danken dem Verlag für die
freundliche Genehmigung.
GERD GIGERENZER
Lernen mit Unsicherheit zu leben – statistisches
Denken – ist der wichtigste Teil der Mathematik im
wirklichen Leben. Denken ist das Hinterfragen von
Gewissheiten, und man lernt es anhand von guten
Beispielen. Zu den besten gehören jene Probleme,
welche die Entwicklung des statistischen Denkens
tatsächlich geprägt haben. Genau dies ist das
Programm meines Artikels.
Der Beginn der mathematischen Theorie der
Wahrscheinlichkeit wird auf 1654 datiert. Anders
als die meisten großen Ideen, die bereits in der
griechischen Antike entwickelt worden sind, ist das
Konzept der mathematischen Wahrscheinlichkeit
eine ungewöhnlich späte Entdeckung. Der
Philosoph Ian Hacking hat dies als den „Skandal
der Philosophie“ bezeichnet. Die Geschichte der
Wahrscheinlichkeit ist also relativ kurz, und sie ist
bestens dokumentiert (z.B. Daston, 1988;
Gigerenzer et al., 1999; Hacking, 1975, 1990). Ich
werde diese Entwicklung hier nicht nacherzählen,
sondern einen anderen Weg gehen: eine kurze Geschichte in Form klassischer Denkprobleme und
der Bedeutung des statistischen Denkens als dem
Einmaleins des skeptischen Denkens, damals und
heute. Ich beginne mit einem fanatischen Spieler
und zwei großen Mathematikern.
1. Die Wette des Chevalier
Der Chevalier de Méré war ein leidenschaftlicher
Spieler und lebte im Frankreich des 17.
Jahrhunderts. Eines der Spiele, mit denen er seine
Mitspieler verführte, war das folgende: „Wir
werfen einen Würfel viermal. Wenn dabei eine
oder mehrere Sechsen sind, gewinne ich. Wenn
keine Sechs dabei ist, gewinnen Sie.“ Soweit wir
wissen, waren seine Würfel fair; dennoch gewann
der Chevalier mit diesem Spiel regelmäßig Geld.
Schließlich fand er keine Opfer mehr, oder das
Spiel wurde auf die Dauer eintönig - was immer der
Grund war, er dachte sich eine Variante aus, die
ebenso lukrativ sein sollte. Hier ist das neue Spiel,
das der Chevalier seinen Mitspielern anbot:
Stochastik in der Schule 24 (2004) Heft 2, S. 2 – 13
Doppel-Sechs: Wir werfen ein Paar von
Würfeln 24 Mal. Wenn dabei eine DoppelSechs oder mehrere sind, gewinne ich. Wenn
keine Doppel-Sechs dabei ist, gewinnen Sie.
Würden Sie das Angebot annehmen? De Mérés
Intuition ist durchsichtig. Er wusste aus Erfahrung,
dass es von Vorteil ist, darauf zu wetten, dass
mindestens eine Sechs in einer Serie von 4 Würfen
auftritt. Eine Doppel-Sechs ist aber 6-mal so selten
wie eine einfache Sechs. Daraus schloss er, dass es
von Vorteil ist, darauf zu wetten, dass er
mindestens eine Doppel-Sechs in 24 (also 6 mal 4)
Würfen erhält. Fortuna jedoch enttäuschte den
Chevalier; er begann zu verlieren. War er glücklos,
obgleich er richtig dachte, oder war er glücklos,
weil er falsch dachte? Der Chevalier konnte diese
Frage nicht entscheiden, seine Intuition sprach für
Ersteres, seine Erfahrung für Letzteres.
De Méré wandte sich an die berühmten
Mathematiker Blaise Pascal und Pierre Fermat, die
im Jahre 1654 eine Reihe von Briefen über dieses
und ähnliche Probleme austauschten und einen
allgemeinen Lösungsweg entwickelten. Deshalb
wird 1654 als das Geburtsjahr der mathematischen
Theorie der Wahrscheinlichkeit angenommen. Die
Enttäuschung des Chevalier de Méré war der
Anlass für eine der größten intellektuellen
Revolutionen. Hier ist die Analyse von Pascal und
Fermat, in moderner Terminologie.
Beginnen wir mit dem ersten Spiel. Wie hoch ist
die Wahrscheinlichkeit von mindestens einer Sechs
in einer Serie von vier Würfen? Die
Wahrscheinlichkeit p(Sechs) von einer Sechs in
1
einem Wurf eines fairen Würfels ist . Daher ist
6
die Wahrscheinlichkeit von „keine Sechs“
5
.
6
Die Wahrscheinlichkeit von „keine Sechs“ in einer
Serie von 4 Würfen ist daher:
p(keine Sechs) =
2
p(keine Sechs in 4 Würfen)
5 5 5 5
          .482
6 6 6 6
Also ist die Wahrscheinlichkeit
p(mindestens eine Sechs in 4 Würfen) = .518.
Wir verstehen nun, warum de Méré mit dem ersten
Spiel Geld verdiente. Seine Chance zu gewinnen,
war etwas höher als 50%. Die gleiche Logik lässt
sich auf das Doppel-Sechs Spiel anwenden. Wenn
Sie die Antwort noch nicht sehen, geben Sie nicht
auf. Wir lösen jetzt ein Problem, das vor 1654 noch
niemand gelöst hat. Nochmals, die Frage ist: Wie
hoch ist die Wahrscheinlichkeit, mindestens eine
Doppel-Sechs in 24 Würfen zu erhalten? Die
Wahrscheinlichkeit p(Doppel-Sechs) in einem
1
Wurf mit einem Paar von Würfeln ist
. Daher
36
ist die Wahrscheinlichkeit von „Keiner DoppelSechs“
p(keine Doppel-Sechs) =
35
.
36
Die Wahrscheinlichkeit von „keine Doppel-Sechs“
in einer Serie von 24 Würfen ist daher:
p(keine Doppel-Sechs in 24 Würfen)
 35 
 
 36 
24
 .509 .
Also ist die Wahrscheinlichkeit dafür, mindestens
eine Doppel-Sechs in 24 Würfen zu erhalten gleich
.491. Jetzt sehen wir, dass die Chance, das DoppelSechs-Spiel zu gewinnen, tatsächlich leicht unter
50% liegt. Der Grund warum de Méré verlor, war
also nicht ein Mangel an Glück, sondern eine
falsche Intuition. Doch die Genauigkeit seiner
Erfahrung am Spieltisch ist faszinierend. Er muss
reichlich Mitspieler gefunden und lange Zeit mit
diesem Spiel verbracht haben, um den kleinen
Unterschied zu 50% bemerken zu können. Dieser
Widerspruch zwischen genauer Erfahrung und
falscher Intuition inspirierte Pascal und Fermat, die
Gesetze der Wahrscheinlichkeit zu suchen und zu
finden. Hier sind sie, in moderner Terminologie:
1. Die Wahrscheinlichkeit eines unmöglichen
Ereignisses ist 0 und jene eines sicheren
Ereignisses ist 1.
2. Die Summe der Wahrscheinlichkeiten aller
möglichen Ereignisse ist 1.
3. Wenn A und B unabhängige Ereignisse sind,
dann ist die Wahrscheinlichkeit p(A&B) dafür,
dass A und B eintreten, gleich dem Produkt der
individuellen Wahrscheinlichkeiten:
p(A&B) = p(A)p(B).
Zum Beispiel: Die Wahrscheinlichkeit, eine „7“
mit einem regulären Würfel zu erhalten ist 0 und
jene, eine Zahl zwischen 1 und 6 zu erhalten, ist 1.
Die Summe aller Wahrscheinlichkeiten für die
Ergebnisse 1 bis 6 beträgt 1, und die
Wahrscheinlichkeit, eine „6“ im ersten Wurf und
eine „1“ im zweiten zu erhalten, also von zwei
1
1
unabhängigen Ereignissen, beträgt
mal , das
6
6
1
ergibt
.
36
2. Pascals Wette
Die Gesetze der Wahrscheinlichkeit waren eine
Antwort auf Erfahrungen mit Glücksspielen, aber
dies war nur eine von mehreren Wurzeln. Die
Entwicklung des Denkens in Wahrscheinlichkeiten
war vielmehr Teil einer großen intellektuellen
Revolution: die Aufgabe des Ideals des sicheren
Wissens und die Entwicklung von Formen des
rationalen Umgangs mit einer unsicheren Welt.
Aristoteles teilte unsere Welt einst in zwei Reiche
auf: in die himmlische Welt der unveränderlichen
Ordnungen und des gesicherten Wissens und die
ungeordnete Welt voller Veränderungen und
Ungewissheiten.
Jahrhundertelang
glaubten
Mathematiker wie auch Theologen und ihre
gläubigen Anhänger, sie lebten in einer Welt
absoluter Gewissheit. Doch die Reformation und
die Gegenreformation unterhöhlten weitgehend das
Reich der Gewissheit. Allmählich setzte sich ein
bescheideneres Ideal durch. Man fand sich damit
ab, dass vollständige Gewissheit des Wissens
unerreichbar ist, hielt aber trotzdem daran fest, dass
das verfügbare Maß an Wissen ausreicht, um
vernünftige Menschen in Theorie und Praxis zu
lenken.
Religiöse Überzeugungen waren und sind noch
heute von emotionaler Gewissheit gefärbt, und das
gilt für Gläubige wie auch für Atheisten. Man weiß
mit absoluter Sicherheit, dass Gott existiert. Oder
es erscheint unbezweifelbar, dass er nicht existiert.
In seinen Pensées aber stellt Blaise Pascal (1669,
Bd. 2, S. 141-55) die religiöse Frage in einem
völlig anderen Licht. Es geht nicht mehr um die
Wahrheit, sondern um die Erwartung. Eine
Erwartung ist nicht sicher, sondern wie eine Wette.
Pascals Wette kann man so zusammenfassen:
Pascals Wette: Ich weiß nicht, ob Gott existiert.
Aber ich weiß, wenn ich an ihn glaube und er
3
nicht existiert, dann werde ich einige Momente
weltlicher Lust und Laster versäumen. Wenn
ich aber nicht an ihn glaube und er dennoch
existiert, dann werde ich mit ewiger
Verdammung und ewigem Elend dafür
bezahlen. Wor-auf soll ich wetten?
Für Pascal ist die Antwort klar: Auch wenn man
die Chance, dass Gott existiert, für beliebig gering
hält, werden doch, falls er existiert, die Folgen
unabsehbar hoch sein: unendlich die Seligkeit der
Erlösten, aber auch unendlich das Elend der
Verdammten. Unter diesen Umständen, so Pascals
Argument, verlangt rationales Eigeninteresse, dass
wir unsere sicheren, aber nur endlichen weltlichen
Freuden dem ungewissen, aber unendlichen
Gewinn der Erlösung opfern.
Pascals Wette illustriert eine radikal neue
Denkweise, die mit der Entwicklung der
Wahrscheinlichkeitstheorie einhergeht. Religiosität
ist eine Frage der Erwartung, nicht des unbedingten
Glaubens, und diese Erwartung ist unsicher. Es ist
wohl kein Zufall, dass zur selben Zeit, als das neue
Denken in Wahrscheinlichkeiten und Erwartungen
Fuß fasste, der Gebrauch der Folter in Europa
zurückging. In der Inquisition war die Folter das
Werkzeug,
um die
eindeutige
Wahrheit
herauszufinden - ein Zweck, der die Mittel heiligte.
Pascals
Grundbegriff
war
nicht
die
Wahrscheinlichkeit, sondern die Erwartung, die
später als Produkt aus der Wahrscheinlichkeit pi
eines Ereignisses i und seinem Wert xi bestimmt
wurde:
E = ∑pixi.
Beispielsweise beträgt am Rouletttisch die
Wahrscheinlichkeit von „Rot“ und „Schwarz“
jeweils 18/37 und jene von „Grün“ (null) beträgt
1/37. Wenn man 100 € auf „Rot“ setzt, beträgt also
die Erwartung
18
 200 
18
0€ 
1
 0 €  97.79 €
37
37
37
Die Definition von rationalem Verhalten durch die
Erwartung wurde zum Grundstein des neuen
Verständnisses
dafür,
mit
Unsicherheiten
umzugehen, statt sie zu verleugnen, und mit
falschen Sicherheiten zu leben. Aber die Definition
von rationalem Handeln als Maximierung der
Erwartung war noch nicht das Ende der
Geschichte. Die mathematische Erwartung geriet
bald in unerwartete Schwierigkeiten.
3. Das St.-Petersburg-Paradox
Das St.-Petersburg-Paradox brachte den ersten
großen Konflikt zwischen dem Konzept der
rationalen Erwartung und dem gesunden
Menschenverstand (Jorland, 1987). Nicholas
Bernoulli wies als Erster in einem Brief an Pierre
de Montmort auf das Problem hin; dieser
veröffentlichte es in der zweiten Auflage seines
Essai d’ analyse sur les jeux de hasard (1713).
Daniel Bernoulli, ein Vetter von Nicholas,
veröffentlichte im Jahre 1738 eine mögliche
Lösung in den Jahrbüchern der Petersburger
Akademie, daher kommt der Name des Problems.
St.-Petersburg-Spiel: Pierre und Paul spielen
ein Glücksspiel mit einer fairen Münze. Wenn
das Ergebnis des ersten Wurfs „Zahl“ ist, muss
Pierre an Paul 1 € zahlen und das Spiel ist
beendet. Wenn „Zahl“ erst beim zweiten Wurf
kommt, erhält Paul 2 €; wenn dies erst beim
dritten Wurf geschieht, gewinnt er 4 € und so
weiter. Wie hoch ist der faire Preis, den Paul
zahlen sollte, um das Spiel zu spielen?
Wie viel würden Sie bieten? Der faire Preis ist jene
Summe, bei der eine Person unentschieden ist, die
Rolle von Pierre oder die von Paul zu spielen.
(Wenn ein Kind ein Stück Kuchen in zwei Teile
teilt, und das andere Kind die Wahl hat, handelt es
sich um dasselbe Prinzip von Fairness.) Nach der
klassischen Theorie der Rationalität ist der faire
Preis durch die mathematische Erwartung definiert:
1
 1
 1

E   1 €     2 €     4 € 
2
4
8

 
 

 1  n

 ...     2 n 1 €   ...  
 2 

In Worten, mit der Wahrscheinlichkeit p =
gewinnt Paul 1 €, mit p =
1
2
1
gewinnt er 2 €, mit
4
1
gewinnt er 4 € und so weiter. Man kann
8
sehen, dass jedes der Glieder auf der rechten Seite
1
der Gleichung einer Erwartung von
€ entspricht,
2
und da deren Anzahl unendlich ist, ist der
Erwartungswert ebenfalls unendlich groß. Gemäß
der Theorie, dass die Erwartung der faire Preis ist,
sollte jeder von uns all sein Vermögen einsetzen,
um dieses Spiel zu spielen - und dies würde sogar
noch von Vorteil sein, da das Vermögen ja nur
endlich groß ist. Kein vernünftiger Mensch ist
p=
4
jedoch bereit, mehr als eine kleine Summe,
vielleicht 5 bis 10 €, für dieses Spiel zu bieten.
Die Mathematiker nannten diesen Widerspruch
zwischen
Theorie
und
gesundem
Menschenverstand das „St.-Petersburg-Paradox“.
Nach unserem heutigen Verständnis liegt aber kein
Paradox vor: Es gibt keinen Widerspruch zwischen
Resultaten, die sich aus gleich validen Annahmen
ableiten lassen. Nach dem klassischen Verständnis
war die Theorie der Wahrscheinlichkeit jedoch
keine reine, inhaltsfreie Theorie, sondern
untrennbar von ihrem Gegenstand. Und dieser
Gegenstand war die menschliche Vernunft. Der
Widerspruch zwischen Theorie und Vernunft
wurde daher als ein Paradox interpretiert.
Daniel Bernoulli versuchte diesen Widerspruch zu
lösen. Er argumentierte, dass es beim St.Petersburg-Problem nicht alleine um Fairness gehe
und man anstelle der mathematischen Erwartung
die „moralische“ Erwartung des umsichtig
abwägenden Kaufmanns einführen sollte. Diese
definierte er als das Produkt aus der
Wahrscheinlichkeit des Ergebnisses und dem, was
später sein Nutzen genannt wurde. Bernoulli
argumentierte, dass ein Gewinn von 200 € (in
moderner Währung) nicht notwendigerweise
doppelt soviel wert ist wie ein Gewinn von 100 €,
und dass ein Spieler umso mehr Geld gewinnen
muss, um glücklich zu werden, je reicher er schon
ist. Nehmen wir an, die Beziehung zwischen € (x)
und Nutzen N ist logarithmisch, N(x) = ln(x), und
ihr derzeitiges Vermögen V beträgt 50.000 €. Dann
berechnet sich der sichere Gewinn G, der
denselben Nutzen hat wie die Teilnahme am St.Petersburg-Spiel, wie folgt:
1
1
1
N (V 1)  N (V  2)  N (V  4)  ...
2
4
8
Die Berechnung ergibt einen Wert von etwa 9 €. In
Worten ausgedrückt, für jemanden, der ein
Vermögen von 50.000 € besitzt, beträgt der
erwartete Nutzen dieses Spiels nur 9 €. Dieser Wert
liegt im Bereich dessen, was jemand mit einem
gesunden Menschenverstand bereit ist, für das
Spiel zu zahlen.
Mit dieser Lösung des St.-Petersburg-Paradox
transformierte Daniel Bernoulli das Konzept des
erwarteten Werts von Pascal-Fermat in das
Konzept des erwarteten Nutzens, das auch heute
noch die Wirtschaftswissenschaften dominiert.
Nicholas Bernoulli, der Professor für Römisches
und Kanonisches Recht an der Universität Basel
war, hielt dagegen weiterhin an Fairness als Modell
der menschlichen Vernunft fest, da er dieses als die
N (V G) 
Grundlage für rechtliche Verträge ansah. Daniel
Bernoulli nahm dagegen seine Inspiration aus der
Welt von Handel und Gewerbe, nicht aus dem
Recht. Für ihn war Vernünftigkeit kluger
Geschäftssinn, und es war sicherlich nicht
wirtschaftlich klug, eine hohe Summe in das St.Petersburg-Spiel zu investieren. Für sein neues
Verständnis von rationalem Verhalten war der
Prototyp eines vernünftigen Menschen nicht mehr
der unparteiische Richter, sondern der umsichtig
abwägende Kaufmann. Die mathematische Theorie
der menschlichen Vernunft hatte eine Wende
vollzogen.
4. Pro Monogamie: Der erste
Nullhypothesentest
Die mathematische Wahrscheinlichkeit hat drei
Quellen: Glücksspiel, Gerichtshof und statistische
Tabellen. Die drei Hauptinterpretationen des
Konzepts der Wahrscheinlichkeit entstammen
diesen drei Anwendungen: Propensität, subjektive
Wahrscheinlichkeit
und
Häufigkeit.
Mit
Propensität (Englisch: propensity) ist das Design
eines Würfels oder eines Roulettrads gemeint, das
die Wahrscheinlichkeit bestimmt. Das Konzept der
subjektiven Wahrscheinlichkeit kommt aus
rechtlichen Fragen, etwa wie hoch ein Richter die
Glaubwürdigkeit von Zeugen einschätzen soll, zum
Beispiel wenn diese mit dem Angeklagten
verwandt oder nicht verwandt sind. Die
Interpretation von Wahrscheinlichkeit als relative
Häufigkeit auf lange Sicht basiert auf statistischen
Informationen
wie
Geburtenund
Sterblichkeitstabellen. Diese Tabellen waren eine
der ersten systematischen Datenbanken, die in der
westlichen Welt angelegt wurden, und zugleich die
Basis für den ersten Nullhypothesentest.
John Arbuthnot (1710) stellte eine alte Frage: Gibt
es einen aktiven Gott? Seine Methode, eine
Antwort zu finden, aber war neu und revolutionär.
Er suchte nach Fakten statt Rhetorik und nach
einem empirischen Test. Arbuthnot beobachtete,
dass Männer gefährlicher leben als Frauen und dass
mehr junge Männer als Frauen durch Unfälle
sterben. Wenn es einen aktiven Gott gibt und dieser
Monogamie vorsieht, so argumentierte er, wird er
mehr Jungen als Mädchen erzeugen, um diesen
Verlust zu kompensieren. Arbuthnot testete diese
Hypothese göttlicher Vorsehung gegen die
Nullhypothese von blindem Zufall. Dazu
untersuchte er die Geburtenstatistiken, die damals
seit 82 Jahren in London geführt wurden. Er stellte
fest, dass in jedem der 82 Jahre mehr Jungen als
Mädchen geboren wurden, und berechnete die
5
„Erwartung“ dieses Ergebnisses (D) unter der
Nullhypothese (H0):
82
1
p D | H 0     .
2
Weil diese Wahrscheinlichkeit so außerordentlich
klein war, schloss er blinden Zufall aus und sah das
Ergebnis als Beweis für die göttliche Vorsehung.
Hier ist seine Folgerung in seinen eigenen Worten:
„Scholium. From hence it follows, that Polygamy is contrary to the Law of Nature and Justice, and to the Propagation of the human Race;
for where Males and Females are in equal
number, if one Man takes Twenty Wifes, Nineteen Men must live in Celibacy, which is repugnant to the Design of Nature; nor is it probable that Twenty Women will be so well impregnated by one Man as by Twenty.“
Arbuthnots Idee, eine Behauptung gegen
statistische Daten zu testen, war revolutionär und
seiner Zeit weit voraus. Nullhypothesentests kamen
erst im späten 19. Jahrhundert und frühen 20.
Jahrhundert in Gebrauch und wurden durch die
Arbeiten des Statistikers und Genetikers Sir Ronald
Fisher popularisiert. Arbuthnots Test macht
zugleich die Möglichkeiten und Grenzen eines
Nullhypothesentests (Arbuthnot verwandte diesen
Begriff noch nicht) so klar wie kaum ein späteres
Beispiel. Dieser Test liefert die Wahrscheinlichkeit
einer Serie von Beobachtungen (in jedem von 82
Jahren mehr Jungen als Mädchen), falls die
Nullhypothese gilt. Die erste Beschränkung liegt
darin, dass in dieser Methode per Definition die
Forschungshypothese (hier: göttliche Vorsehung)
selbst nicht in statistischer Form formuliert wird.
Die göttliche Vorsehung gewinnt immer, falls die
Nullhypothese verliert, die einzige Bedingung hier
ist, dass mehr Jungen geboren werden. Welches
Verhältnis
aber
die
Forschungshypothese
vorhersagt, wird nicht spezifiziert. Die zweite
Beschränkung
liegt
darin,
dass
keine
Alternativhypothese in statistischer Form getestet
wird.
Beispielsweise
könnte
eine
Alternativhypothese besagen, dass 3% aller
weiblichen Neugeborenen unmittelbar nach der
Geburt illegal ausgesetzt oder getötet werden und
deshalb nicht in der Statistik auftauchen. Selbst
wenn das der Fall ist, würde Arbuthnots Test
dennoch diesen Effekt der göttlichen Vorsehung
zuschreiben. Der Mangel an präzisen Forschungsund Alternativhypothesen ist das größte Problem in
Arbuthnots Test, und das gilt ebenfalls für die
heutigen Anwendungen von Nullhypothesentests in
den Sozialwissenschaften (Gigerenzer, 1993).
Die Bedeutung von Arbuthnots Vorgehen liegt
jedoch nicht in der besonderen Struktur dieses
Nullhypothesentests,
sondern
in
der
bahnbrechenden Idee, Fragen durch Heranziehen
empirischer Daten zu entscheiden. Dies war damals
ein revolutionäres Vorgehen, doch die Revolution
selbst musste noch fast zwei Jahrhunderte warten.
Arbuthnots Test fand keine Beachtung. Wenn wir
uns darüber wundern, sollten wir nicht vergessen,
dass es auch heute keine Ausnahme ist, dass
Ideologien statt empirischer Evidenz über religiöse,
pädagogische und politische Fragen entscheiden.
5. Wer entdeckte die Regel von
Bayes?
Das Testen einer Nullhypothese blieb nicht die
einzige Methode, eine Hypothese zu testen. Die
Regel von Bayes ist eine der bekanntesten
Alternativen. Thomas Bayes (1702-1761) war ein
Reverend der „Nonconformist Church“. Er hat
seine berühmte Abhandlung über das Problem der
„inversen
Wahrscheinlichkeit“
die
Wahrscheinlichkeit einer Hypothese gegeben
Evidenz - nie selbst veröffentlicht. Dafür hat ihm
R. A. Fisher (1935) später gratuliert, denn Fisher
war der Meinung, dass die Regel von Bayes für das
Testen wissenschaftlicher Hypothesen nutzlos sei.
In Fishers Augen hatte Bayes dies erkannt, doch
seine Bewunderer nicht. Die Regel von Bayes
wurde nach seinem Tod von Richard Price im Jahre
1763 publiziert.
Für den einfachsten Fall mit binären Hypothesen,
H1 und H2, und einem Datum (Evidenz) D ergibt
sich die Regel von Bayes (in moderner
Terminologie) als:
p(H 1 | D) =
p(H )p(D | H )
1
1
p(H )p(D | H )  p(H )p(D | H )
1
1
2
2
In Worten ausgedrückt, die Aposteriori-Wahrscheinlichkeit p(H1|D) ergibt sich aus der AprioriWahrscheinlichkeit
p(H1)
und
den
Wahrscheinlichkeiten p(D|H1) und p(D| H2).
Betrachten wir eine moderne Anwendung, HIVScreening für Personen ohne Risikoverhalten, das
heißt, HIV-Tests für Personen, die z.B. nicht
intravenös Drogen spritzen (Gigerenzer, 2002). Mit
einem positiven Testergebnis (D) ist hier gemeint,
dass eine Blutprobe sowohl in dem Suchtest (Elisa)
als auch in dem Bestätigungstest (Western-BlotTest) positiv testet.
In Deutschland ist etwa einer von je 10.000
Männern ohne Risikoverhalten HIV-infiziert. Die
Wahrscheinlichkeit p(D|H1), dass der Test positiv
6
(D) wird, wenn der Mann infiziert ist, beträgt .999.
Die Wahrscheinlichkeit p(D|H2), dass der Test
positiv wird, wenn der Mann nicht infiziert ist,
beträgt .0001. Ein Mann testet positiv. Wie hoch ist
die Wahrscheinlichkeit p(H1|D), dass er wirklich
mit dem Virus infiziert ist?
Wenn man diese Werte in die Regel von Bayes
einsetzt, dann erhält man einen Wert von
p(H1|D) = .5. Nur jeder zweite, der positiv testet,
hat demnach tatsächlich den Virus. Die meisten
professionellen AIDS-Berater an deutschen
Gesundheitsämtern teilen Klienten dagegen
fälschlicherweise mit, dass es absolut sicher oder
zumindest zu 99,9% sicher sei, dass man infiziert
sei (Gigerenzer, Hoffrage & Ebert, 1998). Die
Ausbildung dieser Berater im statistischen Denken
lässt sehr zu wünschen übrig. Die Folgen dieser
Fehlinformation können vom Verlust des
Arbeitsplatzes bis zum Selbstmord reichen.
Die Regel von Bayes ist vom Testen von
Nullhypothesen zu unterscheiden. Betrachten wir
das HIV-Screening einmal aus der Perspektive des
Nullhypothesentestens. Die H0 postuliert hier, dass
eine Person nicht durch HIV infiziert ist. Man
erhält dennoch ein positives Ergebnis (D) und stellt
die Frage, ob dieses Ergebnis signifikant ist. Die
Wahrscheinlichkeit
p(D|H0)
des
positiven
Testergebnisses gegeben, dass die Nullhypothese
wahr ist, beträgt .0001. Dies ist ein signifikantes
Ergebnis. Daher wird die Nullhypothese
zurückgewiesen und zwar mit einem hohen Grad
von „Vertrauen“. Wie die Regel von Bayes jedoch
zeigt, ist die Wahrscheinlichkeit einer HIVInfektion gegeben ein positives Testergebnis nur .5.
Warum kommen beide Methoden zu verschiedenen
Aussagen? Die Regel von Bayes berücksichtigt die
drei Wahrscheinlichkeiten p(H1), p(D|H1) und
p(D|H2), während der Nullhypothesentest nur die
letztere Wahrscheinlichkeit berücksichtigt.
Beim
HIV-Screening
oder
anderen
Reihenuntersuchungen kennt man die Grundrate
einigermaßen genau und kann daher diese als
Apriori-Wahrscheinlichkeit einsetzen. Wenn es
sich jedoch um eine wissenschaftliche Hypothese
handelt, hat man in der Regel keine statistische
Information, welche dieser Grundrate entspricht,
und
die
Apriori-Wahrscheinlichkeit
wird
notwendig subjektiven Charakter haben. Die
mögliche
Beliebigkeit
subjektiver
Wahrscheinlichkeiten war das Ziel von R. A.
Fishers Attacke gegen die Verwendung der Regel
von
Bayes
für
die
Bestimmung
der
Wahrscheinlichkeit von Hypothesen.
Zurück zu Thomas Bayes. Der Historiker der
Statistik, Stephen M. Stigler (2001), hat einmal ein
Gesetz über den Ursprung von Erkenntnissen
aufgestellt, das er Law of Eponymy nannte. Dieses
Gesetz besagt, dass keine wissenschaftliche
Entdeckung nach ihrem ursprünglichen Entdecker
benannt ist. Das Theorem von Pythagoras wurde
nicht von Pythagoras entdeckt, Pascals Dreieck
stammt nicht von Pascal, und die Gaußsche
Verteilung wurde auch nicht von Gauß entdeckt.
Die Regel von Bayes scheint keine Ausnahme zu
sein. In einer spannenden Detektiv-Geschichte
berechnete Stigler eine Wahrscheinlichkeit von
drei zu eins, dass tatsächlich Nicholas Saunderson
und nicht Thomas Bayes die Regel entdeckt hat.
Saunderson, der seit seinem ersten Lebensjahr
vollständig blind war und Optik lehrte, hatte den
begehrten „Lucasian Chair of Mathematics“ in
Cambridge inne, den vor ihm Newton hatte. Er
starb im Jahre 1739. Man kann Bayes jedoch nicht
die weniger höfliche (und falsche) Interpretation
von Stiglers Gesetz vorwerfen, die besagt, dass
jede wissenschaftliche Entdeckung nach der letzten
Person benannt sei, die ihre Vorgänger nicht zitiert
hat. Wie bereits erwähnt hat Bayes seine
Abhandlung ja nie veröffentlicht. Bleibt noch die
Frage: Wer entdeckte Stiglers Gesetz?
6. Die erste Nacht im Paradies
Der erste Tag im Paradies geht zu Ende. Adam und
Eva legen sich zur Ruhe. Sie hatten am Tag die
Sonne aufgehen sehen und sie bewundert, wie sie
am Himmel ihre Bahn zog und all die herrlichen
Bäume, Blumen und Vögel beschien. Irgendwann
wurde es aber kühler, während die Sonne unter
dem Horizont verschwand. Würde es jetzt auf ewig
dunkel bleiben? Adam und Eva fragen sich
sorgenvoll, welche Chance sie wohl haben, dass die
Sonne wieder aufgeht?
Im Nachhinein könnten wir vermuten, dass Adam
und Eva sicher waren, dass die Sonne wieder
aufgeht. Aber sie hatten die Sonne ja erst einmal
am Firmament emporsteigen sehen. Was also
konnten sie erwarten? Die klassische Antwort auf
dieses Problem wurde im Jahre 1812 von dem
französischen Mathematiker Pierre Simon de
Laplace gegeben.
Wenn Adam und Eva die Sonne niemals hätten
aufgehen sehen, würden sie für beide möglichen
Ereignisse (das Wieder-Aufgehen und das DunkelBleiben) gleiche Wahrscheinlichkeiten ansetzen.
Daher würden sie - für das Wieder-Aufgehen der
Sonne - einen weißen Stein in einen Beutel stecken,
außerdem einen schwarzen Stein für das Dunkel7
Bleiben. Aber sie hatten ja schon einmal gesehen,
wie die Sonne aufging, und legten deshalb einen
weiteren weißen Stein in den Beutel. Dort lagen
jetzt also zwei weiße Steine und ein schwarzer. Das
bedeutet, ihr Überzeugungsgrad, dass die Sonne
1
2
wieder aufgehen wird, war von
auf
gestiegen.
2
3
Nach dem folgenden Tag - also nach dem zweiten
Sonnenaufgang, den sie erlebten - gaben sie einen
dritten weißen Stein hinzu; nun war für sie die
Wahrscheinlichkeit für einen Sonnenaufgang von
2
3
auf
angewachsen. Laplaces Sukzessionsregel
3
4
(Regel
der
Folge)
gibt
allgemein die
Wahrscheinlichkeit p(E|n) an, dass ein Ereignis E
wieder auftritt, nachdem es n mal eingetreten ist:
p(E|n) = (n+1)/(n+2).
Ein 27-Jähriger hat in seinem Leben ungefähr
10.000 Sonnenaufgänge erlebt. Daher beträgt für
ihn der Überzeugungsgrad, dass die Sonne auch am
10.001
nächsten Tag wieder aufgeht,
. Diese
10.002
Anwendung von Laplaces Regel ist auf Kritik
gestoßen. Da die Regel von Laplace aus der Regel
von Bayes hergeleitet ist, zeigt diese Kritik
zugleich Probleme mit der Anwendung der Regel
von Bayes auf. Anders als bei dem HIV-Screening,
wo der Grundanteil der Infektion in der
betreffenden Population bekannt ist, konnten Adam
und Eva anfangs keinen Grundanteil der
Sonnenaufgänge kennen. Sie konnten also nicht
wissen, wie viele weiße oder schwarze Steine sie
am ersten Abend in den Beutel stecken mussten.
Als Pessimisten hätten sie vielleicht einen weißen
und zehn schwarze Steine genommen, als
Optimisten dagegen zehn weiße und nur einen
schwarzen. Wenn man keine Informationen zum
Abschätzen der Wahrscheinlichkeiten hat, kann
man den möglichen Ereignissen oder Ergebnissen
gleich hohe Wahrscheinlichkeiten zuschreiben.
Diese Faustregel nennt man Indifferenzprinzip.
Seine Befürworter verteidigen es damit, dass die
anfängliche
Annahme
gleicher
Wahrscheinlichkeiten
umso
geringere
Auswirkungen hat, je mehr Beobachtungen man
einfließen lässt. Beispielsweise erhält man für die
Wahrscheinlichkeit, dass die Sonne morgen
aufgeht, nach zehn Jahren, also nach über 3.650
Sonnenaufgängen, praktisch denselben Wert,
unabhängig davon, ob man als Pessimist oder
Optimist begann.
Die problematische Annahme der Indifferenz hat
Laplace tatsächlich an zwei Stellen gemacht, und
man kann das sehen, wenn man die Regel von
Bayes verwendet. H1 und H2 stehen für die
Hypothesen, dass die Sonne jeden Morgen aufgeht
bzw. nicht jeden Morgen aufgeht, und D dafür,
dass Adam und Eva einen Sonnenaufgang
beobachtet haben. Dann ergibt sich die gesuchte
Wahrscheinlichkeit p(H1|D) wie folgt:
p(H1 | D) =
p(H )p(D | H )
1
1
p(H )p(D | H )  p(H )p(D | H )
1
1
2
2
Nun kennen aber Adam und Eva die Grundrate
nicht. Die Faustregel, das Indifferenzprinzip,
1
nimmt an: p(H1) = p(H2) = . Damit vereinfacht
2
sich die Regel von Bayes zu:
p(H1 | D) =
p(D | H )
1
p(D | H )  p(D | H )
1
2
Die Wahrscheinlichkeit p(D|H1) ist per Definition
1, aber die Wahrscheinlichkeit p(D|H2) ist nicht
bekannt. Hier wird das Indifferenzprinzip nochmals
1
angewandt: p(D|H2) = . Daraus erhält man
2
schließlich:
pH 1 | D 
2
.
3
Die erste Nacht im Paradies illustriert die
Problematik, die Regel von Bayes in Situationen
anzuwenden, in denen keine oder unzureichende
empirische
Daten
vorliegen.
Das
Indifferenzprinzip, so umstritten es ist, spielt auch
heute
eine
Rolle,
beispielsweise
in
Vaterschaftsprozessen.
Um die Wahrscheinlichkeit zu bestimmen, dass ein
Mann wirklich der Vater eines Kindes ist, braucht
man, wie die Regel von Bayes zeigt, eine AprioriWahrscheinlichkeit oder Grundrate. Aber was
könnte diese Apriori-Wahrscheinlichkeit sein?
Viele Laboratorien verwenden hier das Indifferenzprinzip und nehmen eine Apriori-Wahrscheinlichkeit von 50% dafür an, dass der Angeklagte
tatsächlich der Vater ist (Gigerenzer, 2002). Diese
Praxis ist umstritten, da sie voraussetzt, dass der
Angeklagte genauso wahrscheinlich der Vater ist
wie alle anderen Männer zusammen. Die Frage ist,
wie man die beiden Fehler gewichten soll, die ein
Richter machen kann: Einen Schuldigen
freizusprechen
oder
einen
Unschuldigen
verurteilen. Die französischen Mathematiker
Dennis Poisson und Pierre Laplace vertraten eine
konservative Linie - der Schutz der Gesellschaft
vor Kriminellen ist wichtiger als der Schutz des
Individuums vor falscher Verurteilung - gegen die
früheren liberalen Reformen des Philosophen und
8
Politikers Condorcet. Die Antwort auf diese Frage
trennt Liberale von Konservativen, heute wie in
den vergangenen Jahrhunderten.
7. Die Illusion von Gewissheit
Die klassische Theorie der Wahrscheinlichkeit
überkam das Streben nach absoluter Gewissheit mit
einer
epistemischen
Interpretation
von
Wahrscheinlichkeit. Das bedeutet, dass die Ursache
der Ungewissheit in der Unkenntnis des Menschen,
nicht aber in der Natur selbst gesehen wurde. Die
Vertreter der klassischen Theorie, von Pascal bis
Laplace, waren Deterministen: Sie hielten die Welt
selbst für vollständig determiniert. Gott oder seine
säkulare Version, Laplaces Superintelligenz,
braucht keine Statistik, nur wir Menschen können
ohne diese nicht auskommen. Das war auch noch
Albert Einsteins Sicht: Gott würfelt nicht. Eine
ontische Interpretation der Wahrscheinlichkeit
musste bis zur zweiten Hälfte des 19. Jahrhunderts
warten, als der Begründer der Psychophysik,
Gustav Theodor Fechner, und der Philosoph
Charles Sanders Peirce den Zufall als eine
Eigenschaft der Natur postulierten.
Die Evolution des statistischen Denkens, die ich an
sechs klassischen Problemen illustriert habe, ist vor
allem eine Entwicklung des skeptischen Denkens.
Dieses Einmaleins der Skepsis hat mehrere Seiten.
Wie Pascals Wette veranschaulicht, ist die Basis
für skeptisches Denken der Übergang vom Streben
nach Gewissheit zum vernünftigen Umgang mit
einer unsicheren Welt. Benjamin Franklin sagte
einmal, „nichts ist sicher in dieser Welt außer der
Tod und die Steuern“. Diese scherzhaft formulierte,
aber tiefe Einsicht ist auch heute noch für viele
Menschen zu schmerzhaft, um sie als Lebensgefühl
zu akzeptieren.
Das Streben nach trügerischer Gewissheit ist ein
Teil unseres emotionalen und kulturellen Erbes. Es
erfüllt die Sehnsucht nach Sicherheit und Autorität.
Die
Esoterik-Abteilungen
der
heutigen
Buchhandlungen zeugen davon, dass viele
Menschen sich nach schnellem Glauben sehnen. Zu
allen Zeiten erdachte man Glaubenssysteme, wie
Religion, Astrologie und Weissagung, die
Sicherheit und Gewissheit versprechen und in
denen die Menschen Trost finden können - vor
allem jene, die Schweres erleiden müssen.
Gewissheit ist inzwischen zu einer Ware geworden.
Sie
wird
weltweit
vermarktet:
durch
Versicherungsgesellschaften, Anlageberater und
Wahlkämpfer, aber auch in Medizin und
Pharmazie.
Im 17. Jahrhundert bestand in Europa der Erwerb
einer Lebensversicherung darin, eine Wette auf die
Lebensdauer
eines
prominenten
Bürgers
abzuschließen. Zum Beispiel ging es darum, ob der
Bürgermeister von Paris innerhalb einer
bestimmten Zeitspanne sterben würde; wenn ja,
dann konnte derjenige, der darauf gesetzt hatte,
womöglich ein kleines Vermögen gewinnen
(Daston, 1987, 1988). Das war ein Spiel wie
dasjenige des Chevalier de Méré, nicht aber eine
sittliche Verpflichtung. Heutzutage reden uns die
Versicherungsvertreter ein, dass es bei einer
Lebensversicherung um eine Absicherung gehe und
es moralisch geboten sei, sozusagen Geld auf unser
eigenes Leben zu setzen, damit die Hinterbliebenen
im Ernstfall versorgt seien. Auch politische
Parteien schüren den Drang nach Sicherheit. Vor
den Bundestagswahlen 1998 warb die CDU mit
dem Slogan „Sicherheit statt Risiko“. Solche
Versprechungen waren nicht nur vom damaligen
Kanzler Helmut Kohl und seinen Parteifreunden zu
hören - auch andere Parteien behaupteten im
Wahlkampf, Sicherheit zu bieten.
Die Illusion der Gewissheit kann erzeugt werden,
um politische oder wirtschaftliche Ziele zu
erreichen. Nehmen wir als Beispiel die
Rinderkrankheit BSE. BSE griff im Jahr 2000 in
Großbritannien, Irland, Portugal, Frankreich und
der Schweiz um sich, während die deutsche
Regierung ihr Land für BSE-frei erklärte.
„Deutsches Rindfleisch ist sicher“ – diese Phrase
wiederholten der Präsident des Bauernverbandes,
der Landwirtschaftsminister und eine ganze
Beamtenschar unentwegt. Die Deutschen hörten
das nur zu gerne. Der Import von englischem
Rindfleisch wurde verboten, und man empfahl den
Verbrauchern, beim Metzger nur Fleisch von
Rindern zu verlangen, die in Deutschland gezüchtet
worden waren. In anderen Ländern, so wurde
verbreitet, seien mangelnde Sorgfalt und Kontrolle
an der Tagesordnung. Als man schließlich doch
zahlreiche BSE-Tests an deutschen Rinderherden
vornahm, zeigte sich die Erkrankung auch hier. Die
Öffentlichkeit war völlig überrascht, Minister
mussten zurücktreten, die Preise für Rindfleisch
fielen drastisch, und andere Länder verboten nun
ihrerseits den Import von deutschem Rindfleisch.
Die Regierung gestand schließlich ein, sich zu
lange an die Illusion geklammert zu haben,
deutsches Vieh sei von dieser Krankheit überhaupt
nicht betroffen. Das Spiel mit dem Versprechen
von Sicherheit ging indes weiter, nur waren die
Akteure jetzt andere. Supermärkte und Metzger
hängten Plakate auf und verteilten Broschüren, in
denen sie ihren Kunden versicherten: „Unser
9
Rindfleisch ist garantiert BSE-frei.“ Einige
begründeten diese Aussage damit, dass ihre
„glücklichen Kühe“ auf ökologischen Wiesen
weiden konnten, und andere behaupteten, ihre
Rinder seien sämtlich überprüft worden - kaum
jemand erwähnte, dass bei diesen Tests zahlreiche
Fehler auftreten. Als die Medien schließlich von
einer Kuh berichteten, die negativ getestet worden
war und dennoch BSE hatte, war die Öffentlichkeit
erneut schockiert. Wieder war eine Illusion der
Gewissheit dahin. Regierung und Supermärkte
hatten vor allem die Beruhigung der Verbraucher
im Sinn und weniger die Information über BSE.
Die Illusion von Gewissheit ist nicht immer für alle
bestimmt; zuweilen wird sie nur für ein
ausgewähltes Publikum heraufbeschworen. So
schilderte Jay Katz, Juraprofessor an der Yale
University, einmal eine Diskussion mit einem
befreundeten Chirurgen. Das Gespräch drehte sich
um die Ungewissheiten bei der Behandlung von
Brustkrebs. Beide waren sich darin einig, dass
niemand weiß, wie die optimale Therapie aussieht.
Katz fragte seinen Freund, wie er seine
Patientinnen berät. Der Chirurg antwortete, er habe
erst kürzlich einer Patientin mit Brustkrebs
dringend eine Radikaloperation als beste Therapie
empfohlen. Katz hielt seinem Freund vor, sich
widersprüchlich zu verhalten: Wie könne er
plötzlich so sicher sein, was die optimale
Therapieform sei? Der Chirurg gab zu, die
Patientin kaum zu kennen, beharrte aber darauf,
dass seine Patientinnen die Ungewissheit über die
beste Therapie weder verstehen noch hinnehmen
würden, wenn sie davon wüssten. Wenn man dieser
Ansicht folgt, dann wünschen die Patientinnen die
Illusion der Gewissheit, und diese Patientin bekam
sie auch.
Können moderne Technologien den Rest an
Unsicherheit nicht bald beseitigen und Sicherheit
endlich herstellen? Auch dies ist eine verbreitete
Illusion. Moderne HIV-Tests zählen beispielsweise
zu den besten medizinischen Tests. Wie wir
gesehen haben, ist dennoch - wegen der kleinen
Grundrate
von
HIV-Infizierten
ohne
Risikoverhalten - nur etwa eine von zwei Personen,
die positiv testen, tatsächlich infiziert. Die FalschNegativ-Rate liegt bei HIV-Tests bei nur etwa
0,1%; dennoch ist in der Literatur der Fall eines
amerikanischen Bauarbeiters bekannt, der 35mal
negativ testete, obgleich er mit dem Virus infiziert
war. Medizinische Tests sind nicht absolut sicher,
und das gleiche gilt für forensische Evidenz wie
Fingerabdrücke,
DNS-Profile
und
andere
genetische Tests (Gigerenzer, 2002).
8. Empirisches Denken als
Lebensgefühl
Das Grundmotiv des skeptischen Denkens ist die
Abnabelung vom Ideal sicheren Wissens. Die
zweite Motivation ist eine intellektuelle Neugierde,
die nicht bereit ist, Überzeugungen einfach
beizubehalten oder abzulehnen, sondern diese
aufgrund empirischer Evidenz bewerten möchte.
Dies erfordert den Übergang von einer politischemotionalen Lebenshaltung, in der Meinungen
durch die soziale Gruppe bestimmt sind, zu einem
statistischen Lebensgefühl. Dieses ist relativ neu,
da für viele Bereiche des menschlichen Lebens
empirische Daten früher kaum vorhanden waren
oder auch nicht gesucht wurden. John Arbuthnots
statistischer Test war, trotz seiner offensichtlichen
Mängel, ein früher Schritt in die Richtung,
Überzeugungen durch Evidenz zu testen.
Im 18. und 19. Jahrhundert waren statistische
Informationen meist Staatsgeheimnisse, die nur
einer Elite bekannt waren und der Öffentlichkeit
vorenthalten wurden. Die Bedeutung statistischer
Informationen, etwa von Bevölkerungszahlen,
wurde aber von den politisch Verantwortlichen
erkannt. Napoleons Gier nach Daten aus seinem
bureau de statistique war legendär (Bourget, 1987).
Und er wollte die Zahlen immer sofort haben. In
seiner Umgebung hieß es: Wenn du etwas von
Napoleon willst, gib ihm Statistiken. Die
Bereitschaft, wirtschaftliche und demographische
Daten der Öffentlichkeit zugänglich zu machen, ist
dagegen jüngeren Datums. Erst ab etwa 1830
wurden Statistiken veröffentlicht, zumindest einige.
Seitdem hat eine „Lawine gedruckter Zahlen“, wie
sich der Philosoph Ian Hacking ausdrückte, die
heutige Welt in einen gewaltigen Ozean von
Informationen verwandelt, der von Medien wie
Fernsehen und Zeitschriften sowie vom Internet
gespeist wird. Die zunehmende Verbreitung
statistischer Informationen im 19. und 20.
Jahrhundert korrelierte mit dem Aufkommen der
Demokratien in der westlichen Welt.
9. Statistisches Denken statt
statistischer Rituale
Statistisches Denken ist nicht nur skeptisch
gegenüber der Illusion von Gewissheit, sondern
auch gegenüber dem Umgang mit Statistik selbst.
Es ist nützlich, zwei Umgangsweisen zu
unterscheiden: statistisches Denken und statistische
Rituale. Statistisches Denken ist selbstreflektiv; es
beinhaltet die Abwägung, welche Methode oder
welches Modell für eine Situation die beste ist und
10
unter welchen Annahmen das gilt. Beispielsweise
macht Laplaces Geschichte von der ersten Nacht
im Paradies deutlich, dass die Anwendung der
Regel von Bayes besser zu rechtfertigen ist, wenn
man empirische Informationen über die Grundraten
und die Wahrscheinlichkeiten hat, als wenn das
nicht der Fall ist. Richter lassen heute die Regel
von Bayes in Strafprozessen nur zu, wenn
empirische Informationen vorhanden sind, und
dann auch nicht immer. John Arbuthnots
Gottesbeweis illustriert dagegen die Probleme und
Grenzen des Nullhypothesentestens.
Statistische Rituale sind heute in den
Sozialwissenschaften weit verbreitet - anders als in
der molekularen Biologie, der Kernphysik oder den
anderen naturwissenschaftlichen Disziplinen, wo
diese nie Fuß fassen konnten. Wenn auf jedes
Problem ein- und dieselbe Methode unreflektiert
angewendet wird, dann haben wir ein statistisches
Ritual vor uns. Beispielsweise berechnet man in
manchen Bereichen der pädagogischen Psychologie
mechanisch Pfadanalysen, in Bereichen der
Persönlichkeitspsychologie ebenso mechanisch
Faktorenanalysen und in der experimentellen
Sozialpsychologie
erinnert
das
ständige
Nullhypothesentesten
an
zwanghaftes
Händewaschen. Jede Disziplin hat ihr eigenes
statistisches „Überich“, das bei ihren Mitgliedern
Verhaltensweisen erzeugt, die an eine Neurose
erinnern. Man fühlt den Druck, die Methode
anwenden zu müssen, denn ohne sie fühlt man sich
nackt. Nur ein geringer Prozentsatz der
akademischen Psychologen versteht überhaupt, was
ein signifikantes Ergebnis bedeutet oder was man
daraus schließen kann. Das gilt selbst für Dozenten,
die Statistik für Psychologen lehren (Oakes, 1986;
Haller & Krauß, 2002). Viele glauben
irrtümlicherweise, ein signifikantes Ergebnis - wie
bei Arbuthnot - würde die Wahrscheinlichkeit
angeben, dass die Nullhypothese richtig sei oder
dass die Alternativhypothese falsch sei. Anders als
die Regel von Bayes kann jedoch ein
Nullhypothesentest keine Wahrscheinlichkeit für
Hypothesen
erbringen,
lediglich
eine
Wahrscheinlichkeit für die Daten unter der
Annahme, dass die Nullhypothese wahr ist.
Alternative statistische Methoden, wie NeymanPearson Hypothesentests, Walds Sequentielle
Tests, Tukeys „exploratory data analysis“ oder
Bayes’ Statistik, sind kaum bekannt, und es besteht
auch geringes Interesse, diese kennen zu lernen.
Statistiker wie R. A. Fisher und Jerzy Neyman
haben die gedankenlose Anwendung ein- und
derselben statistischen Methode immer wieder
kritisiert, aber die Betroffenen scheinen dies nicht
bemerkt oder schlicht verdrängt zu haben
(Gigerenzer, 1993; Gigerenzer et al., 1999).
Die Evolution des statistischen Denkens hat nicht
nur Probleme gelöst, sie hat auch neue Probleme
erzeugt. Mit der Entwicklung der Theorie der
Wahrscheinlichkeit wurde die Vielfalt von
Konzepten, die im begrifflichen Umfeld von Zufall
und Erwartung stand, auf einige ganz wenige
eingeengt. Der Begriff „probabilitas“ bedeutete
ursprünglich eine durch Autorität gesicherte
Meinung. Dieses Konzept wurde nicht zum
Gegenstand der Theorie, genauso wenig wie die
nahe liegenden Kandidaten Glück und Schicksal.
Die drei Interpretationen von Wahrscheinlichkeit,
mit der die Theorie begann, sind noch heute oft
miteinander in Konflikt. Ist Wahrscheinlichkeit
eine relative Häufigkeit in einer Referenzklasse von
Ereignissen wie in statistischen Tabellen? Oder ist
sie der Grad der subjektiven Überzeugung, die eine
vernünftige Person hat? Oder ist sie durch das
Design bestimmt wie die Konstruktion eines
Würfels? Diese Frage trennt die Frequentisten, wie
Richard von Mises und Jerzy Neyman, von den
subjektiven Bayesianern, wie De Finetti und
Leonard Savage, und von den Vertretern von
Propensitäten wie Karl Popper. Die Antwort auf
diese Frage bestimmt den Gegenstandsbereich der
Theorie. Für einen Subjektivisten ist dieser
unbegrenzt; alles in der Welt, wozu Menschen
Überzeugungen haben, die den Gesetzen der
Theorie folgen, ist möglicher Gegenstand. Dies
schließt Wahrscheinlichkeiten für Einzelfälle mit
ein, selbst für Ereignisse, die noch nie beobachtet
wurden, wie die erstmalige Anhebung der
Lebenserwartung auf mehr als 100 Jahre. Für einen
Frequentisten bezieht sich die Theorie nur auf
Aussagen über Elemente einer Referenzklasse, die
als untereinander gleich angesehen werden können
und für die hinreichend viel statistische
Information vorliegt. Aus dieser Sicht ist die
Theorie auf Situationen wie dem HIV-Screening
anwendbar, wo genügend Daten vorliegen, nicht
aber auf die erste Nacht im Paradies. Aus der Sicht
der Wahrscheinlichkeit als Propensität (Design) ist
der Anwendungsbereich der Theorie noch kleiner:
Sie betrifft nur Gegenstände, deren Bauplan oder
kausale Struktur wir kennen.
Diese verschiedenen Auslegungen des Begriffs
Wahrscheinlichkeit
können
unterschiedliche
Abschätzungen des jeweiligen Risikos hervorrufen.
Vor einigen Jahren nahm ich an einer Führung
durch ein Werk der DASA (Daimler Benz
Aerospace) teil, in dem die Ariane-Rakete
hergestellt wird, die Satelliten in ihre Umlaufbahn
11
befördert. Ich stand mit dem Führer vor einem
großen Plakat, auf dem alle bis dahin
abgeschossenen 94 Raketen (Ariane, Modelle 4
und 5) aufgeführt waren, und fragte ihn, wie hoch
das Risiko eines missglückten Starts sei. Er
erwiderte, der Sicherheitsfaktor betrage etwa
99,6%. Das erschien mir überraschend hoch, denn
auf dem Plakat sah ich acht Sterne, die für acht
Unfälle standen. Ich fragte also, wie acht Unfälle
von 94 Starts einem Sicherheitsfaktor von 99,6%
entsprechen könnten. Daraufhin erklärte er, die
DASA zähle nicht die Fehlstarts, sondern berechne
den Sicherheitsfaktor aus der Konstruktion der
einzelnen Teile der Rakete. Die Fehlstarts zu
zählen würde menschliches Versagen einbeziehen.
Er fügte hinzu, dass beispielsweise einer dieser
Sterne letztlich auf ein Missverständnis
zurückgehe, nämlich zwischen einem Arbeiter, der
eine Schraube weggelassen hatte, und seinem
Kollegen von der nächsten Schicht, der annahm,
sein Vorgänger habe die Schraube eingesetzt.
Somit beruhte das genannte Risiko von Fehlstarts
der Ariane-Raketen auf einer Design-Interpretation
und nicht auf den tatsächlichen Häufigkeiten.
10.Vom Mut, sich seines eigenen
Verstandes zu bedienen
Statistisches Denken ist ein Produkt der Zeit der
Aufklärung. Der Philosoph Immanuel Kant begann
seinen im Jahre 1784 verfassten Aufsatz „Zur
Beantwortung der Frage: Was ist Aufklärung?“
folgendermaßen:
Aufklärung ist der Ausgang des Menschen aus
seiner selbst verschuldeten Unmündigkeit.
Unmündigkeit ist das Unvermögen, sich seines
Verstandes ohne Leitung eines anderen zu
bedienen. Selbstverschuldet ist diese Unmündigkeit, wenn die Ursache derselben nicht
am Mangel des Verstandes, sondern der
Entschließung und des Mutes liegt, sich seiner
ohne Leitung eines anderen zu bedienen.
Sapere aude! Habe Mut, dich deines eigenen
Verstandes zu bedienen! ist also der
Wahlspruch der Aufklärung.
Das sind klare und tiefe Gedanken. Der
Schlüsselbegriff ist „Mut“. Dieser ist notwendig,
weil man sich mit Hilfe des eigenen Verstandes
nicht nur die Gefühle der Befreiung und der
Selbstständigkeit verschaffen kann, sondern weil
auch Strafe und Schmerz die Folge sein können.
Kant selbst musste das erfahren. Einige Jahre
nachdem er diese Sätze niedergeschrieben hatte,
verbot ihm die Obrigkeit - aus Furcht, sein
rationales Denken könne die Sicherheit der
christlichen Lehre untergraben - weiterhin über
religiöse Themen zu schreiben oder zu lehren.
Ganz allgemein kann das Überwinden der
Unmündigkeit bedeuten, dass man Lücken oder
Widersprüche in Berichten, Tatsachen und
Wertvorstellungen findet, an die man immer
geglaubt hatte. Das Hinterfragen von Gewissheiten
bedeutet oft das Hinterfragen von gesellschaftlicher
Autorität.
Mit Ungewissheiten leben zu lernen, stellt für
Einzelne wie auch für Gesellschaften eine große
Herausforderung dar. Ein großer Teil unserer
Geschichte wurde von Menschen geprägt, die sich
völlig sicher waren, dass ihre Sippe, Rasse oder
Religion die von Gott oder vom Schicksal erwählte
war - und die für sich daraus das Recht ableiteten,
abweichende Ideen zu bekämpfen wie auch die
Menschen, die davon „befallen“ waren. Es war ein
langer Weg zu den heutigen Gesellschaftsformen
mit größerer Toleranz gegenüber Ungewissheit und
Vielfalt. Trotzdem sind wir noch weit davon
entfernt, die mutigen und informierten Menschen
zu sein, die Kant vor Augen hatte - ein Ziel, das
sich in zwei schlichten lateinischen Wörtern
ausdrücken lässt: Sapere aude. Habe den Mut,
selbst zu denken.
Erstveröffentlichung
Gigerenzer, G. (2004). Die Evolution des
statistischen Denkens. In Unterrichtswissenschaft – Zeitschrift für Lernforschung, 32. Jahrgang, Heft 1, S. 4 – 22. Weinheim: Juventa
Literatur
Arbuthnot, J. (1710). An argument for divine
providence, taken from the constant regularity
observ’d in the birth of both sexes. Philosophical Transactions of the Royal Society, 27, 186190.
Bayes, T. (1763). An essay towards solving a problem in the doctrine of chances. Philosophical
Transactions of the Royal Society, 53, 370-418.
Übersetzung von: H. E. Timmerding (1908).
Versuch zur Lösung eines Problems der
Wahrscheinlichkeitsrechnung. Leipzig: Wilhelm
Engelmann (Oswalds Klassiker der exakten
Wissenschaften, 169).
Bernoulli, D. (1738). Specimen theoriae novae de
mensura sortis. Commentarii academiae
scientarum imperialis Petropolitanae, 5, 175192. Englische Übersetzung von: L. Sommer
(1954). Exposition of a new theory on the
measurement of risk. Econometrica, 22, 23-36.
12
Bourguet, M.-N. (1987). Décrire, compter, calculer:
The debate over statistics during the Napoleonic period. In L. Krüger, L. Daston & M. Heidelberger (Eds.), The probalistic revolution: Vol I.
Ideas in history (pp. 305-316). Cambridge, MA:
MIT Press.
Daston, L. (1987). The domestication of risk: Mathematical probability and insurance 1650-1830.
In L. Krüger, L. Daston & M. Heidelberger
(Eds.), The probabilistic revolution: Vol. I. Ideas
in history (pp. 237-260). Cambridge, MA: MIT
Press.
Daston, L. (1988). Classical probability in the enlightenment. Princeton, NJ: Princeton University Press.
Fisher, R. A. (1935). The design of experiments.
Edingborgh: Oliver and Boyd.
Gigerenzer, G. (1993). Über den mechanischen
Umgang mit statistischen Methoden. In E. Roth
(Hg.), Sozialwissen-schaftliche Methoden (3.
Aufl., S. 607-618). München: Oldenbourg.
Gigerenzer, G. (2002). Das Einmaleins der Skepsis.
Berlin: Berlin Verlag.
Gigerenzer, G., Hoffrage, U., & Ebert, A. (1998).
AIDS counseling for low-risk clients. AIDS
CARE, 10, 197-211.
Gigerenzer, G., Swijtink, Z., Porter, T., Daston, L.,
Beatty, J., & Krüger, L. (1999). Das Reich des
Zufalls. Heidel-berg: Spektrum.
Hacking, I. (1975). The emergence of probability.
Cambridge, MA: Cambridge University Press.
Hacking, I. (1990). The taming of change. Cambridge, MA: Cambridge University Press.
Haller, H., & Krauss, S. (2002). Misinterpretations of
significance: A problem students share with
their teachers? Methods of Psychological Research Online, 7, 1-20.
Jorland, G. (1987). The St.-Petersburg-Paradox,
1713-1937. In L. Krüger, L. Daston & M. Heidelberger (Eds.), The probabilistic revolution:
Vol. I. Ideas in history (pp. 157-190).
Cambridge, MA: MIT Press.
Krüger, L., Gigerenzer, G., & Morgan, M. (Eds.).
(1987). The probabilistic revolution: Vol. II. Ideas in the sciences. Cambridge, MA: MIT Press.
Laplace, P. S. (1812). Théorie analytique des probabilités. Paris: Courcies.
Montmort, P. R. de. (1713). Essai d’analyse sur les
jeux de hasard (2. Aufl.). Paris.
Pascal, B. (1654/1970). Briefwechsel PascalFermat. In B. Pascal, Œuvres complètes (S.
1136-1158), hg. von Jean Mesnard (Œuvres
diverses,
Bd.
1).
Paris:
Bibliothèque
Européenne - Desclès de Brouwer.
Pascal, B. (1669/1904). Pensées. Hg. von Léon
Brunschwicg (3 Bde.). Paris: Librairie Hachette.
Deutsche Überset-zung von: W. Rüttenauer
(1937). Gedanken. Leipzig: Dieterich’sche Verlagsbuchhandlung.
Oakes, M. (1986). Statistical inference: A commentary for the social and behavioral sciences.
New York: Wiley.
Stigler, S. M. (1983). Who discovered Bayes theorem? American Statistician, 37, 290-196.
Anschrift des Verfassers
Prof. Dr. Gerd Gigerenzer
Max-Planck-Institut für Bildungsforschung
Lentzeallee 94, 14195 Berlin
[email protected]
13
Wie gut kannst Du schätzen?
Und andere Probleme für den Statistik-Unterricht
HELMUT W IRTHS, OLDENBURG
Zusammenfassung: Es geht in diesem Beitrag um
Unterrichtseinheiten, bei denen schnell Daten
gewonnen oder bereitgestellt werden können,
außerdem um Fragen, die sich Lernenden geradezu
aufdrängen, und die sie geklärt wissen wollen. Wie
sich
dabei
Begriffe,
Methoden
und
Darstellungsarten der Statistik, auch die der
explorativen Datenanalyse einsetzen lassen, wird
in diesem Beitrag dargestellt, ebenso Hilfen, die
ein zumindest graphikfähiger Taschenrechner
bietet.
Aufgabe:
Die folgende Liste enthält die Namen von 14
bekannten Persönlichkeiten des öffentlichen
Lebens. Notiere das von Dir geschätzte Alter jeder
Person, ohne mit jemanden darüber zu sprechen.
Wenn Dir die Person unbekannt ist, versuche zu
raten.
Person
Alter (geschätzt)
Franziska von Almsick
Franz Beckenbauer
1. Einführung
Seit dem Schuljahr 2003/2004 gelten in
Niedersachsen
neue Richtlinien für den
Mathematikunterricht in den Klassen 7 bis 10 des
Gymnasiums. Für die Jahrgangsstufen 7 und 8 ist
ein
Lehrplanelement
enthalten,
in
dem
Statistikunterricht gefordert wird. Es soll dabei die
Datenkompetenz der Lernenden gefördert und in
statistisches Denken eingeführt werden. Zwar
haben die Richtlinien für die Orientierungsstufe für
Klasse 5 ebenfalls den Umgang mit Daten
gefordert, doch konnte ich davon in Klasse 7 nichts
feststellen. In der Regel wurde dieser Teil der
Richtlinien dem Refrain eines Songs von Hans
Scheibner folgend („Das macht doch nichts, das
merkt doch keiner.“) gar nicht erst unterrichtet. Da
auch für das Gymnasium keine Fortsetzung
vorgesehen war, wird Unterricht in Statistik für
viele Lehrende neu sein. In diesem Beitrag werden
Anregungen gegeben, wie Statistik unterrichtet
werden kann.
2. Schätzen des Alters bekannter
Persönlichkeiten
Engel [2001] habe ich die folgende Aufgabe
entnommen und in mehreren Lerngruppen erprobt.
Wer meint, die eine oder andere Persönlichkeit sei
in seiner Lerngruppe zu wenig bekannt, setze dafür
eine bekanntere ein und behalte dabei die
Mischung zwischen jüngeren und älteren Personen
bei.
Bill Clinton
Heike Drechsler
Thomas Gottschalk
Nelson Mandela
Queen Elizabeth II
Christina Rau
Claudia Schiffer
Michael Schumacher
Arnold Schwarzenegger
Katja Seizinger
Wolfgang Thierse
Jan Ullrich
Soweit die Aufgabenstellung. Alle 14 Schätzungen
sind schnell gemacht. Lernende wollen unbedingt
wissen, ob sie gut geschätzt haben. Es entwickelt
sich auch die Frage nach der besten Schätzung in
der Lerngruppe. Um das zu entscheiden, müssen
die Lernenden selbständig Kriterien entwickeln. In
einer Lerngruppe wird das folgendermaßen
formuliert: „Im Fußball wird die Rangfolge durch
die erreichte Punktzahl festgelegt. Wer mehr
Punkte hat, bekommt einen besseren Rangplatz.
Bei
gleicher
Punktzahl
entscheidet
die
Tordifferenz, bei gleicher Tordifferenz die größere
Anzahl der geschossenen Tore. Bei unserer
Schätzaufgabe ist es so: Die Anzahl der richtigen
Schätzungen legt die Reihenfolge fest. Aber wir
Stochastik in der Schule 24 (2004) Heft 2, S. 14 – 23
14
brauchen noch ein weiteres Kriterium, das die
Reihenfolge bei gleicher Anzahl an richtigen
Schätzungen regelt.“ Ein zumindest graphikfähiger
Taschenrechner
kann
die
Situation
veranschaulichen. Zeichnen wir ein Streudiagramm
und tragen auf der x-Achse das wahre Alter und auf
der y-Achse das geschätzte Alter ab. Richtige
Schätzungen liegen auf der Gerade mit der
Gleichung y = x, die wir noch zusätzlich
einzeichnen. Die Schätzungen von Anke, Beate und
Jan sind im folgenden Bild dargestellt
Die Symbole bedeuten:  stellt die Schätzungen
von Jan,  die von Beate und  die von Anke dar.
Man kann diesem Bild schon Hinweise entnehmen,
wie die drei Personen schätzen. Wir unterstützen
den Prozess, ein Kriterium zu finden, und stellen
die Abweichungen des geschätzten Alters vom
richtigen Alter dar. Eine negative Abweichung soll
bedeuten, dass das Alter zu niedrig geschätzt wurde, entsprechend eine positive Abweichung, dass es
zu hoch eingeschätzt wurde. Wir stellen eine neue
Liste mit den Abweichungen her. Auch dies ist
schnell geschehen, wenn wir es den Rechner durchführen lassen und im Tabellenkopf die entsprechende Gleichung eingeben. Die Abweichungen
der Schätzungen der drei Personen von den wahren
Werten ergeben folgendes Bild:
Über Abweichungen wird in dieser Lerngruppe lange diskutiert. Thomas formuliert eine erste Bedingung: Je kleiner die Summe aller Abweichungen
ist, desto besser ist die Schätzung. Seinem Beispiel
die Summe 10 sei besser als 100 setzt Katharina als
Gegenbeispiel entgegen, dass die Summe -100
nicht besser als -10 sei. Till fasst schließlich die
Diskussion zusammen: Die Summe aller Abweichungen soll Null sein. Aber dagegen erhebt sich
Widerstand aus der Lerngruppe. Dies Kriterium
könne sowohl jemanden erfassen, der immer ganz
schlecht schätzt, mal viel zu groß, ein anderes Mal
viel zu klein, aber auch jemand, der immer nur ein
wenig die richtige Lösung verfehlt. Also eignet sich
das Kriterium „Die Summe aller Abweichungen
soll Null sein.“ nicht zur Charakterix^^sierung des
besten Schätzers.
Statistik treiben heißt auch, die Fülle der Daten auf
eine überschaubare Anzahl an Kennzahlen zu reduzieren, die immer noch möglichst viel Informationen über den Datensatz enthalten. Hier bieten
sich die folgenden fünf Kennzahlen an, die einfach
zu bestimmen und zu interpretieren sind: Das Maximum, das Minimum der Daten, der Median und
die beiden Quartile. Wie diese aus einer sortierten
Datensammlung bestimmt werden können, und wie
daraus ein Maximum-Minimum-Boxplot oder ein
Boxplot, der mögliche Ausreißern besonders
hervorhebt, gezeichnet werden kann, wird zum
Beispiel in Wirths [2002] dargestellt. Nun folgt der
Boxplot zu den Abweichungen der Schätzungen
der drei Personen von den wahren Werten:
15
Nach Meinung der Lerngruppe treten bei den Boxplots die Eigenheiten der drei Personen beim Schätzen besonders deutlich hervor. Alle schätzen mal
zu viel, ein andermal zu wenig. Beate neigt stärker
zum Unterschätzen, Anke zum Überschätzen, während Jans Schätzungen (fast) ausgeglichen erscheinen. Meine Frage an die Lerngruppe: Wie sieht ein
Boxplot für Jemanden aus, der immer unter-(über)schätzt, und wie für eine Person, bei der sich Unterund Überschätzungen ideal ausgleichen?
Bei der Diskussion, ob über die Abweichungen ein
Kriterium für gute Schätzungen entwickelt werden
kann, habe ich gehofft, dass aus der Lerngruppe
heraus der Vorschlag kommt, die Abstände, also
die Beträge der Abweichungen, zu betrachten, habe
mich aber bewusst zurückgehalten. In dieser Lerngruppe kommt dieser Vorschlag erst jetzt nach der
ausgiebigen Diskussion über Abweichungen. Wir
stellen eine neue Liste mit den Abständen her.
Auch dies ist schnell geschehen, wenn wir es den
Rechner durchführen lassen und im Tabellenkopf
die entsprechende Gleichung eingeben. Nach den
Erfahrungen mit den Abweichungen drucke ich
hier kein Streudiagramm ab, sondern sofort die
Boxplots der Abstände der Schätzungen der drei
Personen von den wahren Werten:
Anke und Jan haben jeweils eine richtige
Schätzung, während Beates beste Schätzung um ein
Jahr vom richtigen Alter abweicht. Das kann man
zwar auch schon am ersten Streudiagramm
erkennen, aber nach Meinung meiner Lerngruppen
wird es bei den Boxplots am deutlichsten. Anke
und Beate haben aber auch jeweils eine Schätzung
(in ihrem Boxplot mit „“) gekennzeichnet, die
weit außerhalb des Bereichs ihrer übrigen
Schätzungen liegt, also einen Ausreißer im Sinne
der Statistik darstellt. Meine Schülerinnen und
Schüler haben anstelle von Ausreißer von einer
außerordentlich schlechten Schätzung gesprochen.
Für Jan als besten Schätzer sprechen nach Meinung
der Lerngruppe folgende statistischen Kennzahlen:
Er hat den besseren Median, das bessere 3. Quartil
und das niedrigste Maximum, während er im
Minimum nicht schlechter als Anke und im 1.
Quartil nicht schlechter als Anke und Beate ist.
Außerdem ist bei Jan die Summe aller Abstände
minimal. Und damit ist in dieser Lerngruppe das
zweite Kriterium gefunden, das neben der Zahl der
richtigen Lösungen den besten Schätzer charakterisieren soll.
In anderen Lerngruppen ist die minimale Summe
der Abstände das dominierende Kriterium. Jannes
stellt das zum Beispiel so dar: Wenn jemand vier
richtige Lösungen hat, weicht aber bei den
restlichen Schätzungen zum Teil erheblich von den
richtigen Werten ab, dann hat er schlechter geschätzt als jemand, der drei richtige Lösungen hat
und sich sonst immer nur um ein bis höchstens
zwei Jahre verschätzt. Für die Lerngruppe um
Jannes gilt die minimale Summe aller Abstände als
einziges Kriterium. Ich habe auch hier nicht
regulierend oder formend ins Gespräch eingegriffen. Mir ist es wichtig, dass die Lernenden
selbständig Ideen entwickeln und eigenständig Kri-
16
terien über den besten Schätzer unter sich aushandeln und dann konsequent anwenden.
3. Die Euro-Scheine
Nach Behandlung des arithmetischen Mittelwerts,
der fünf Kennzahlen der EDA und der beiden Boxplot-Typen bringen die Lernenden einer 8. Klasse
unvermutet folgende Fragen in den Unterricht ein
und wollen sie unbedingt behandelt wissen:
Welche Euro-Scheine und Euro-Münzen gibt es?
Welche davon sind in der eigenen Geldbörse oder
in der der Eltern vorhanden?
Die Schülerinnen und Schüler schauen zunächst in
der eigenen Geldbörse nach, befragen dann
Freunde, Eltern sowie weitere Bekannte und tragen
ihre Ergebnisse zusammen. Jeder stellt seine
Ergebnisse unter der Überschrift „Verteilung der
Euro-Münzen und -Scheine in der Geldbörse von
...“ (hier folgt der Name oder auch ein Pseudonym,
manchmal werden ganz penibel Datum und Uhrzeit
mit vermerkt) für jede Geldbörse in einem eigenen
Histogrammen dar. Auf der waagerechten Achse
wird der Münz- bzw. der Geldscheinwert in aufsteigender Reihenfolge im Abstand von 0,5 cm aufgetragen, auf der dazu senkrechten Achse die Anzahl
der vorgefundenen Exemplare der jeweiligen Sorte.
Diese Darstellungsart ist ihnen aus dem bisherigen
Unterricht bekannt und muss auch Lesern nicht
mehr unbedingt vorgestellt werden. So unterschiedlich die von den Lernenden gezeichneten
Verteilungen auch sind (nicht immer kommt von
jeder Münzsorte oder von jeder Geldscheinsorte
wenigstens ein Exemplar zum Vorschein, mal sind
es mehr Münzen, mal mehr Scheine, der
Gesamtwert aller Scheine und Münzen schwankt
erheblich von Geldbörse zu Geldbörse, sogar die
Entdeckung ausländischer Euromünzen wird
registriert), eine Beobachtung ist deutlich: Es
fehlen Scheine mit den Werten 500 €, 200 € und
100 €. In Schülergeldbörsen wird auch der 50 €Schein selten angetroffen. „Pro Kopf sollen es
mehr als 2 000 € sein.“, sagt Lukas und beteuert,
das habe er irgendwo gelesen. „Wir sind mit
unseren
Beobachtungen
davon
meilenweit
entfernt.“ Die Lernenden wollen die Behauptung
von Lukas nachprüfen. Dem Kalender für
Lehrerinnen und Lehrer 2001/2002 aus dem
Deutschen Sparkassen Verlag können wir folgende
Angaben der Deutschen Bundesbank über die Anzahl der zum 1.1.2002 neu eingeführten EuroScheine in allen Euro-Ländern entnehmen:
Nennwert in €
Anzahl in 106 Stück
5
2 415
10
3 013
20
3 608
50
3 674
100
1 246
200
229
500
360
Außerdem sind die Motive und die Maße der einzelnen Scheine vermerkt. Der Aufforderung, so
viele Informationen wie möglich zu errechnen,
können die Lernenden nicht widerstehen und so
wird

die Gesamtzahl der Euro-Scheine,

der Gesamtwert des Papiergelds,

die Fläche des Papiergelds für jede Sorte,

die gesamte bedruckte Fläche des Papiergelds,

den auf jeden einzelnen Einwohner in den Ländern mit Euro-Währung (ca. 304 Millionen
Einwohner) im Mittel entfallenden PapiergeldBetrag,

der Anteil der einzelnen Geldscheinsorte an der
Gesamtzahl
der
Scheine
bzw.
am
Gesamtgeldwert,
 der mittleren Wert eines Euro-Scheins
berechnet. Einige versuchen auch noch, die Papiermasse abzuschätzen.
Die Behauptung von Lukas erweist sich als korrekt.
Auf jeden Einwohner in den Euro-Ländern entfällt
der immense Betrag von 2 133,10 €. Außerdem berechnen wir, dass ein Euro-Schein im (arithmetischen) Mittel 44,58 € wert ist. (Beide Beträge sind
auf volle Cent abgerundet.)
„Irgendetwas ist faul.“, sagt Ronald und setzt eine
stürmische Diskussion in Gang, in der die vorher
erarbeiteten Ergebnisse zum arithmetischen
Mittelwert in Frage gestellt werden. „Wenn ich den
Pro-Kopf-Euro-Betrag mit der Anzahl der
Einwohner multipliziere, erhalte ich nicht den
Gesamtwert aller Euro-Scheine. Das gleiche gilt für
das Produkt aus dem Mittelwert aller Scheine und
der Anzahl der Scheine.“ Haben wir gegen die
Vorstellung der gleichmäßigen Verteilung, die zum
arithmetischen Mittelwert gehört, verstoßen? Nun,
wir haben auf volle Cent gerundet. Rechnen wir bei
den Mittelwerten mit allen Stellen, die der Rechner
anzeigt, dann erhalten wir die gewünschte volle
Übereinstimmung. Dieses Beispiel zeigt, dass der
arithmetische Mittelwert von Geldbeträgen nicht
unbedingt ein Geldbetrag ist. Aber dass das
17
Runden einen Fehlbetrag von 48,9 Millionen Euro
(Mittelwert pro Euro-Schein auf Cent gerundet
multipliziert mit der Zahl aller Scheine) ergibt, das
beeindruckt sie doch sehr.
Schließlich wollen die Lernenden auch noch die 5
Kennzahlen der EDA berechnen und beide
Boxplots zeichnen. Dazu denken wir uns alle
14,545109 Euro-Scheine dem Wert nach in aufsteigender Folge sortiert. Die 5 Kennzahlen erhalten
wir wie folgt:
Minimum
Wert des 1. Geldscheins (5 €)
1. Quartil
Mittelwert der Werte des 3 636
250 000. Scheins und des 3 636
250 001. Scheins (10 €)
Median
Mittelwert der Werte des 7 272
500 000. Scheins und des 7 272
500 001. Scheins (20 €)
3. Quartil
Mittelwert der Werte des 10 908
750 000. Scheins und des 10 908
750 001. Scheins (50 €)
Maximum
Wert letzter Schein (500 €)
Wenn wir einen Boxplo t zeichnen, fällt auf, dass
der untere Whisker (Länge 5 €) im Vergleich zum
oberen (Länge 450 €) extrem lang ist. Das weckt
Interesse an einem Boxplot der beurteilenden
Statistik. Wir rechnen: R = Q3 - Q1 = 40 € und
1,5R = 60 €. Daraus folgt: Q1 - 1,5R = -50 €.
Nach unten gibt es also keine Ausreisser. Der
untere Whisker reicht von 5 € bis 10 €. Ferner gilt:
Q3 + 1,5R = 110 €, der obere Whisker reicht daher
von 50 € bis 100 €. Die Werte der Geldscheine zu
200 € und 500 € liegen „weit außerhalb“ des Bereichs, der durch die Whisker dargestellt wird, sind
also Ausreisser. Insgesamt sind das rund 4 % aller
Geldscheine. Statt von Ausreißern reden die
Schülerinnen und Schüler von außergewöhnlichen
Geldscheinen, die man in normalen Geldbörsen in
der Regel nicht oder nur ganz selten, und dann nur
zu besonderen Anlässen, findet.
4. Ein Weitsprungwettbewerb
Das folgende Beispiel eignet sich ebenfalls gut als
Einführung in statistisches Denken. Bei solchen
Wettbewerbssituationen kann man Lernende leicht
zum Formulieren von Leitfragen bewegen. Das
Problem lautet:
Die Klassen 7a und 7b machen einen Wettbewerb
im Weitsprung. Die Ergebnisse in Meter sind:
Lerngruppe 7a:
2,92; 3,60; 3,47; 3,50; 3,54; 3,06; 3,08; 3,12; 3,16;
3,18; 3,17; 3,23; 3,19; 3,16; 3,36; 3,42; 3,40; 3,38;
3,37; 3,39; 3,28; 3,27; 3,34; 3,35; 3,31; 3,32; 3,30;
3,33; 3,29
Lerngruppe 7b:
3,41; 3,40; 3,42; 3,39; 3,43; 3,41; 3,02; 3,80; 3,47;
3,47; 3,53; 3,55; 3,50; 3,12; 3,07; 3,70; 3,75; 3,25;
3,20; 3,17; 3,57; 3,62; 3,65; 3,35; 3,35; 3,29; 3,27;
3,32
Aufgaben:
1. Welche Klasse die „bessere“?
2. Welche Klasse ist die „ausgeglichenere“?
3. Welche Klasse hat die „stärkere Spitze“?
4. In welcher Klasse ist eine Leistung von 3,50 m
„mehr wert“, das heißt in welcher Klasse
gehört man mit dieser Sprungweite zu den
besseren Sportlern dieser Klasse?
Lösungsskizzen zu 1:
In der Regel wird der Vergleich der arithmetischen
Mittelwerte der Sprungweiten von Lernenden als
Kriterium genannt. In der 7a ist das arithmetische
Mittel 3,29 m, in der 7b ist es 3,41 m. Damit kann
man sich begnügen und die 7b als die bessere
Klasse bezeichnen. Ich wollte das auch, musste
aber umdisponieren, als Florian sein Unbehagen
äußert: „Wenn in die 7a ein Springer hinzukommt,
der erheblich weiter als alle anderen springt, dann
kann sich unser Urteil ändern.“ Und Florian macht
an einigen Beispielen klar, wie sich der
arithmetische Mittelwert ändert, wenn wir einen
besonders starken Springer (also einen Ausreißer
im Sinne der Statistik) hinzunehmen. Eins macht
die Diskussion deutlich. Wenn wir die Daten nicht
kennen, dann müsen wir beim Vergleich von
arithmetischen Mittelwerten vorsichtig sein. Bei
unseren Daten ist die Situation überschaubar, es
gibt keinen Ausreißer. Die Diskussion hat als
Nebenergebnis gebracht, dass der Median erheblich
geringere Veränderungen erfährt als der arithmetische Mittelwert. Wenn wir die fünf Kennzahlen der
EDA berechnen, wird es noch deutlicher. Neben
dem arithmetischen Mittelwert sind 5 weitere statistische Kennzahlen (Minimum, 1. Quartil, Median,
3. Quartil, Maximum) bei Klasse 7b größer als bei
Klasse 7a. Besonders eindrucksvoll zeigt es der
Vergleich der beiden Boxplots:
18
für die 7b
Anne hat sich eine besonders interessante Lösung
ausgedacht: Beim Eintrag in die Listen ihres Taschenrechners fällt ihr auf, dass bei jedem Listenplatz der betreffende Schüler der 7b besser ist als
der auf dem gleichen Listenplatz befindliche aus
der 7a. Nur für den 29. Schüler der 7a findet sich
kein Vergleichspartner in der Parallelklasse. Anne
hat die Sprungweiten aller Schüler der 7a und die
aller Schüler aus der 7b addiert. Dabei stellt sie
fest, dass die gesamte Sprungweite aller 28 Schüler
der 7b nur um 1 cm kürzer ist als die der 29 Schüler
der 7a. Daraus folgert sie, dass die 7b nur
irgendeinen Schüler für den 29. Sprung nominieren
muss. Dieser Schüler muss noch nicht einmal
springen, er braucht nur einen kleinen Schritt zu
machen, um die Gesamtsprungweite der 7a zu
übertreffen. Daher ist für sie klar, dass im
Weitsprung die 7b besser als die 7a ist.
Annes Idee, die Sprungweiten zu addieren, kann
ich gut ausnutzen, um die beiden Aspekte zum
arithmetischen Mittelwert zu verdeutlichen:

Die Verteilung der Gesamtsprungweite auf 28
(bzw. für die 7a 29) gleich große Teile führt
zum arithmetischen Mittelwert und

Die Summe der Abweichungen aller
Sprungweiten vom arithmischen Mittelwert ist
Null.
Lernende müssen nicht nur die Gleichung zum Berechnen des arithmetischen Mittelwerts kennen und
anwenden können, sie müssen sie auch veranschaulichen und wesentliche Eigenschaften damit
verbinden können. Daher freue ich mich über jede
sich bietende Gelegenheit und nutze sie zur
Verankerung.
S = 3,80 m - 3,02 m = 0,78 m.
Nach diesem Kriterium wird man also Klasse 7a
als die ausgeglichenere der beiden Klassen
bezeichnen. Aber Lernende können unter
„ausgeglichen“ auch etwas anderes verstehen. In
Abschnitt 2 ist für sie Jan mit seinen Schätzungen
am ausgeglichensten, weil sich die Abweichungen
seiner Schätzungen (in etwa) ausgleichen. Wenn
also die Summe aller Abweichungen Null ergibt,
dann liegt in diesem anderen Sinne ideale Ausgeglichenheit vor.
Lösungsskizzen zu 3:
Zunächst muss man festlegen, ab welcher Sprungweite man von einer Spitzenleistung reden will.
Setzen wir hier zum Beispiel 3,50 m als eine solche
Grenze fest. In der Klasse 7a sind es 3 vom 29
Schülern, also rund 10 %, die mindestens 3,50 m
gesprungen sind, in der 7b sind es 9 von 28
Schülern, also rund 32 %. Sowohl absolut als auch
relativ sind es in der 7b mehr, sie hat also die
stärkere Spitze.
Lösungsskizzen zu 4:
Diese Frage ist eigentlich schon in Aufgabe 3 beantwortet worden. In Klasse 7a gibt es weniger
Schüler als in der 7b, die mindestens 3,50 m springen. Daher ist in Klasse 7a diese Sprungweite mehr
wert.
5. Leonardos Mensch
Mit der Federzeichnung von Leonardo da Vinci
„Die menschlichen Proportionen“ aus dem Jahre
1509 und dem zugehörigen Text
(vgl. zum
Beispiel bei Engel 2001) kann man die Phantasie
der Lernenden zu eigenen Tun und zu
selbständigen Untersuchungen gut anregen. In einer
9. Klasse stelle ich nach Einführung des CASTaschenrechners Leonardos Überlegungen zum
Menschen vor. Ein Satz fasziniert die Schülerinnen
und Schüler besonders: „Die Armspanne eines
Menschen ist äquivalent zu seiner Körpergröße.“
Das wollen sie näher untersuchen und dabei auch
ihren neuen Rechner mit einsetzen. Für 78
Messungen ergibt sich folgendes Bild:
Lösungsskizzen zu 2:
Lernende nennen hier meist als Kriterium für Ausgeglichenheit den Unterschied zwischen Maximum
und Minimum. Sie meinen damit eine Größe, die
Spannweite S heißt und als S = Maximum Minimum definiert wird. Für die 7a ist
S = 3,60 m - 2,92 m = 0,68 m,
19
Ich habe meine übrigen Lerngruppen (Klasse 7 und
den Leistungskurs in Jahrgang 12) mit einbezogen
und so Daten von insgesamt 78 Lernenden erfasst.
Auf der waagerechten Achse des Bildes wird die
Körpergröße der Lernenden und auf der dazu senkrechten Achse die zugehörige Armspannweite (beides in Meter gemessen) aufgetragen. Ein linearer
Trend ist der Punktwolke durchaus zu entnehmen.
Die Lernenden interpretieren „äquivalent“ mit
„gleich“, offenbar im Sinne von Leonardo.
Zunächst meinen sie, Leonardos Aussage müsse bei
jedem Menschen immer exakt zutreffen. Sie stören
sich an den Abweichungen von Körpergröße und
Armspannweite, auch wenn sie gering sind, und
argwöhnen, dass sie selber nicht oder nicht so ganz
Leonardos Vorstellungen von einem wohlproportionierten Menschen entsprechen. Aber haben zu
Leonardos Lebzeiten alle Menschen diesem Ideal
entsprochen? Nach einer intensiven Diskussion
formuliert die Lerngruppe als Ergebnis, Leonardos
Aussage als Modell zu nehmen, die etwas über
einen (gedachten) durchschnittlichen Menschen
aussagt, auch als Anleitung für Künstler gedacht,
die menschlichen Proportionen in Zeichnungen so
wiederzugeben, dass die Darstellung von Menschen
natürlich wirkt. Nun verstehen sie Leonardos
Aussage so: Die Armspannweite ist (in etwa)
gleich der Körpergröße, dabei sind mehr oder
weniger große Abweichungen nach oben und nach
unten natürlich und gleichen sich im Idealfall aus.
In der Lerngruppe wird auch eine andere
Interpretation geäußert: Die Armspannweite und
die Körpergröße sind proportional mit einem Proportionalitätsfaktor nahe bei 1.
Ich habe keine Regressionsrechnung durchführen
lassen. Die Lernenden haben eine Ursprungsgerade
nach Augenmaß in das Bild eingezeichnet und
deren Steigung bestimmt, wobei die Steigungen in
der Nähe von 1 liegen. Es herrscht Übereinstimmung darüber, dass der Graph durch den Ursprung
gehen muss. Einige Lernende gehen noch weiter,
haben eine Ursprungsgerade durch P( x  y ) gewählt und deren Gleichung bestimmt. Sie argumentieren, dass eine Gerade, bei der die Summe aller
Abweichungen Null ist, die Abweichungen sich
also insgesamt ausgleichen, durch P gehen muss.
Dies Ergebnis haben wir in der Diskussion, wie
Leonardos Behauptung zu verstehen ist, erhalten.
Da die Lernenden Steigungen erhalten, die fast 1
betragen, ist für sie klar, dass
Leonardos
Behauptung auch auf heutige Menschen angewandt
werden kann, allerdings nicht als Aussage, die für
jeden einzelnen Menschen exakt gilt, sondern als
ein Modell, das Prognosewerte liefert, um die die
tatsächlichen Werte schwanken.
Kein Schüler hat den Regressionsmodul des Rechners eingesetzt. In der Vorbereitung habe ich mir
schon Gedanken gemacht, wie die dabei entstehenden Gleichungen zu interpretieren sind, vor allem,
wie ein y-Achsenabschnitt ungleich Null zu
erklären und zu interpretieren ist. Die Gleichung
y = 0,97x + 0,0057 kann für die Daten der
7. Klasse gewonnen werden. Für die Körpergröße
wähle ich die Variable x und für die
Armspannweite die Variable y. Bei der Gleichung
für Klasse 7 können wir den y-Achsenabschnitt
noch als systematischen Fehler bei der Messung
der Armspannweite interpretieren, aber das macht
bei betragsmäßig größeren y-Achsenabschnitten
keinen Sinn mehr. Die Schülerinnen und Schüler
haben die Messungen sehr sorgfältig durchgeführt.
Einen systematischen Fehler von zum Beispiel 23
cm oder -17,5 cm hätten sie bereits bei der
Messung moniert und die Messung sofort wiederholt. Bei solchen Gleichungen können wir den Definitionsbereich auf Körpergrößen größer als 1,50
m einschränken und brauchen uns dann um die Interpretation
des
y-Achsenabschnitts
keine
Gedanken mehr zu machen.
Die Lernenden haben selbständig begonnen, eindimensional zu arbeiten, also nur die Körpergrößen
oder nur die Armspannen zu betrachten. Sie
wollten noch mehr Informationen aus den Daten
herausholen. Zu den drei Boxplots für die
Körpergrößen der Schülerinnen und Schüler, die
sie mit ihren Rechnern selbständig erstellt haben,
habe ich ihnen die Aufgabe gestellt, sich ein Bild
von den Größenverhältnissen in den drei Lerngruppen zu machen.
20
Konkret: Fertigt eine Zeichnung an, wie die Aufstellung der Schüler aussehen wird, wenn sie der
Größe nach geordnet sind.
Für die eigene Lerngruppe ist dies kein Problem,
man kann die Aufstellung ja konkret durchführen
und die dabei gemachten Erkenntnisse bei den
Zeichnungen der anderen Lerngruppen mit
einbeziehen.
Dass Lernende von Jahr zu Jahr größer werden und
auch von Jahrgang zu Jahrgang größer sind, ist eine
Erfahrungstatsache. Es verwundert uns nicht, dies
an den Boxplots zu erkennen. Aber gibt es keinen
Unterschied in den Größen und in der Größenverteilung mehr zwischen den Schülern des 9. und des
12. Jahrgangs? Die beiden Boxplots zwingen zum
genauen Hinschauen. Der etwas längere obere
Whisker und der größere Abstand von 3. Quartil
und Median beim Boxplot der 12. Klasse müssen
erkannt und entsprechend interpretiert werden.
Noch interessanter werden die Boxplots, wenn man
nach Geschlechtern trennt.
Gibt es nur bei den Jungen ein deutliches Größenwachstum? Ist es bei den Mädchen schon meist in
der 7. Klasse fast abgeschlossen? Man muss schon
genau hinschauen, um doch noch Unterschiede zu
entdecken. Interessant ist auch, wie Ausreisser in
der gesamten Klasse in den nach Geschlechtern getrennten
Teilgruppen
verschwinden
beziehungsweise neu hinzukommen. Wenn man die
Lerngruppen vor sich stehen sieht, ist dieser Effekt
nicht unvermutet und wird auch von den Lernenden
vorher so prognostiziert. Gibt es auch Boxplots
ohne Whiskers? Der Boxplot der Jungen im LK
ohne oberen Whisker provoziert diese Frage. Im
LK ist die Ursache schnell entdeckt. Hier ist der
Grund offensichtlich. In der 9. Klasse gebe ich
folgende Informationen als Arbeitsauftrag: Es sind
5 Schüler im LK, die folgende Körpergrößen
(jeweils in m) haben: 2,01; ...; 1,97; 1,91; 1,79.
Wie groß ist der zweitgrößte Junge im LK? Die Lösung lautet: 2,01 m. Nun ist klar, warum es keinen
oberen Whisker gibt. Bei diesem Beispiel ist noch
mehr deutlich geworden: Es macht keinen Sinn,
Boxplots bei weniger als 5 Daten zu zeichnen, und
auch nicht, Statistik mit so wenig Daten zu treiben.
„Schade, dass wir nicht die Entwicklung der gleichen Schüler von der 7. Klasse bis zum LK mit den
Boxplots dokumentieren,“ meinte Janina. Recht hat
sie, aber das wäre ein sehr reizvolles Vorhaben, für
das man einige Jahre warten muss, bis man die
Daten bereit hat. Im nächsten Schuljahr kommen
die 5. Klassen in Niedersachsen wieder zum Gymnasium. Vielleicht greift ein Leser oder eine
Leserin diesen Vorschlag auf und verfolgt die
Entwicklung von Schülern von der 5. Klasse bis
zum Abitur.
Andere Schüler haben die Differenz aus der Armspannweite und der Körpergröße ausgerechnet. Das
Streudiagramm mit allen 78 Daten zeigt, dass in der
Mehrzahl der Fälle diese Differenz negative Werte
annimmt. Die Lerngruppe meint, dass man dies
beim Streudiagramm deutlicher als in der
Datenliste sieht. Ich verzichte dennoch auf diesen
Graphen und stelle sofort die noch informativeren
Boxplots für die drei Klassen dar:
21
6. Abschlussbemerkungen
Nähern sich die Körpergröße und die
Armspannweite im Laufe der Jahre (in etwa)
einander an? Sollte man die Gültigkeit von
Leonardos Aussage vielleicht nur an erwachsenen
(im Sinne von ausgewachsenen) Menschen erproben? Gibt es Jahre, in denen das Breitenwachstum stärker als das Längenwachstum ist? All das
sind Fragen, die sich meine Schülerinnen und
Schüler beim Betrachten dieser Boxplots stellen.
Will man diesen Fragen weiter nachgehen, wird
man bei einigen von ihnen neue Erhebungen gezielt
durchführen müssen. Ich habe aus Zeitgründen
darauf verzichten müssen. Vielleicht regt dies eine
Leserin oder einen Leser zu eigenen Untersuchungen an und wir lesen hier den Bericht.
Noch interessanter sind die Boxplots für die Differenz aus der Armspannweite und der Körpergröße,
wenn man nach Geschlechtern trennt. Die Spannweite (Differenz zwischen Maximum und
Minimum in den Boxplots) wird im Laufe der Jahre
kleiner, der Median rückt in die Nähe von Null.
Aber die geschlechtsspezifischen Unterschiede in
meinen Lerngruppen sind nicht zu übersehen.
Man kann ein Projekt durchführen, bei dem man
zuerst jahrelang Daten sammeln muss, bevor die
Auswertung beginnen kann. Solch ein Projekt mit
überraschenden Ergebnissen wird beispielhaft in
Nordmeier[1989] dargestellt. Man kann auch von
seinen Schülerinnen und Schülern einen
umfangreichen Datensatz zusammentragen lassen.
Ein solches projektartiges Vorhaben wird zum Beispiel in Wirths[2002] beschrieben. In diesem Beitrag möchte ich andere Vorgehensweisen vorstellen: Daten werden von den Lernenden selbst
schnell erstellt, so dass die Auswertung noch in
derselben Stunde zu ersten Ergebnissen führt. Nach
der Datensammlung stellen Schülerinnen und
Schüler selbst eine Frage, die sie geklärt wissen
wollen, zu deren Beantwortung sie eine eigene
Strategie entwickeln müssen. Man kann vielfältige
Anässe dafür schaffen oder nutzen. Dies ist das
Anliegen des ersten Beispiels. Wie man Schülerimpulse oder -fragen aufgreifen, Daten und
Informationen sammeln, dabei auch vorgegebene
Daten, wo immer man sie findet, integrieren und
die dabei aufkommenden Fragen und Irritationen
klären kann, wird im zweiten Beispiel vorgestellt.
Mit gut gewählten Leitfragen, die Lernende vor
allem in Wettbewerbssituationen gern selbst entwickeln, kann ebenfalls gut in statistisches Denken
eingeführt werden. Dies soll im dritten Beispiel
verdeutlicht werden. Wie man Anregungen aus der
Geschichte in lebendigen Unterricht mit interessanten Ergebnissen integrieren kann, soll das vierte
Beispiel zeigen.
Diese Beispiele müssen nicht der Reihe nach abgearbeitet werden. Wenn vom kommenden Schuljahr
an in Niedersachsen wieder Unterricht am
Gymnasium von der 5. Klasse an möglich wird,
dann sollte man diese Beispiele in den Unterricht
der 5. bis 8. Klasse so integrieren, dass in jedem
Schuljahr Statistik betrieben wird, und dass in
jedem Schuljahr der Schatz an StatistikErfahrungen und an Fingerspitzengefühl im
Umgang mit Daten vergrößert wird.
Wichtig ist mir, dass Schülerinnen und Schüler von
Anfang an in die Problemstellung und -findung mit
einbezogen werden, Gelegenheit erhalten, selbst
Daten zu sammeln oder zu produzieren, eigene
Fragen zu stellen, die sie beantwortet wissen
wollen, dabei Erfahrungen sammeln, Fingerspitzengefühl im Umgang mit Daten entwickeln
und auch Vorurteile und Hypothesen auf den
Prüfstand stellen können.
22
Wenn man das Erstellen von Daten Lernenden
überlässt, kann es leider auch vorkommen, dass mit
solch selbsterstellten Daten die vom Lehrenden
gesetzten Lernziele nicht oder nur schwer zu
erreichen sind. Damit müssen Lehrende rechnen
und dürfen nicht überrascht sein, wenn dieser Fall
eintritt. Häufig entsteht jedoch Material, das zu
vielfältigen Fragen und Interpretationen anregt.
Dieses Material sollten Lehrende gezielt sammeln,
um es dann zu einem späteren Zeitpunkt in den Unterricht einbringen zu können, sobald sie dies für
erforderlich halten.
Schülerinnen und Schüler sollen im Statistikunterricht lernen, mit den unterschiedlichen Darstellungsformen umzugehen und selbständig zu entscheiden, ob sie bereits anhand der vollständigen
Datentabelle Aussagen begründen können oder andere Darstellungsformen wie zum Beispiel StengelBlatt-Diagramme oder Boxplots dazu benötigen.
Ich habe in meinen Beispielen an einigen Stellen
bewußt mehr Möglichkeiten aufgezeigt als
unbedingt zur Beantwortung der aufgeworfenen
Fragen erforderlich sind, um die Vielfalt an
Möglichkeiten zu verdeutlichen. Auch in meinem
Unterricht benötige ich diese Vielfalt; denn ich
beobachte, wie unterschiedlich Lernende reagieren
und argumentieren. Der eine beruft sich bei seinen
Ausführungen auf die - ggfs. um zusätzlich
berechnete Größen erweiterte - Datentabelle,
andere
wiederum
benötigen
verschiedene
graphische Darstellungen zur Unterstützung ihrer
Argumentation. Diese meinen Unterricht bereichernde Vielfalt möchte ich unterstützen und weiterentwickeln, und nicht durch einseitige Festlegung oder frühzeitige Einengung auf nur eine Möglichkeit verhindern.
Literatur
Engel, J. (2001): Datenorientierte Mathematik und
beziehungshaltige Zugänge zur Statistik:
Konzepte und Beispiele. In: Borovcnik,
M./Engel, J./ Wickmann, D., Anregungen zum
Stochastikunterricht. Franzbecker, Hildesheim
2001
Nordmeier, G. (1989): Erstfrühling und Aprilwetter Projekte in der explorativen Datenanalyse. Stochastik in der Schule Heft 3/1989, S. 21 - 42
Wirths, H. (2002): Sind deutsche Autos anders als
ausländische? StoiS 1/2002, S. 16 - 23
Anschrift des Verfassers
Helmut Wirths
Cäcilienschule Oldenburg
Haarenufer 11
26122 Oldenburg
[email protected]
23
Vernetzungen zwischen Vektorgeometrie und Beschreibender
Statistik
JÖRG MEYER, HAMELN
Zusammenfassung: In der Beschreibenden
Statistik kommen häufig Quadratsummen vor.
Deutet man diese als Skalarprodukte, so lassen
sich manche Aussagen über Mittelwerte, Varianzen
oder
über
Regressionskoeffizienten
in
durchsichtiger Weise vektorgeometrisch deuten
und beweisen. Auch zur Matrizenrechnung wird ein
Zusammenhang hergestellt. Behandelt werden die
Themenkomplexe Minimalität des arithmetischen
Mittels,
Regressionsgeraden
und
Regressionsparabeln. Auch zur Lagebeziehung von
arithmetischem Mittel und Median wird ein
Zusammenhang hergestellt.
1. Einleitung
Anders formuliert: Die Aufgabe
„Bestimme c so, dass
n
  c  di 
2
minimal ist“
i 1
wird durch c   gelöst.
Dies lässt sich auch vektorgeometrisch beweisen!
Dazu führen wir zwei n-dimensionale Vektoren ein,
 d1 
 
und zwar den Datenvektor D   ...  sowie den
d 
 n
1
 
Einsenvektor E   ...  . Mit dem Standard-Skalar1
 
n
In
den
neuen
Bundes-Einheitlichen
Prüfungsanforderungen im Fach Mathematik steht:
„Die Prüfungsaufgaben im Abitur erfordern einen
Unterricht, der in den drei Sachgebieten (Analysis,
Lineare Algebra / Analytische Geometrie und
Stochastik)
den
Aufbau
adäquater
Grundvorstellungen der zentralen Begriffe und
Methoden als Schwerpunkt hat [...].“
Das ist neu! Und das wird nur gelingen, wenn man
die drei Gebiete vielfältig miteinander vernetzt.
Hier geht es um Vernetzungen zwischen der
Beschreibenden Statistik und der Vektorgeometrie.
Zur Notation: Im Folgenden werden Punkte mit
ihren zugehörigen Ortsvektoren identifiziert.
produkt X  Y   x i  yi schreibt sich die Aufgabe
i 1
folgendermaßen: „Bestimme c so, dass der Vektor
 c  d1 


 ...   c  E  D minimale Länge hat“.
c  d 
n

Die (geometrische) Lösung ist offensichtlich: Man
muss nur D auf E senkrecht projizieren (Abb. 1).
2. Zur Minimalitätseigenschaft
des arithmetischen Mittels
Es seien d1 , d 2 , ...,d n irgendwelche numerischen
d  d  ...  d n
Daten
und
deren
: 1 2
n
arithmetisches Mittel. Die Minimalitätseigenschaft
des arithmetischen Mittels lautet so:
n
Für alle c ist
n
    di     c  di  .
i 1
2
2
Abb. 1
Die Länge von c  E  D ist minimal, wenn
c  E  D auf E senkrecht steht, wenn also
DE
c  E  E  D  E und deswegen c  2   gilt.
E
n
d1 ... d n
i 1
Stochastik in der Schule 24 (2004) Heft 1, S. 24 – 29
24
Die
E D 
Länge
n
    di 
2
des
Forderung an die zu findende Gerade besteht darin,
dass
n
i 1
Abweichungsvektors
ist
Wesentlichen
die
Standardabweichung.
Die bei der Berechnung der empirischen Varianz
häufig verwendete Formel
n
n
i 1
i 1
2
    di    di2  n  2 .
ist nur der Satz des Pythagoras in der Form
   E  D 2  D2     E 2 .
Eine Analogisierung dieser Betrachtungen in
Richtung Verknüpfung zwischen Vektorgeometrie
und Wahrscheinlichkeitsrechnung findet sich bei
Scheid, H. (1986): Stochastik in der Kollegstufe.
BI: Mannheim.
3. Der Regressionskoeffizient
und Projektionen
x 
Gegeben sind n Datenpaare  i  ( i  1, ..., n ).
 yi 
Gesucht ist diejenige Gerade („Ausgleichs-“ oder
„Regressionsgerade“)
mit
der
Gleichung
y  a  x  b , die die Daten möglichst „gut“
annähert. Die y-Werte sind möglicherweise
messfehlerbehaftet, die x-Werte nicht.
  a  x i  b  yi 
2
minimal
i 1
wird. Abweichend von Abschnitt 1 kürzen wir die
n
arithmetischen Mittel hier als x 
 xi
i 1
n
n
und y 
 yi
i 1
n
ab.
Die erste Forderung
n
  a  x i  b  yi   0
i 1
schreibt sich dann als
ax b  y ;
die gesuchte Gerade geht somit durch den
Schwerpunkt. (Das ist auch der Fall, wenn nicht die
Summe der vertikalen Abstände, sondern die
Summe der zur Ausgleichsgerade senkrechten
Abstände - in Abb. 3 durch Einfachlinien
gekennzeichnet - verschwinden soll.)
Abb. 3
Abb. 2
Daher
liegt
eine
Koordinatenverschiebung
u:  x  x; v:  y  y nahe; sie führt zu
Was heißt „gut“? Sicherlich ist es sinnvoll zu
fordern, dass die Summe der vertikalen Abstände
(in Abb. 2 durch Doppellinien gekennzeichnet)
verschwindet, d. h. dass
 ui   xi  x 
,
   
 vi   yi  y 
n
  a  x i  b  yi   0
und die Regressionsgerade bekommt die einfache
Gleichung v  a  u .
i 1
ist. Damit ist aber die Regressionsgerade noch
nicht eindeutig bestimmt. Eine weitere (fruchtbare)
25
Natürlich ist u  v  0 , diese Gleichungen lassen
 u1 
 v1 
1
 
 
 
sich mit U   ...  , V   ...  und E   ...  als
1
u 
v 
 
 n
 n
Orthogonalitätsrelationen
UE  VE  0
deuten.
Die zweite Forderung
n
  vi  a  u i 
(OR)
2
minimal
i 1
bedeutet: Wähle a so, dass a  U  V möglichst
kurz ist. Man bekommt dieses a, wenn man V auf U
senkrecht projiziert (Abb. 4).
n
  vi   a  u i  b  
2
minimal .
i 1
Wir haben dann das Problem:
Bestimme a und b so, dass
 u1 
 1   v1 
 
   
a   ...   b   ...    ...   a  U  b  E  V
u 
1 v 
 n
   n
möglichst kurz ist!
U und E spannen eine Ebene auf. Gesucht sind
dann a und b so, dass der Abstand zwischen
a  U  b  E und V minimal ist.
Das erreicht man, wenn man den Vektor V auf die
von U und E aufgespannte Ebene senkrecht
projiziert (Abb. 5).
Abb. 4
Es ist dann a so zu bestimmen, dass
 V  a  U  U  0
ist, was auf a 
UV
2
führt. Bekanntlich heißt a
U
Regressionskoeffizient.
An dieser Stelle sollte man
wie gut die Datenpunkte
beschrieben werden.
Wenn alle Daten genau auf
ist V  a  U . Genau dann ist
der Frage nachgehen,
durch eine Gerade
einer Geraden liegen,
cos(U, V)  1 .
Auf der anderen Seite hat man die maximale
Abweichung von einer Geradenform, falls U und V
zueinander senkrecht stehen. Genau dann ist
cos(U, V)  0 .
Daher ist der Korrelationskoeffizient
UV
cos(U, V) 
ein gutes Maß dafür, wie gut
UV
die Datenpunkte durch eine Gerade beschrieben
werden können.
Nebenbei: Die vorgängige Bestimmung von b  0
ist sachlich überflüssig (allerdings didaktisch
sinnvoll), es reicht die zweite Forderung
Abb. 5
Wie bestimmt man die Projektion? Es muss sein:
 a  U  b  E  V   U  0 und
a  U  b  E  V  E  0 .
Dies Gleichungssystem lässt sich besonders einfach
lösen, falls (E, U) eine Orthogonalbasis ist. Dies ist
UV
aber hier wegen (OR) der Fall. Dann ist a 
UU
EV
und b 
 0.
EE
4. Der Regressionskoeffizient der
standardisierten Daten
Wir hatten die Daten
 xi 
 
 yi 
zentralisiert zu
 ui   xi  x 
 . Nun ist es eine sinnvolle Idee, die
   
 vi   yi  y 
26
Daten auch zu normieren zu S 
T
U

U
 U2

 0
und
V
  . Dabei ist natürlich   0 .
V
Vom Standpunkt der Vektorgeometrie aus ist   1
naheliegend, vom Standpunkt der Stochastik ist es
  n oder   n  1 . Alsdann ist S  T   .
Berechnet man für diese normierten Daten den
Regressionskoeffizienten, so bekommt man
U
V


V
ST U
UV
a 2 

 cos(U, V) .
U
U
S

 U  V
U
U
Für (irgendwie) normierte Daten stimmen also
Regressions- und Korrelationskoeffizient überein.
5. Der Regressionskoeffizient
und Matrizen
Das Problem bei der Regressionsgerade war:
Bestimme a und b so, dass
 u1 
1
a
 
 
a   ...   b   ...   a  U  b  E   U, E    
b
u 
1
 :M
 n
 
 u1 1 
a

 a
  ... ...      M   
 b
u
 b
 n 1
0 a  UV
   

n   b   0 
und hat die Lösung a 
UV
U2
und b  0 .
6. Der Zusammenhang zwischen
arithmetischem Mittel, Median
und Standardabweichung
Es seien d1 , d 2 , ...,d n wie in Abschnitt 1
irgendwelche
numerischen
Daten
und
d1  d 2  ...  d n
deren arithmetisches Mittel,
:
n
n
  di   
2
i 1

deren
n
sowie  deren Median.
Standardabweichung
Dann gilt: Der Abstand der beiden Mittel  und 
ist durch  beschränkt, d. h. es gilt:
   .
Wie kann man das beweisen? Wir fangen mit dem
linken Term an. Nach der Dreiecksungleichung für
Beträge gilt
  
1 n
1 n
   di       di  
n i1
n i1
M
und aufgrund der Minimalitätseigenschaft des
Medians ist
 v1 
 
sich möglichst wenig von  ...   V unterscheidet.
v 
 n
1 n
1 n
  di      di   .
n i 1
n i 1
Zu lösen wäre also das überbestimmte System
a
M    V .
Hier
liegt
ein
anderer
b
Repräsentationswechsel als bei den Projektionen
vor.
Man multipliziert auf beiden Seiten mit der
Mt
transponierten
Matrix
und
erhält
a
M t  M     M t  V . Hier ist M t  M eine
b
quadratische und symmetrische Matrix, und dies
Gleichungssystem ist lösbar! Man erhält
 U2 0 
UV
Mt  M  
Mt  V  
.
 0 n  und
 0 


Das Gleichungssystem lautet also
Wenn nun noch
n
  di   
n
1
  di   
n i 1
i 1
n
2

gelten würde, hätte man die Behauptung bewiesen.
Schreibt man, um die Struktur des zu Beweisenden
klarer zu sehen, z i für di   , so muss
n
 zi
i 1
n
n

 zi2
i 1
n
bzw.
2
n
 n

2
  zi   n   zi
i 1
 i1 
(U)
27
gelten. Nun kann man in der rechten Seite von (U)
 z1 
 
ein Skalarprodukt zu erkennen. Mit Z   ...  und
z 
 n
1
 
E   ... 
1
 
sowie
dem
Standard-Skalarprodukt
n
X  Y   x i  yi ist n  E  E , und (U) schreibt
i 1
 Z  E 2  E2  Z2 ; das ist
2
wegen  Z  E   E 2  Z2  cos2  E, Z  .
sich als
Vernetzungen
zwischen
Vektorgeometrie
lohnen
Repräsentationswechsel
aber richtig
Stochastik
sich
also!
und
Der
Quadratsumme  Skalarprodukt
ist häufig fruchtbar, wie an den Beispielen wohl
deutlich geworden ist.
     
hat.
7. Zur quadratischen Regression
Die Methoden von Abschnitt 2 lassen sich
fruchtbar
machen
zur
Erläuterung
der
quadratischen Regression. Wieder haben wir n
x 
Datenpaare  i  ( i  1, ..., n ), und gesucht ist
 yi 
diejenige Parabel, die die Daten möglichst „gut“
annähert. Wie im Fall der linearen Regression wird
es sich als vorteilhaft erweisen, wenn man eine
Schwerpunktstranslation
vornimmt
und
zu
 ui   xi  x 
 übergeht. Es sind dann a, b und c
   
 vi   yi  y 
so zu bestimmen, dass die v i möglichst dicht bei
den jeweiligen Werten für a  u i2  b  u i  c liegen.
Mit
 u12 
 u1 
 v1 
1
 
 
 
 
2
u2 
v2 
1
 u2 


U
, Q:    , V 
und E   
 ... 



...
... 
 ... 
 
 
 
 2 
1
 un 
 vn 
 un 
Übrigens: Analysiert man den Beweis zu
     , so stellt man fest, dass sich genauere
Aussagen machen lassen:
Die Dreiecksungleichung für Beträge liefert
1 n
1 n
       di       di   .
n i1
n i1
Die rechte Seite ist das zum Median gehörige
n
: 
Streuungsmaß

di  
i 1
n
absolute Abweichung. Damit ist
,
die
mittlere
    .
Aufgrund der Minimalitätseigenschaft des Medians
gilt
n


i 1
n
di  

n

i 1
di  
Nun ist wie oben
n

i 1
n
di  
n

  di   
i 1
n
2
,
so dass man insgesamt die Ungleichung
dicht
bei
Hier
ist
der
Anlass,
geometrische
Grundvorstellungen
auf
den
nicht
mehr
vorstellbaren
vierdimensionalen
Raum
zu
erweitern:
 Wenn a  U  V möglichst kurz sein soll, muss
man V auf die durch den Richtungsvektor U
aufgespannte Ursprungsgerade projizieren
(Abschnitt 1).
 Wenn a  U  b  E  V möglichst kurz sein soll,
muss man V auf die durch die
Richtungsvektoren U und E aufgespannte
Ursprungsebene projizieren (Abschnitt 2).

.
n
heißt das: V soll möglichst
a  Q  b  U  c  E liegen.
Wenn a  Q  b  U  c  E  V möglichst kurz
sein soll, so sollte man analog V auf
denjenigen
dreidimensionalen
Raum
projizieren, der durch den Ursprung geht und
durch die drei Richtungsvektoren Q, U und E
aufgespannt wird.
Analog zu den Abschnitten 1 und 2 führt das auf
die drei Bedingungen
a  Q  b  U  c  E  V  Q  0
a  Q  b  U  c  E  V  U  0
28
a  Q  b  U  c  E  V  E  0 .
(Man gelangt übrigens zu den gleichen Termen,

i 1
n
wenn man  :   a  u i2  b  u i  c  vi

2
nach a,
b und nach c ableitet, dieser Weg hätte natürlich
auch schon früher offen gestanden.)
Aufrund der Orthogonalitätsrelationen (OR) und
wegen
schreibt
sich
das
QE  U U
Gleichungssystem einfacher als
a QQ  bUQ  cUU  VQ
a QU  bUU
 UV
aUU
 cEE 
0
Das Gleichungssystem wird noch etwas einfacher,
wenn man die x-Werte als äquidistant annimmt,
wenn also x i 1  x i  u i 1  u i von i unabhängig
ist. Unter dieser Voraussetzung ist nämlich
U  Q  0 , und man bekommt das recht
übersichtliche System
a QQ
 cUU  VQ
bUU
 UV
aUU
 cEE 
0
 1  0 
Beispiel: Gegeben seien die 4 Punkte   ,   ,
 2  1
1
 2
  und   , für die die Ausgleichsparabel
 3
 3
1
9
und y  ist
2
4
9/ 4
 1/ 4 




1/ 4 
5 / 4 
Q
und V  
.
 1/ 4 
 3/ 4 




9/ 4
 3/ 4 
Abb. 6
Die Vorgehensweise überträgt sich auf Polynome
höheren Grades.
Bei der Parabelregression kann es natürlich
passieren, dass der führende Koeffizient a
verschwindet. Man sieht am Gleichungssystem,
dass das genau dann der Fall ist, wenn Q auf V
senkrecht steht (wie es auch zu erwarten ist).
Alsdann ist natürlich auch c  0 .
 1 
1
 
 
0
2

Abb. 7 zeigt das Beispiel X 
, Y    . Man
1
 2
 
 
2
 3
muss Y nur an einer Stelle geringfügig verändern,
um aus der Geraden eine nach oben oder eine nach
unten geöffnete Parabel zu erzeugen.
gesucht ist. Wegen x 
 3/ 2 


1/ 2 
U
,
 1/ 2 


 3/ 2 
Das Gleichungssystem hat die Lösung
1
1
5
, b , c ;
4
2
16
die Ausgleichsparabel hat somit die Gleichung
Abb. 7
a
v
u2 u 5
  ; Abb. 6 zeigt die Situation.
4 2 16
Anschrift des Verfassers
Jörg Meyer
Schäfertrift 16
31789 Hameln
[email protected]
29
Rezensionen
Gerd Gigerenzer: Das Einmaleins der Skepsis.
Berlin: Berlin Verlag, 2002 (gebunden); Berlin: Btv, 2004 (broschiert)
REZENSION VON GERHARD KÖNIG
Medizinische Testergebnisse enthalten für die
meisten Patienten unumstößliche Wahrheiten. Ob
beim HIV-Test, bei der Mammographie oder bei
der Früherkennung von Prostata-Krebs: Wer käme
auf die Idee, das Urteil des Arztes anzuzweifeln?
Dabei gibt es erwiesenermaßen Fehlurteile und
trügerische Sicherheiten - mit oft gravierenden
Folgen für die Betroffenen, Folgen, die sich nach
Aussage des renommierten Psychologen Gerd
Gigerenzer vermeiden ließen.“
So führt der Klappentext in das über 400 Seiten
starke Buch ein, dass den Lesern die Illusion der
Gewissheit bewusst machen will. Gigerenzer
konstatiert nämlich für die westlichen Kulturkreise
ein elementares Bedürfnis nach absoluten
Wahrheiten.
Als
Glaube
an
eindeutige
Gewissheiten bestimmt dieses Bedürfnis die Praxis
von Experten - und mehr noch die Erwartung der
Laien an die moderne Technologie. Ein zweites
Ziel des Buches ist es, dem Leser Methoden
anzubieten, mit denen er Risiken verstehen und
diese anderen verständlich mitteilen kann.
Gemäß dem Untertitel des Buches „Über den
richtigen Umgang mit Zahlen und Risiken“ zeigt
der Autor konkret an zahlreichen Beispielen, dass
man im Umgang mit Zahlen, vor allem mit
Prozenten
und
Wahrscheinlichkeiten,
zu
schnellgläubig ist. Anhand der detailliert
ausgebreiteten Fallbeispiele leuchtet das jedem
Leser ein. Dabei hat Gigerenzer zwei
Anwendungsschwerpunkte: Gesundheit / Medizin
und Straftaten / Kriminalität. Hauptsächlich die
Medizin hat es ihm angetan und dabei die
Mammographie,
die
er
heftig bekämpft
(„Mammographie-Illusion“) und die deswegen zu
ausführlich behandelt wird. Allein die ersten 160
von 330 Seiten befassen sich in endlosen
Variationen fast nur mit diesem Thema.
Wir wollen daher ein anderes Beispiel, das
Gigerenzer in seinem Buch erläutert, herausgreifen:
Die statistische Zuverlässigkeit von AIDS-Tests.
Diese Problematik wurde zudem auch schon in
Stochastik in der Schule 24 (2004) Heft 1, S. 30, 31
vielen
Artikeln
mathematikdidaktischer
Zeitschriften behandelt. Einer seiner Studenten
stellte sich in über 20 Beratungsstellen in
verschiedenen Städten Deutschlands vor und
fragte, was ein positiver Test in seinem Fall keinerlei Risikofaktoren - bedeuten würde.
Fast alle Berater sagten ihm voller Überzeugung,
die Möglichkeit eines Irrtums läge nahe bei Null,
weil der Test zu 99,9 Prozent sicher sei. Die
Angabe zur Testsicherheit ist richtig, aber die
Schlussfolgerung daraus ist falsch: In Wirklichkeit
ist sogar jede zweite positive Diagnose bei
Menschen aus keiner Risikogruppe "falschpositiv". Solche Probleme gehören zu den
Standardproblemen des Bayes-Theorem, dass ganz
selten richtig verstanden wird. Der positive
Vorhersagewert eines medizinischen Tests hängt
nicht nur von seiner Güte, d.h. Sensitivität bzw.
Spezifität, sondern auch wesentlich vom
Vorhandensein der betreffenden Krankheit in der
Bevölkerung ab, der sog. Prävalenz. Je geringer die
Wahrscheinlichkeit z.B. für eine HIV-Infektion in
der Bevölkerung ist - sprich, je weniger der Fall
einer Risikogruppe vorliegt -, desto genauer muss
getestet werden. Aber bei seltenen Krankheiten
können Tests mit je z.B. 99,9% Spezifität und
Sensitivität falsch-positive Werte von über 50%
erzeugen. Schlussfolgerung von Arthur Engel bei
der Besprechung eines ähnlichen Problems: „Bei
seltenen Ereignissen sind die meisten Alarme
falsche Alarme.“
Die Probleme, die dadurch entstehen, dass
frau/man positiv getestet wurde, aber mit größerer
Wahrscheinlichkeit gar nicht infiziert ist oder
Krebs hat, werden unter verschiedenen Aspekten,
medizinisch, psychisch und gesellschaftspolitisch,
diskutiert. Der Autor legt auch großen Wert auf
eine anschauliche Erklärung des Phänomens hoher
falsch positiver Raten bei seltenen Krankheiten.
Dazu geht er als Folge der Ergebnisse aus seinen
empirischen Untersuchungen davon aus, dass es
anhand der natürlichen Häufigkeiten leichter ist,
richtig zu überlegen als unter Nutzung von
30
Wahrscheinlichkeiten. „Natürliche Häufigkeiten
erleichtern es uns, aus numerischen Informationen
die richtigen Schlussfolgerungen zu ziehen.“
Visualiert werden die Schlüsse und Überlegungen
durch zahlreiche Baumdiagramme.
Warum fördert es das Verständnis, wenn man die
Informationen nicht als Wahrscheinlichkeiten oder
Prozentsätze, sondern als natürliche Häufigkeiten
angibt? Das hat zwei Gründe. Zum einen ist die
Berechnung einfacher, denn die Darstellung
erledigt sie schon teilweise. Der zweite Grund liegt
nach Überzeugung des Psychologen Gigerenzer in
der Evolution unseres Gehirns und der Entwicklung
unseres Denkens: Unser Verstand ist eben an
natürliche Häufigkeiten angepasst.
Inzwischen verstehen wir sehr genau, warum das so
ist. Wenn man eine natürliche Häufigkeit in eine
bedingte Wahrscheinlichkeit umrechnet, entfernt
man dabei die Information über den Grundanteil
(man nimmt eine so genannte Normalisierung vor).
Der Vorteil dieser Normalisierung besteht darin,
dass die resultierenden Werte stets im Bereich
zwischen 0 und 1 liegen. Wenn man jedoch aus
Wahrscheinlichkeiten Schlüsse zieht (anstatt aus
natürlichen Häufigkeiten), dann muss man die
Grundanteile wieder hineinbringen, indem man die
Wahrscheinlichkeiten der Ereignisse mit den
jeweiligen Grundanteilen multipliziert. (S.74)
Mit Fehldiagnosen und trügerische Sicherheiten in
der Medizin räumt der Autor also gründlich auf.
Nicht
nur
aus
den
ärztlichen
Untersuchungszimmern,
sondern
auch
aus
Gerichtssälen (Sachverständige im Gerichtssaal)
und Regierungsgremien berichtet er von
schwerwiegenden Fehleinschätzungen, die alle in
einem Mangel an statistischem Verständnis
gründen.
Er macht auf versteckte Denkfallen aufmerksam
und ermuntert zur Überprüfung von Zahlen der
(vermeintlichen) Experten.
Schließlich gibt es noch ein Kapitel „Amüsante
Aufgaben“, in dem der Autor den Leser einlädt, die
reale Welt zu verlassen und in die Welt der Spiele
und der Kopfnüsse einzutreten.
Didaktisch sehr gut schildert Gigerenzer das
Monty-Hall-Problem, auch als Drei-KastenProblem, Gefangenenproblem oder Drei-TürenProblem bekannt.
Ein Glossar mit Erklärungen der wichtigsten im
Buch verwendeten Termini sowie ein ausführliches
Literaturverzeichnis
mit
Nachweisen
der
behandelten Beispielsfälle runden das Buch ab.
Gigerenzer hat bei der Lektüre nicht den
Fachmann, Mathematiker oder sogar speziell
Stochastiker, ins Visier genommen, dazu ist
manches zu ausführlich und für den Wissenden zu
langatmig dargestellt. Es ist eher als Pflichtlektüre
für alle Mediziner, Juristen und Politiker und alle,
die mit Statistiken und Risiken (Börse!) umzugehen
haben gedacht. Auch die Kultusbürokratie wurde
nicht vergessen: „Unsere Ergebnisse mögen alle
diejenigen ermutigen, die Lehrpläne für die
Oberstufe oder für Studienanfänger entwickeln“ (S.
328).
Aber auch der Fachmann liest das eine oder andere
Kapitel mit Gewinn. Z.B. das Kapitel 10 „Der
genetische Fingerabdruck“ in dem der Autor zeigt,
dass der DNA-Vergleich nicht alle Ungewissheiten
beseitigt. Wie jedes neuartige Verfahren verringert
der genetische Fingerabdruck nicht nur alte
Ungewissheiten, etwa die über die Vaterschaft,
sondern bringt auch neue Ungewissheiten mit sich.
Oder kennen Sie den Kategorie-Effekt (S.265ff),
der immer dann auftritt, wenn eine bestimmte
Ungewissheit vorliegt, zum Beispiel wenn jemand
nur eingeschränktes Wissen hat, aber trotzdem ein
Verhalten beurteilen oder vorhersagen soll.
Statistik ist vor allem ein unverzichtbares
Instrument zur gesellschaftlichen Information und
zur Entscheidungsfindung in Politik, Wirtschaft
und für die Bürger selbst. Statistische Daten stellen
eine wichtige Grundlage dar, um Probleme zu
analysieren und darauf aufbauend fundierte
Lösungen zu entwickeln. Eben so wie die Fähigkeit
zu lesen und Texte zu verstehen für jeden Bürger
von höchster Bedeutung im Leben ist, so ist es von
ähnlich hoher Bedeutung, Daten und Zahlen zu
verstehen. Dazu will das Buch beitragen. Es zeigt
konkrete und frappierend einfache Möglichkeiten
auf, wie sich das statistische Analphabetentum in
unserer
so
genannten
Wissensgesellschaft
überwinden lässt. Verständlich und kurzweilig
unterbreitet Gigerenzer Vorschläge, wie der
Einzelne sein Verständnis von Risiken und
Wahrscheinlichkeiten verbessern kann, um letztlich
den unvermeidlichen Ungewissheiten im Leben
souveräner und gelassener zu begegnen.
Zum Schluss zwei Literaturhinweise zum Thema in
didaktischen Fachzeitschriften:
Krauss, Stefan: Wie man das Verständnis von
Wahrscheinlichkeiten verbessern kann: Das
'Häufigkeitskonzept'. In: Stochastik in der
Schule. (2003) v. 23(1) S. 2-9
31
Wassner, Christoph; Krauss, Stefan, Martignon,
Laura: Muss der Satz von Bayes schwer
verständlich sein? In: PM Praxis der
Mathematik in der Schule. Sekundarstufen 1
und 2. (Feb.2002) v. 44(1) S. 12-16
Gerhard König
32
Bibliographische Rundschau
GERHARD KÖNIG
G. Fölsch: Welche Farbe hat mein Hut. In: PM,
Praxis der Mathematik v.45(1.Dezember 2003)6; S.
289-292
Drei Spieler, die die rote oder blaue Hutfarbe
jeweils der beiden anderen sehen, aber nicht die
eigene, sollen diese erraten. Wird dabei eine
bestimmte Strategie angewandt, die mit dem
dreimaligen Werfen einer Münze zusammenhängt,
so
ergibt
sich
eine
verblüffend
hohe
Gewinnwahrscheinlichkeit für die Gruppe. Ist
dieses Spiel wesensverwandt mit der klassischen
Denksportaufgabe, in der Indianer drei Weiße je an
einen roten oder blauen Pfahl gebunden haben?
Wolfgang Härdle; Bernd Rönz: Statistik
Wissenschaftliche Datenanalyse leicht gemacht.
Ein interaktives Tool zur Einführung in die Welt
der Statistik. Berlin: Multimedia Hochschulservice,
2003
Die interaktiv konzipierte CD-ROM bietet ein
neuartiges Tool zur Einführung in die Welt der
Statistik. In zwölf Kapiteln werden alle klassischen
Teilgebiete der deskriptiven und induktiven
Statistik
behandelt.
Durch eine Vielfalt an Beispielen und interaktiven
Recheneinheiten wird die Materie leichter
erfassbar. Multiple-Choice-Fragen ermöglichen
eine Überprüfung des gelernten Stoffes. Besonders
geeignet für Studierende der Wirtschafts-, Naturund Ingenieurwissenschaften.
Jacobs, Konrad; Jungnickel, Dieter: Einführung in
die Kombinatorik. Berlin: de Gruyter, 2004.
Ziel dieser vollständig überarbeiteten und
erweiterten Neuauflage ist es, eine weitgehend
elementare Einführung in ausgewählte Teile der
Kombinatorik zu geben. Dabei wird stets versucht,
nicht nur die Grundlagen darzustellen, sondern
auch in jedem Kapitel exemplarisch einige tiefer
liegende Resultate vollständig zu beweisen. Einige
Highlights sind: 1. projektive Ebenen und Räume,
samt des Freundschaftstheorems, 2. Anwendungen
in der Kryptographie, Authentikation von
Nachrichten, Zugangskontrolle zu geheimen
Informationen, 3. Heiratssatz und verwandte Sätze,
etwa zu Flüsse auf Netzwerken, 4. der Satz vom
Diktator,
5.
einige
Perlen
aus
der
Codierungstheorie,
inklusive
konkreter
Anwendungen etwa bei Prüfziffersystemen, 6. der
klassische Satz von Ramsey und verwandte
Ergebnisse, 7. Partitionen und Abzählen, etwa das
klassische Menage-Problem, 8. Endliche Geometrie
und Graphentheorie.
Katja Krüger: Ehrliche Antworten auf indiskrete
Fragen – Anonymisierung von Umfragen mit der
Randomized Response Technik . In: Materialien für
einen realitätsbezogenen Mathematikunterricht,
Band 8, herausgegeben von Hans-Wolfgang Henn
und Katja Maaß. Hildesheim, Berlin: Franzbecker,
2004, S. 118-127
Das Thema „Umfragen“ ist Gegenstand des
Stochastikunterrichts und wird z. B. in der
Sekundarstufe II unter der Überschrift „Schätzen
unbekannter Wahrscheinlichkeiten“ behandelt. In
diesem Beitrag wird gezeigt, wie die
vergleichsweise
neue
Umfragetechnik
der
„Randomized Response“ im Unterricht behandelt
werden kann. Einen Einstieg ins Thema bieten die
Ergebnisse einer aktuellen Online-Umfrage zum
Thema Steuerhinterziehung. Bei der Analyse dieses
Beispiels werden grundlegende Konzepte der
Wahrscheinlichkeitsrechnung wieder aufgegriffen
und miteinander verknüpft. Mit Hilfe eines
Baumdiagramms und der Pfadregeln wird die
Wahrscheinlichkeit
einer
„sensitiven“
Verhaltensweise
geschätzt.
Stichprobenverteilungen werden erzeugt, grafisch
dargestellt und miteinander verglichen, um zu
Aussagen über die Genauigkeit des Schätzwertes
zu kommen.
Jörg Meyer: Schulnahe Beweise zum zentralen
Grenzwertsatz. Hildesheim, Berlin: Franzbecker,
2004 (texte zur mathematischen forschung und
lehre 31)
In dieser Arbeit wird der Frage nachgegangen, ob
es schulnahe Begründungen für den zentralen
Grenzwertsatz der Stochastik gibt. Dabei ist vorab
zu klären: 1. Was soll unter "Begründung"
verstanden werden?, 2. Was bedeutet "schulnah"?,
3.
Von
welcher
Form
des
zentralen
Grenzwertsatzes (lokal/global, Spezialfall von de
Moivre/Laplace oder allgemeine Aussage von
Lindeberg/Feller) soll die Rede sein? Der Hauptteil
dieser Dissertation besteht in der Erläuterung und
Stochastik in der Schule 24 (2004) Heft 1, S. 32 – 34
33
didaktischen
Einordnung
unterschiedlicher
Beweise zum zentralen Grenzwertsatz.
Günter Nordmeier: Es wird wärmer. In:
mathematiklehren, Heft 120 (Oktober 2003), S. 2122, S.47-48
Treibhauseffekt und Kimaschutz gehen uns alle an.
Aus Klimareihen lassen sich mit einfacher
Mathematik
kurzfristige
und
mittelfristige
Klimaschwankungen und der langfristige Trend
herausarbeiten und die zugehörigen Werte gut
abschätzen
eine
Anregung
für
fächerübergreifende Probleme und experimentelle
und explorative Ansätze im Mathematikunterricht.
Unterrichtsprojekt zu Zeitreihen.
Vancso, Oedoen: Wie verstehen die Studenten die
bedingten Wahrscheinlichkeiten? In: Beiträge zum
Mathematikunterricht 2003. Vorträge GDM 2003 .
Hildesheim: Franzbecker. 2003.S. 633-636
Im Vortrag werden die Ergebnisse eines mit ca. 300
Teilnehmern in
Budapest durchgeführten
Experiments vorgestellt. Solche Probleme werden
durch
einen
Fragebogen
formuliert,
die
''theoretisch'' mit Bayes-Theorem beanwortet
werden sollen. Die Erfahrungen werden mit den
Ergebnissen anderer ähnlicher Experimente - z. B.
in Berlin - verglichen. Einige didaktische
Hypothesen werden untersucht, und eine
Empfehlung bezüglich verschiedener Lernprozesse
für den Schulunterricht gegeben. Danach wird die
Entwicklung
des
Wahrscheinlichkeitsbegriffs
anhand der gezeigten Probleme diskutiert, und
Folgerungen gezogen.
Peter Rasfeld: Einführung in beschreibende
Statistik mit den Techniken der Explorativen
Datenanalyse. In: Materialien für einen
realitätsbezogenen Mathematikunterricht, Band 8,
herausgegeben von Hans-Wolfgang Henn und
Katja Maaß. Hildesheim, Berlin: Franzbecker,
2004
Die Behandlung herkömmlicher Methoden und
Begriffe der beschreibenden Statistik wird für
Schülerinnen und Schüler der Sekundarstufe I i.a.
als sehr schwierig eingestuft. Oftmals „entartet“
der Statistikunterricht, sofern er überhaupt
stattfindet, in einer mehr oder weniger formalen
Berechnung von Kenngrößen, ohne dass diesen wie
auch den Interpretationen der Ergebnisse
gebührend Beachtung geschenkt wird. Im
vorliegenden Beitrag soll gezeigt werden, wie die
modernen Methoden der explorativen Datenanalyse
hier Verbesserungen bieten können.
Peter Rasfeld: Verbessert der Stochastikunterricht
intuitives stochastisches Denken? Ergebnisse zu
einer empirischen Studie. In: Journal für
Mathematikdidaktik Jahrgang 25(2004)1, S. 33-61
Der Bildungsinhalt der Stochastik ergibt sich nicht
nur, wie oftmals betont wird, aus ihrem
Anwendungscharakter, sondern auch aus der
Tatsache, dass Grundelemente der Stochastik
unserem Denken immanent sind. Im Alltag erfolgt
die
Einschätzung
des
Grades
einer
Wahrscheinlichkeit meist spontan und intuitiv. Es
gibt eine Reihe von heuristischen Strategien, derer
sich Personen in solchen Fällen bedienen, und die
zu krassen Fehleinschätzungen führen können. In
der im Artikel beschriebenen Untersuchung in elf
Klassen der Jahrgangsstufe 10 in NRW wird der
Frage nachgegangen, inwieweit Schüler durch die
verbindlich vorgegebenen Stochastikinhalte lernen,
solche intuitiv getroffenen Fehlurteile zu
vermeiden bzw. Intuitionen aufzubauen, die eine
angemessene
Beurteilung
stochastischer
Fragestellungen ermöglichen. Als Fazit ergab sich,
dass
eine
Verbesserung
des
intuitiven
Verständnisses stochastischer Problemstellungen
zwar stattfindet, aber nicht im erwünschten
Ausmaß. Vorschläge zur Verbesserung der
Situation werden kurz skizziert.
Hans J. Schmidt: Prof. Dr. Rainer Tsufall – Die
Würfel sind gefallen. Kopiervorlagen Mathematik
zur Wahrscheinlichkeitsrechnung. Köln: Aulis
Verlag Deubner, 2003
Handlungsorientierte Matrialien für die Schüler der
Sekundarstufe 1 sowie Demonstrationsmodelle für
die
Overheadprojektion,
anhand
derer
Zufallsversuche demonstriert und kommentiert
werden können. Inhalt: Zufallsversuche und ihre
Ausfälle,
Wahrscheinlichkeiten,
mehrstufige
Zufallsversuche und Baumdiagramme, Pfad-und
Summenregel,
Kombinatorik,
Taschenrechnereinsatz,
Simulation
mit
Zufallsziffern, Zufallsgeräte.
Heinz Klaus Strick: Stochastik mit Excel. In:
Beiträge zum Mathematikunterricht 2003. Vorträge
GDM 2003 . Hildesheim: Franzbecker. 2003.S.
625-628
Im Vortrag werden Beispiele vorgestellt, in denen
sich der Einsatz von EXCEL bewährt hat:
Erzeugung von Pseudozufallszahlen, Überprüfung
von Kriterien für die ''Zufälligkeit'', Simulation von
34
Zufallsversuchen,
Berechnung
von
Wahrscheinlichkeitsverteilungen
und
deren
Kenngrößen, Entdeckung von Gesetzmäßigkeiten,
Vereinfachung
von
Rechenalgorithmen,
Auswertung von größeren Datenmengen im
Rahmen
des
Unterrichts
oder
in
Unterrichtsprojekten.
Reinhard Viertl: Einführung in die Stochastik (mit
Elementen der Bayes-Statistik und der Analyse
unscharfer Information). Wien: Springer, 2003 (3.,
überarbeitete und erweiterte Auflage)
Das bewährte Lehrbuch bietet eine Einführung in
die Wahrscheinlichkeitsrechnung und schließende
Statistik.
Es
werden
die
verschiedenen
Wahrscheinlichkeitsbegriffe (z.B.: klassische,
geometrische, subjektive, unscharfe) dargestellt,
gefolgt von einer detaillierten Ausführung von
stochastischen Größen und Grundkonzepten sowie
den zugehörigen mathematischen Sätzen. Der
zweite Teil ist der klassischen schätzenden Statistik
gewidmet
und
bringt
Schätzfunktionen,
Bereichsschätzungen, statistische Tests und
Regressionsrechnung. Daran schließt sich die im
deutschen Sprachraum stiefmütterlich behandelte
Bayes-Statistik an. Das letzte Kapitel ist der
formalen Beschreibung unscharfer Daten (fuzzy
data) und deren statistischer Analyse gewidmet.
Dieser Teil ist völlig neu und wurde vom Autor
entwickelt. Zum besseren Verständnis wurde in der
zweiten Auflage eine Reihe zusätzlicher Übungen
eingebaut.
Helmut Wirths, Oldenburg: Sind deutsche Autos
anders als ausländische? . In: Materialien für
einen realitätsbezogenen Mathematikunterricht,
Band 8, herausgegeben von Hans-Wolfgang Henn
und Katja Maaß. Hildesheim, Berlin: Franzbecker,
2004, S. 107-117
In diesem Beitrag werden Überlegungen zur
Vorbereitung einer Unterrichtsreihe vorgestellt, in
der Methoden und Begriffe der explorativen
Datenanalyse (EDA) benutzt werden, ebenso
Arbeitsergebnisse aus dem Unterricht sowie
Beobachtungen beim Umgang mit den Begriffen
und Methoden der EDA. Großer Wert wird von
Anfang an darauf gelegt, die Schülerinnen und
Schüler beim Sammeln der Daten, bei der
Darstellung und Interpretation der Ergebnisse und
bei der Revision ursprünglicher Vorstellungen so
intensiv wie möglich mit einzubeziehen. Teile
dieser Unterrichtseinheit wurden in 8. Klassen, die
vollständige Einheit in Leistungs- und Grundkursen
der gymnasialen Oberstufe unterrichtet.
Gerhard König
35