Wachstumsfunktionen 2

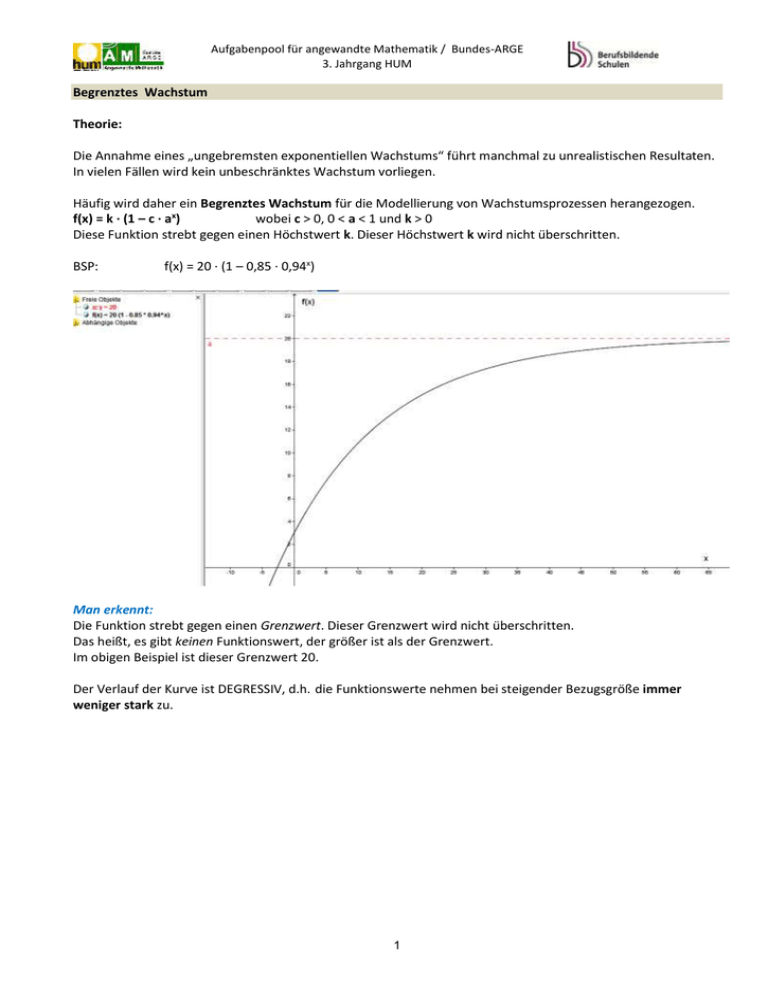
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
Begrenztes Wachstum
Theorie:
Die Annahme eines „ungebremsten exponentiellen Wachstums“ führt manchmal zu unrealistischen Resultaten.
In vielen Fällen wird kein unbeschränktes Wachstum vorliegen.
Häufig wird daher ein Begrenztes Wachstum für die Modellierung von Wachstumsprozessen herangezogen.
f(x) = k ∙ (1 – c ∙ ax)
wobei c > 0, 0 < a < 1 und k > 0
Diese Funktion strebt gegen einen Höchstwert k. Dieser Höchstwert k wird nicht überschritten.
BSP:
f(x) = 20 ∙ (1 – 0,85 ∙ 0,94x)
Man erkennt:
Die Funktion strebt gegen einen Grenzwert. Dieser Grenzwert wird nicht überschritten.
Das heißt, es gibt keinen Funktionswert, der größer ist als der Grenzwert.
Im obigen Beispiel ist dieser Grenzwert 20.
Der Verlauf der Kurve ist DEGRESSIV, d.h. die Funktionswerte nehmen bei steigender Bezugsgröße immer
weniger stark zu.
1
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3, B, C Funktion interpretieren
Zeichnen Sie die Funktion
N(t) = 20 ∙ (1 – 0,85 ∙ 0,94t)
N … Menge in Mengeneinheiten (ME)
t … Zeitdauer in Zeiteinheiten (ZE)
wobei D = R0+ (bei Textaufgaben meist nur für R0+ definiert).
Interpretieren Sie den Verlauf des Graphen der Funktion N (z.B. Monotonie, Anfangswert, Höchstwert …)
Lösung:
Die Funktion ist streng monoton steigend. Der Wachstumsverlauf ist degressiv.
Der Höchstwert ist
K = 20 ME
denn 20 ∙ (1 – 0,85 ∙ 0) = 20 ∙ (1 – 0) = 20 … Grenzwert
Der Anfangswert ist
N(0) = 3
denn 20 ∙ (1 – 0,85) = 20 ∙ 0,15 = 3
3 B,D Wachstumsmodell
Begründen Sie mit Hilfe von 2 Graphen, dass bei der Funktion
f(x) = 2 ∙ (1 – 0,5 ∙ ax)
0 < a < 1 gelten muss, damit ein Wachstum vorliegt! Verwenden Sie für a einen selbstgewählten Wert.
Lösung:
2
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B,C Bevölkerung
Im Jahr 1960 gab es ca. 3 ∙ 109 Menschen, bis 1977 wuchs die Zahl auf 4,1 ∙ 109 Menschen.
N … die Bevölkerungszahl in Milliarden (Mia1).
t … Jahre (a) nach 1960.
Wie viele Menschen würden im Jahr 2050 auf der Erde leben, wenn man degressives Wachstum zu Grunde legt
und annimmt, dass auf der Erde höchstens K = 20 ∙ 109 Menschen leben können?
a.) Geben Sie zunächst eine Formel der Form N(t) = K ∙ (1 – c ∙ at) an und zeichnen Sie den Graphen der
Funktion N! Berechnen Sie dazu aus den gegebenen Informationen die Werte für K, a und c!
b.) Berechnen Sie, wie viele Menschen nach dieser Modellannahme 2050 auf der Erde leben würden!
c.) Wann würden i) 10 Milliarden bzw. ii) 18 Milliarden Menschen auf der Erde leben?
d.) Was bedeuten die Ausdrücke N51 – N0 bzw. K – N51 in diesem Zusammenhang?
Lösung:
a.) Ansatz:
N(t)= K ∙ (1 – c ∙ at)
I: N(0) = 20 ∙ (1 – c ∙ a0)

17
II: N(17) = 20 ∙ (1 – c ∙ a )

0,85 ∙ a17 = 1 – 0,205

Wegen K = 20
3 = 20 ∙ (1 – c) 
4,1 = 20 ∙ (1 – c ∙ a17)
0,85 ∙ a17 = 0,795
folgt: N(t) = 20 ∙ (1 – c ∙ at)
c = 1 – 0,15 = 0,85

0,205 = 1 – 0,85 ∙ a17

a17 = 0,93529….
a = 17 0,93529... ≈ 0,996072777
Funktionsgleichung: N(t) = 20 ∙ (1 – 0,85 ∙ 0,996t)
b.) t = 2050 – 1960 = 90
N(90) = 20 ∙ (1 – 0,85 ∙ 0,99690) = 8,07 also 8,07 ∙ 109 Menschen
c.) i.) Ansatz:
10 = 20 ∙ (1 – 0,85 ∙ 0,996t)  t = 134,8 ≈ 135
1960 + 135 = 2095
D.h.: Im Jahr 2095 werden ca. 10 Milliarden Menschen leben.
ii.) Ansatz: 18 = 20 ∙ (1 – 0,85 ∙ 0,996t)
 t = 543,86 ≈ 544
1960 + 544 = 2504
D.h.: Im Jahr 2504 werden ca. 18 Milliarden Menschen leben.
1
Eine andere Abkürzung für Milliarde ist Mrd!
3
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
d.)
N(51) – N(0) = N(vom Jahr 2011) – N(vom Jahr 1960)
Gibt an, um wie viel Menschen nach dieser Annahme im Jahr 2011 mehr auf der Erde leben, als im Jahr
1960
K – N(51) = 20 Milliarden – N(vom Jahr 2011)
Gibt an, wie viele Menschen im Jahr 2011 nach dieser Modellannahme noch auf der
Erde Platz hätten, wenn man davon ausgeht, dass 20 Milliarden der Höchstwert ist.
3A,B,C Grippe
Eine Grippeinfektion in einer Population von 10 000 Personen verläuft näherungsweise nach der Formel für
begrenztes Wachstum.
N … Anzahl der infizierten Personen in Zehntausend (ZT)
t… Zeitdauer in Tagen (d)
Es sei N(0) = 15 und N(10) = 400.
a) Stellen Sie eine Formel für N(t) auf.
b) Berechne, wie viele Personen nach 30 Tagen infiziert sind.
c) Berechnen Sie, wie viele Personen nach 60 Tagen noch nicht infiziert sind.
d) Ermitteln Sie, wann 95 % der Population infiziert sind. Stellen Sie die Situation grafisch dar.
Lösung: Die Werte erhält man, wenn man Zwischenergebnisse abspeichert und nicht rundet!
a.) Ansatz:
N(t) = K ∙ (1 – c ∙ at)
Wegen K = 10 000 folgt:
N(t) = 10 000 ∙ (1 – c ∙ at)
I: 15 = 10000 ∙ (1 – c) 
c = 1 – 0,0015 = 0,9985
II: 400 = 10000 ∙ (1 – c ∙ a10)  0,04 = 1 – 0,9985 ∙ a10
0,9985 ∙ a10 = 1 – 0,04

0,9985 ∙ a10 = 0,96
 a10 = 0,961442….
a = 10 0,961442... ≈ 0,996075634 Speichern
Funktionsgleichung: N(t) = 10 000 ∙ (1 – 0,9985 ∙ 0,996…t)
b.) N(30) = 1126
c.) 10000 – N(60) = 10000 – 2113 = 7887
d.) 95% von 10000 = 9500
Ansatz: 9500 = 10 000 ∙ (1 – 0,9985 ∙ 0,996…t)
0,95 = 1 – 0,9985 ∙ 0,996…t
0,996…t = 0,050075…  t = 761,5
Also nach ca. 762 Tagen
4
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3A,B,C Tierpopulation
Eine Tierpopulation in einem bestimmten Gebiet bestand zu Beginn des Beobachtungszeitraums aus zehn
Tieren. Drei Jahre später waren es 77 Tiere. Man nimmt an, dass in diesem Gebiet nicht mehr als 1 000 Tiere
dieser Art leben können.
N … Anzahl der Tiere in ME, 1 ME = 100 Tiere
t … Zeitdauer in Jahren (a)
a) Stellen Sie, unter der Annahme, dass begrenztes Wachstum vorliegt, eine Formel für N auf .
b) Berechnen Sie, wie viele Tiere nach zehn Jahren (seit Beginn gerechnet) in diesem Gebiet leben werden!
c) Nach wie vielen Jahren werden ca. 800 Tiere in diesem Gebiet leben?
Zeichnen Sie den Graphen der Funktion N für diesen Fall.
Lösung:
a)
N(0) = 10
N(3) = 77
K = 1000
Lösungsansatz rechnerisch über ein Gleichungssystem
I: 10 = 1000 ∙ (1 – c) 
c = 1 – 0,01 = 0,99
II: 77 = 1000 ∙ (1 – c ∙ a3) 
0,077 = 1 – 0,99 ∙ a3
0,99 ∙ a3 = 1 – 0,077

0,99 ∙ a3 = 0,923
a = 3 0,9323232... ≈ 0,97691213
Funktionsgleichung: Nt = 1 000 ∙ (1 – 0,99 ∙ 0,9769t)
b) N(10) = 216,23
 ca. 216 Tiere
c) Nach ca. 68,5 Jahren
5


N(t) = 1 000 ∙ (1 – c ∙ at)
a3 = 0,93232323….
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3A,B,C,D Absatz
Der Absatz einer neuen Schuhcreme hängt vom Werbeaufwand ab. Man schätzt, dass zwischen dem
Werbeaufwand x und dem Absatz A folgender Zusammenhang besteht:
A(x) = d ∙ (1 – ax) + b, wobei 0 < a < 1, b > 0, d > 0
A … Absatz in Mengeneinheiten ME
x … Kosten für die Werbung in Geldeinheiten
a) Skizzieren Sie den Verlauf dieser Funktion für a = 0,9, b = 1 und d = 1
b) Ermitteln Sie, welchen Absatz man ohne Werbung erzielen würde.
c) Argumentieren Sie, welcher Absatz auch bei noch so großen Werbeaufwand nicht überschritten werden kann.
d) Drücken Sie x durch A, a, b und d aus!
e) Was bedeutet A(x) < A(2x) in diesem Zusammenhang?
Lösung:
a)
A(x) = 1 ∙ (1 – ax) + 1 = (1 – ax) + 1 = 1 – ax + 1 = 2 – ax
Höchstwert bei 2
b) b
c) d + b
d)
Der Schnittpunkt mit der zweiten Achse ist (0 / 1)
denn: A(0) = d ∙ (1 – a0) + b = d ∙ (1 – 1) + b = d ∙ 0 + b = 0 + b = b
denn: d ∙ (1 – 0) + b = d ∙ 1 + b = d + b
 A b
lg 1  x

d 
x 
lg a
oder
 d  Ax  b 
lg 

d


x
lg a
e) Wenn man den Werbeaufwand verdoppelt, macht man mehr Absatz, als ohne Verdoppelung.
6
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3 A,B,C,D Lösung
Beim Auflösen einer Substanz in einer Flüssigkeit ist die nach
t Sekunden aufgelöste Substanzmenge gegeben durch
M(t) = S ∙ (1 – e λt)
M … aufgelöste Menge in Gramm (g)
S … Sättigungsmenge in Gramm pro Liter (g/l)
t … Dauer in Sekunden (s)
a) Beim Auflösen von Benzoesäure in Wasser (S = 28 g/l) beträgt die gelöste Menge nach 30 Sekunden 15,5 g.
Berechnen Sie λ! Zeichnen Sie den Graphen von M!
b) Berechnen sie, nach welcher Zeit 90 % der Sättigungsmenge S aufgelöst sind.
c) Erklären Sie, was bedeutet M(2) < M(5) in diesem Zusammenhang bedeutet.
d) Erklären sie, was durch M(5) – M(2) angegeben wird.
Lösung:
a)
λ = – 0,026882529

M(t) = 28 ∙ (1 – e-0,026882529∙t)
Lösungsansatz: M(t) = 28 ∙ (1 – eλt)
M(30) = 28 ∙ (1 – e λ ∙ 30)
15,5 = 28 ∙ (1 – e30λ)
λ = – 0,806475866 / 30 = – 0,026882529
b)
nach ca. 85,7 Sekunden.
Lösungsansatz: 90 % von 28 = 25,5
25,2 = 28 ∙ (1 – e-0,026882529∙t)
t = 85,65 Sekunden
c)
dass nach 2 Sekunden weniger aufgelöst ist, als nach 5 Sekunden.
d)
Wie viel Substanz innerhalb dieser 3 Sekunden (also im Zeitintervall [2 ; 5]) aufgelöst
wurde.
7
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
3. Jahrgang HUM
3,A,B,C,D Medikament
Die Konzentration eines (in Tablettenform verabreichten) Medikaments im Blut ist gegeben durch
y(t) = s ∙ (1 – e λt)
y … Konzentration des Medikaments im Blut in Milligramm pro Liter Blut (mg/l)
s … Sättigungswert in mg/l
t… Zeitdauer in Stunden (h)
a) Berechnen Sie λ, wenn in einer halben Stunde die Konzentration y auf die Hälfte des
Sättigungswertes s steigt!
b) Begründen Sie, warum y(0) = 0 ist! Bestimmen Sie allgemein y(1) und skizzieren Sie den Graphen von y!
c) Ermitteln Sie, wann die Konzentration 90% des Sättigungswertes erreicht hat?
(Der Abbau des Medikaments während der fraglichen Zeit wird vernachlässigt.)
d) Erklären sie, was bedeutet y(1,2) > y(0,8) in diesem Zusammenhang bedeutet.
e) Erklären Sie, was durch y(1,2) – y(0,8) angegeben wird.
Lösung:
a)
λ = – 1,386294361

y(t) = s ∙ (1 – eλt)
y(0,5) = s ∙ (1 – eλ ∙ 0,5)
λ = (ln(0,5))/0,5 = – 1,386…
y(t) = s ∙ (1 – e-1,386294361∙t)
y(0) = s ∙ (1 – e-1,386294361∙0) = s ∙ (1 – e0) = s ∙ (1 – 1) = s ∙ 0 = 0
y(1) = s ∙ (1 – e-1,386294361∙1) = s ∙ (1 – e-1,386294361) = s ∙ (1 – 0,25) = s ∙ 0,75 = 0,75 ∙ s
b)
Zeichnen Mit GG:
c)
Für s einfach 100 eingeben, dann hat man es prozentuell dargestellt.
nach 1,66 Stunden
Lösungsansatz: 90 % von s = s ∙ 0,9
s ∙ 0,9 = s ∙ (1 – e-1,386294361∙t)
0,9 = 1 – e-1,386294361∙t
t = (ln 0,1) / – 1,386294361 = 1,66 Stunden
d)
e)
… dass die Konzentration des Medikaments im Blut 1,2 Stunden nach der Einnahme
höher war als 0,8 Stunden nach der Einnahme.
Gibt an, um wie viel die Konzentration nach 1,2 Stunden größer war,
als nach 0,8 Stunden.
8