Notwendige und hinreichende Kriterien für innere Extremwerte

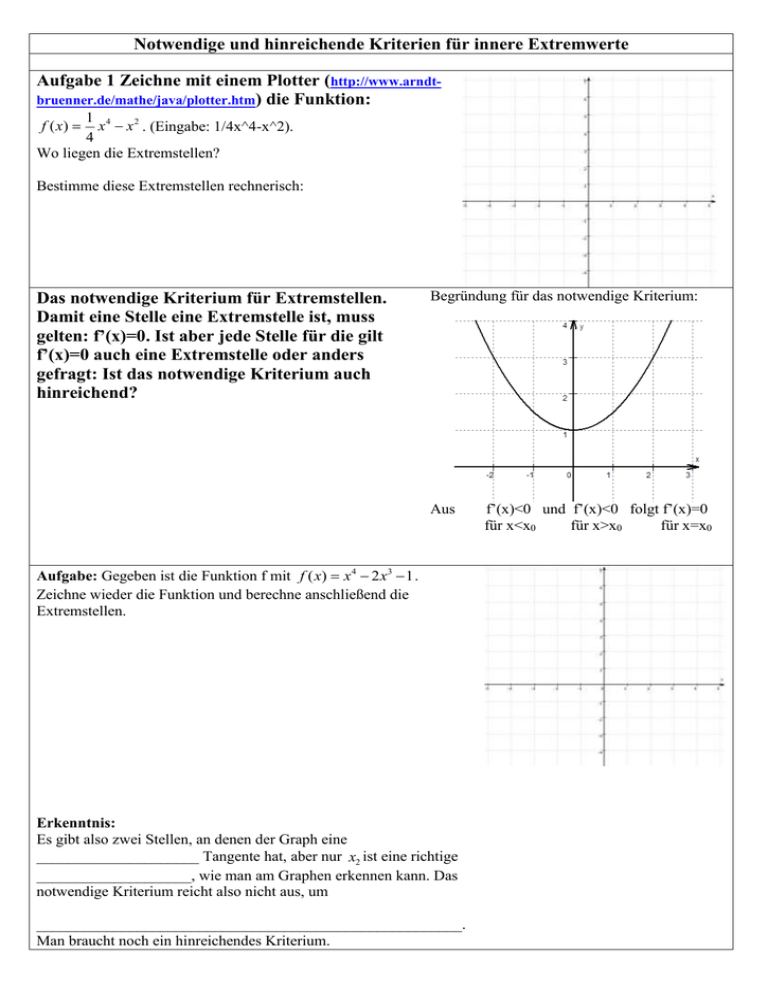
Notwendige und hinreichende Kriterien für innere Extremwerte
Aufgabe 1 Zeichne mit einem Plotter (http://www.arndtbruenner.de/mathe/java/plotter.htm) die Funktion:
1 4
x  x 2 . (Eingabe: 1/4x^4-x^2).
4
Wo liegen die Extremstellen?
f ( x) 
Bestimme diese Extremstellen rechnerisch:
Das notwendige Kriterium für Extremstellen.
Damit eine Stelle eine Extremstelle ist, muss
gelten: f’(x)=0. Ist aber jede Stelle für die gilt
f’(x)=0 auch eine Extremstelle oder anders
gefragt: Ist das notwendige Kriterium auch
hinreichend?
Begründung für das notwendige Kriterium:
Aus
Aufgabe: Gegeben ist die Funktion f mit f ( x)  x 4  2 x3  1 .
Zeichne wieder die Funktion und berechne anschließend die
Extremstellen.
Erkenntnis:
Es gibt also zwei Stellen, an denen der Graph eine
_____________________ Tangente hat, aber nur x2 ist eine richtige
____________________, wie man am Graphen erkennen kann. Das
notwendige Kriterium reicht also nicht aus, um
_______________________________________________________.
Man braucht noch ein hinreichendes Kriterium.
f’(x)<0 und f’(x)<0 folgt f’(x)=0
für x<x0
für x>x0
für x=x0
Hinreichende Bedingung für innere Extrema. Das Vorzeichenwechselkriterium
Betrachten wir die Extrempunkte genauer:
Hochpunkt (Maximum)
Tiefpunkt (Minimum)
Keine Extremstelle
Für x<x0 gilt f’(x) _______
Für x<x0 gilt f’(x) ________
Für x<x0 gilt f’(x) _______
Für x>x0 gilt f’(x) _______
Für x>x0 gilt f’(x) ________
Für x>x0 gilt f’(x) _______
Das Vorzeichenwechselkriterium (positive oder negative Steigung) gibt also nun eindeutig an:
1. (Bzgl. Existenz)__________________________________________________________________________
_________________________________________________________________________________________
2. (Bzgl. Art der Extrempunkte) ______________________________________________________________
_________________________________________________________________________________________
Damit ist das VZW nicht nur ein notwendiges, sondern auch ein ____________________________ Kriterium.
Anwendung des VZW:
Prüfe mit den VZW, ob die Stellen x1  0 und x2  1,5 der oberen Funktion wirklich Extremstellen sind.
Lösung:
Weg:
Alternative Formulierung des hinreichenden Kriteriums, über das Monotonieverhalten von
f’(x), also über die Steigung der Steigungsfunktion oder anders ausgedrückt das Verhalten von
f’’(x).
Hochpunkt (Maximum)
Tiefpunkt (Minimum)
Keine Extremstelle
Ableitungsfunktion:
Ableitungsfunktion:
Ableitungsfunktion:
Dies bedeutet für die Steigung der
1. Ableitung, also für f’’(x) an der
Stelle x0:
Dies bedeutet für die Steigung der
1.Ableitung, also für f’’(x) an der
Stelle x0:
Dies bedeutet für die Steigung der
1.Ableitung, also für f’’(x) an der
Stelle x0:
f’’(x0) __________
f’’(x0) __________
f’’(x0) __________
Daraus kann man ein anderes hinreichendes Kriterium formulieren:
f sei auf einem Intervall J zweimal differenzierbar und x0 eine innere Stelle von J.
f’(x0) ___ und f’’(x0) ___
Dann gilt: Ist
______________
, dann ist f(x0) ein
f’(x0) ___ und f’’(x0) ___
.
______________
Anmerkung: Gilt f’(x0) = 0 und f’’(x0) = 0, dann ________________________________________________
Aufgabe: Prüfe mit dem zweiten Kriterium, ob die Stellen x1  0 und x2  1,5 der oberen Aufgabe wirklich
Extremstellen sind.
f ' ( x)  __________________
f ' ' ( x)  _____________________
Lösung: f ( x)  x 4  2 x3  1
Prüfe: x1  0
_______________________
Also ____________________________________________.
Prüfe: x1  1,5
________________________
Also ___________________________________________ .
Schlussbemerkung:
Um von einer Funktion die Extremstellen zu finden, geht man also üblicherweise folgendermaßen vor:
1. Setze _________________________________________________________________________________.
2. Setze _________________________________________________________________________________.