Gaub-E1-2-2

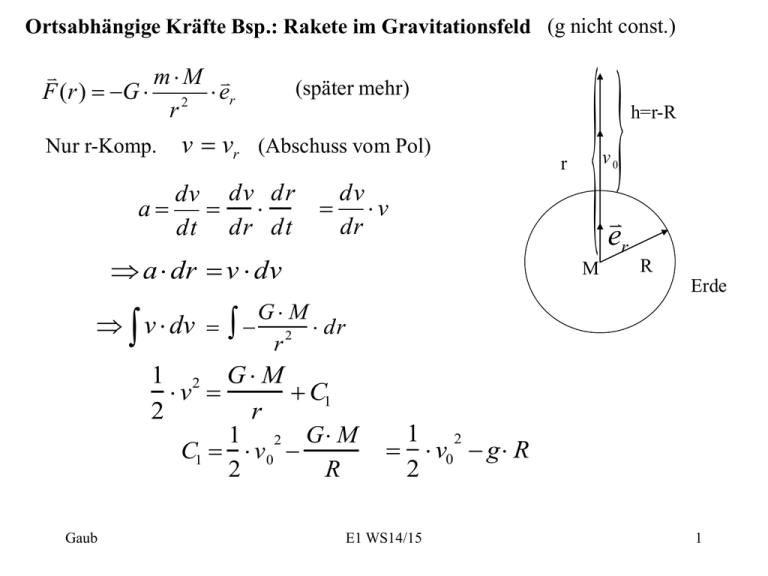
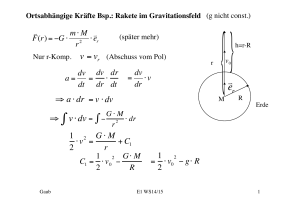
Ortsabhängige Kräfte Bsp.: Rakete im Gravitationsfeld (g nicht const.)

mM 
F (r )  G  2  er
r
Nur r-Komp.
(später mehr)
v  vr (Abschuss vom Pol)
dv dv dr
a


dt dr dt
dv
 v
dr
 a dr  v  dv

r
}{
h=r-R
v0

er
M
R
Erde
G M
 v  dv 
  r 2  dr

1 2 G M
v 
 C1
2
r
1 2 G M
C1   v 0 
2
R
Gaub
1 2
  v0  g R
2
E1 WS14/15
1



1 2 GM 1 2
v 
  v0  g  R
2
r
2
mit a(R)  g  G 
M
2
R
r
1 2 g  R2 1 2
 v 
  v0  g  R
2
r
2
R
 rmax 

2
v0
1 (
)
2Rg
km

11.2

v0  v2  2  R  g
s
}{
v0

er
v(rmax )  0
M
für
h=r-R
R
Erde
v0  2  R  g
Fluchtgeschwindigkeit
(2.kosmische Geschwindigkeit)
Kleinste Kreisbahn (Newton) 1. Kosmische Geschwindigkeit
2
v2
G M
v1 G  M
  v1 
 g R 

2
2
R
R
R
Gaub
E1 WS14/15
 7.9
km
s
2

Newtons Sicht:
Gesamtimpuls dp
dv
dv dm
dm


m


m



v

 v (m  m)  g
(Rakete+Gas)
dt
dt
dt dt
dt
Näherung
0
dm dm
Rakete
Ausstoßgeschwindigkeit
m v
ve  v  v  const 
relativ zur Rakete


m v 
bezogen auf
RaketenGas Eroberfläche 
dv
dm
m  
 ve  m  g
gleichung

dt
dt
Triebwerks-Schub
m
m0

mT
 dv  ve 
v (T )
0
T
t

Gaub

dm
 g  dt
m
m (T )
Nur z-Richtung
T
1
v (0)dv  ve  m(0) m  dm  0 g  dt 
v(T )  ve (ln mT  ln m0 )  g  T
m0
Viel Treibstoff
 v(T)  v e  ln
 g T schnell verbrennen
mT
E1 WS14/15
3
Bsp.: 1. Stufe Saturn V
km
s
m0  3106  kg
ve  4 
}
km
 v(T)  4,4 
s
g0
km
 v(T)  3,4 
s 2
g

9,81m
/s

mT 1106  kg
T 100 s
 unterhalb der Fluchtgeschwindigkeit

 Mehrstufige Trägerraketen
Apollo 11 Saturn V lauch
http://www.youtube.com/watch?v=wvWHnK2FiCk
Gaub
E1 WS14/15
4
§2.7 Energiesatz der Mechanik
 
dW  F  dr
Arbeit + Leistung
W12
Bahnkurve
 
  F  dr
p2
Linienintegral
p1
 
d
r
 v  dt
z
P2
„Arbeit“[W]= Nm = Joule
z
  x2   y 2 
 2 
 F  dr   Fx  d x   Fy  d y   Fz  d z
p2

F
p1

r (t )
x1


Anmerkung: W = 0 fürF  dr
P1
y
Leistung:
x
Bsp. Gleichförmige Kreisbewegung:

Bsp.: Dehnarbeit einer Feder von 0  x :
dW
P
 Fv
dt
y1
z1
[P]=
J
=Watt=W
s


v  v  et ; F  F  er
 
 F  dr  0  W  0
W  Fx  d x
x
  D  x  dx
0
1
2
  D x
2
Gaub
E1 WS14/15
5
Konservative Kraftfelder
 
WI   F  dr
P2
I
z
P1
v
Ft
P1

 
WII   F  dr
P2
II
P2
P1
v
dr
r ( t)
Wenn WI  WII  WIII  
=> Integral wegunabhängig
y


v
 Kraftfeld F(r) konservativ
x
Konservatives Kraftfeld:
 
WI  WII   F  dr 
 
F
  dr
P2
P1
P1
I
P2
II
  P1  
 
  F  dr   F  dr   F  dr  0
P2
P1
II
P2
I
Die Arbeit hängt nur von Start- und Endpunkt, nicht vom Weg ab.
Vektoranalysis: Stokes´scher Satz  konservativ falls rot F  0
Gaub
E1 WS14/15
6

0
  
Fr   0 
F 
 z
Bsp.: homogenes Kraftfeld
z
P2
z2
WI   F  dr
P2
II
P1
z2
 0   Fz  dz
z1
22
z1
WII   Fz  dz  0
I
P1
x1
z1
x2
 
  F  dr  0 
x
Konservatives Kraftfeld

Bsp.: zentrales Kraftfeld F  f (r )
  r2
 F  dr   Fr  dr  0
P2
P2
P1
II

   Fr  dr
r1
 
F  dr  0 
r1
r2
konservativ
I
P1
Gaub
E1 WS14/15
7
Potentielle Energie
konservatives Kraftfeld 
P2
  Def !
W   F  dr  E p (P1 )  E p (P2 )  E p
P1
v
F

dr

Bemerkung:
I. Vorzeichen so gewählt, dass Arbeit, die am Körper am
Körper verrichtet wird, dessen E p erhöht

WP 
 
  F  dr
 E p (P) 
Arbeit die geleistet wird um P
ins Unendliche zu bringen
P
II. Nullpunkt wird oft so gewählt, dass E p ()  0
Gaub
E1 WS14/15
8
Bsp. Gravitationsfeld
Nahe Erdoberfläche  g = const.
 
W   F  dr
mit
h
   m  g  dz  m  g  h  E p (0)  E p (h)
0
E p (0)  0  E p (h)  m  g  h
Geleistete Arbeit hat zur Zunahme der E p geführt

Für grösseren Entfernungsbereich gilt das Gravitationsgesetz
GM m
GM m
GM m  
 E p (r)  E p ()
 dr  
 W  
 er  dr   
2
2
r
r
r
r
r


Ep
R
m  g  R
Gaub
r
GM m
Ep  
r
E1 WS14/15

9
Energiesatz der Mechanik 

dv
F  m

dt

t
 
dv 
t F  v  dt   m  t dt   v  dt 
t
0
konservatives Kraftfeld
0
P
 
 
 F  v  dt    F  dr  E p (P0 )  E p (P)  W
t
t0
P0

v1
t
dv 
 
m
 v  dt   m   v  dv
dt 
t0
v0
Def.:
Ekin

m 2 m 2
 v1   v0
2
2
m 2
 v
2
 Ekin  W
Die Zunahme der kinetischen Energie eines
Körpers ist gleich der an ihm geleisteten Arbeit
E  E p (P0 )  Eki n(P0 )  E p (P) Ekin (P)
 Im konservativen Kraftfeld ist die Summe aus
potentieller Energie und kinetischer Energie konstant

Gaub

E1 WS14/15
10
Bsp: freier Fall
v(h)  0 ; z  h ; E P (0)  0
z
EP ( z )     m  g  dz  m g z
0
m 2 m
Ekin ( z )   v   ( g  t ) 2  m  g (h  z)
2
2
E  E P (z)  E ki n (z)  m g h
Gaub
E1 WS14/15
Unabhängig von z!
11

F ( x  x, y  y )
Potential  Kraftfeld
P

r
P
E P 
E P (x  x,y  y)

F ( x, y )
y
E P
E
E
 x  P  y  P  z
x
y
z
Dafür benötigte Arbeit
E P (x, y)
 
W  F  dr  EP
x
 E

E
E
 Fx  x  Fy  y  Fz  z   P  x  P  y  P  z 
y
z
 x

Def.: Potential = Potentielle Energie pro Masse
ME
r
=> Schwerkraft F(r)  grad(V)m
Bsp.: Gravitation
Gaub

V(r)  G
 EP 


Nabla
 x 
  EP 
  grad ( EP )  EP
F 
 y 
 E 
 P
 z 
E1 WS14/15

12
Bestimmung von G, Bsp: Gravitationswaage
= 2 L FG
Drehmoment des
verdrillten Fades

Schema Gravitationswaage
Gaub
E1 WS14/15
13
Drehimpuls
Ebene beliebig gekrümmte Bahn

L
 
r (t ), v (t )

 v
r (t 2 )
O 

r (t )
m
vr
In Polarkoordinaten:

  
 
 
L  m(r  (vr  v ))  m(r  vr )  m(r  v )


p  mv
vv
0 weil r vr


und
v
r
Ebene von
 
weil r  v  r 2   
Kreisbewegung:
Gaub
Def.: Drehimpuls
  
 
L  (r  p)  m  (r  v )

 
L  r ,  v
  
;
v  v 

E1 WS14/15

L  m  r 2  

L  m  r 2  
14
Drehmoment:
Newton



dL  dr     dp 
 
 
   p   r    (v  p)  (r  p )  (r  F )
dt  dt
dt 
 
v v
0 weil v p
Def: Drehmoment
D


dL 
 

 D  (r  F )
dt
.

r

Für zentrale Kraftfelder

F  f (r )  eˆr

 L = const. bzgl. Kraftzentrum
ist
.
v
F
 
D0

 Drehimpulserhaltung
Zeitliche Veränderung des Drehimpulses ist gleich dem wirkenden Drehmoment
Gaub
E1 WS14/15
15


Man Beachte: L und D werden bzgl. eines festen Punktes O im Raum definiert
O1

L1  0

v
m
Gerade Bewegung kann Drehimpuls
haben bzgl. O2

r

L2  m  r  v  sin  0
O2
Analogie:
Später noch:
Gaub

r
v
F
p



D

L
m
I
E ki n
E ro t
E1 WS14/15
16
Johannes Keppler
Tycho Brahe
Gaub
E1 WS14/15
17
Planetenbewegung:
Kepplergesetze
(Basierend auf Beobachtung Tycho Brahes))
I. Planeten bewegen sich auf Ellipsen mit Sonne im Brennpunkt
II. Fahrstrahl von Sonne zu Planet überschreitet in gleichen Zeiten gleiche Flächen
P(t1 )
A1
A2
S
P(t2  t)
P(t2 )
P(t1  t)
III. Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die 3. Potenzen
ihrer großen Halbachsen
T12 a13
2 
3
T2
a2
Gaub

oder
Ti 2
3  const
ai
E1 WS14/15
für alle Planeten
18
Zum 2. Kepplerschen Gesetz

r (t  dt )
S

dA
v
r (t )
 
ds  v  dt
h
ds

p
Bogen ≈ Sehne
1
 dA   r  v  dt  sin 
2

dA 1
1  
1

  r  v  sin  
rp 
L
dt 2
2m
2m
+ 1. Gesetz (planare Bahn) => Richtung L konst

 L  const
Gaub
E1 WS14/15
19
Newtons Analyse:
!!
Planetenbahnen
Fallender Apfel

aus L  const. 
aus Actio = Reactio 
Selbe Axiomatik
Gravitation !
!!

FG (r )  f (r )  eˆr
(Zentralkraft)
FG ~ m1  m2

FG (r )  G  m1  m2  f (r )  eˆr
Mit Ellipse ~ Kreis => mp wp  rp  G  mp  ms  f (ri )
2
3. Keppler
mp  M S
w2 ~ T 2 ~ r 3 
 eˆr
 F  G 
2
2
r
 f (r) ~ r 
Newtonsches Gravitationsgesetz
Gaub

E1 WS14/15
20
Bestimmung von g: Mathematisches Pendel
Ft  m at
m  g  sin   m  l  

sin    
l
l (1 cos  )
3
3!

5
5!
...
sin   
Ft
Fr
   
g

l
m g
Lösung der DGL:
Gaub
  (t )  A  sin
g
t
l
 T  2  
l
g
g
E1 WS14/15
21
Genauer:
E p  m g  l  (1cos )
Ekin
m 2 m 2 2
  v   l  
2
2
Start
m 2 2
E  Eki n  E p  m  g  l  (1  cos  )   l    E p0  m  g  l  (1  cos 0 )
2
2  g  (cos   cos  0 )
d


l 0
 
g  0
T
4
dt

d
  dt  T
cos   cos  0 0
4

sin
mit sin  
sin
l
d
T  4

g 0 1  k 2  sin 2 
2
;
k  sin
l
1
2
T ( 0 )  2   
 (1    0  .....)
g
16
0
2


2
0
l
+ Bronstein oder
Mathematica
2
T ( 0 )
T0
1.02
 1.01
1.00
10
Gaub
E1 WS14/15
20 30
0
22
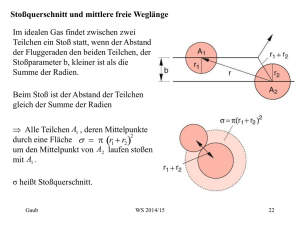
Kreisscheibe der Dicke dx schneidet aus der Kugelschale
der Dicke da das Volumenelement (Kreisring)
Gravitation Kugelschale
da
y
a
dV = 2  y ds dx,
y = asin,ds=da/sin
r
m
{
X
P
R
dm    2    a da dx
ds
m dm
 dEP  G 
r a
dx
EP  2      G  m  a  da  
r
x a
dx
r 2  y2  (R  x)2
R a
 2      a  da  m
EP 
 G   dr
R
r Ra
m m
EP  G 
R
 y  x  R 2 R x
2
2
2
a2

 a 2  R2  2  R  x
dx/dr r / R

dx/r dr/ R
Gaub
dV = 2  a dx da
mit

m  4    a2    da
E1 WS14/15
= Masse der KS
23
 Außerhalb der Hohlkugel erscheint die gesamte Masse konzentriert in O
EP
R
a
0
Innerhalb Hohlkugel:
G 
m  m
a
G 
m  m
R
R innerhalb der Kugel!
r a  R


F
a
0
EPi ~
R
F 0
F  G 
m  m
R2
 dr  2  R
r a  R
m  m
 EPi  G 
 const. R  a !
a
F  gradEP  0 für R < a

Gaub
E1 WS14/15
24
Varianten der Coulomb WW
Gaub
E1 WS14/15
25
Varianten der Coulomb WW
Siehe J.N. Israelachvili, Intermolecular and Surface Forces with Applications to Colloidal and
Biological Systems, Academic Press 1985
Gaub
E1 WS14/15
26
Bsp.: VdW-Potentiale ausgedehnter Körper
B


A
dw  nB 
2ydyd
(d   )
2
 y2

A
y

d
A
A
3
B
d
B
M
B
r
dy

wAB

nB 
   dw  
3
6
d
y 0  0
d
3
WAB~ 1/d
a)
b)
Nochmalige Integration
=> Potetial zwischen 2 Wänden
WAB  
H AB 1

2
d
12 d 2
HAB typisch ≈10-20 J
Hamaker Konstante
Gaub
a
 2 n A nB  1
12
WAB~ 1/d
L
c)
d
WAB~ 1/d
E1 WS14/15
R
5
d)
d
WAB~ 1/d
27
2