Kinematik Einführung Größen und ihre Einheiten

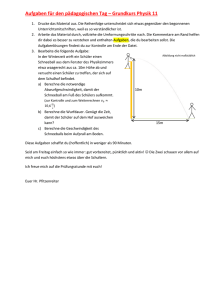
www.SchulLV.de
Basiswissen > Grundlagen > Kinematik
Kinematik
Skript PLUS
Lernvideos PLUS
Einführung
Die Kinematik ist ein Teilgebiet der Mechanik und ist die Lehre der
Bewegung von Punkten und Körpern im Raum.
Die Bezeichnung kommt von dem altgriechischen Wort κινημα [kinema]
für Bewegung.
Welche Kräfte wie auf die Masse oder den Körper wirken, spielt in der
Kinematik keine Rolle. Ursachen der Bewegung, also zum Beispiel
beschleunigende Kräfte, werden erst in der Dynamik, einer weiteren
Teildisziplin der Mechanik, betrachtet.
Größen und ihre Einheiten
Um die geradlinige Bewegung eines Körpers zu beschreiben, sind drei Größen erforderlich:
Anfangsposition
Anfangsgeschwindigkeit
Beschleunigung
Anfangsposition
Die Position, an der sich ein Körper oder eine Punktmasse zu Beginn der Betrachtung befindet, wird
durch den sogenannten Positionsvektor beschrieben. Ein solcher Vektor zeigt von einem festen
Bezugspunkt auf die Position des Körpers.
Ist der Bezugspunkt der Ursprung des Koordinatensystems, spricht man vom sogenannten
Ortsvektor.
Ein Ortsvektor gibt an, um wie viele Längeneinheiten man vom Ursprungspunkt in x -, um wie viele in
y - und um wie viele Einheiten man in z -Richtung laufen muss, um zur gesuchten Position zu
gelangen.
⎯→
In der rechts abgebildeten zweidimensionalen Skizze zeigt der Vektor B vom Ursprung zum Punkt B .
Diesen Punkt erlangt man, indem man 6,5 LE in x - und 3 LE in y -Richtung läuft.
1 von 7
www.SchulLV.de
B =
(
)
=
(
)
Der Vektor
⎯→
B
wird geschrieben als B
x
=
6, 5
(y)
=
(
3
)
Anfangsgeschwindigkeit
Die Geschwindigkeit wird in der Physik meist mit der Variablen
Anfangsgeschwindigkeit wird häufig als v0 bezeichnet.
Die Variable v kommt vom lateinischen Wort für Geschwindigkeit Velocitas.
v
bezeichnet.
Die
Die Geschwindigkeit = Durchschnittsgeschwindigkeit ist definiert als:
Δs
v =
Δt
Δs
ist dabei die zurückgelegte Strecke, Δt die dafür benötigte Zeit.
Ist die Geschwindigkeit konstant, gilt v
s
=
t
Möchte man nicht nur die Durchschnittsgeschwindigkeit, sondern die Momentangeschwindigkeit
berechnen, betrachtet man nur eine ganz kurze Strecke und eine ganz kurze Zeit! Sind diese
Abschnitte infinitesimal klein, schreibt man die Geschwindigkeit als:
ds
v =
dt
Die Geschwindigkeit ist die erste Ableitung der Strecke nach der Zeit: v
= ṡ=
ds
dt
Nach dem Internationalen Einheitensystem wird die Geschwindigkeit mit folgender Einheit
angegeben.
[s]
[v] =
[t]
Im Alltag wird meistens die Einheit
m
s
km
h
m
=
m
=
sec
s
verwendet. Beachte, dass du diese Einheit beim Rechnen in
umwandelst.
www.SchulLV.de
2 von 7
Merke:
m
s
⇒
⋅
km
km
3, 6
h
h
m
⇒
: 3, 6
s
In der Luft- und Seefahrt verwendet man eine andere Einheit: Knoten. Diese Einheit gibt nicht die
zurückgelegten Meter oder Kilometer pro Zeit, sondern die zurückgelegten Seemeilen pro Stunde.
Es gilt: 1 K noten
1 Seemeile
= 1kn =
sm
=
1 Stund e
km
= 1, 852
h
h
Beschleunigung
Die Beschleunigung
Geschwindigkeit an.
a
gibt in der Physik die Änderung der
Beschleunigung kennst du aus dem Alltag: fährst du mit dem
Fahrrad in die Schule und willst den langsamen Radfahrer vor dir
überholen, musst du schneller fahren als bisher, du musst
kräftiger in die Pedale treten und dadurch dein Fahrrad
beschleunigen.
Kommst du allerdings an eine rote Ampel, musst du anhalten,
also dein Fahrrad bis auf die Geschwindigkeit
m
v = o
s
abbremsen. Auch hier handelt es sich um eine Beschleunigung,
da sich deine Geschwindigkeit ändert. Hier spricht man allerdings
von einer sogenannten negativen Beschleunigung.
Die durchschnittliche Beschleunigung ist definiert als:
Δv
a =
Δt
Um die momentane Beschleunigung zu berechnen,
Momentangeschwindigkeit infinitesimal kleine Größen.
Es gilt:
verwendest
du
wie
bei
der
dv
a =
dt
Die Einheit der Beschleunigung kannst du dir aus der Definition dieser Größe herleiten.
m
[v]
[a] =
=
[t]
s
m
=
s
2
s
Die Beschleunigung ist die erste Ableitung der Geschwindigkeit
zurückgelegten Strecke s nach der Zeit t :
dv
a =
www.SchulLV.de
und die zweite Ableitung der
d s
= v̇ =
dt
v
2
dt
2
= s̈
3 von 7
Erdbeschleunigung
Regen, reife Äpfel und leider ab und zu auch das
Marmeladenbrot... Warum fallen diese Gegenstände zu
Boden?
Ursache hierfür ist die Erdbeschleunigung! Im PhysikLVSkript „Dynamik“ lernst du, dass sich zwei Massen nach
dem Gravitationsgesetz anziehen. Je größer diese Massen
sind, desto stärker ist die gegenseitige Anziehungskraft.
Die Erde mit ihren 5, 9736 1024 kg übt auf jeden Körper
in ihrem Umfeld, also auf das aus der Hand fallende
Marmeladenbrot, auf einen Apfel und sogar auf den Mond,
die sogenannte Gravitationskraft aus. Diese Kraft bewirkt eine Beschleunigung in Richtung des
Erdmittelpunktes.
⋅
Jeder Körper, der also nicht befestigt oder festgehalten wird, wird von der Erde angezogen und mit
der sogenannten Erdbeschleunigung g zu ihrem Mittelpunkt beschleunigt.
Für g gilt:
m
g = 9, 81
2
s
Beispielaufgabe:
Im Jahre 1666 saß einer Legende nach der junge Physiker
Isaac Newton unter einem Apfelbaum und dachte über
verschiedene physikalische Gesetze nach. Plötzlich
schreckte ihn ein herunterfallender Apfel auf, der ihm auf
den Kopf fiel. Der Apfel hing bisher 12 m über dem Kopf
von Isaac.
Wie lange ist der Apfel gefallen, bis er den Kopf des
Physikers traf?
Lösung:
Vernachlässige zunächst den Luftwiderstand. Nutze dann die Formel für den freien Fall:
1
s =
⋅ ⋅
a
2
t
2
⇒
⋅
⎯⎯⎯⎯⎯⎯⎯⎯
2
s
t =
√
a
In dieser Aufgabe wird der Apfel durch die Erdanziehung beschleunigt. Es gilt also a
Damit ergibt sich durch Einsetzen der gegebenen Werte:
⋅
⋅
√
a
⋅ ≈
.
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
2
12m
⎯⎯⎯⎯⎯⎯⎯⎯
2
s
t =
= g
=
√
9, 81
m
1, 56
2
s
Der Apfel fiel ca. 1,56 Sekunden lange, bis er auf Isaacs Kopf aufschlug.
Parabelwurf
www.SchulLV.de
4 von 7
Bestimmt hast du im Sport bemerkt, dass der Ball weiter fliegt,
wenn du ihn stärker wirfst, er also schneller durch die Sporthalle
fliegt!
Die Flugbahn des Balls folgt im Idealfall, also bei
Vernachlässigung des Luftwiderstands, dem Graphen einer
Parabel. Aus diesem Grund wird der waagrechte Wurf (du wirfst
den Ball in waagrechte Richtung) auch Parabelwurf genannt.
Die Parabelbahn kannst du mathematisch belegen, wenn du die
Bewegung in
betrachtest.
x
- und in
y
-Richtung getrennt voneinander
Die Geschwindigkeit des Balls in x -Richtung ändert
sich nur vor dem Abwurf, während du ihn von dir
wegstößt. Sobald der Ball aber deine Hände
verlässt, ändert sich seine Geschwindigkeit in x Richtung nicht mehr, da keine beschleunigende
Kraft mehr in x -Richtung auf ihn wirkt.
In x -Richtung legt er in der Zeit t die Strecke
x(t) = v x
t zurück.
⋅
In y -Richtung
wirkt
zu
jeder
Zeit
die
Erdbeschleunigung Richtung Boden, diese bleibt
während der ganzen Betrachtung konstant. Die
Geschwindigkeitskomponente
in
y -Richtung
dagegen wird durch die ständige Beschleunigung
immer größer.
−⋅ ⋅
Da die Beschleunigung, aber nicht die Geschwindigkeit, konstant ist, gilt für den zurückgelegten Weg
1
2
y(t) =
g
t .
2
Das Minuszeichen zeigt an, dass der Ball nach unten beschleunigt wird, seine Höhe also immer
geringer wird.
Aus diesen beiden Gleichungen kannst du die Variable t eliminieren. So erhältst du den
Funktionsterm für die gesamte Bewegung, da du beide Bewegungen immer zum gleichen Zeitpunkt
betrachtest.
1.Schritt: Beide Gleichungen nach t 2 umformen
www.SchulLV.de
5 von 7
1.
x(t)
⋅ ∣
∣
= vx
t
: vx
x(t)
t
=
beide Seiten quadrieren
vx
2
t
x (t)
2
=
2
vx
− ⋅ ⋅ ∣⋅− ∣
−⋅
1
2.
y(t)
=
g
t
2
(
2)
: g
2
t
2
2
=
y(t)
g
2. Schritt: Gleichungen gleichsetzen
x
2
−⋅
− ⋅ ⋅
2
=
2
vx
∣⋅ ∣ −
y
g
g
1
y
=
x
g
: (
2)
2
2
2
vx
Beispielaufgabe:
Florian will vom 7,5-Meter-Turm im Freibad
springen. Weil er die Mädchen aus seiner
Klasse unten am Beckenrand beeindrucken
möchte, nimmt er vorher sogar noch Anlauf
und springt mit vx
= 7, 2
km
h
vom Brett ab.
In welcher Entfernung zum Beckenrand trifft
er auf? Weitere Werte kannst du der Skizze
entnehmen.
Da Florians Geschwindigkeit in x -Richtung nach dem Absprung konstant bleibt, er in y -Richtung
aber durch die Erdanziehung beschleunigt wird, ist dieser Fall mit dem waagrechten Wurf
−⋅ ⋅
vergleichbar: Florian springt entlang einer Parabel, deren Graph mit dem allgemeinen Funktionsterm
y =
1
x
g
2
2
2
vx
beschrieben werden kann.
Die gegebene Geschwindigkeit musst du in
vx
= 7, 2
= 2
∣
km
h
m
umrechnen.
s
: 3, 6
m
s
Da er aus einer Höhe von 7,5 m springt, musst du die Parabel um diesen Wert nach oben
verschieben.
Nun erhältst du folgenden Term für Florians Flugbahn :
− ⋅ ⋅
− ⋅
1
y
=
2
=
x
9, 81
1, 23
www.SchulLV.de
x
2
2
2
2
+ 7, 5
+ 7, 5
6 von 7
Um zu ermitteln, wo Florian auf der Wasseroberfläche auftrifft, musst du die Nullstelle der Parabel
bestimmen, an der gilt y = 0 :
− ⋅
− ⋅
− ⋅
⋅
=
0
=
7, 5
=
7, 5
= 1, 23
6, 1
= x
−
y
x
1, 23
x
1, 23
x
1, 23
x
2
x
2
2
2
2
+ 7, 5
+ 7, 5
∣−
∣⋅−
∣
∣√
7, 5
(
1)
: 1, 23
⎯⎯
⎯
= 2, 47
Addiert man zum Ergebnis die 2 m, die der Sprungturm laut Skizze über den Beckenrand herausragt,
erhält man die gesuchte Antwort: Florian trifft 4,47
m
vom
Beckenrand
entfernt
auf
die
Wasseroberfläche auf.
Die Mädchen am Beckenrand sind begeistert!
www.SchulLV.de
7 von 7