Die Addition und die Subtraktion von Vektoren

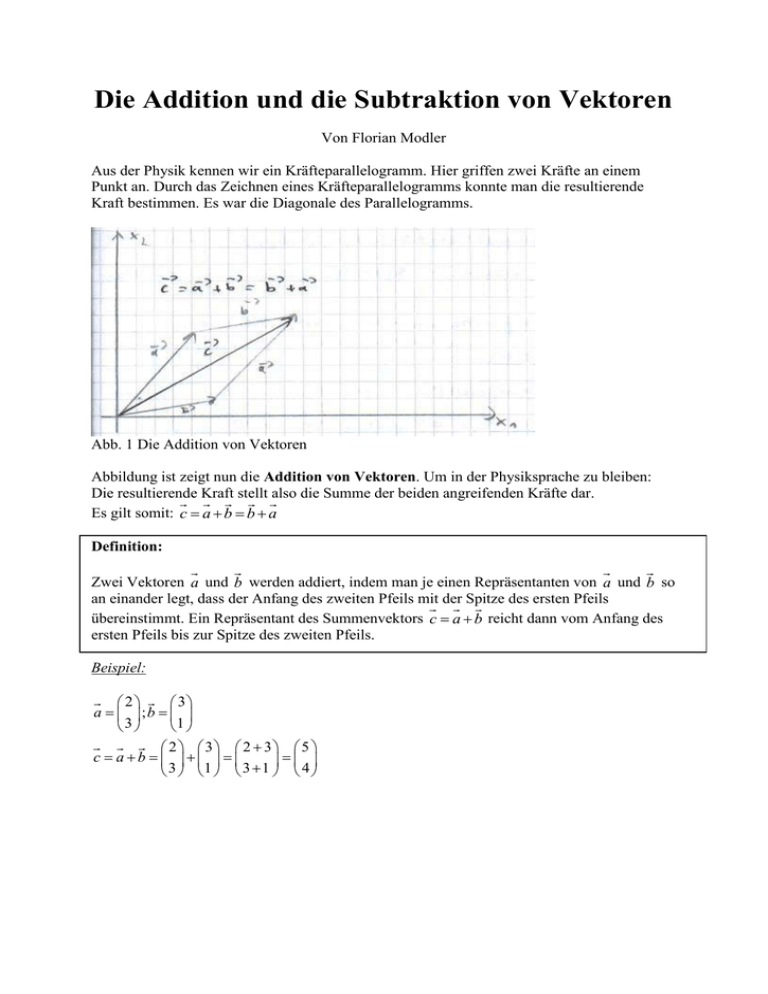
Die Addition und die Subtraktion von Vektoren
Von Florian Modler
Aus der Physik kennen wir ein Kräfteparallelogramm. Hier griffen zwei Kräfte an einem
Punkt an. Durch das Zeichnen eines Kräfteparallelogramms konnte man die resultierende
Kraft bestimmen. Es war die Diagonale des Parallelogramms.
Abb. 1 Die Addition von Vektoren
Abbildung ist zeigt nun die Addition von Vektoren. Um in der Physiksprache zu bleiben:
Die resultierende Kraft stellt also die Summe der beiden angreifenden Kräfte dar.
Es gilt somit: c  a  b  b  a
Definition:
Zwei Vektoren a und b werden addiert, indem man je einen Repräsentanten von a und b so
an einander legt, dass der Anfang des zweiten Pfeils mit der Spitze des ersten Pfeils
übereinstimmt. Ein Repräsentant des Summenvektors c  a  b reicht dann vom Anfang des
ersten Pfeils bis zur Spitze des zweiten Pfeils.
Beispiel:
 2
 3
a   ;b   
3
1 
 2   3  2  3  5 
c  ab      
 
 3  1   3  1   4 
Satz:
Zwei in Koordinatendarstellung gegebene Vektoren werden addiert, indem man ihre
entsprechenden Koordinaten addiert.
 a1   b1   a1  b1 
    

a  b   a2    b2    a2  b2 
 a  b   a  b 
 3  3  3 3
Wir können die Allgemeingültigkeit dieser Gleichungen aus der Pfeildarstellung der
Vektoraddition herleiten, wenn wir die drei Vektoren durch die Koordinatendifferenzen der
drei Punkte P(p1;p2;p3); Q(q1;q2;q3) und R(r1;r2;r3) darstellen:
 a1   q1  p1 
 b1   r1  q1 
 c1   r1  p1 
  

  

  

a   a2    q2  p2  ; b   b2    r2  q2  ; c   c2    r2  p2 
a  q  p 
b   r  q 
c  r  p 
3 
3 
 3  3
 3  3 3
 3  3
Wenn man die Koordinaten von a und b addiert, erhält man in der Tat die Koordinaten von
c , denn es gilt:
a1  b1  (q1  p1 )  (r1  q1 )  r1  p1  c1
a2  b2  (q2  p2 )  (r2  q2 )  r2  p2  c2
a3  b3  (q3  p3 )  (r3  q3 )  r3  p3  c3
Die Gesetze der Vektoraddition:
Abbildung 1 lässt zum Beispiel vermuten, dass auch in der Vektorrechnung das
Kommutativgesetz gilt. Wir wollen nun die uns aus der Menge der reellen Zahlen bekannten
Gesetze nachweisen und somit Gesetze der Vektoraddition kennen zu lernen.
1. Kommutativgesetz:
Satz: (Kommutativgesetz)
Für alle Vektoren a, b V gilt: a  b  b  a .
Beweis:
 a1   b1   a1  b1   b1  a1   b1   a1 
    
 
    
a  b   a2    b2    a2  b2    b2  a2    b2    a2   b  a
a  b   a  b  b  a  b   a 
 3  3  3 3  3 3  3  3
Der entscheidende Beweisschritt besteht in der Anwendung des Kommutativgesetzes für die
Addition reeller Zahlen in den einzelnen Koordinaten des Summenvektors.
Wir müssen uns immer wieder vor Augen führen, dass es keine Selbstverständlichkeit ist,
dass wir mit Vektoren genauso rechnen können, wie mit den reellen Zahlen. Aber wir können
die uns in den reellen Zahlen bekannten Gesetze zum Beweis anwenden.
2. Assoziativgesetz:
Satz: (Assoziativgesetz)
Für alle Vektoren a, b, c V gilt: (a  b)  c  a  (b  c) .
Beweis:
 a1   b1   c1   a1  b1   c1   b1  a1  c1 
      
   

(a  b)  c  [ a2    b2 ]   c2    a2  b2    c2    b2  a2  c2 
a  b  c  a  b  c  b  a  c 
 3  3  3  3 3  3  3 3 3 
 a1   b1  c1 
  

  a2   [ b2  c2 ]  a  (b  c)
a  b  c 
 3  3 3
Auch hier ist der entscheidende Beweisschritt in der Anwendung des Kommutativgesetzes für
reelle Zahlen.
Um das Neutralitätsgesetz anwenden und beweisen zu können, müssen wir das neutrale
Element und den Nullvektor definieren.
Aus der arithmetischen Definition der Vektoraddition ergibt sich unmittelbar, dass ein
neutrales Element für die Vektoraddition an allen Stellen die Koordinate 0 haben muss. Es gilt
nämlich:
 a1   0   a1  0   a1 
    
  
 a2    0    a2  0    a2 
 a  0  a  0   a 
 3    3
  3
Definition:
Unter dem Nullvektor 0 versteht man den Vektor, dessen sämtlichen Koordinaten Null sind.
0
 
0  0
0
 
Dem Nullvektor ordnet man jede Richtung und jede Orientierung zu.
Für den Betrag (die Maßzahl der Länge) des Nullvektors gilt: | 0 | 0
3. Neutralitätsgesetz:
Satz: (Neutralitätsgesetz)
Für jeden Vektor a V gilt: a  0  0  a  a .
Beweis:
 a1   0   a1  0   a1 
    
  
a  0   a2    0    a2  0    a2   a
 a  0  a  0   a 
 3    3
  3
 a1   0   0  a1   0   a1   a1 
    
      
a  0   a2    0    0  a2    0    a2    a2   a
 a  0 0  a  0  a   a 
   3  3
3
 3   
Um das Inversitätsgesetz zu definieren und zu beweisen, machen wir wieder einen kleinen
Einschub und zwar definieren wir vorher das inverse Element bzw. den Gegenvektor.
Wenn wir zu irgendeiner reellen Zahl a ihre Gegenzahl –a addieren, ergibt sich die Zahl 0,
also das neutrale Element der Addition.
Die Zahl – a ist daher – hinsichtlich der Addition – das inverse Element zur Zahl a.
Wir wollen untersuchen, ob es auch zu jedem Vektor a hinsichtlich der Vektoraddition einen
inversen Vektor b gibt.
Definition:
 a1 
 a1 


 
Der Vektor a   a2  heißt der Gegenvektor zum Vektor a   a2  .
 a 
a 
 3
 3
4. Inversitätsgesetz:
Satz: (Inversitätsgesetz)
Für alle Vektoren a V gilt a  (a)  (a)  a  0 .
Beweis:
 a1   a1   a1  (a1 )   a1  a1   0 
  
 
 
  
a  (a)   a2    a2    a2  (a2 )    a2  a2    0   0
 a   a   a  (a )   a  a   0 
3 
 3  3  3
 3 3  
Was bedeutet das graphisch?
Abb. 2 Graphische Darstellung des inversen Vektors
| a | 2²  3²  13
|  a | 2²  (3)²  13
Man erkennt, dass die Pfeile zu a und a sich jeweils nur durch ihre Orientierung
unterscheiden, dass sie aber gleich lang und zu einander parallel sind.
Satz:
Für jeden Vektor a und seinen Gegenvektor a gilt:
1) | a || a | 2)  a || a3)  a  a
Satz:
Für alle Vektoren a V gilt: ( a )  a .
Dreiecksungleichung:
Haben zwei Vektoren a und b verschiedene Richtungen, so bilden Vertreter von a , b und
a  b ein echtes Dreieck (siehe Abbildung 3). Da in jedem Dreieck die Summe zweier
Seitenlängen größer als die Länge der dritten Seite ist, gilt:
| a  b || a |  | b |
Man spricht bei dieser Beziehung von der Dreiecksungleichung.
Abb. 3 Dreiecksungleichung
Dagegen gilt für parallele und gleich orientierte Vektoren:
| a  b || a |  | b |
Abb. 4 Parallel und gleich orientierte Vektoren
Sind a und b entgegengesetzt orientiert, so sind zwei Fälle zu unterscheiden:
a) ist | a || b | , so gilt | a  b || a | , also erst recht | a  b || a |  | b | .
Abb. 5 Fall a)
b) ist | a || b | , so gilt | a  b || b | , also ebenfalls | a  b || a |  | b | .
Abb. 6 Fall b)
Nur wenn a  b ist, gilt also: | a  b || a |  | b |
Satz:
Zwei Vektoren a , b sind parallel und gleich orientiert genau dann, wenn gilt:
| a  b || a |  | b |
a  b | a  b || a |  | b | .
Subtraktion von Vektoren:
Abb. 7 Subtraktion von Vektoren I
Es gilt (siehe Abbildung 7): c  a  b  a  (b)
Man kann einen Vertreter des Differenzvektors a  b zeichnerisch auch dadurch bestimmen,
dass man zwei Vertreter der Vektoren a und b mit ihren Anfangspunkten aneinander legt;
dann reicht der Vertreter des Vektors a  b von der Spitze des zweiten Pfeils bis zur Spitze
des ersten Pfeils. (siehe Abbildung 7)
Ein weiteres Beispiel mit Koordinaten:
Abb. 8 Subtraktion von Vektoren II
Es gilt:
z  x  y  x  ( y )
3
 3 
x   ; y   
5
 3 
 3   3   3  (3)   6 
z  x y      
 
 5   3   5  (3)   8 
Definition:
Für beliebige Vektoren a, b V gilt:
a  b  a  (b) .
Satz:
Zwei in Koordinatendarstellung gegebene Vektoren werden subtrahiert, indem man ihre
entsprechenden Koordinaten subtrahiert:
 a1   b1   a1   b1   a1  b1 
      
 

a  b  a  (b)   a2    b2    a2    b2    a2  b2  .
 a   b   a   b   a  b 
 3  3  3  3  3 3
Übungen zu „Die Addition und die Subtraktion von Vektoren“
Buch Seite 24 Nr. 3 a, 4 a, Seite 30 Nr. 10 b 1), 2), 5), Nr. 13 a, c, Seite 32 Nr. 2 a,
Seite 33 Nr. 9, 11 a
3. Ermittle die folgenden Summen rechnerisch.
 5   2 
a)     
 4  1 
4. Berechne die folgenden Summen.
 5   6  1 
     
a)  1  [ 4    5 ]
 3   3   6 
     
10. Untersuche mit Hilfe des Satzes der Dreiecksungleichung, ob die gegebenen Vektoren
parallel sind und welche Orientierung sie gegebenenfalls haben. Bestätige das Ergebnis für
die Beispiele 1), 2) und 3) durch eine Zeichnung.
12  18 
6  9  3   4     
1)   ; 
 2)   ;   5)  4  ;  6 
 8   12   4   3   6   9 
   
13. Fällt man beim Aneinanderlegen von Pfeilen die Spitze des letzen Summanden mit dem
Anfang des ersten zusammen, so spricht man von einer geschlossenen Vektorkette.
a) Wie lautet der Summenvektor einer geschlossenen Vektorkette?
c) Durch welchen Vektor kann man eine offene Vektorkette zu a  b  c schließen?
2. Berechne a  b .
7 
 4 
11 
 
 
 
a)a   1 ; b   5  ; c   6 
3 
 1 
 4 
 
 
 
9. Die Pyramide wird durch drei Vektoren a, bund c aufgespannt. Drücke die zu den farbig
eingezeichneten Pfeile gehörenden Vektoren durch die gegebenen Vektoren aus.
11. Berechne die Koordinaten von x .
5 
 2
a)    x   
 2 
6
Lösungen:
3.
 5   2 
a)     
 4  1 
 5   2   5  (2)   3 
    
 
 4  1   4  1   5 
4.
 5   6   1 
     
a )  1  [ 4    5 ]
 3   3   6 
     
 5   6   1   5   6  1   5   5   5  5   0 
        
     
  
 1  [ 4    5 ]   1   4  (5)    1   1    1  1   2 
 3   3   6   3   3  6   3   3   3  3   6 
        
     
  
10.
b)
6  9 
1)   ; 
 | a  b || a |  | b |
 8   12 
| a | 6²  (8)²  36  64  100  10
| b | 9²  (12)²  81  144  225  15
 6   9   6  9  15 
ab   



 8   12   8  12   20 
| a  b | 15²  (20)²  225  400  625  25
| a  b || a |  | b | 10 15  25
Vektoren : Parallel !GleichOrientiert !
3   4 
2)   ;   | a  b || a |  | b |
 4   3 
| a | 3²  (4)²  9  16  25  5
| b | 4²  ( 3)²  16  9  25  5
3   4  3 4  7 
ab     
 
 4   3   4  3   7 
| a  b | 7²  (7)²  49  49  98
| a  b || a |  | b | 5  5  98 f . A
Vektoren : NICHTParallel ! NICHTGleichOrientiert !
12  18 
   
5)  4  ;  6  | a  b || a |  | b |
6  9 
   
| a | 12²  (4)²  6²  144  16  36  196  14
| b | 18²  ( 6)²  9²  324  36  81  441  21
12  18  12  18   30 
    
 

a  b   4    6    4  6    10 
 6   9   6  9  15 
    
 

| a  b | 30²  (10)²  15²  900  100  225  1225  35
| a  b || a |  | b | 14  21  35
Vektoren : Parallel !GleichOrientiert !
13.
a)a  b
c)a  b  c
2.
7 
 4 
11 
 
 
 
a )a  b; a   1 ; b   5  ; c   6 
3 
 1 
 4 
 
 
 
 7   4   7  4  11 
    
  
a  b   1   5    1  5    6 
 3   1   3  1   4 
    
  
9.
c1  a  b
d  a b
e  ac
f ag
g  c b
11.
5 
 2
a)    x   
 2 
6
5 
 2 5 
   x    |  
 2 
 6   2 
 2 5 
x    
 6   2 
 2  5   3 
x
 
 6  2 8 
 5   3   5  3   2 
    
 
 2   8   2  8   6 
Florian Modler