rrrrrrrrrrrrr eeeeeeeeeeee

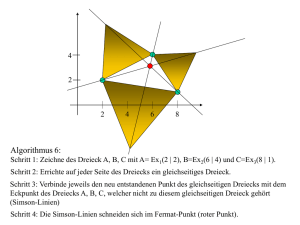
MaLa 2007 - Klasse 9
Geometrie
Wiederholung: Strahlensatze
Satz von Menelaos
Die Seiten eines Dreiecks ABC (oder deren Verlangerungen) werden von einer
Transversalen, die keine Ecktransversale ist, so in den Punkten D, E und F
geschnitten, wie in der Figur zu sehen ist. Dann gilt:
j
j
AD
DB
AA
jj
j j
BE
EC
jj j =1
j j j
CF
FA
A A F
A
C A
HH
HH A
HA E
H
A HH
A
HH
A
H
HH
A
A
D
B
Beweis durch einzeichnen einer geeigneten Hilfslinie (z.B. die Parallele zu AB
durch C , oder die Parallele zu DF durch A) und mehrfaches anwenden der
Strahlensatze.
Der analoge Satz gilt auch, wenn die schneidende Gerade keine der Dreiecksseiten, sondern nur alle 3 Verlangerungen schneidet. Der Beweis folgt auch analog.
Satz von Ceva
Seien C D, AE und BF drei Ecktransversalen eines Dreiecks ABC (wobei D
auf der Strecke AB , E auf der Strecke BC und F auf der Srecke AC liegt).
Dann gilt:
Die 3 Ecktransversalen C D, AE und BF schneiden sich genau dann in einem
Punkt, wenn gilt:
j
j
AD
DB
jj
j j
BE
EC
jj j =1
j j j
1
CF
FA
Beweis:
C
H
JJHH E
FP
HH
PP
JP
H
JPPP HH
PP H
J
PPH
J
PH
PH
PH
J
P
A
D
B
Wenn sich die 3 Ecktransversalen in einem Punkt P schneiden, dann kann man
die Gleichung auf verschiedene Weise durch mehrmaliges anwenden des Satzes
von Menelaos beweisen, z.B.:
Wendet man den Satz von Menelaos auf das Dreieck ABE mit der Transversalen
C D an, so folgt:
j
j
AD
DB
jj
j j
BC
CE
jj j =1
j j j
EP
PA
Wendet man den Satz von Menelaos auf das Dreieck AE C mit der Transversalen
F B an, so folgt:
j jj
j j j
AP
EB
PE
BC
jj j =1
j j j
CF
FA
Multipliziert man nun diese beiden Gleichungen, so erhalt man:
j
j
AD
DB
jj
j j
BE
EC
Damit ist die Hinrichtung gezeigt.
jj j =1
j j j
CF
FA
Zur Ruckrichtung:
Es gelte also:
j
j
AD
DB
jj
j j
BE
EC
jj j =1
j j j
CF
FA
Zeichnet man nun eine vierte Ecktransverale C D0 so ein, dass sie durch den
Schnittpunkt von AE und BF geht, so gilt fur diese Ecktransversalen nach der
Hinrichtung:
j
j
AD
0
0j
D B
Insbesondere also auch:
j
j
AD
DB
jj
BE
j
j=j
j j
EC
EC
BE
jj j =1
j j j
CF
FA
jj j=j
j j j j
0j
FA
AD
CF
D B
0
j
AX
Ein Punkt X im inneren einer Strecke AB ist aber durch das Verhaltnis XB
0
0
eindeutig bestimmt, d.h. die Punkte D und D stimmen uberein. Da C D durch
2
den Schnittpunkt von AE und BF geht, gilt also dasselbe fur C D. Die 3 Ecktransversalen schneiden sich also in einem Punkt.
Die Hinrichtung gilt auch noch, wenn die Ecktransversalen nicht die gegenuberliegende Seite, sondern nur deren Verlangerung schneiden.
Anwendnungen
Die einfachste Anwendung ist zu zeigen, dass sich die 3 Seitenhalbierenden eines
Dreiecks immer in einem Punkt schneiden.
Beweis dass sich die Winkelhalbierenden in einem Punkt schneiden mittels Satz
von Ceva. Dazu braucht man den folgenden Satz: Eine Ecktransversale C W
eines Dreiecks ABC (wobei W auf der Strecke AB liegt) ist genau dann eine
Winkelhalbierende des Dreiecks ABC , wenn
j
j
AW
WB
j=j j
j j j
AC
CB
gilt.
(Beweis dieses Satzes wieder mit geeigneter Hilfslinie, z.B. der Parallelen von
C W durch B und anwenden der Strahlens
atze und Winkel an geschnittenen
Parallelen)
Wiederholen der klassischen Beweise, dass sich die Mittelsenkrechten und die
Winkelhalbierenden eines Dreiecks immer in einem Punkt schneiden. (Mithilfe

geometrischer Orter)
Verbindet man die Beruhrungspunkte des Innkreises eines Dreiecks mit dessen
Seiten mit der gegenuberliegenden Ecke, so schneiden sich diese 3 Ecktransversalen in einem Punkt. (Beweis mit Satz von Ceva und Tangentenabschnitten)
Der Schwerpunkt teilt die Seitenhalbierenden im Verhaltnis 2:1. (Beweis mit
Satz von Menelaos)
Mittendreieck und Eulersche Gerade
Sei 4ABC ein beliebiges Dreieck, A0 der Mittelpunkt der Seite BC , B 0 der
Mittelpunkt der Seite AC und C 0 der Mittelpunkt der Seite AB . Dann ist
4A0B 0C 0 das Mittendreieck vom 4ABC .
Weiterhin sei S der Schnittpunkt der Seitenhalbierenden, H der Schnittpunkt
der Hohen und M der Schnittpunkt der Mittelsenkrechten im Dreieck ABC .
Nach der Umkehrung des ersten Strahlensatzes gilt: AB kA0 B 0 , C B kC 0 B 0 und
0 0
0 0
AC kA C . Auerdem folgt aus dem Strahlensatz: jAB j = 2 jA B j, jC B j =
2 jC 0 B 0 j und jAC j = 2 jA0 C 0 j. Insbesondere sind die Dreiecke ABC und
0 0 0 ahnlich und liegen in Ahnlichkeitslage.


A B C 
(Ahnlichkeitslage
bedeutet, dass
die sich entsprechenden Seiten parallel zueinander liegen)
Da der Schwerpunkt S die Seitenhalbierenden im Verhltnis 2:1 schneidet, geht
das Dreieck ABC aus dem Dreieck A0 B 0 C 0 durch Streckung um den Faktor 2
an S hervorgeht.
3
Die Mittelsenkrechten im Dreieck ABC entsprechen den Hohen im Dreieck
0 0 0
A B C . D.h. M ist der H
ohenschnittpunkt im Dreieck A0 B 0 C 0 . H geht also aus
M durch eine Streckung um den Faktor
2 an S hervor. D.h. M , S und H
liegen auf einer Geraden, welche die eulersche Gerade heit, und es gilt:
j
j
HS
SM
j=2
j 1
Beweis, dass sich die 3 Hohen in einem Punkt schneiden. (Man konstruiert
Parallelen zu den Seiten durch die Gegenuberliegenden Ecken und zeigt, dass
die Mittelsenkrechten in dem entstehenden groeren Dreieck die Hohen im ursprunglichen Dreieck sind)
Feuerbachscher Kreis (Neun-Punkte-Kreis)
In jedem Dreieck ABC liegen die 3 Seitenmitten, die 3 Hohenfupunkte und
die 3 Mittelpunkte der oberen Hohenabschnitte auf einem Kreis.
Zum Beweis:
Seien die Bezeichnungen wie eben und zusatzlich:
Ha ; Hb ; Hc die H
ohenfupunkte (Ha der gegenuber von A usw.)
O; P; R die Mittelpunkte der oberen H
ohenabschnitte (O auf AHa , P auf BHb
und R auf C Hc ) und
N der Mittelpunkt der Strecke jM H j.
Nach der Umkehrung des ersten Strahlensatzes gilt: OP kAB , P RkC B und
RO kAC . Auerdem folgt aus dem Strahlensatz: jAB j = 2 jOP j, jC B j = 2 jRP j
und jAC j = 2 jORj. Damit gilt auch: jOP j = jA0 B 0 j, jP Rj = jB 0 C 0 j und

jORj = jA0C 0j. Also liegen die Dreiecke OP R und A0B 0C 0 in Ahnlichkeitslage.
Daraus folgt leicht, dass sie durch eine Streckung um den Faktor 1 auseinander hervorgehen, was einer Drehung um 180 entspricht. Bei dieser Drehung
geht naturlich der Hohenschnittpunkt vom 4OP R (das ist H da die Hohen im
4ABC denen im 4OP R entsprechen) in den Hohenschnittpunkt vom 4A0B 0C 0
(das ist M ) uber. D.h. es handelt sich um eine Drehung um N (den Mittelpunkt
der Strecke jM H j).
Bei der Streckung, die 4A0 B 0 C 0 in 4ABC uberfuhrt, geht M in H und der
Umkreismittelpunkt vom 4A0 B 0 C 0 in M uber. Alle diese Punkte liegen auf
einer Geraden und mithilfe der Verhaltnisse der Streckung sieht man, dass der
Umkreismittelpunkt vom 4A0 B 0 C 0 auch der Mittelpunkt der Strecke jM H j also
N ist.
D.h. da 4OP R aus 4A0 B 0 C 0 durch Drehung um N hervorgeht liegen die Punkte A0 , B 0 , C 0 , O, P und R auf einem Kreis mit dem Mittelpunkt N . Mithilfe
der Umkehrung des Satzes von Thales sieht man leicht, dass auch Ha , Hb und
Hc auf diesem Kreis liegen.
4
Machtigkeit von Mengen
Es geht um die Frage, wann Mengen "Gleichgro" sind.
Bei endlichen Mengen ist das klar, aber wie sieht es mit unendlichen Mengen
aus?
Was stellt man sich intuitiv unter den groeren Mengen vor, wenn man die
naturlichen Zahlen, die geraden naturlichen Zahlen, die rationalen Zahlen und
die reellen Zahlen vergleicht?
Schon im endlichen stellt man fest, dass man beim Vergleichen von Mengen mit
Zuordnungen der Elemente arbeitet. Auch beim Zahlen ordnet man im Prinzip
jedem Element der zu zahlenden Menge eine Zahl zu. Weswegen es nahe liegt,
dass man sich mit Abbildungen und deren Eigenschaften beschaftigen muss.
Sei f : X
!
Y
eine Abbildung.
heit injektiv, wenn 2 verschiedene Elemente in X immer auf 2 verschiedene
Elemente in Y abbgebildet werden (oder: fur alle x; x0 2 X mit f (x) = f (x0 )
gilt: x = x0 ).
f
heit surjektiv, wenn jedes Element in Y mindestens ein Urbild in
d.h. fur jedes y 2 Y gibt es ein x 2 X mit f (x) = y .
f
f
X
hat,
heit bijektiv, wenn f injektiv und surjektiv ist.
Einfache Beispiele zu allen drei Begrien
Injektivitat und Surjektivitat hangen nicht nur von der Abbildungsvorschrift,
sondern auch von den Denitions- und Wertebereichen ab.
Es gibt noch eine andere Moglichkeit zu sagen, was bijektiv ist.
Eine Abbildung f : X ! Y ist genau dann bijektiv, wenn es eine Umkehrabbildung f 1 : Y ! X gibt (d.h. f f 1 = idY und f 1 f = idX )
Beweis:
Wenn f bijektiv ist, dann gibt es fur jedes y 2 Y genau ein x 2 X mit f (x) = y ,
dieses Element deniert man als f 1 (y ). Man sieht leicht, dass man auf diese
Weise die Umkehrabbildung deniert hat.
Wenn es eine Umkehrabbildung gibt, dann gilt:
Fur x; x0 2 X mit f (x) = f (x0 ) gilt auch:
x
= f 1 (f (x)) = f 1 (f (x0 )) = x0
ist also injektiv.
Fur jedes y 2 Y ist f 1 (y ) ein Urbild, d.h. f ist surjektiv, also auch bijektiv.
f
Im endlichen ist klar: Mengen haben gleichviele Elemente, wenn es eine bijektive
Abbildung zwischen ihnen gibt. Die verallgemeinerte Denition ist nun:
Zwei Mengen sind gleichmachtig, wenn es zwischen ihnen eine bijektive Abbildung gibt.
Eine unendliche Menge heit abzahlbar, wenn sie gleichmachtig zu den naturlichen Zahlen ist (sonst heit sie uberabzahlbar).
5
Die naturlichen Zahlen, die geraden naturlichen Zahlen, die ganzen Zahlen und
die rationalen Zahlen sind abzahlbar.
Die zugehorigen bijektiven Abbildungen sind:
N ! N : Identitat
N ! gerade Zahlen: hn 7 !n 2ni
f0g [ N ! Z: n 7 ! ( 1)2 n , wobei [] die Gauklammer ist.
N ist gleichmachtig zu f0g [ N.
Will man nun eine bijektive Abbildung von N nach Q konstruieren, so betrachtet man zunachst das folgende Diagramm, in dem jede positive rationale Zahl
mindestens einmal vorkommt:
1
1
2
1
3
1
4
1
1
2
2
2
3
2
4
2
1
3
2
3
3
3
4
3
..
.
..
.
..
.
..
.
...
Die Abbbildung geht nun die Diagonalen ab, wobei Zahlen, die schonmal vorkamen ubersprungen werden, d.h. die 1 wird auf 1 = 11 abgebildet, die 2 wird
auf 2, die 3 auf 12 , die 4 auf 3 und die 5 auf 13 abgebildet usw.
Das ist eine bijektive Abbildung zwischen den naturlichen Zahlen und den positiven rationalen Zahlen, aus der sich leicht eine bijektive Abbildung zwischen
N und Q konstruieren lasst.
D.h. die rationalen Zahlen sind abzahlbar.
Die reellen Zahlen sind nicht abzahlbar.
Beweis (Cantorsches Diagonalverfahren):
Angenommen es gabe eine bijektive Abbildung f von N nach R. Man schreibt
die Bilder in Dezimalschreibweise und konstruiert eine Zahl, die nicht im Bild
der Abbildung vorkommt. Diese Zahl beginnt mit 0; : : :. Die erste Nachkommastelle ist 1, wenn die erste Nachkommastelle von f (1) nicht 1 ist, sonst ist sie 2,
die zweite Nachkommastelle ist 1, wenn die zweite Nachkommastelle von f (2)
nicht 1 ist, sonst ist sie 2, usw.
Die so konstruierte Zahl ist nicht im Bild, denn sie stimmt mit dem Bild von
n in der n-ten Nachkommastelle nicht u
berein (fur alle n 2 N). Somit ist die
Abbildung nicht surjektiv, was ein Widerspruch ist, d.h. R ist nicht abzahlbar.
Hilberts Hotel
Ein Hotel habe unendlich viele Zimmer mit den Zimmernummern 1; 2; 3; : : : der
naturlichen Zahlen, die alle belegt sind. Wie kann man dennoch einen zu spat
kommenden Gast unterbringen?
Geht das auch mit abzahlbar unendlich vielen Gasten?
Und was ist, wenn noch abzahlbar unendlich viele Busse mit jeweils abzahlbar
unendlich vielen Menschen ankommen?
6