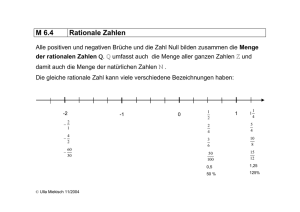
Die rationalen Zahlen

Die rationalen Zahlen
Caterina Montalto Monella
07.12.2016
1
1
Die Konstruktion der rationalen Zahlen
In dieser Ausarbeitung konstruieren wir die rationalen Zahlen aus den ganzen und den
natürlichen Zahlen. Dabei repräsentiert ein geordnetes Paar (p, n) mit p ∈ Z, n ∈ N die
rationale Zahl, die wir gewöhnlich als np schreiben. Somit stellen verschiedene geordnete
Paare die gleiche rationale Zahl dar, und für eine eindeutige Darstellung einer rationalen
Zahl denieren wir eine Relation zwischen diesen geordneten Paaren.
Denition 1. Seien (p, n) ∈ Z × N und (q, m) ∈ Z × N. Dann wird durch
(p, n) ≡ (q, m) :⇔ p × m = q × n.
eine Relation auf Z × N deniert.
Beispiel. Es gilt (−3, 5) ≡ (−6, 10), da −3 × 10 = −6 × 5 ist.
Bemerkungen. Sei (p, n) ∈ Z × N. Dann gelten folgende Aussagen.
1. Für alle k ∈ N ist (p, n) ≡ (kp, kn), da p × kn = kp × n gilt.
2. Falls p und n einen gemeinsamen Faktor haben, d.h. es gibt ein d ∈ N sowie (s, t) ∈
Z × N mit p = sd und n = td, so gilt die Relation
(p, n) ≡ (sd, td) ≡ (s, t).
3. Für p 6= 0 gibt es genau ein geordnetes Paar (s, t) ∈ Z × N mit (s, t) ≡ (p, n), sodass
s und t keinen gemeinsamen Faktor haben.
4. Wir schreiben nun pm statt p × m.
Satz 2. Die Relation ≡ ist eine Äquivalenzrelation auf Z × N, d.h. für alle (p,n) ∈ Z × N,
(q,m) ∈ Z × N und (r,l) ∈ Z × N gelten folgende Bedingungen.
1. Es gilt (p, n) ≡ (p, n) (Reexivität).
2. Mit (p, n) ≡ (q, m) folgt (q, m) ≡ (p, n) (Symmetrie).
3. Mit (p, n) ≡ (q, m) und (q, m) ≡ (r, l) folgt (p, n) ≡ (r, l) (Transitivität).
Beweis.
1. Es gilt pn = pn und somit (p, n) ≡ (p, n).
2. Sei (p, n) ≡ (q, m). Dann gilt pm = qn sowie qn = pm und somit (q, m) ≡ (p, n).
3. Es gilt
pm = qn,
ql = rm.
Nach Gleichung (1) gilt
(pm)l = (qn)l
und somit
(pl)m = n(ql).
2
(1)
(2)
Mit Gleichung (2) folgt nun
(pl)m = n(rm).
Da m 6= 0 ist, erhalten wir
pl = rn
und somit
(p, n) ≡ (r, l).
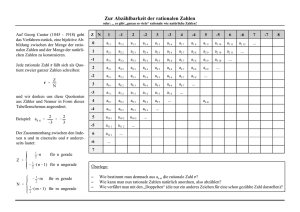
Denition 3. Die Menge Q := {[(p, n)]; (p, n) ∈ Z × N} ist die Menge aller Äquivalenz-
klassen unter der Äquivalenzrelation ≡ (siehe Abbildung 1). Die Elemente von Q heiÿen
rationale Zahlen.
Beispiel. Es gilt {(1, 2), (2, 4), (3, 6), ...} = [(1, 2)] ∈ Q.
(3, 6)
N
(2, 4)
(1, 2)
Z
Abbildung 1: Die Strahlen zeigen die Äquivalenzklassen von Z × N unter ≡.
Bemerkungen.
1. Eine rationale Zahl (p, n) ist positiv bzw. negativ, wenn p ∈ N bzw. −p ∈ N ist.
2. Eine rationale Zahl wird in vollständig gekürzter Form dargestellt, wenn sie
durch ein Paar (s, t) ∈ Z × N ohne gemeinsame Faktoren repräsentiert wird.
2
Die Arithmetik der rationalen Zahlen
Im Folgenden besprechen wir die Arithmetik der rationalen Zahlen und denieren dazu
zunächst die Addition und Multiplikation in Q.
3
Denition 4. Seien [(p, n)] ∈ Q und [(q, m)] ∈ Q. Dann ist die Addition + : Q×Q → Q
durch
[(p, n)] + [(q, m)] := [(pm + qn, nm)]
und die
Multiplikation × : Q × Q → Q durch
[(p, n)] × [(q, m)] := [(pq, nm)]
deniert.
Bemerkung. Die Addition und Multiplikation in Q sind abgeschlossen, da für m, n ∈ N,
p, q ∈ Z die Zahlen nm ∈ N, pq ∈ Z sowie (pm + qn) ∈ Z sind.
Lemma 5. Die Addition und Multiplikation in Q sind wohldeniert, d.h. sie sind unabhängig von der Wahl der Repräsentanten.
Beweis.
1. Wir zeigen, dass für (p, n), (p0 , n0 ), (q, m), (q 0 , m0 ) ∈ Z × N mit (p, n) ≡ (p0 , n0 ) und
(q, m) ≡ (q 0 , m0 ), auch (pm + qn, nm) ≡ (p0 m0 + q 0 n0 , n0 m0 ) gilt.
Seien (p, n), (p0 , n0 ), (q, m), (q 0 , m0 ) ∈ Z × N mit (p, n) ≡ (p0 , n0 ) sowie (q, m) ≡
(q 0 , m0 ), d.h. es gilt pn0 = p0 n und qm0 = q 0 m. Dann ist
(pm + qn)n0 m0 = pmn0 m0 + qnn0 m0
= p0 nmm0 + q 0 mnn0
= (p0 m0 )nm + (q 0 n0 )nm
= (p0 m0 + q 0 n0 )nm
und somit (pm + qn, nm) ≡ (p0 m0 + q 0 n0 , n0 m0 ).
2. Wir zeigen, dass für (p, n), (p0 , n0 ), (q, m), (q 0 , m0 ) ∈ Z × N mit (p, n) ≡ (p0 , n0 ) und
(q, m) ≡ (q 0 , m0 ), auch (pq, nm) ≡ (p0 q 0 , n0 m0 ) gilt.
Seien (p, n), (p0 , n0 ), (q, m), (q 0 , m0 ) ∈ Z × N mit (p, n) ≡ (p0 , n0 ) sowie (q, m) ≡
(q 0 , m0 ), d.h. es gilt pn0 = p0 n und qm0 = q 0 m. Durch Multiplizieren der beiden
Gleichungen erhalten wir
pn0 qm0 = p0 nq 0 m.
Daraus folgt
und somit gilt
pqn0 m0 = p0 q 0 nm
(pq, nm) ≡ (p0 q 0 , n0 m0 ).
Die folgenden Sätze für die Verknüpfungen + und × in Q können mit den Eigenschaften
von Z und Denition 4 bewiesen werden.
Satz 6. Die Addition und Multiplikation in Q sind jeweils kommutativ und assoziativ.
Für die Multiplikation gilt das Distributivgesetz.
Satz 7. Das neutrale Element der Addition in Q ist [(0, 1)]. Jedes [(p, n)] ∈ Q hat genau
ein inverses Element −[(p, n)] := [(−p, n)] bezüglich der Addition.
4
Satz 8. Das neutrale Element der Multiplikation in Q ist [(1, 1)].
Satz 9. Jede rationale Zahl auÿer [(0, 1)] hat ein inverses Element bezüglich der Multipli-
kation.
Beweis. Seien [(p, n)] ∈ Q und p ∈ N. Dann ist
[(p, n)] × [(n, p)] = [(pn, np)] = [(1, 1)],
[(n, p)] × [(p, n)] = [(np, pn)] = [(1, 1)]
und somit ist [(n, p)] das multiplikativ Inverse zu [(p, n)].
Sei [(p, n)] ∈ Q und p ∈ −N. Dann ist
[(p, n)] × [(−n, −p)] = [(−pn, −np)] = [(1, 1)],
[(−n, −p)] × [(p, n)] = [(−np, −pn)] = [(1, 1)]
und somit ist [(−n, −p)] das multiplikativ Inverse zu [(p, n)].
Bemerkung. Für p ∈ Z \ {0} hat [(p, n)] genau ein Inverses bezüglich der Multiplikation.
Satz 10. Die Division ist abgeschlossen in Q \ {[(0, 1)]}.
Denition 11. Eine Menge K zusammen mit zwei binären Verknüpfungen ⊕, ⊗ : K ×
K → K ist ein
Körper, falls
1. hK, ⊕i eine abelsche Gruppe ist,
2. hK \ {0}, ⊗i eine abelsche Gruppe ist,
3. ⊗ distributiv über ⊕ ist, d.h. es gilt
a ⊗ (b ⊕ c) = (a ⊗ b) ⊕ (a ⊗ c),
(a ⊕ b) ⊗ c = (a ⊗ c) ⊕ (b ⊗ c)
für a, b, c ∈ K .
Satz 12. Die Menge der rationalen Zahlen zusammen mit der Addition und Multiplikation
ist ein Körper.
Nun besprechen wir die Einbettung von Z in Q.
Lemma 13. Sei QZ ⊂ Q durch QZ := {[(p, n)] ∈ Q; n = 1} deniert. Dann ist durch
[(p, 1)] ↔ p eine Bijektion zwischen QZ und Z gegeben und es gilt
[(p, 1)] + [(q, 1)] = [(p + q, 1)],
[(p, 1)] × [(q, 1)] = [(pq, 1)].
Nun beschäftigen wir uns mit Potenzen in Q. Seien dazu a = [(p, q)] ∈ Q und n ∈ N. Dann
gelten für an , zusätzlich zu den Potenzgesetzen für die natürlichen Zahlen, die folgenden
Gesetze.
5
Satz 14. Für alle n ∈ N gilt
n
p
pn
= n.
q
q
Denition 15. Es gilt
a0 := 1.
Denition 16. Es gilt
a−n :=
1
.
an
Bemerkung. Die Umkehroperation zum Potenzieren heiÿt Radizieren. Mit der Denition für Umkehroperationen erhalten wir für a, c ∈ Q, n ∈ N die Identität
a=
√
n
c,
√
falls c = an gilt. Wenn n gerade ist, gilt (−a)n = an und n c ist die positive Lösung der
Gleichung c = an für gerade n 6= 0 (falls ein solches a ∈ Q existiert).
Denition 17. Es gilt
1
c n :=
falls
√
n
√
n
c,
c in Q existiert.
Korollar 18. Für alle p ∈ Z gilt
p
cn =
p
√
n
c .
Bemerkung. Radizieren in Q \ {0} ist nicht abgeschlossen.
3
Die Ordnung der rationalen Zahlen
Denition 19. Die rationale Zahl [(p, n)] ist gröÿer (>) als [(q, m)], wenn pm gröÿer als
qn ist. Die rationale Zahl [(p, n)] ist kleiner (<) als [(q, m)], wenn pm kleiner als qn ist.
Bemerkung. Insbesondere gilt [(a, c)] > [(b, c)] genau dann, wenn a > b ist. Für
[(p, n)], [(q, m)] ∈ Q mit pm > qn gilt also
pm
qn
q
p
=
>
= .
n
nm
nm
m
Beispiel. Wir bestimmen als Beispiel die Ordnung zwischen 53 und 11
.
19
Hier gilt 3 × 19 = 57 > 11 × 5 = 55 sowie
3
3 × 19
57
55
11 × 5
11
=
=
>
=
=
5
5 × 19
95
95
19 × 5
19
und somit ist
3
11
> .
5
19
Satz 20. Seien a, b, c ∈ Q. Dann gelten folgende Aussagen.
1. Für jedes a und b gilt entweder a < b, a = b oder b < a (Trichotomie).
6
2. Aus a < b und b < c folgt a < c (Transitivität).
3. Aus a < b folgt a + c < b + c (Verträglichkeit mit der Addition).
4. Aus a < b und 0 < c folgt ac < bc (Verträglichkeit mit der Multiplikation).
Bemerkung. Die in Satz 20 genannten Eigenschaften folgen aus den Eigenschaften der
Ordnung der ganzen Zahlen.
Satz 21. Die Menge der rationalen Zahlen ist dicht
geordnet, d.h. zwischen zwei ratio-
nalen Zahlen a und b mit b > a liegen unendlich viele weitere rationale Zahlen.
Beweis. Es genügt, die Existenz einer rationalen Zahl c zwischen a, b ∈ Q mit b > a zu
zeigen. Wir können c = 21 (a + b) wählen.
Satz 22. Nicht jede nach oben bzw. nach unten beschränkte Menge rationaler Zahlen hat
ein gröÿtes bzw. kleinstes Element.
Beispiel. Wir betrachten die Menge
Q+ := {a ∈ Q; a > 0} .
Diese ist nach unten beschränkt und 0 ist eine untere Schranke. Die Menge hat kein
kleinstes Element, da es für jedes l > 0 ein 2l ∈ Q+ mit 2l < l gibt.
Bemerkung. Nicht jede nach oben bzw. nach unten beschränkte Menge rationaler Zahlen
besitzt ein Supremum bzw. Inmum.
Beispiel. Sei
C := c ∈ Q; c2 < 3 ⊂ Q.
Dann ist C nach oben beschränkt, besitzt aber kein Supremum in Q.
Beweis. Wir zeigen, dass
UC := {q ∈ Q; c ≤ q für alle c ∈ C}
kein kleinstes Element besitzt.
Seien r > 0 das kleinste Element von UC und s =
3r+3
r+3
3r + 3
−r
r+3
3 − r2
=
r+3
. Dann ist
s−r =
(3)
und
3r + 32
−3
(r + 3)2
6(r2 − 3)
=
.
(r + 3)2
s2 − 3 =
7
(4)
Sei r2 < 3. Dann ist s2 < 3 nach Gleichung (4) und mit Gleichung (3) gilt s > r.
Damit gibt es ein s ∈ C mit s > r und somit folgt ein Widerspruch, dass r ∈
/ UC gilt.
Sei r2 > 3. Dann ist s2 > 3 nach Gleichung (4) und folglich s ∈ UC . Nun gilt s < r
nach Gleichung (3) und dies ist ein Widerspruch zur Voraussetzung.
Sei r2 = 3. Es existiert kein rationales r, das diese Gleichung erfüllt. Damit ist r ∈
/ UC
und es folgt ein Widerspruch.
8