Skript zur Vorlesung Statistik

Skript zur Vorlesung Statistik
Dietrich Baumgarten
«
2. April 2012
Inhaltsverzeichnis
1
Mengen, Zahlen und Funktionen
1
1.1
Mengen
1
1.2
Aussagen und Aussageformen
. . . . . . . . . . . . . . . . . . . . . . . .
2
1.3
Zahlenmengen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.3.1
Intervalle
4
1.3.2
Dezimalbruchentwicklung
. . . . . . . . . . . . . . . . . . . . . .
6
1.3.3
Teilbarkeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.3.4
Wissenschaftliche Darstellung einer Zahl
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . .
6
1.4
Mächtigkeit von Mengen . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.5
Relationen von Mengen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.6
Verknüpfungen von Mengen
1.6.1
. . . . . . . . . . . . . . . . . . . . . . . . .
9
Venn-Diagramme . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
1.7
Beispiele zu den Relationen und Verknüpfungen
. . . . . . . . . . . . . .
10
1.8
Zusammenfassung der Rechengesetze
1.9
Die Potenzmenge
. . . . . . . . . . . . . . . . . . . .
11
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.10 Kartesisches Produkt . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.10.1 Das kartesische Koordinatensystem
13
. . . . . . . . . . . . . . . . .
15
1.11 Relationen und Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . .
15
1.12 Funktionen
1.12.1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
Hintereinanderausführung von Funktionen . . . . . . . . . . . . .
19
1.13 Spezielle Eigenschaften mancher Funktionen
. . . . . . . . . . . . . . . .
19
iii
Abbildungsverzeichnis
1.1
Die Zahlengerade
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2
Venn-Diagramme
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3
Die Potenzmenge von x, y, z als Hasse-Diagramm
1.4
Das kartesische Koordinatensystem
1.5
Kartesisches Produkt, Relationen und Funktionen
. . . . . . . . . . . .
16
1.6
Graph einer reellen Funktion . . . . . . . . . . . . . . . . . . . . . . . . .
18
1.7
Bijektive Funktion und Inverse . . . . . . . . . . . . . . . . . . . . . . . .
21
10
. . . . . . . . . . . . .
13
. . . . . . . . . . . . . . . . . . . . .
15
v
Tabellenverzeichnis
1.1
Rechengesetze für Mengenoperationen . . . . . . . . . . . . . . . . . . . .
11
vii
1 Mengen, Zahlen und Funktionen
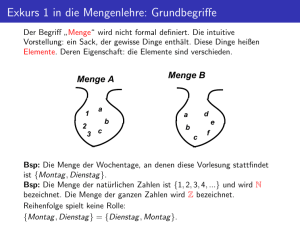
In der Mathematik bildet das Konzept der
Menge
die Grundlage einer einheitlichen,
knappen und anschaulichen Beschreibung von Objekten, die durch eine gemeinsame Eigenschaft zusammengehören. Diese Objekte heiÿen Elemente der Menge. Der Mengenbegri ist grundlegend für alle Zweige der Mathematik und erleichtert die mathematische
Modellbildung. Für die Untersuchung von Mengen werden bestimmte Begrie und Operationen eingeführt und daraus Gesetzmäÿigkeiten hergeleitet, die man als Mengenlehre
bezeichnet.
1.1 Mengen
Die Mengenlehre wurde von den Mathematikern Georg Cantor und Richard Dedekind
entwickelt. Die Denition von Georg Cantor lautet wie folgt:
Denition 1.1. Eine Menge ist eine Zusammenfassung bestimmter wohlunterschiedener
Objekte unserer Anschauung oder unseres Denkens, welche die Elemente der Menge
genannt werden, zu einem Ganzen.
Diese Denition ist nicht widerspruchsfrei und führt zu Paradoxien wie die Menge
aller Mengen, die sich selbst als Element enthalten müsste. Trotzdem ist diese Denition
ausreichend für ein solides Fundament der meisten Zweige der Mathematik. Eine Menge
kann nur dann verwendet werden, wenn es eine klare Entscheidung darüber gibt, ob ein
bestimmtes Element zu ihr gehört oder nicht. Mengen werden auf zwei Weisen gebildet,
und zwar entweder durch
Aufzählung
oder durch eine
Beschreibung
der Elemente. Das
wird jetzt genauer festgehalten:
ˆ
Mengen werden meistens mit groÿen Buchstaben und die Elemente mit kleinen
Buchstaben bezeichnet.
ˆ
Die Zugehörigkeit eines Elementes
ˆ
Beim aufzählenden Verfahren stehen die Elemente in einer geschweiften Klammer
x zu einer Menge M wird durch das Symbol ∈
angezeigt, also x ∈ M . Durch y ∈
/ M wird ausgedrückt, dass y kein Element der
Menge M ist. Sei etwa V die Menge aller Vokale, so gelten a ∈ V und b ∈
/ V.
und sind durch Komma getrennt, wie etwa die Menge
ˆ
M = { 2,
5, 7 }.
Bei unendlichen Mengen werden einige Elemente angegeben, die das Bildungsgesetz
zeigen und der Rest durch drei Pünktchen angedeutet, wie etwa die Menge der
natürlichen Zahlen
N = { 1, 2, 3, 4, . . . }.
1
1 Mengen, Zahlen und Funktionen
ˆ
Beim beschreibenden Verfahren geht man von einer bereits denierten Menge aus
und schränkt nach einem Längsstrich die Elemente durch eine Eigenschaft ein wie
etwa
M = {x ∈ N | x
ist Primzahl }.
Mengen dürfen aus beliebigen Elementen bestehen wie etwa
K = { CDU, 3,
Hut }, erge-
ben sich aber meistens durch gemeinsame Eigenschaften der Elemente. Die Buchstaben
M = { S, T, A, I, K }. Die Elemente der
Menge M könnte, muss aber nicht in der geord-
des Wortes STATISTIK bilden die Menge
Menge müssen nicht geordnet sein, die
neten Weise
M = { A,
I, K, S, T } geschrieben werden. Auÿerdem wird jedes Element
einer Menge nur einmal aufgeführt. Eine besondere Rolle spielt die sogenannte leere
Menge, die keine Elemente hat, daher die Beschreibung leer. Die leere Menge wird mit
{}
oder mit
∅
gekennzeichnet. Die leere Menge ist nicht immer sofort zu erkennen und
tarnt sich beispielsweise wie folgt:
L = { x ∈ R | x2 + 1 = 0 }.
Hier soll
L
die Menge aller reelle Lösungen der Gleichung
x2 + 1 = 0
sein, die aber
leer ist, da die Gleichung keine reellen Lösungen hat. Die Einführung der leeren Menge
ermöglicht es also Mengen zu beschreiben, die möglicherweise gar keine Elemente haben,
d.h. man muss diesen Fall nicht als Sonderfall ausschlieÿen, da auch die leere Menge als
Menge gilt.
1.2 Aussagen und Aussageformen
Eine
Aussage A
ist die Darstellung eines Sachverhalts, der entweder wahr oder falsch
ist. Enthält die Aussage mindestens eine Variable wie
sageform A(x).
x,
so spricht man von einer
Aus-
Der Satz Die USA haben mehr Einwohner als China ist eine Aussage, da man
die Richtigkeit nach allgemein anerkannten Verfahren entscheiden kann. Der Satz Die
Regierung der USA ist mehr um das wohl der Menschheit bemüht als die Regierung von
China ist keine Aussage, da man die Richtigkeit nur dann überprüfen könnte, wenn
allgemein gültige Kriterien für das Kümmern um das Wohl der Menschheit vorlägen.
2
Eine Aussageform ist etwa: A(x) : x ≥ x, x ∈ N. Setzt man an die Stelle der Variablen
einen Wert wie
x = 1
ein, so entsteht eine Aussage. Mengen werden sehr oft durch
Aussageformen festgelegt, etwa
M = { x ∈ N | x2 > x }.
Diese Menge besteht aus allen natürlichen Zahlen
ist, also aus der Menge
Eine Aussage
wahr, wenn
A
A
A
man die Operatoren
2
wofür die Aussageform
A(x)
wahr
N \ { 1 }.
kann negiert werden. Die Negation wird mit
falsch ist und falsch, wenn
Zwei Aussagen
x,
A
¬A
bezeichnet. Sie ist
wahr ist.
und B können durch und und oder verknüpft werden, wofür
∧ und ∨ verwendet. Die Aussage C = A ∧ B ist wahr, wenn sowohl
1.3 Zahlenmengen
A
als auch
oder
B
B
wahr sind, und sonst falsch. Die Aussage
D = A∨B
ist wahr, wenn
A
oder beide wahr sind, und sonst falsch, d.h mindestens eine der beiden Aussagen
muss wahr sein. Die logischen Operatoren
Daneben gibt es noch den
Allquantor ∀
¬, ∧
und
und den
x
steht bei Aussageformen anstelle von Für alle
steht für Es gibt ein
x,
wofür
A(x)
Quantoren genannt.
Existenzquantor ∃. Der Allquantor
∨
gilt
werden
A(x)
und der Existenzquantor
gilt. Durch die beiden letzten Quantoren werden
Aussageformen oft zu einfachen Aussagen.
Beispiel 1.1.
Die Aussageform
A(x) : x2 > x
wird durch den Allquantor zu einer
Aussage
∀x ∈ N
gilt
A(x),
was eine falsche Aussage ist, da die Aussageform für
x=1
falsch ist. Dagegen ist die
Aussage
∃x ∈ N
x = 1 tatsächlich
¬A(x) richtig.
richtig weil es mit
ist, und damit
mit
¬A(x)
einen Wert gibt, für den die Aussage
A(x)
falsch
1.3 Zahlenmengen
Die wichtigsten Mengen sind Zahlenmengen wie die Menge der natürlichen Zahlen
Zahlenmengen werden auf der sogenannten
Zahlengeraden
N.
veranschaulicht. Darauf wer-
den willkürlich zwei Punkte gewählt, der linke repräsentiert die Zahl 0, der rechte die
Zahl 1, der Abstand zwischen beiden Punkten wird ebenfalls als 1 bezeichnet. Die nächste natürliche Zahl 2 liegt rechts von der 1 im Abstand 1. Hängt man nach diesem Prinzip
an die jeweils zuletzt erzeugte natürliche Zahl
sich die nächste natürliche Zahl
n
nach rechts den Abstand 1 an, ergibt
n+1. Dieser Vorgang kann unendlich oft wiederholt wer-
den, also gibt es unendlich viele natürliche Zahlen und die Zahlengerade ist nach rechts
unendlich lang. Wie bei einem Thermometer werden die negativen ganzen Zahlen spiegelbildlich zur Zahl 0 abgetragen, d.h. für
0 den Abstand
n. Auf
n∈N
−n links von der
Z = { 0, 1, −1, 2, −2, 3, −3, . . . }
hat die negative Zahl
diese Weise ergibt sich die Menge
der ganzen Zahlen. Wie bei vielen unendlichen Mengen verwendet man auch hier drei
Punkte
...
um anzudeuten, dass es immer so weiter geht. Die Zahlengerade ist nach
rechts und links unbeschränkt, was durch je einen Pfeil links und rechts angedeutet
wird.
Der Doppelstrich wird für alle wichtigen Zahlenmengen benutzt, wie auch für die Menge der rationalen Zahlen
wird, wobei
q 6= 0
Q,
die durch Brüche
p/q
von ganzen Zahlen
p
und
q
gebildet
gelten muss. Die rationalen Zahlen liegen so dicht verpackt auf der
Zahlengeraden, dass zwischen je zwei rationale Zahlen immer noch unendlich viele weitere rationale Zahlen liegen. Trotzdem füllen die rationalen Zahlen die Zahlengerade nicht
√
aus, es bleiben Lücken wie etwa für die Zahl
Zahlen dieser Art werden als
irrational
2, die man nicht als Bruch darstellen kann.
bezeichnet. Die irrationalen Zahlen ergänzen die
rationalen Zahlen zur Menge der reellen Zahlen
R,
womit dann alle Punkte der Zahlen-
geraden erfasst sind. Zwei Zahlen mit gleichem Abstand von der Zahl 0 unterscheiden
3
1 Mengen, Zahlen und Funktionen
sich jeweils nur im Vorzeichen, wie etwa 1 und -1, zwei derartige Zahlen nennt man
genzahlen
Betrag . Der Betrag wird
und ihren Abstand zum Nullpunkt den (absoluten)
durch zwei Striche symbolisiert, etwa
| − 2, 1| = 2, 1 = |2, 1|.
Ge-
Der Betrag einer positiven
Zahl ist stets die Zahl selbst, der Betrag einer negativen Zahl
x
ist gleich
−x.
In der Abbildung 1.1 sehen Sie die Zahlengerade und drei besonders berühmte irrationale Zahlen mit ihren Gegenzahlen, nämlich
und
√
2 = 1, 41421356 . . ., e = 2, 71828182 . . .
π = 3, 14159265 . . .
-π -e
-√2
√2
-4 -3,5 -3 -2,5 -2 -1,5 -1 -0,5 0
0,5
1
1,5
e π
2
2,5
3
3,5
4
Abbildung 1.1: Die Zahlengerade
1.3.1 Intervalle
Intervalle sind zusammenhängende Teilmengen von
durch seine untere Grenze
a
und seine obere Grenze
R. Ein beschränktes Intervall wird
b festgelegt, wobei jede der beiden
Grenzen zum Intervall gehören darf, aber auch ausgeschlossen sein kann. Es gibt also
vier Formen von beschränkten Intervallen. Ein beschränktes Intervall ist
abgeschlossen ,
oen , wenn beide Grenzen nicht enthalten
sind. Ein beschränktes Intervall heiÿt links halboen , wenn a nicht dazu gehört, aber b
doch. Ein beschränktes Intervall heiÿt rechts halboen , wenn b nicht dazu gehört, aber
wenn es beide Grenzen
a
a
und
b
enthält, und
doch.
Man verwendet für Grenzen, die zum Intervall gehören, eckige Klammern und runde
Klammern für Grenzen, die nicht zum Intervall gehören. Statt der runden Klammern
werden auch nach auÿen gewendete (gespiegelte) eckige verwendet. Im Folgenden werden
beide Schreibweisen gezeigt und der Mengenschreibweise gegenübergestellt:
ˆ
Abgeschlossenes Intervall (enthält
a
und
b):
[a, b] = { x ∈ R | a ≤ x ≤ b }.
ˆ
Oenes Intervall (enthält weder
a
noch
b):
(a, b) =]a, b[= { x ∈ R | a < x < b }.
ˆ
Linksoenes Intervall (enthält nicht
a,
aber
b):
(a, b] =]a, b] = { x ∈ R | a < x ≤ b }.
4
1.3 Zahlenmengen
ˆ
Rechtsoenes Intervall (enthält nicht
b,
aber
a):
[a, b) = [a, b[= { x ∈ R | a ≤ x < b }.
Es wird auch der Fall zugelassen, dass ein Intervall nach links oder rechts unbeschränkt
ist. Bei nach rechts unbeschränkten Intervallen fehlt die Obergrenze
b.
Die gewohnte
b = ∞ gesetzt wird. EntIntervall a = −∞ gesetzt. Wieder
Schreibweise kann beibehalten werden, wenn in diesem Fall
sprechend wird bei einem nach links unbeschränkten
gibt es vier mögliche unbeschränkte Intervalle:
ˆ
Rechtsseitig unendliches abgeschlossenes Intervall (enthält
a):
[a, ∞) = [a, ∞[= { x ∈ R | a ≤ x < ∞ }.
ˆ
Rechtsseitig unendliches oenes Intervall (enthält
a
nicht):
(a, ∞) =]a, ∞[= { x ∈ R | a < x < ∞ }.
ˆ
Linksseitig unendliches abgeschlossenes Intervall (enthält
b):
(−∞, b] =] − ∞, b] = { x ∈ R | −∞ < x ≤ b }.
ˆ
Linksseitig unendliches oenes Intervall (enthält
b
nicht):
(−∞, b) =] − ∞, b[= { x ∈ R | −∞ < x < b }.
Zur Vermeidung von Verwechslungen mit dem Dezimalkomma wird als Trennzeichen
manchmal das Semikolon (;) verwendet.
Beispiel 1.2.
ˆ [2, 3]:
Ich gebe jetzt einige Beispiele von Intervallen an.
alle reellen Zahlen zwischen 2 und 3, einschlieÿlich von 2 und 3.
ˆ (2, ∞):
alle reellen Zahlen, die echt gröÿer als 2 sind.
ˆ [2, ∞):
alle reellen Zahlen, die gröÿer gleich 2 sind.
ˆ [2, 3; 3, 3]:
alle reellen Zahlen zwischen 2,3 und 3,3, einschlieÿlich von 2,3 und 3,3.
ˆ (2, 3; 3, 3]:
alle reellen Zahlen zwischen 2,3 und 3,3, ohne 2,3, aber mit 3,3.
5
1 Mengen, Zahlen und Funktionen
1.3.2 Dezimalbruchentwicklung
Mit Hilfe der
Dezimalbruchentwicklung kann man jeder reellen Zahl eine Folge von Ziern
in der Form
±zm zm−1 . . . z0 , z−1 z−2 . . . z−n . . .
(m ∈ N zi ∈ {0, . . . , 9})
zuordnen. Bei einer beliebigen reellen Zahl bricht die Folge nach dem Komma nicht ab.
Der Wert der Dezimalbruchentwicklung ist
Z=±
−∞
X
zi · 10i .
i=m
z−k = 0 für ∀k > n gilt, spricht
p/q mit q 6= 0 ist genau dann ein
Wenn die Folge nach dem Komma endlich ist, also
man von einem
Dezimalbruch .
Dezimalbruch, wenn
q
Eine rationale Zahl
das Produkt ist von Faktoren, die nur die Werte 2 oder 5 haben.
Man kann q dann zu einer Potenz von 10 erweitern. Sei etwa r = 3/40, so ist 40
23 · 5, man muss also Zähler und Nenner mit 25 = 52 erweitern und erhält r = 3/40
75/1000 = 0, 075.
Wenn q die genannte
Bedingung nicht erfüllt, ergibt sich für
p/q
=
=
eine periodische De-
zimalbruchentwicklung, d.h. eine Zier oder eine Folge von Ziern wiederholen sich nach
dem Komma unendlich oft. Alle rationalen Zahlen, und nur diese, haben eine periodische Dezimalbruchentwicklung. Man unterscheidet rein periodische Dezimalbrüche, bei
denen die Periode sofort nach dem Komma beginnt, wie etwa 0,1111. . . und gemischt periodische Dezimalbrüche, bei denen nach dem Komma zunächst eine Vorperiode steht,
bevor die Periode beginnt, etwa 0,2313131. . . . Anstatt der drei Pünktchen werden die
Perioden durch einen Überstrich angedeutet, also
0, 142857
oder
0, 231.
1.3.3 Teilbarkeit
Bei natürlichen Zahlen spielt die Teilbarkeit eine groÿe Rolle. Man nennt eine natürliche
q
Teiler
q ohne Rest teilbar ist. Man
schreibt dann q|n und sagt n ist durch q teilbar oder q teilt n. Für 5|10 kann man sagen:
Zahl
einen
der natürlichen Zahl
n,
wenn
n
durch
5 teilt 10< oder 10 ist durch 5 teilbar<. Wenn zwei Zahlen nur den trivialen Teiler
1 gemeinsam haben, werden sie
Jede natürliche Zahl
n
teilerfremd
genannt, wie etwa 10 und 21.
hat zwei triviale Teiler, nämlich 1 und die Zahl selbst. Alle
anderen Teiler werden echte Teiler genannt. Die Menge aller Teiler einer natürlichen
Zahl
n
wird mit
T (n)
bezeichnet, somit ist etwa
Eine natürliche Zahl
p
heiÿt
Primzahl ,
T (4) = { 1, 2, 4 }.
wenn sie nur durch 1 und durch sich selbst
teilbar ist, wobei die 1 selbst nicht als Primzahl gilt. Somit sind die Primzahlen alle
Zahlen mit genau zwei Teilern.
1.3.4 Wissenschaftliche Darstellung einer Zahl
Bei sehr groÿen oder sehr kleinen Zahlen wird häug die sogenannte wissenschaftliche
Darstellung einer Zahl verwendet. Dabei wird eine Zahl durch eine Mantisse und eine
6
1.4 Mächtigkeit von Mengen
Potenz von 10 dargestellt, wobei die Mantisse genau eine Stelle vor dem Komma hat
n
6
und statt 10 der Ausdruck En verwendet wird, etwa 1, 23 E 6, womit die Zahl 1, 23 · 10
gemeint ist. Für die normale Darstellung wird das Komma in der Mantisse um so viele
Stellen nach rechts verschoben, wie der Exponent angibt, wobei leeren Stellen zuvor mit
Nullen auüllen zu sind. Somit gilt
1, 23 E 6 = 1, 230000 E 6 = 1, 230000 106 = 1.230.000.
Umgekehrt lautet wissenschaftliche Darstellung von 12345678 somit
1, 2345678 E 7,
da
das Komma um sieben Stellen nach rechts verschoben wurde.
Bei sehr kleinen Zahlen werden negative Zehnerpotenzen eingesetzt, aber die Mantisse
hat auch jetzt genau eine Stelle vor dem Dezimalkomma. Für die normale Darstellung
werden bei einem negativen Exponenten
E −n
nach dem Komma
n−1
Nullen gesetzt
und dann folgen ohne Komma die Ziern der Mantisse. Somit gilt
1, 23 E −6 = 0, 00000123.
Hier sind
5 = 6 − 1 Nullen nach dem Komma nötig, dann folgen die Ziern der Mantisse.
Umgekehrt sucht man bei der normalen Darstellung die erste von 0 verschiedene Zier
und nennt die Stellenzahl
n.
Die Mantisse wird von den Ziern ab der Stelle
n
gebildet,
wobei die Zier der n-ten Stelle vor dem Komma steht. Somit lautet die wissenschaftliche
Darstellung von 0,00000001234 somit
1, 224 E −8,
da die erste von 0 verschiedene Zier
an der achten Stelle steht.
In der wissenschaftlichen Darstellung lassen sich Zahlen leicht miteinander multiplizieren und dividieren, und zwar werden beim Multiplizieren die beiden Mantissen miteinander multipliziert und die Exponenten addiert, während man beim Dividieren die
beiden Mantissen dividiert und die Exponenten subtrahiert.
1, 2 E −6 · 2, 345 E 8 = 2, 814 E 2
1, 2 E −6 : 2, 345 E 8 = 0, 511727079 E −14 = 5, 11727079 E −15
1.4 Mächtigkeit von Mengen
Denition 1.2.
Unter der Mächtigkeit einer endlichen Menge
Anzahl ihrer Elemente. Man schreibt dafür
M
versteht man die
|M |.
Die Mächtigkeit der leeren Menge wird 0 gesetzt, da sie kein Element hat. Bei allen
nicht leeren endlichen Mengen ist die Mächtigkeit eine natürliche Zahl. Die Menge
{ 1, 2, 3 }
hat die Mächtigkeit
Denition 1.3.
Zwei Mengen
wenn jedem Element von
ein Element von
A
A
A=
|A| = 3.
A
und
B
(A ∼ B),
von B genau
heiÿen gleichmächtig, symbolisch
genau ein Element von
B
und jedem Element
zugeordnet werden kann.
7
1 Mengen, Zahlen und Funktionen
Zwei endliche Mengen
A und B
sind genau dann gleich mächtig, wenn sie dieselbe An-
zahl von Elementen besitzen, also
und
B = { a, b, c }
|A| = |B|
A = { 1, 2, 3 }
C = { 1, 2 }. Bei endli-
gilt. Somit sind die Mengen
A
gleich mächtig, nicht aber die Mengen
und
chen Mengen kann eine echte Teilmenge niemals so mächtig sein wie ihre Obermenge, bei
unendlichen Mengen ist das erstaunlicherweise schon möglich. Seien dazu die Mengen
N
der natürlichen Zahlen und die Menge
Obwohl
G
eine echte Teilmenge von
Element von
N
N
G
der geraden natürlichen Zahlen betrachtet.
ist, kann man jedem Element von
zuordnen, und zwar über die Vorschrift
G
genau ein
n ↔ 2n.
Mengen mit gleicher Mächtigkeit wie die natürlichen Zahlen sind in der Mathematik
besonders wichtig, da sie die einfachsten nicht endlichen Mengen sind. Man führt für
diese Mengen einen eigenen Begri ein.
Denition 1.4. Eine Menge A heiÿt abzählbar, wenn sie endlich oder gleichmächtig zur
Menge
N der natürlichen Zahlen ist. Nicht endliche abzählbare Mengen werden abzählbar
unendlich genannt.
1.5 Relationen von Mengen
Wie für Zahlen gibt es auch für Mengen bestimmte Beziehungen, die man durch Operatoren knapp und zweckmäÿig beschreiben kann. Zunächst wird untersucht, wie man
Mengen vergleichen kann.
(1) Gleichheit
A = B.
Die einfachste Beziehung zwischen zwei Mengen
A
und
B
ist die Gleichheit, die
genau dann gilt, wenn beide Mengen dieselben Elemente enthalten. Man drückt dies
durch den Operator
=
aus. Zum Beispiel gilt
{ 1, 2, 3 } = { 3, 1, 2 },
da bei Mengen
die Reihenfolge der Elemente keine Rolle spielt.
A 6= B .
Mengen A
(2) Ungleichheit
Wenn zwei
(3)
B nicht
A 6= B
und
Man schreibt dafür kurz
gleich sind, werden sie als ungleich bezeichnet.
B , A ⊆ B bzw. B ⊇ A.
A als Teilmenge der Menge B , wenn jedes Element der
Menge A auch Element der Menge B ist. Der entsprechende Operator ist ⊆. Wenn
A eine Teilmenge von B ist, nennt man B die Obermenge von A. Die leere Menge
∅ ist Teilmenge jeder Menge A und jede Menge A ist Teilmenge von sich selbst also
ausgedrückt durch Operatoren ∅ ⊆ A und A ⊆ A.
A
ist Teilmenge von
Man bezeichnet eine Menge
(4)
A
ist echte Teilmenge von
Man nennt
mit
B
A
eine
B, A ⊂ B
echte Teilmenge
B ⊃ A.
B , wenn A
bzw.
von
Teilmenge von
übereinstimmt. Der entsprechende Operator ist
B
ist, aber nicht
⊂. Die Menge aller Vokale ist
eine echte Teilmenge der Menge aller Buchstaben und die Menge aller Primzahlen
eine echte Teilmenge von
8
N.
1.6 Verknüpfungen von Mengen
1.6 Verknüpfungen von Mengen
Aus Grundmengen
A und B
lassen sich weitere Mengen bilden, auch für die Darstellung
dieser Verknüpfungen werden Operatoren verwendet.
A ∩ B.
(1) Durchschnitt von Mengen
A und B ist die Menge aller Elemente, die sowohl
A als auch zur Menge B gehören. Die Durchschnittsmenge wird mit A∩B
Der Durchschnitt zweier Mengen
zur Menge
gekennzeichnet. Somit gilt
A ∩ B = {x | x ∈ A
Daher ist der Durchschnitt von
B,
A
und
B
und
x ∈ B }.
A
eine Teilmenge sowohl von
als auch von
also
A ∩ B ⊆ A,
A ∩ B ⊆ B.
A ∩ B = B ∩ A. Auch
Die Durchschnittsbildung kann vertauscht werden, d.h. es gilt
wenn man den Durchschnitt von mehr als zwei Mengen bildet, spielt die Reihenfolge
keine Rolle. Haben zwei Mengen
A und B
kein gemeinsames Element, so nennt man
sie elementfremd (disjunkt), die Durchschnittsmenge ist dann die leere Menge, also
sind
A
und
B
genau dann disjunkt, wenn
eine Teilmenge von
B,
wenn
A∩B =A
A ∪ B.
A
(2) Vereinigung von Mengen
Die Vereinigung zweier Mengen
A genau
A ∩ A = A.
gilt. Weiter ist
ist. Insbesondere gilt
B
und
A∩B =∅
dann
ist die Menge aller Elemente, die zu einer
der beiden Mengen gehören. Selbstverständlich schlieÿt dies auch die Elemente mit
ein, die zu beiden Mengen, also dem Durchschnitt gehören. Die Vereinigungsmenge
wird mit
A∪B
gekennzeichnet. Somit gilt
A ∪ B = {x | x ∈ A
Somit sind beide Mengen
A
und
B
oder
x ∈ B }.
Teilmenge ihrer Vereinigung, also
A ⊆ A ∪ B,
B ⊆ A ∪ B.
Die Vereinigungsbildung kann vertauscht werden, d.h. es gilt
A ∪ B = B ∪ A.
Auch
wenn man die Vereinigung von mehr als zwei Mengen bildet, spielt die Reihenfolge
A genau
A ∪ A = A.
keine Rolle. Weiter ist
Insbesondere gilt
dann eine Teilmenge von
B,
wenn
A∪B = B
ist.
A\B
Die Dierenzmenge A \ B ist die Menge aller Elemente von A, die nicht zu B gehören.
(3) Die Dierenzmenge
Somit gilt
A\B = {x | x ∈ A
Die Dierenzmenge
dann mit
A
A\B
überein, wenn
und
x∈
/ B }.
ist natürlich eine Teilmenge von
A
und
B
A
und stimmt genau
disjunkt sind. Die Dierenzmenge
dagegen genau dann die leere Menge, wenn
A
eine Teilmenge von
B
A\B
ist
ist.
9
1 Mengen, Zahlen und Funktionen
(4) Die Komplementärmenge
Ā.
Fast immer sind Mengen Teilmengen einer Grundmenge, die in der Statistik meist
Ω
heiÿt. Die Komplementärmenge
Ā
ist dann gleich
Ā = { x | x ∈ Ω
Ω \ A.
und
x∈
/ A }.
Ac
oder mit
Die Komplementärmenge wird oft auch mit
Somit gilt
A0
bezeichnet.
1.6.1 Venn-Diagramme
Die vier Verknüpfungen lassen sich grasch durch sogenannte Venn-Diagramme veranschaulichen. Das äuÿere Rechteck stellt die Grundmenge
die Mengen
A
und
A
Ω
dar, die inneren Rechtecke
B.
B
A
B
(a) A∩B
A
B
(b) AUB
A
(d) Ac
(c) A\B
Abbildung 1.2: Venn-Diagramme
1.7 Beispiele zu den Relationen und Verknüpfungen
Im folgenden Beispiel wird als Grundmenge
G, U
angenommen. Weiter seien mit
und
P
Ω
die Menge der Primzahlen bezeichnet. Die Menge
12, also die Menge
{ 2, 3, 4, 6 }.
ist das Komplement von
ˆ N
ist die Vereinigung von
Die leere Menge
ˆ
Der Durchschnitt von
∅
U,
G
also
T (12)
bezeichne die echten Teiler von
und
G = Ū = N \ U .
U,
also
N = G ∪ U.
ist der Durchschnitt von
G
N
Es gelten dann u.a. folgende Beziehungen.
ˆ G
ˆ
die Menge der natürlichen Zahlen
die Menge der geraden und ungeraden sowie
und
P
G
ist die Menge
und
U,
{ 2 },
also
∅ = G ∩ U.
{ 2 } = P ∩ G,
da 2 die
U ∪ P = { 2, 3, 5, 7, . . . },
also alle
also
einzige gerade Primzahl ist.
ˆ
Die Vereinigung von
U
und
P
ist die Menge
ungeraden Zahlen und die Zahl 2, da 2 die einzige gerade Primzahl ist.
10
1.8 Zusammenfassung der Rechengesetze
ˆ
Der Durchschnitt von
ˆ
Der Dierenz von
P
P
und
und
T (12)
T (12)
ist die Menge
P ∩ T (12) = { 2, 3 }.
ist die Menge
P \ T (12) = { x ∈ P | x ≥ 5 }.
1.8 Zusammenfassung der Rechengesetze
In der folgenden Tabelle werden die wichtigsten Gesetzmäÿigkeiten für das Rechnen mit
Mengen zusammengefasst.
Tabelle 1.1: Rechengesetze für Mengenoperationen
Gesetz
∩
∪
Idempotenz
A∩A=A
(A ∩ B) ∩ C = A ∩ (B ∩ C)
A∩B =B∩A
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A∩∅=∅
A∩Ω=A
A ∩ B = Ā ∪ B̄
A∪A=A
(A ∪ B) ∪ C = A ∪ (B ∪ C)
A∪B =B∪A
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A∪∅=A
A∪Ω=Ω
A ∪ B = Ā ∩ B̄
Assoziativ
Kommutativ
Distributiv
Leere Menge
Grundmenge
de Morgan
Beispiel 1.3.
Die Distributivgesetze und die Regeln von de Morgan seien für folgenden
Fall erläutert:
Ω = { x ∈ N | x < 10 }, A = { 1, 2, 4 }, B = { 1, 2, 8, 9 }
und
C =
{ 1, 3, 5, 7 }.
ˆ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Hier sind B ∪ C = { 1, 2, 3, 5, 7, 8, 9 } und somit A ∩ (B ∪ C) = { 1, 2 }. Umgekehrt
sind A ∩ B = { 1, 2 } und A ∩ B = { 1 } und daher auch (A ∩ B) ∪ (A ∩ C) = { 1, 2 }.
ˆ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Hier sind B ∩ C = { 1 } und somit A ∪ (B ∩ C) = { 1, 2, 4 }. Umgekehrt sind
A ∪ B = { 1, 2, 4, 8, 9 } und A ∪ C = { 1, 2, 3, 4, 5, 7 } und daher auch (A ∪ B) ∩
(A ∪ C) = { 1, 2, 4 }.
ˆ A ∩ B = Ā ∪ B̄
Hier sind A ∩ B = { 1, 2 } und somit A ∩ B = { 3, 4, 5, 6, 7, 8, 9 }. Weiter sind Ā =
{ 3, 4, 5, 6, 7, 8, 9 } und B̄ = { 3, 4, 5, 6, 7 } und folglich Ā ∪ B̄ = { 3, 4, 5, 6, 7, 8, 9 }.
ˆ A ∪ B = Ā ∩ B̄
Hier sind A ∪ B = { 1, 2, 4, 8, 9 } und somit A ∪ B = { 3, 5, 6, 7 }. Weiter sind
Ā = { 3, 5, 6, 7, 8, 9 } und B̄ = { 3, 4, 5, 6, 7 } und folglich Ā ∩ B̄ = { 3, 5, 6, 7 }.
11
1 Mengen, Zahlen und Funktionen
1.9 Die Potenzmenge
In der Statistik geht man oft von einer meist
Ω
genannten Grundmenge aus und be-
trachtet die Elemente der Menge als Ausgänge etwa bei einem Fuÿballspiel 0 für ein
Unentschieden, 1 für einen Sieg der Heim- und 2 für einen Sieg der Auswärtsmannschaft. Die Grundmenge ist hier
beschreiben, etwa
{ 0, 1 },
Ω = { 0, 1, 2 }.
Die Teilmengen lassen sich ebenfalls
was für ein Unentschieden oder einen Sieg der Heimmann-
schaft steht. Die Teilmengen einer Menge sind so wichtig, dass man sie selbst zu einer
Menge zusammenfasst, der sogenannten Potenzmenge, einer Menge also, deren Elemente
Mengen sind. Ich halte das in einer Denition fest.
Denition 1.5.
Potenzmenge P(Ω) einer Menge Ω versteht man die Menge
Unter der
ihrer Teilmengen. Dabei ist zu beachten, dass die leere Menge
∅
und die Grundmenge
ebenfalls dazu zählen. Eine beliebige Teilmenge der Potenzmenge heiÿt
über
Ω
Mengensystem
Ω.
Ω = { 0, 1, 2 }. Zur Potenzmenge gehören alle
Teilmengen, also auch die leere Menge und Ω selbst. Weiter gibt es drei Teilmengen
mit nur einem Element, nämlich { 1 }, { 2 } und { 3 }, sowie drei Teilmengen mit je
zwei Elementen, und zwar { 0, 1 }, { 0, 2 } und { 1, 2 }. Die Potenzmenge P(Ω) und das
Mengensystem Z aller Mengen mit genau zwei Elementen sind somit
Betrachten wir als Beispiel die Menge
P(Ω) = { ∅, { 0 }, { 1 }, { 2 }, { 0, 1 }, { 0, 2 }, { 1, 2 }, { 0, 1, 2 } },
Z = { { 0, 1 }, { 0, 2 }, { 1, 2 } }
Beachten Sie bitte den Unterschied zwischen 2, dem Element von
welche eine Teilmenge von
Ω
2 ∈ Ω,
Die Potenzmenge von
Ω
und ein Element von
{ 2 } ⊂ Ω,
hat
P(Ω)
{ 2 } ∈ P(Ω),
8 = 2|Ω| = 23
Ω und der Menge { 2 },
ist, also
Z ⊂ P(Ω).
Elemente. Das ist kein Zufall, wie der
folgende Satz zeigt.
Satz 1. Es sei X eine endliche Menge mit n Elementen. Dann besteht die Potenzmenge
P(X) aus 2n Teilmengen. Die Anzahl der Elemente einer Menge wird Mächtigkeit genannt und mit |X| bezeichnet. Somit hängt für endliche Mengen die Mächtigkeit von X
und mit der von P(X) wie folgt zusammen:
|P(X)| = 2|X| .
(1.1)
n Elementen in der
X = { x1 , x2 , . . . , xn } schreiben. Bei jeder Teilmenge kann entschieden werden,
ob das Element xi dazu gehört oder nicht. Somit gehört zu jeder Teilmenge genau eine
Folge (z1 , z2 , . . . , zn ), wobei zi den Wert 1 hat, wenn xi zur Menge gehört und sonst den
n
Wert 0 annimmt. Es gibt aber genau 2 Folgen dieser Art.
Der Beweis sei angedeutet. Man kann jede endliche Menge mit
Form
Man kann die Teilmengen als Graph so anordnen, dass die leere Menge ganz unten
und die Grundmenge ganz oben steht und die restlichen Teilmengen dazwischen. Zwei
12
1.10 Kartesisches Produkt
Teilmengen werden durch einen Pfeil verbunden, wenn die tiefer stehende Menge selbst
Teilmenge der oberen Menge ist; man spricht von einem Hasse-Diagramm. Die folgende Abbildung ist auch aus dem deutschen Wikipedia und zeigt die Potenzmenge von
{ x, y, z }
als Hasse-Diagramm.
Abbildung 1.3: Die Potenzmenge von x, y, z als Hasse-Diagramm
1.10 Kartesisches Produkt
Denition 1.6.
Das Mengenprodukt
A × B := { (a, b) | a ∈ A, b ∈ B } .
ist die Menge aller geordneten Paare
Menge als
kartesisches Produkt
(a, b)
mit
a∈A
b ∈ B . Man
von A und B .
und
(nach René Descartes)
Beim kartesischen Produkt wird also jedes Element von
Geschrieben wird es als
A × B,
bezeichnet diese
A mit jedem von B kombiniert.
gelesen als A kreuz B.
Beispiel 1.4. Wir bilden das Mengenprodukt C = A×B von den Mengen A = { a, b, c }
und
B = { 1, 2 }.
Da jedes Element von
A
mit jedem von
B
verbunden wird, ergibt sich
C = A × B = { (a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2) }.
Beim kartesischen Produkt kommt es auf die Reihenfolge an, das Produkt
D = B×A
ist die folgende Menge
D = B × A = { (1, a), (1, b), (1, c), (2, a), (2, b), (2, c) }.
Bei den Elementen von
A×B
wie etwa
(a, 1)
steht an erster Stelle ein Element von
A
B . Bei den Elementen von B × A wie etwa (1, a) steht
erster Stelle ein Element von B gefolgt von einem Element von A. Die Reihenfolge
wesentlich, da die Paare geordnet sind und somit (a, 1) 6= (1, a) gilt.
gefolgt von einem Element von
an
ist
13
1 Mengen, Zahlen und Funktionen
Man kann das kartesische Produkt auch von zwei identischen Mengen bilden. Mit den
Bezeichnungen vom vorigen Beispiel ergeben sich
E = A × A = { (a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c) },
F = B × B = { (1, 1), (1, 2), (2, 1), (2, 2) }.
Statt
A×A
schreibt man meistens
A2 .
Das kartesische Produkt lässt sich auch von mehr als zwei Mengen bilden.
Denition 1.7.
n
Y
Das Mengenprodukt
Ai = A1 × A1 · · · × An := { (a1 , a2 , . . . , an ) | ai ∈ Ai , i = 1, . . . , n}
i=1
(a1 , a2 , . . . , an )
ist die Menge aller geordneten n-Tupeln
mit
ai
aus
Ai .
Ai leer, dann ist auch das kartesische Produkt
A, schreibt man auch hier vereinfacht An , d.h.
Ist eine der Mengen
Sind alle
Ai
gleich
n
A :=
n
Y
die leere Menge.
A.
i=1
Nun wird untersucht, wie viele Elemente die Produktmenge hat. Dabei bestehe das
|A1 |, |A1 |, . . . , |An |. Die ersA besetzt, und dafür gibt es
|A1 | Möglichkeiten. An der zweiten Stelle stehen die Elemente von A2 , wofür es |A2 |
Möglichkeiten gibt, in der Kombination ergeben sich |A2 | · |A2 | Möglichkeiten. Da man
Produkt nur aus endliche Mengen mit den Mächtigkeiten
te Position des n-Tupels wird von den Elementen von
diese Überlegung fortführen kann, folgt für die Mächtigkeit des kartesischen Produkts
die folgende Aussage:
Sind
A1 , A2 , . . . , An
endlich viele endliche Mengen. Dann ist auch ihr kartesisches
Produkt eine endliche Menge, und die Anzahl seiner Elemente ist gleich dem Produkt
der Mächtigkeiten der
Ai
|
n
Y
Ai | =
i=1
Wenn alle Mengen gleich
A
n
Y
|Ai |.
i=1
sind, gilt:
|An | =
n
Y
|A| = |A|n .
i=1
Dieses Ergebnis rechtfertigt die Bezeichnung Produktmenge.
A und B wie im Beispiel 1.4 die Mengen { a, b, c }
|A × A| = 9, |A × B| = |B × A| = 6 und |B × B = 4|.
Seien mit
so gilt
14
und
{ 1, 2 }
bezeichnet,
1.11 Relationen und Funktionen
Abbildung 1.4: Das kartesische Koordinatensystem
Kartesisches Koordinatensystem
2
y-Achse (Ordinate)
I. Quadrant
II. Quadrant
1
x-Achse (Abszisse)
0
-3
-2
-1
0
1
2
3
-1
III. Quadrant
IV. Quadrant
-2
1.10.1 Das kartesische Koordinatensystem
Auf René Descartes (1596 - 1650) selbst geht das kartesische Produkt
zurück, wobei
R2 = R × R
die Menge der reellen Zahlen bezeichnet, die man sich auf der Zahlen2
gerade vorstellen kann. Das kartesische Produkt R veranschaulicht man sich als eine
R
Ebene mit einem rechtwinkligen (kartesischen) Koordinatensystem. Die waagrechte Achse wird meist als
oder
Ordinate .
x-Achse
oder
Abszisse
y-Achse
Ursprung des
bezeichnet, die senkrechte Achse heiÿt
Die Achsen schneiden sich in einem Punkt, den man als
Koordinatensystems bezeichnet. Die Bezeichnungen x- und y-Achse sind zwar weit verbreitet, aber man darf natürlich auch andere Symbole verwenden. Die geordneten Paare
(a, b), a, b ∈ R
lassen sich dann als die Koordinaten eines Punktes in der Ebene deuten,
wobei der Ursprung die Koordinaten
denn der Wert von
(0, 0)
hat. Dabei ist die Reihenfolge wesentlich,
a wird waagrecht und der Wert von b wird senkrecht abgetragen. Die
Koordinatenachsen teilen die Ebene in vier Quadranten ein. Die Nummerierung erfolgt
im Gegenzeigersinn. In der Abbildung 1.4 sehen Sie ein kartesisches Koordinatensystem mit den üblichen Bezeichnungen und den Punkten
(−2, −1),
(2, 1), (−2, 1), (−2, −1)
sowie
die in den vier Quadranten liegen.
1.11 Relationen und Funktionen
Sehr häug stehen bestimmte Elemente
Für zwei Zahlen
x
und
nennt man Beziehungen
oder
⊂
x und
y
x∈A
in einer Beziehung zu Elementen
kann etwa die Beziehung
x>y
y ∈ B.
bestehen. In der Mathematik
Relationen und führt für wichtige Relationen Operatoren wie >
ein. Wenn bestimmte Elemente in einer Beziehung zueinander stehen, sagt man
y erfüllen die Relation R
oder stehen in der Relation R und schreibt xRy . Die
15
1 Mengen, Zahlen und Funktionen
Paare
(x, y),
die eine Relation erfüllen, bilden eine Teilmenge des kartesischen Produkts
A×B ihrer Mengen A und B . Die Menge aller Paare (x, y) mit x > y bildet beispielsweise
2
die Menge aller Punkte im R , die unterhalb der Winkelhalbierenden liegen. Der Begri
der Relation wird also auf den Mengenbegri zurückgeführt, wie die folgende Denition
zeigt.
Denition 1.8.
Seien mit
A
A und B zwei Mengen. Dann heiÿt jede Teilmenge R des karteA × B eine Relation . Für (x, y) ∈ R schreibt man manchmal xRy .
Seien
sischen Produkts
und
B
wieder die Mengen
{ a, b, c }
und
{ 1, 2 }
bezeichnet. Zur Veran-
schaulichung wird das kartesische Produkt durch ein Rechteck angedeutet, wobei die
A
Elemente von
auf der Abszisse und die Elemente von
B
auf der Ordinate abgetragen
werden. In der Abbildung 1.5 sehen Sie das kartesische Produkt und fünf Relationen.
Die Relation
R = { (a, 1), (a, 2), (b, 1), (b, 2), (c, 1) } hat fünf Elemente und ist im zweiten
Teilbild der Abbildung zu sehen.
Relationen lassen sich leicht auf den Fall erweitern, dass mehr als zwei AusgangsmenQn
gen vorliegen. Eine Relation ist eine Teilmenge des kartesischen Produkts
i=1 Ai der
Grundmengen
Ai .
Zeile ein n-Tupel
Solche Relationen werden durch Tabellen dargestellt, wobei in jeder
(a1 , a2 , . . . , an )
mt
ai ∈ Ai
steht. Die meisten Datenbanken bestehen
solchen Tabellen und werden daher relationale Datenbanken genannt. In der Abbildung
1.5 sind auch die Tabellen der fünf Relationen zu sehen.
Kartesisches Produkt
Relation R
Relation S
2
2
2
1
1
1
a
b
c
a
Relation T
b
c
a
Funktion f
2
2
1
1
1
b
c
a
b
c
c
Funktion g
2
a
b
a
b
A
a
a
b
b
c
R
B
1
2
1
2
1
f
A B
a 1
b 1
c 1
A
a
b
b
S
B
1
1
2
T
A B
a 1
c 1
g
A B
a 1
b 2
c 1
c
Abbildung 1.5: Kartesisches Produkt, Relationen und Funktionen
Wie Sie sehen, werden an Relationen nur geringe Anforderungen gestellt. Manche
Elemente von
A
oder
B
stehen mit mehreren Elementen der anderen Menge in einer
Beziehung, andere halten sich ganz zurück. Eine bestimmte besonders wichtige Klasse
von Relationen erfüllt aber weitere Bedingungen, die sogenannten Funktionen.
16
1.12 Funktionen
1.12 Funktionen
Bestimmte Relationen sind besonders wichtig und werden als Funktion bezeichnet. Bei
einer Funktion muss jedes Element von
A
mit genau einem Element von
Beziehung stehen, wobei aber zwei verschiedene Elemente
b∈B
zum gleichen Element
a1
und
a2
von
B in einer
A durchaus
in Beziehung stehen dürfen. Bei Funktionen spricht man
auch nicht mehr von Beziehung oder Relation, sondern man sagt, dass dem Element
a∈A
b∈B
das Element
Denition 1.9.
jedem Element
Seien
x∈D
zugeordnet wird. Das führt zu folgender Denition.
D
und
W
zwei Mengen. Eine
Funktion
ist eine Vorschrift, die
y ∈ W zuordnet. Diese Zuordnung wird durch
y = f (x) (lies: f von x) symbolisch ausgedrückt.
y = f (x) ist, verwendet man folgende Bezeichnungen
genau ein Element
ein Funktionszeichen wie
f
in der Form
Unter der Voraussetzung, dass
ˆ x
: unabhängige Veränderliche (Variable) oder Argument bzw. Urbild von
ˆ y
: abhängige Veränderliche (Variable) oder Funktionswert oder Bild von
ˆ D
ˆ W
:
:
Denitionsbereich
Wertebereich
x
der Funktion
der Funktion
ˆ G : { (x, f (x)) | x ∈ D }
nennt man den
Oft kann man die Vorschrift
f : D → W, x 7→ f (x).
y
f (x)
Graph
der Funktion
durch eine Formel angeben. Man schreibt dann
Beachten Sie den kleinen senkrechten Strich am zweiten Pfeil.
Am bekanntesten sind natürlich Funktionen einer reellen Veränderlichen. Dabei sind
Denitionsbereich
D
W Teilmengen von R und für die Zuordnung
2
etwa y = 2x − x + 1. Man schreibt dafür f : R →
und Wertebereich
gibt es eine Funktionsgleichung, wie
R, x 7→ f (x) = x3 + x2 − 9(x + 1). Manchmal schreibt man Funktionen in zwei Zeilen in
der folgenden Form
f: R→R
x 7→ f (x) = x3 + x2 − 9(x + 1).
In der ersten Zeile stehen also Denitions- und Wertebereich, in der zweiten Zeile die
Funktionsformel. Der Graph dieser Funktion ist in der Abbildung 1.6 zu sehen. Bei
f : D → W ist das Bild bzw. die Bildmenge oder der Bildbereich einer
Teilmenge M ⊆ D des Denitionsbereichs die Menge der Werte aus dem Wertebereich
W , die f auf M tatsächlich annimmt, d.h.
einer Funktion
f (M ) := { f (x) | x ∈ M }.
Das Bild
von
f
f (D)
des ganzen Denitionsbereichs
genannt und mit
Bild(f )
D
wird das
(1.2)
Bild
oder der
Bildbereich
bezeichnet. Manchmal werden aber die Bezeichnungen
Wertebereich und Bildbereich genau umgekehrt benutzt. Da der Bildbereich nicht immer
17
1 Mengen, Zahlen und Funktionen
y
20
y = x^3 + x^2 - 9x - 9
15
10
5
0
-4
-3
-2
-1
x
0
1
2
3
4
-5
-10
-15
-20
Abbildung 1.6: Graph einer reellen Funktion
leicht zu bestimmen ist, gibt man für den Wertebereich
Sicherheit das Bild
f (D)
W
eine Menge an, die mit
umfasst.
In vielen Problemen möchte man zu bestimmten Teilmengen des Wertebereichs
die Menge der Elemente bestimmen, die in
Diese Menge wird das
Urbild
von
B
f
eingesetzt, ein Element aus
−1
genannt und mit dem Symbol
Diese Menge ist immer eine Teilmenge des Denitionsbereichs
D
f
(B)
B
B
ergeben.
bezeichnet.
und lässt sich wie folgt
beschreiben
f −1 (B) := { x ∈ D | f (x) ∈ B }.
(1.3)
Dadurch wird eine Funktion deniert, die jeder Teilmenge des Wertebereichs eine Teilmenge des Denitionsbereichs zuordnet.
f und g der Abbildung 1.5. Beide sind
{ a, b, c } → { 1, 2 }. Der Bildbereich f (A) ist die Menge { 1 }, der Bild−1
bereich g(A) ist die Menge { 1, 2 }. Die Urbilder der Menge B = { 2 } sind f
(B) = ∅
−1
−1
und g
(B) = { b }. Die Urbilder der Menge C = { 1 } sind f (C) = { a, b, c } und
g −1 (C) = { a, c }.
3
2
Betrachten wir jetzt die Funktion f (x) = x + x − 9(x + 1) der Abbildung 1.6 und
bestimmen zunächst das Bild des Intervalls [−1, 0], also aller reellen Zahlen zwischen -1
und 0. Am Graphen kann man ablesen, dass das Bild das Intervall [−9, 0] ist. Das Urbild der Menge aller nichtnegativen reellen Zahlen setzt sich aus dem Bereich x ≥ 3 und
dem Intervall [−3, −1] zusammen. Bilder und Urbilder sind i.a. schwierig zu bestimmen.
Die Bestimmung des Bilds des Intervalls [−3, −1] erfordert die Berechnung des MaxiUntersuchen wir zunächst die Funktionen
Funktionen von
malwerts, wofür man Methoden der Dierentialrechnung benötigt. Falls Sie das schon
können, sollten Sie als Bild von
[−3, −1]
das Intervall
[0, 5, 049042476]
erhalten.
Eine besonders wichtige Funktion ist die sogenannte identische Funktion oder Identität
idD , die jedes Element des Denitionsbereichs D auf sich selbst abbildet, also idD (x) = x.
Oft schreibt man vereinfacht nur id.
Zu jeder Teilmenge A ⊆ D kann man eine reelle Funktion IA : D → R bilden, die
genau dann den Wert 1 annimmt, wenn x ∈ A liegt und sonst den Wert 0 annimmt.
18
1.13 Spezielle Eigenschaften mancher Funktionen
Diese Funktion hebt also die Elemente von
A
durch den Wert 1 hervor und wird als
In-
dikatorfunktion der Menge A bezeichnet. Für die Indikatorfunktion IĀ des Komplements
von
A
gilt
IĀ = 1 − IA .
Beispiel 1.5.
Seien
D = { u, v, w, y }
und
A = { uy }
sowie
Ā = { v, w }.
Es gelten
idD (u) = u, idD (v) = v, idD (w) = w, idD (y) = y.
IA (u) = 1, IA (v) = 0, IA (w) = 0, IA (y) = 1.
IĀ (u) = 0, IĀ (v) = 1, IĀ (w) = 1, IĀ (y) = 0.
1.12.1
Hintereinanderausführung von Funktionen
Man kann unter bestimmten Umständen zwei Funktionen
f
und
g
verknüpfen, in dem
f (x) in die Funktion g eingesetzt wird. Das ist aber nur möglich, wenn der
Wertebereich von f eine Teilmenge des Denitionsbereichs von g ist. Sei beispielsweise
√
√
die Funktion x 7→ ln( x − 1 + 2) betrachtet. Hier wird die Funktion f : x 7→
x − 1+1
in die Funktion g : y 7→ ln(y) eingesetzt. Der gröÿtmögliche Denitionsbereich von f
ist das Intervall Df = [1, ∞) mit dem Bild Bild(f ) = [2, ∞). Der Wertebereich der
Funktion g = ln(y) ist die Menge der positiven Zahlen Dg = (0, ∞), also gilt
der Wert von
Wf ⊆ Dg .
Immer wenn diese Grundbedingung gilt, kann die Funktion
g : Dg → Wg
(1.4)
f : Df → Wf
in die Funktion
eingesetzt werden. Es ergibt sich eine zusammengesetzte Funktion
h : Df → W g
x 7→ h(x) = g(f (x)).
Man nennt die so denierte Funktion
h
die
Hintereinanderausführung
(1.5)
(1.6)
oder Kompostion
g und f und verwendet das Symbol ◦, schreibt also h = g ◦ f . Die
h = g ◦ f erfolgt von rechts nach links: Zunächst wird f (x) bestimmt
Wert in g eingesetzt.
der Funktionen
Ausführung von
und dieser
1.13 Spezielle Eigenschaften mancher Funktionen
Bei allgemeinen Funktionen muss nicht jedes Element des Wertebereichs ein Urbild haben, aber manche Elemente des Wertebereichs können mehrere Urbilder haben. Die
Funktion
f
der Abbildung 1.5 nimmt den Wert 2 nicht an, aber der Wert 1 hat drei
Urbilder. Bei der Funktion
g
dagegen hat jedes Element des Wertebereichs mindestens
ein Urbild. Solche Funktionen heiÿen
bei
g
surjektiv . Die Urbilder sind aber weder bei f
noch
eindeutig. Es gibt aber Funktionen, wo jedes Element des Wertebereichs höchstens
ein Urbild hat, oder anders gesagt, wo jedem Element des Wertebereichs ein eigenen
Wert zugewiesen wird, der sonst nicht mehr angenommen wird. Eine Funktion mit dieser Eigenschaft heiÿt
injektiv . Die stärkste Forderung erfüllen bijektive
Funktionen, die
19
1 Mengen, Zahlen und Funktionen
sowohl injektiv als auch bijektiv sind. Die genaue Denition der drei Eigenschaften sieht
so aus.
Denition 1.10.
Eine Funktion
ˆ
surjektiv, wenn für alle y
ˆ
injektiv,
wenn zu jedem
Jedes Element aus
ˆ
bijektiv, wenn f
W
f
aus
y
von
W
aus
heiÿt
mindestens ein
W
höchstens ein
x
aus
x
D
aus
mit
D
y = f (x)
x
aus
D
mit
Sind sowohl der Denitionsbereich
f: D →W
dann kann eine Funktion
existiert.
y = f (x).
existiert mit
hat also genau ein oder kein Urbild.
sowohl injektiv als auch surjektiv ist. Jedes Element
also genau ein Urbild
ˆ
D→W
D
y
aus
W
hat
y = f (x).
als auch der Bildbereich
W
endliche Mengen,
nur dann
höchstens so viele Elemente wie
D
hat, es gilt also
|D| ≤
W
mindestens so viele Elemente wie
D
hat, es gilt also
|D| ≥
W
genauso viele Elemente wie
surjektiv sein, wenn
W
|W |.
ˆ
injektiv sein, wenn
|W |.
ˆ
bijektiv sein, wenn
D
hat, es gilt also
|D| = |W |.
Bitte beachten Sie, dass es sich dabei um notwendige nicht um hinreichende Bedingungen
handelt.
Quälen wir ein weiteres Mal die Funktionen
f
f
und
g
der Abbildung 1.5. Die Funktion
g surjektiv, aber nicht injektiv
ist. Da die Mächtigkeiten der Denitionsmenge A = { a, b, c } und des Wertebereichs
B = { 1, 2 } die Werte 3 und 2 haben, kann es keine injektive Funktion von A → B geben,
ist weder injektiv noch surjektiv, während die Funktion
wohl aber surjektive Funktionen. Umgekehrt kann es keine surjektiven Funktionen von
B → A
geben, wohl aber injektive, etwa die Funktion
h
mit
h(1) = a
und
h(2) = b.
Diese Funktion ist aber nicht bijektiv, da c kein Urbild hat.
3
2
Die Funktion f : R → R, f (x) = x + x − 9(x + 1) der Abbildung 1.6 ist surjektiv, da
jeder Wert mindestens einmal angenommen wird, aber nicht injektiv, da z.B. der Wert
0 drei Urbilder hat.
g : R → R, x 7→ y = mx + b ist für m 6= 0 bijektiv, da jeder
y ∈ R genau einmal angenommen wird, das Urbild von y ist x = (y − b)/m. Da
−1
jedem y ein eindeutiger Wert x zugeordnet wird, ergibt sich eine Funktion g
:R →
R, x 7→ y = (x − b)/m. Diese Funktion nennt man die Umkehrfunktion von g . Allgemein
Jede lineare Funktion
Wert
deniert die Umkehrfunktion für bijektive Funktionen wie folgt.
Denition 1.11. Sei f eine bijektive Funktion von D → W . Die Umkehrfunktion oder
inverse Funktion oder kurz die Inverse ist die Funktion, die jedem Element y ∈ W sein
eindeutig bestimmtes Urbildelement x ∈ D zuweist. Die Umkehrfunktion wird mit dem
−1
Symbol f
bezeichnet und hat W als Denitionsbereich und D als Wertebereich.
20
1.13 Spezielle Eigenschaften mancher Funktionen
Eine Funktion, deren Umkehrfunktion existiert, wird auch als invertierbar bezeichnet.
−1
Für invertierbare Funktionen gelten die Formeln f
(f (x)) = x und f (f −1 (y)) = y für
−1
alle x ∈ D bzw. für alle y ∈ W . Natürlich ist f wieder die Umkehrfunktion von f
.
Das hochgestellte
machung von
f.
Beispiel 1.6.
−1
ist also nicht als Potenz zu deuten, sondern als die Rückgängig-
Betrachten wir zum Abschluss noch ein weiteres Beispiel.
Seien zunächst die Mengen
D = { 1, 2, 3, 4 }
und
W = { 6, 7, 8, 9 } beD × W , die keine
trachtet. In der Abbildung 1.7 sehen Sie ganz links eine Relation auf
Funktion ist, denn der Wert 1 hat zwei Zuordnungen, der Wert 4 dagegen keine, also
gleich zwei Verletzungen der Anforderungen an eine Funktion. Im mittleren Bild ist der
x ∈ D ist genau ein y ∈ W
−1
zugeordnet. Im nächsten Bild sehen Sie dann den Graph der Umkehrfunktion f
. Ganz
Graph einer bijektiven Funktion
f: D →W
zu sehen. Jedem
rechts folgen dann die Wertetabellen der beiden Funktionen.
Funktion f
Keine Funktion
9
9
4
8
8
3
7
7
2
1
2
3
4
f-1
y x
6 2
7 1
8 4
9 3
1
6
6
f
x y
1 7
2 6
3 9
4 8
Inverse f^-1
1
2
3
6
4
7
8
9
Abbildung 1.7: Bijektive Funktion und Inverse
Eine injektive Abbildung von
M
nach
P(M )
ist
f (x) := { x }.
21
Index
Abszisse, 15
Allquantor, 3
Aussage, 2
Aussageform, 2
Betrag, 4
Bild, 17
Bildbereich, 17
Bildmenge, 17
Dezimalbruch, 6
Dezimalbruchentwicklung, 6
Elemente, 1
Existenzquantor, 3
Funktion
bijektive, 19
Denition, 17
irrationale Zahlen, 3
kartesisches Produkt, 13
Menge, 1
Aufzählung, 1
Beschreibung, 1
Mengensystem, 12
Obermenge, 8
Ordinate, 15
Potenzmenge, 12
Primzahl, 6
Quantor, 3
Relation, 16
Relationen, 15
Denitionsbereich, 17
Teiler, 6
injektive, 19
teilerfremd, 6
inverse, 20
Teilmenge, 8
surjektive, 19
echte, 8
Wertebereich, 17
Umkehrfunktion, 20
Gegenzahlen, 4
Urbild, 18
Graph, 17
Ursprung, 15
Hintereinanderausführung, 19
x-Achse, 15
Indikatorfunktion, 19
y-Achse, 15
Intervall
abgeschlossenes, 4
Zahlengerade, 3
links halboenes, 4
oenes, 4
rechts halboenes, 4
Inverse, 20
23