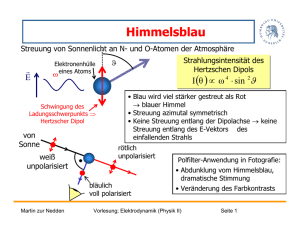
VL 11, 17.05.2011
Werbung

3. Magnetostatik • • • • 3.1. 3.2. 3.3. 3.4. Permanentmagnete Magnetfelder stationärer Ströme Kräfte bewegter Ladungen im Magnetfeld Materie im Magnetfeld Martin zur Nedden Vorlesung; Elektrodynamik (Physik II) Seite 1 3.1. Permanentmagnete Altertum: Fund magnetischer Steine bei Magnesia (Kleinasien) Heute: Magnetfelder ↔ Empirische Befunde: elektrische Ströme magnetische Materialien ↔ mikroskopische Kreisströme und Spins a) Es gibt zwei magnetische Pole: N ( Nord ) S ( Süd ) Anziehung Abstoßung b) Es wurden bisher keine magnetischen Monopole beobachtet ⇒ Sägen ⇔ Magnetfeldlinien sind stets geschlossen, d.h. sie enden nie Martin zur Nedden Vorlesung; Elektrodynamik (Physik II) Seite 2 Magnetisches Kraftgesetz sehr lange Magnetstäbe → quasi isolierte Magnetpole r F pp11 ,, pp22:: „Polstärken“ „Polstärken“ r r ... p1 Analogie zum Coulomb-Gesetz: 1 f= 4π µ 0 Definition: , ... p2 r p1 p 2 r F = f ⋅ 2 ⋅ er r −7 Vs µ 0 = 4 π ⋅ 10 Am Folge: Quantifizierung der Polstärke analog zur elektrischen Ladung Martin zur Nedden Vorlesung; Elektrodynamik (Physik II) Motivation später: 1 ε0 µ 0 = 2 c [p] = Vs [Q] = As Seite 3 Magnetisches Feld Feldkonzept (im Vakuum): p2 → 0 ist Probepol im Magnetfeld von p1 Definition: Magnetische Erregung r r r r F( r ) H (r ) = lim p 2 →0 p 2 [H ] = A m −1 Definition: Magnetische Feldstärke r r r r B( r ) = µ 0 ⋅ H( r ) [B] = Vsm−2 Einheiten der magnetischen Feldstärke: SI: 1T = 1Tesla = 1Vsm −2 Beispiele: cgs-System: 1G = 1Gauss = 10−4 T • Erdmagnetfeld (Oberfläche) ≈ 20 µT • NMR-Tomograph: ≈ 1 T • Supraleitende Magnete (Beschleuniger): ≈ 10 T • Neutronensterne (Oberfläche): ≈ 108 T Martin zur Nedden Vorlesung; Elektrodynamik (Physik II) Seite 4 3.2. Magnetfelder stationärer Ströme Beobachtung: I • Stationäre Ströme erzeugen Wirbelfelder • Feldrichtung wechselt mit Stromrichtung r • B ∝ r −1 , B ∝ I ⇒ B(r ) ⋅ (2π r ) = const. ⋅ I r B Quantitativ beschreibbar durch: Amperesches Gesetz r r ∫ Bds = µ0 I mit r r I = ∫ j dA A C Stokesscher Satz ⇒ r r rot B = µ 0 j nicht konservativ! Das Magnetfeld hat kein skalares Potential! Martin zur Nedden r j Vorlesung; Elektrodynamik (Physik II) Rundweg C Seite 5 Fläche A Magnetisches Potential Beobachtung: es gibt keine magnetischen Monopole ⇔ das Magnetfeld ist quellenfrei ⇔ magnetische Feldlinien sind geschlossen ⇔ r div B = 0 r r • wegen div B = 0 existiert ein Vektorpotential A mit r r • A ist nicht eindeutig ⇒ Eichbedingung div A = 0 Zusammenfassung: Martin zur Nedden r r rot B = µ 0 j r div B = 0 Vorlesung; Elektrodynamik (Physik II) r r B = rot A r r rot A = B r div A = 0 Seite 6 Stromdurchflossener Leiter r r Symmetrie ⇒ B( r ) = B(r ) ⋅ eϕ r r r r ∫ B(r )d s = 2π r ⋅ B(r ) I0 r0 1 , r ≥ r0 µ 0 I = µ 0 I0 ⋅ 2 (r r0 ) , r < r0 µ 0 I0 B(r ) = ⋅ 2π r Martin zur Nedden , r ≥ r0 1 r B B ∝r ∝1 r 2 r , r < r0 r0 Vorlesung; Elektrodynamik (Physik II) r0 Seite 7 r Zylinderspule r r B=0 außen innen Streufeld: I0 r r B = B0 = const. r r r ∫ B(r )d s = B0 L µ 0 I = µ 0 N I0 mit N n= L Wicklungsdichte Martin zur Nedden I0 I0 L, N Windungen ⇒ B0 = µ0 nI0 r r B≠0 r B real: endlich lang, endliche Wicklungsdichte Streufelder entweichen im Unendlichen … r r B=0 r B = const. … ideal: unendlich lang und dicht gewickelt Vorlesung; Elektrodynamik (Physik II) Seite 8 Helmholtzspule Praktische Realisierung des (fast) homogenen B-Feldes: B(z) (auf Achse) R R z Helmholtz-Spule Martin zur Nedden z Optimale Homogenität im Spulenzentrum Vorlesung; Elektrodynamik (Physik II) Seite 9