Himmelsblau

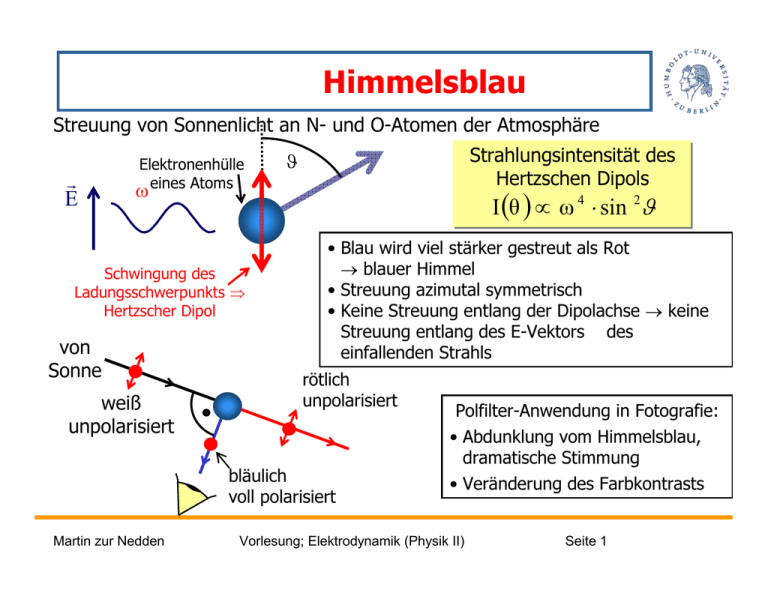
Himmelsblau
Streuung von Sonnenlicht an N- und O-Atomen der Atmosphäre
r
E
Elektronenhülle
eines Atoms
Strahlungsintensität des
Hertzschen Dipols
ϑ
ω
Schwingung des
Ladungsschwerpunkts ⇒
Hertzscher Dipol
von
Sonne
weiß
unpolarisiert
I (θ ) ∝ ω 4 ⋅ sin 2ϑ
• Blau wird viel stärker gestreut als Rot
→ blauer Himmel
• Streuung azimutal symmetrisch
• Keine Streuung entlang der Dipolachse → keine
Streuung entlang des E-Vektors des
einfallenden Strahls
rötlich
unpolarisiert
bläulich
voll polarisiert
Martin zur Nedden
Polfilter-Anwendung in Fotografie:
• Abdunklung vom Himmelsblau,
dramatische Stimmung
• Veränderung des Farbkontrasts
Vorlesung; Elektrodynamik (Physik II)
Seite 1
Polarisation
Maxwell-Gleichungen ⇒ elektromagnetische Wellen (z.B. Licht)
Spezialfall: ebene monochromatische elektromagnetische Welle
rr
r r
E = E 0 ⋅ ei (k r −ω t )
rr
r r
B = B0 ⋅ ei (k r −ω t )
r r
|3
E 0 , B0 ∈ C
r r
r
r
k ⊥ B0 ⊥ E 0 ⊥ k
r r
r
r
k ⊥ B0 ⊥ D 0 ⊥ k
physikalisch relevant:
Ausbreitungsrichtung:
Dispersionsrelation:
Martin zur Nedden
im neutralen Medium
r
r
Re E , Re B
r r r
S ∝ E 0 × B0
r
ω = c⋅ k
im Vakuum
(Vakuum)
Vorlesung; Elektrodynamik (Physik II)
r r
S || k
Vakuum:
c r
ω= ⋅ k
n
Seite 2
(Medium)
Polarisation
rr
r r
i (k r − ω t )
E = E0 ⋅ e
rr
r r
B = B0 ⋅ ei (k r −ω t )
Definition:
Die Auszeichnung einer Schwingungsebene des E-Feldes
Polarisation
Beispiel:
heißt
r
E
Hertzscher Dipol
schwingende
Ladung
Glühbirne ⇒
Martin zur Nedden
Polarisation || Dipolachse
statistisch verteilte Hertzsche Dipole
unpolarisiertes Licht
Vorlesung; Elektrodynamik (Physik II)
r
E
Seite 3
Lineare Polarisation
ϕ=0 ⇒
2
2
a
+
b
= 1 r  cos α 
r a
r
r
p= 
⇒
p=
 = cos α ⋅ e x + sin α ⋅ e y
 b
 sin α 
y
Horizontale Polarisierung
r
p
r r
α = 0 ⇒ p || e x
α
Vertikale Polarisierung
α=
π
2
r r
⇒ p || e y
r
E
x
Zeitlich und räumlich
feste Schwingungsebene
Martin zur Nedden
Vorlesung; Elektrodynamik (Physik II)
Seite 4
Zirkulare Polarisation
ϕ =±
π
1
, a =b=
2
2
⇒
r
1  1 
1  1  r
π
p R, L =
=
±
i
e 2 
 ± i  = e R, L
2 
2  

Nach Photon-Spin (Quantenmechanik)... (optische Nomenklatur genau umgekehrt )
ϕ = + π2 ⇔ rechts-zirkular polarisiert
ϕ = − π2 ⇔
Interpretation:
Re E x =
E0
=
E0
Re E y =
E0
cos (k z − ω t + ϕ x )
2
cos (ω t − k z − ϕ x )
2
= ±
2
y
cos (k z − ω t + ϕ x ±
E0
2
zz == const.
const.
ϕ =+
π
2
r
Re E
)
ωt + const.
sin (ω t − k z − ϕ x )
Drehende
Drehende Rechts-/Linksspirale
Rechts-/Linksspirale
entlang
entlang z-Achse
z-Achse
Martin zur Nedden
π
2
links-zirkular polarisiert
x
t = const.
umgekehrte Drehbewegung
Vorlesung; Elektrodynamik (Physik II)
Seite 5
→
Charakterisierung:
• Frequenz
• Wellenlänge
• Photonenergie
Elektromagnetisches
Frequenzspektrum
ν =
ω
2π
λ = cν
E = hν
[Hz ]
[m ]
= h ω [eV ]
Plancksches Wirkungsquantum
h = 6.626⋅⋅10−34 Js
h = 2hπ
(Photon: Feldquant des e.m.-Feldes)
Ultralangwelle:
Ultralangwelle:
νν == 11 Hz
Hz
λλ == 300000
300000 km
km
400 nm … 700 nm
Violett … Rot
kosmische
kosmische Gammastrahlung:
Gammastrahlung:
14 eV
EEγγ ≲≲ 10
1014
eV == 100
100 TeV
TeV
−20
λλ ≳≳ 10
m
10−20 m
Martin zur Nedden
Vorlesung; Elektrodynamik (Physik II)
Seite 6