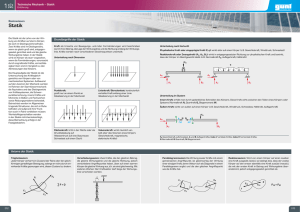
Kräfte ( ) ( )
Werbung

Kräfte Das Gravitationsgesetz FG G m1 m2 r2 Gewichtskraft FG m g Symbol Einheit FG Gravitationskraft N m1, m2 Masse kg FG m g Gewichtskraft N Fallbeschleunigung m/s2 G r Federkraft (Federgesetz nach Hooke) F D s Grösse F D s Gravitationskonstante Naturkonstante Abstand zwischen den Massenmittelpunkten Masse N m2 kg 2 m kg Federkraft N Federverlängerung m Federkonstante Zwischen zwei Körpern wirkt eine Anziehungskraft, die Gravitationskraft. G 6.67 1011 N m2 kg 2 mErde 5.974 1024 kg Erdradius rErde 6.378 106 m Die Gewichtskraft auf der Erdefolgt aus dem Gravitationsgesetzt: Erdmasse und Erdradius einsetzen. g=9.81 m/s2 N/m Normalkraft FN Die Normalkraft FN ist die Kraft von der Unterlage auf einen Körper. Sie wirkt immer senkrecht zur Unterlage. Reibungskraft FR R FN Luftwiderstand FLW 1 cW A v 2 2 Schiefe Ebene FR Reibungskraft N FN Normalkraft N R Luftwiderstandskraft N cW Luftwiderstandbeiwert - A v FG FN FG cos FN FR R FN - FLW F G FGx , FGy FGx FG sin Reibungszahl FGx FR Dichte von Luft Windangriffsfläche Geschwindigkeit kg/m3 m2 m/s Gewichtskraft, in Komponenten zerlegt N Normalkraft N x-Komponente, «Hangabtriebskraft» Reibungskraft, Roll-bzw. Gleitreibung wirken entgegen der Bewegungsrichtung. Seite 9 Es gibt drei Arten von Reibung: Gleitreibung, Haft- und Rollreibung. Sie werden nach derselben Formel berechnet. bei 20°C ca. 1.22 kg/m3 Je kleiner der Wert umso kleiner die Luftwiderstandskraft (Windschlüpfiger) rechtwinklig zur Windgeschwindigkeit N N FGx > FReibung und FReibung nach oben: Der Körper gleitet nach unten Dynamik Grundgesetz der Dynamik Zweites newtonsches Gesetz Fi m a Symbol F i m a i Grösse i Einheit Vektorsumme aller Kräfte i entspricht der Gesamtkraft N Beschleunigung m/s2 Masse kg Bewegungsgesetz: Die Gesamtkraft, welche auf einen Körper wirkt, ist das Produkt aus Masse und Beschleunigung. Trägheitsgesetz Erstes newtonsches Gesetz Wenn keine Gesamtkraft auf einen Körper wirkt, so ändert sich seine Geschwindigkeit und Bewegungsrichtung nicht. Spezialfall des zweiten newtonschen Gesetztes: Fi m a 0 , keine Beschleunigung, v bleibt konstant. i Wechselwirkungsgesetz Drittes newtonsches Gesetz F2 2 F1 1 F2 2 F1 Aktionskraft 1 Reaktionskraft N N Körper eins wirkt auf Körper zwei Körper zwei wirkt auf Körper eins Aktions- und Reaktionskraft greifen an verschiedenen Körpern an. Bezugsystem Wir wählen für unsere Betrachtungen immer unbeschleunigte Bezugssysteme (Inertialsysteme). Darin können wir für jede Kraft eine Ursache benennen und es gilt das Bewegungsgesetz (zweites newtonsche Gesetz). Zweikörpersysteme F m m a i i Fi mi a F1 F2 1 2 F Summe der Kräfte N m1+m2 a Gesamtmasse kg Fi Fi Seilkraft 1 bzw. 2 N Betrag der Seilkraft N i i Beschleunigung Seite 10 m/s2 Die Umlenkrolle lenkt die Kraftrichtungen um. Darum ist die Summe der Kräfte die Differenz der Gewichtskräfte. Beide Massen werden mit gleichem Betrag beschleunigt. Nach dem Wechselwirkungsgesetz sind die Beträge der Seilkräfte gleich gross. Für die Berechnung der Seilkraft wird nur ein Körper betrachtet. Statik Gleichgewicht Im statischen Gleichgewicht kann sich ein Körper mit konstanter Geschwindigkeit geradlinig bewegen oder mit einer konstanten Drehzahl rotieren. Symbol Statik Grösse Einheit Bedingung 1, Summe aller Kräfte gleich Null F F i i 0 i x,i 0 und Fy ,i 0 i Drehmoment M F r F l sin Fi angreifende Kraft N F x, i Komponente x, bzw. y N M F r l Drehmoment Nm wirksame Hebellänge m Kraft am Hebelende Hebelarm (Länge) Winkel zwischen Hebel l und Kraft Mi Drehmoment inklusive Vorzeichen Die Vektorsumme aller Kräfte ist null. Dies gilt auch für die einzelnen Komponenten x, y (und z). N m Statik Bedingung 2, Momentengleichung M i i 0 Seite 11 Nm Vorzeichenkonvention positiv: gegen den Uhrzeigersinn negativ: im Uhrzeigersinn Statik: Kräfteplan Schwerpunkt Der Punkt eines Körpers, in dem die gesamte Masse vereinigt gedacht werden kann, heisst Schwerpunkt oder Massenmittelpunkt. Für die Berechnung der Gewichtskraft, des Drehmoments oder der potenziellen Energie kann jeder Körper als Massenpunkt im Schwerpunkt vereinfacht werden. Alle Kräfte greifen an einem Punkt an Die Wirkungslinie (gestrichelt) ist die Gerade, die durch die Richtung des Kraftvektors gegeben ist. Eine Kraft kann entlang ihrer Wirkungslinie verschoben werden, ohne dass sich die Wirkung der Kraft auf diesen Körper ändert. Berechnung der Kräfte mit dem Sinussatz und den Winkeln im Dreieck Mehrere Kräfte, verschiedene Angriffspunkte Wenn die Kräfte an unterschiedlichen Punkten angreifen, entstehen Drehmomente. 1: Die Drehachse dort festlegen, wo eine unbekannte Kraft wirkt, die unbekannte Kraft verursacht kein Drehmoment, (Hebel =0 m) 2: Mit der Bedingung 2 der Statik, Momentengleichung, beginnen. 3: Mit der Bedingung 1 der Statik, Kräftesumme = 0, die restliche Kraft bestimmen. Seite 12 Am Schwerpunkt (SP) eines Körpers greift die Gewichtskraft FG an. Der SP liegt auf einer Schwerelinie. Arbeit und Energieformen Mechanische Arbeit W F s W F cos( ) s Symbol W F s Grösse Arbeit Einheit J Kraft Wegstrecke N m 1J = 1Nm 1 kg m 2 s2 1kWh = 3.6 106 J Wärme und Arbeit Mechanische Arbeit kann in Wärme und Wärme kann in mechanische Arbeit umgewandelt werden. Die beiden physikalischen Grössen sind äquivalent zueinander. Unterscheidung zwischen Arbeit und Energie Mit der Arbeit wird ein Prozess (Vorgang) beschrieben. Beispiel Hubarbeit, Bremsarbeit, (Analogie: Geldverdienen) Ein System hat Energie, damit wird ein Zustand beschrieben. Beispiel Lageenergie, Bewegungsenergie, (Analogie: Kontostand) Potenzielle Energie E pot ,i m g hi Kinetische Energie Ekin ,i 1 m vi2 2 Elastische Energie Eelast ,i 1 2 D si 2 Brennstoff, Nutzenergie ENutz mBrennstoff Hu Epot,i potenzielle Energie, Zustand i J Es gibt kein absolutes Mass für die potenzielle Energie. Die Bezugshöhe h = 0 wird frei gewählt. Für Höhen unterhalb null ist hi 0 m g hi Masse kg Höhe, Zustand i m Ekin i kinetische Energie, Zustand i J Geschwindigkeit, Zustand i m/s Eelast i elastische Energie, Zustand i J si Federverlängerung, Zustand i m Differenz zum ungespannten Zustand Wärme Q oder mechanische Energie vi D Ortsfaktor Federkonstante N/kg N/m ENutz Nutzenergie J m Br . Hu Heizwert Masse Brennstoff kg Wirkungsgrad Beim Heizwert Hu ist die Kondensation von Wasserdampf nicht berücksichtigt beim Brennwert Ho jedoch schon. H o H u Seite 13 - MJ/kg von der Bezugshöhe abhängig Die kinetische Energie kann nie mit der Durchschnittsgeschwindigkeit oder einer Geschwindigkeitsdifferenz berechnet werden. Die Spannarbeit wird im F-sDiagramm als Fläche unter der Kurve berechnet. Üblicherweise in Prozent angegeben Energieerhaltung im abgeschlossenen System Abgeschlossene Systeme Ein abgeschlossenes System hat keine Wechselwirkung mit der Umwelt. In einem abgeschlossenen System bleibt die Gesamtenergie konstant Zustand 2 Zustand 1 Energieform potenzielle Energie E pot m g h1 kinetische Energie Ekin elastische Energie Eelast Zustand 1 Antriebs-, Treibstoff-Energie… EBrennstoff mBrennstoff H u Leistung Momentane Leistung Pmomentan F v Wirkungsgrad E Nutzen EAufwand Ekin 1 2 D s1 2 Summe 1 Summe E P t 1 m v12 2 P Symbol Grösse Einheit W J Energiedifferenz Zeitdauer s Pmom Momentane Leistung, bei der Geschwindigkeit v W F Kraft N Wirkungsgrad - E Aufwand eingesetzte Energie J v ENutzen Momentane Geschwindigkeit genutzte Energie Seite 14 E kin 0 1 2 D s2 2 Summe 2 E t Senkrechter Wurf: Im höchsten Punkt gilt W FFahrwiderstand s = Mittlere Leistung 1 m v22 2 Eelast oder Eelektrisch Zustand 2 entstandene Reibungswärme Mittlere Leistung E pot m g h2 m/s J 1W 1J/s 1J 1 W s 3.6 MJ 1kWh 1PS 735 W