plasma feldstärke

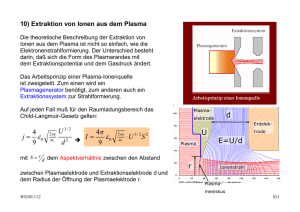
10) Extraktion von Ionen aus dem Plasma
Die theoretische Beschreibung der Extraktion von
Ionen aus dem Plasma ist nicht so einfach, wie die
Elektronenstrahlformierung. Der Unterschied besteht
darin, daß sich die Form des Plasmarandes mit
dem Extraktionspotential und dem Gasdruck ändert.
Das Arbeitsprinzip einer Plasma-Ionenquelle
ist zweigeteilt. Zum einen wird ein
Plasmagenerator benötigt, zum anderen auch ein
Extraktionssystem zur Strahlformierung.
Auf jeden Fall muß für den Raumladungsbereich das
Child-Langmuir-Gesetz gelten:
Plasma-
d
elektrode
Erdelek-
4
j = ε0
9
2 eq
mi
U
3/ 2
d
2
Î
4π
ε0
I=
9
2 eq
mi
⋅U
3/ 2
S
U
2
mit S = r d dem Aspektverhältnis zwischen den Abstand
zwischen Plasmaelektrode und Extraktionselektrode d und
dem Radius der Öffnung der Plasmaelektrode r.
Plasma
r
trode
E=U/d
Ionenstrahl
Plasmameniskus
WS2011/12
10.1
Mit der elektrischen Feldstärke kann das Gesetz wie folgt
dargestellt werden:
I=
4π
ε0
9
2 eq
mi
S ⋅ r 3 / 2 E 3 / 2 = 1.71 *10− 7
q
S ⋅ r3/ 2E3/ 2
A
Beispiel: q/A =1, S=1, U = 10000 V --> I = 0.171 A
Damit ist keine Aussage über die Strahlqualität getroffen!
Die emittierende Oberfläche des Plasmas (Grenzschicht) wird auch Plasmameniskus genannt:
Wie unterscheiden sich die Bedingungen bei der Plasmaextraktion von der Elektronenemission:
• Pierce-Rand ist nur eine gute Näherung, wenn das Plasma das gleiche Potential wie die
Elektrode besitzen würde (Plasmapotential).
• Die Plasmaelektrode müsste am Rand infinitesimal dünn sein, was technisch nicht realisierbar ist.
• Ionenemission ist nicht homogen über den Querschnitt, wie bei Elektronen aus einer Kathode, da
das Plasma in der Nähe der Elektrode immer weniger dicht ist (Plasmarand).
Um den Anodenlinseneffekt zu kompensieren muß der Plasmameniskus konkav sein.
WS2011/12
10.2
Plasmadichte zu hoch, bzw.
Feldstärke zu gering !
Plasmadichte bzw. Feldstärke sind optimal,
„Matched case“,
r und α sind an der Erdelektrode minimal!
Plasmadichte zu gering, bzw.
Feldstärke zu hoch !
Im Extraktionsraum ist der Ionenstrahl nicht mehr kompensiert, d.h. die Ladungsneutralität ist aufgehoben, da die Elektronen durch die Extraktionsspannung in das Plasma zurückgedrückt werden.
WS2011/12
10.3
Die Feldstärke im Extraktionsraum bestimmt
wie stark die Dichte der Plasmarandschicht
reduziert wird und wie weit das Extraktionspotential in das Plasma hineinreicht.
Die Dicke der Randschicht ergibt sich aus:
d sheath = λD ⋅
WS2011/12
e ⋅ φ Zug
kT
10.4
Plasmarand bei Extraktion von Ionen:
Ionen der Masse M mit schon gerichteter Geschwindigkeit durch das Extraktionsfeld E=Ui/d mit
2qU i
vion =
M .
Aus der Kontinuitätsgleichung folgt:
der Ionen im Plasma sind. Aus
1
2
Mvi ( z ) 2 = 12 Mv0 − qφ ( z )
n 0 v 0 = ni ( z ) v i ( z )
2
folgt
wobei n0 und v0 Dichte und Geschwindigkeit
⎛ 2qφ ( z ) ⎞
⎟
ni ( z ) = n0 ⎜⎜1 −
2 ⎟
Mv0 ⎠
⎝
−1 / 2
Mit − φ ( z ) = U p − U (Up = Plasmapotential) gilt dann für Ionen am Plasmarand:
ρi ( z) =
1−
ρi0
2qφ ( z )
Mv02
⎛U −U p ⎞
kTe
⎟⎟
ne = ne 0 exp⎜⎜
U
=
e
Für die Elektronen gilt die Boltzmannverteilung:
e
⎝ U e ⎠ mit
ene 0
eni 0
∂ 2U
−
=
2
z
∂
⎛U − U ⎞
U p −U
Damit wird die Poissongleichung zu
ε 0 exp⎜ p
⎟
Ue ⎠ ε 0 1 + U
⎝
i
WS2011/12
10.5
Lösung der Gleichung nur numerisch, jedoch Vereinfachung durch Normierung mit
η=
U p −U
Ue
U
z
, β = e ,ζ =
Ui
λD
und
λ2D
Ue
=
ε0
en0
( 1 + βη − 1) + 2 exp(− η ) − 2
∂ 2η
1
1
⇒ − 2 =
−
∂ζ
exp(η )
1 + βη
(i) oder
Numerisch lösbar oder analytisch für
η → 0 . Dann lassen sich die Funktionen entwickeln und es folgt
4
∂η
=
∂ζ
β
⎛
⎞
β
β
∂η
≈ 1 − ⋅η ⇒ η = η0 exp⎜⎜ (ζ − ζ 0 ) 1 − ⎟⎟
∂ζ
2
2⎠
⎝
Dies verlangt demnach β ≤ 2 oder U e ≤ 2U i . Dies ist das sogenannte Bohmsche Schichtkriterium.
Damit keine "Ionenverarmung" entsteht, werden in einem Teil des Grenzschichtbereiches (z>λD) die
Ionen bis auf Schallgeschwindigkeit beschleunigt. ß = 1 ist eine gute Annahme, wenn keine
Messdaten vorliegen. Innerhalb von 6.5* λD fällt das Potential von U p − 0.01 ⋅ U e auf U p − U e und
innerhalb von 20-50* λD fällt es auf Wandpotential ab.
WS2011/12
10.6
Vergleich mit Child-Langmuir:
∂ 2U
1
j
=
∂x 2 ε 0 2me U
η=
mit
U
U Anode
η ′′ =
(d = Anodenabstand) -->
, ζ =
3z
2d
1
η
(ii)
Der Vergleich von (i) und (ii) ist nebenstehen
dargestellt. Man erkennt, daß sich (i) und (ii)
(Child-Langmuir) für große
ζ
annähern.
Ist d >> λD oder die Extraktionsspannung hoch,
so wird die Plasmaextraktion der Elektronenemission ähnlich.
WS2011/12
10.7
Wie muß nun die Plasmaelektrode aussehen?
Piercerand?
Die Kontur der Plasma-Elektrode müsste in
unmittelbarer Nähe des Plasmameniskus die
Form einer Hyperbel annehmen.
Für größere Radien der Plasmaelektrode
ist dann der Pierce-Rand ausreichend einen
laminaren Strahl zu gewährleisten.
Da der dünne Teil der Elektrode in kurzer
Zeit weg gesputtert wird, muss die Elektrode
am Plasmarand verstärkt werden.
Es gibt keine universelle Lösung wie
bei Elektronenkanonen.
WS2011/12
10.8
Extraktionssyteme:
Beim Design von Extraktionssystemen werden bestimmte Parameter, je nach Anwendung optimiert.
Im Allgemeinen gilt dies für den Strom oder die Emittanz. Wie wir gesehen haben weicht die
Charakteristik der Plasmaextraktion von der von Elektronenkanonen ab. Trotzdem sind folgende
Beziehungen experimentell überprüft:
1/ 2
⎛q⎞
I tr ∝ ⎜ ⎟
⎝ A⎠
I tr ∝> U 3 / 2
und
, wobei Itr der transportierte Strom durch das System ist.
Experimentell wurde ein entsprechend modifiziertes Child-Langmuir-Gesetz ermittelt:
I tr = P ⋅ U
*
3/ 2
S2
1 + aS 2
a= Abberationsfaktor
(a~3) und P* = Perveanzfaktor, welche sich für ideale
Systeme aus der Perveanz planarer Systeme wie folgt
berechnet
zu
P* =
4π
ε0
9
2 eq
mu A
.
Beispiele für gemessene Ströme zu verschiedenen
Akzeptanzwinkeln zeigt nebenstehende Graphik.
WS2011/12
10.9
Für den transportierten Strahl ist der Abberationsfaktor jedoch vom maximalen Divergenzwinkel
abhängig, der vom Extraktionssystem gerade noch akzeptiert wird. Für diese Systeme und unter
Berücksichtigung der Durchschlagsfestigkeit von Extraktionssystemen wird ein Aspektverhältnis von
0.5-0.6 empfohlen. Performance Limits liegen bei Systemen mit S = 1, P* = 6*10-5 [mA/V3/2] und
a = 1.7 wie nachfolgendes Beispiel zeigt.
Für den maximalen Strom durch ein solches System
bei dem ein Akzeptanzwinkel von ±20 mrad angenommen
wird ergibt sich dann durch
⎡
⎤
I tr , max = 0.703 ⋅ U 3 / 2 ⎢mA
3/ 2
⎣ (kV ) ⎥⎦
WS2011/12
10.10
Die Stromlimitierung ist nicht für alle Anwendungen
akzeptabel. Neutralinjektion in
Fusionsplasmen und Ionenantriebe benötigen
spezielle, maßgeschneiderte
Extraktionssysteme.
1) Das Diodenextraktionssystem ist das
simpelste Extraktionsschema, wenn die
Raumladungskompensation keine Rolle
spielt, denn Elektronen werden zum Plasma
zurück beschleunigt.
Æ Aufbrechen der Kompensation und
Anodenlinseneffekt
2) Das Triodenextraktionssystem ist das
einfachste Schema zum Erhalt der
Raumladungskompensation. Eine auf
negativem Potential liegende Schirmoder Screening-Elektrode (SE) vor der
Erdelektrode (EE) verhindert das
Aufbrechen der Kompensation und
entkoppelt die Einstellung der Strahlenergie
vom Extraktionspotential und reduziert
den Anodenlinseneffekt.
WS2011/12
10.11
3) Pentodenextraktionssystem (Two-gap-extraction system)
Hier unterstützt eine Formierungs- oder Puller-Elektrode
(PE) die Strahlformierung durch Anpassen des Piercerandes
(wie bei Wehneltelektrode) und die Schirmelektrode (SE)
ist zum stabileren Betrieb von zwei Erdelektroden umgeben.
Ein Beispiel für ein solches Extraktionssystem zeigt die
Nebenstehende Abbildung. Die Praxis zeigt, dass solche
Systeme nur für Extraktionsspannungen ab 50 kV Vorteile
Gegenüber „single gap“ Systeme zeigen.
Man unterscheidet noch Einloch- oder Mehrlochextraktion.
Um das Stromlimit für Einlochextraktionssysteme zu
Umgehen geht man zu Mehrloch- oder multi apertureSystemen über. Zwar leidet die Strahlqualität, also die
Emittanz darunter, trotzdem sind hohe Strahlströme
möglich.
7 Aperturen können hexagonal angeordnet werden
ohne, dass die Strahlqualität schlechter wird.
Es wurden Systeme mit bis zu 1000 Aperturen
realisiert und mit Strömen von Protonen von
bis zu 10-100 A betrieben.
Æ Problem: Kühlung der Gitter
WS2011/12
10.12
Für den minimalen theoretischen Divergenzwinkel α0 gilt:
⎡ 1.67 ⋅ P ⎤
α 0 = 0.5 ⋅ S ⋅ ⎢1 −
⎥
P
⎢⎣
planar ⎥
⎦
WS2011/12
mit
4
Pplanar = ε 0
9
2 eq
mu A
F
d2
F = Oberfläche Plasmameniskus
10.13
Bewegung geladener Teilchen in axialsymmetrischen Feldern
Bei der Strahlformierung und dem -transport in Elektronenkanonen und in Ionenquellen sind
axialsymmetrische Geometrien am häufigsten vertreten. Daher wird die Bewegungsgleichung in
Zylinderkoordinaten transformiert. In elektrischen und magnetischen Feldern ergibt sich die Bewegung
von geladenen Teilchen aus der Lorentzkraft:
In Zylinderkoordinaten (siehe Lehrbücher):
r r r
r&
&
m ⋅ r = q( E + v × B )
m ⋅ ( &r& − rθ& 2 ) = q( E r + rθ& ⋅ Bz − z& ⋅Bθ )
m ⋅ (rθ&& + 2r&θ&) = q ( E + z& ⋅ B − r& ⋅B )
θ
r
z
m ⋅ &z& = q( E z + r& ⋅ Bθ − rθ& ⋅B r )
In axialsymmetrischen Feldern:
Eθ = Bθ = 0 .
Außerdem gilt:
1 d 2&
( r θ ) = 2 r&θ& + rθ&&
r dt
m d 2&
&
&
&
&
⇒ m ⋅ ( rθ + 2 rθ ) =
(r θ ) = q ( z& ⋅ Br − r& ⋅B z ) , wobei m ⋅ r 2 ⋅ θ& = r ⋅ l
r dt
l ist der Drehimpuls des Teilchens um die Strahlachse! Für das Vektorpotential bei einem
axialsymmetrischen Magnetfeld muß gelten:
r
r
B = rot A, Bθ = 0 ⇒
WS2011/12
∂Ar ∂Az
=
∂z
∂r
∀Ar , Az
⇒
Ar = Az = 0
10.14
r
r
∂Aθ
1 ∂
A = (0, Aθ ,0) ⇒ B = ( −
,0,
( rAθ ))
r ∂r
∂z
Eingesetzt in die obige Gleichung ergibt dies:
⇒
∂A
∂ ( rAθ )
∂
d 2&
q
q d
( r θ ) = ( − r ⋅ z& ⋅ θ − r& ⋅
) = − ( ( rAθ ) − ( rAθ ))
dt
m
∂z
∂r
m dt
∂t
da wir nur statische Fokussierfelder betrachten ist die partielle Ableitung nach der Zeit Null. Damit
erhält man:
d
( mr 2θ& + q ⋅ r ⋅ Aθ ) = 0 ⇒ mr 2θ& + q ⋅ r ⋅ Aθ = const. = Pθ
dt
Pθ ist der generalisierte Impuls der θ-Komponente. Für den magnetischen Fluss gilt:
r r
r r
Φ = ∫ B ⋅ dF = ∫ rotA ⋅ dF =
F
F
r r
∫ A ⋅ ds
(F )
2π
Æ
Φ (r ) = ∫ rAθ dθ = 2π rAθ
0
Damit nimmt der generalisierte Impuls die folgende Form an:
WS2011/12
10.15
q ⋅ Φ(r)
Pθ = Pθ 0 = m r 2θ& +
= const. ⇒
2π
2
r
q
θ& = 02 θ&0 +
( Φ 0 ( r0 ) − Φ ( r ))
2
r
2π ⋅ m ⋅ r
Das ist das sogenannte Busch-Theorem (Drehimpulserhaltung)!
Für ein Solenoidfeld erhält man: Bz = const Æ
Φ ( r ) = Bz ⋅ π ⋅ r 2
Damit nimmt das Busch-Theorem die folgende Form an:
2
2
r
q
r
⇒ θ& = 02 θ&0 +
( 02 B0 z − Bz )
r
2m r
q
&
Bz
Sind die Winkelgeschwindigkeit θ&0 und das Magnetfeld B0 z am Startpunkt Null, dann ist θ = −
2m
und damit identisch mit der Lamorfrequenz. Wenn also Teilchen aus einer feldfreien Zone in eine
Magnetfeld eingeschossen werden, dann gyrieren diese mit der Lamorfrequenz ωL = ωc/2.
Damit lauten die Bewegungsgleichungen für
θ&0 = 0
2
q
r
0
&
( 2 B 0 z − Bz ) , m ⋅ &z& = q( E z − rθ& ⋅B r )
m ⋅ ( &r& − rθ& 2 ) = q( E r + rθ& ⋅ Bz ) , θ =
2m r
WS2011/12
10.16
Setzt man nun die mittlere Gleichung in die beiden anderen ein, so erhält man die
Randstrahlgleichung
2
2
q ⎞ r04 B02z ⎛ q ⎞ 2
q
⎛
&r& = E r + ⎜
−⎜
⎟
⎟ Bz r
3
m
⎝ 2m ⎠ r
⎝ 2m ⎠
Der erste Term beschreibt den Kraftanteil der Raumladung, der zweite die Zentrifugalkraft oder
magnetische Emittanz und der dritte Term beschreibt die Fokussierkraft des Magnetfeldes. Für die zAbhängigkeit erhält man analog:
q r02
m ⋅ &z& = qE z − qr
( 2 B0 z − Bz ) ⋅B r
2m r
Wenn man die Bewegung der Randstrahlteilchen in Abhängigkeit von z darstellen möchte, dann muss
man die obigen Gleichungen kombinieren:
⎡q
q2
2
v z r ′′ + ⎢ E z −
2
m
m
2
⎣
2 4 2
2
⎞ ⎤
⎛ r02
q
q
r
B
q
⎞ 2
⎛
⎞ 0 0z ⎛
−
r ⎜⎜ 2 B0 z − Bz ⎟⎟ Br ⎥ ⋅ r ′ = E r + ⎜
⎜
⎟ Bz r
⎟
3
m
⎝ 2m ⎠ r
⎝ 2m ⎠
⎠ ⎦
⎝r
Die ist die Paraxialgleichung. Wenn Ez = 0 und Br << Bz, dann ist der Term in r’ zu vernachlässigen.
Br sorgt für eine Änderung von vz und damit von Wkin||. Damit wandelt also Br kinetische Energie von
der longitudinalen Bewegung in die transversale, wie wir es beim magnetischen Spiegel schon kennen
gelernt haben.
WS2011/12
10.17
Die Paraxialgleichung mit Raumladung (betrifft nur Er) lautet daher:
⎡q
q2
2
v z r ′′ + ⎢ E z −
2
m
m
2
⎣
2 4 2
2
⎞ ⎤
⎛ r02
q
I
q
r
B
q
⎞ 2
⎛
⎞ 0 0z ⎛
+⎜
−
r ⎜⎜ 2 B0 z − Bz ⎟⎟ Br ⎥ ⋅ r ′ =
⎟
⎜
⎟ Bz r
3
m
v
r
m
r
m
r
2
πε
2
2
⎠
⎝
⎠
⎝
⎠ ⎦
⎝
0 z
Beispiele (ohne Raumladung): Î Magnetische Solenoidlinse
Bz
B0z = Ez = 0
⎡ q2
⎤
q
I
⎛ q ⎞ 2
2
−⎜
v z r ′′ + ⎢ 2 rBz Br ⎥ ⋅ r ′ =
⎟ Bz r
m 2πε 0 v z r ⎝ 2m ⎠
⎣ 2m
⎦
2
z1
z2
z
Im Integral von z1 bis z2 werden sich die Effekte von Br weitgehend aufheben, da das Feld
symmetrisch in z ist. Man kann nun die obige DGL numerisch mit Raumladung lösen oder ohne
Raumladung analytisch behandeln:
2
⎛ q ⎞ 2
v r ′′ + ⎜
⎟ Bz r = 0 ⇔ r ′′ + k ⋅ r = 0
⎝ 2m ⎠
2
z
Hillsche Differentialgleichung
Dieser Typ von DGL bildet die Grundgleichung der linearen Strahloptik! Integration der Gleichung:
WS2011/12
10.18
dr
dz
z2
z1
2
⎛ q ⎞ 1
= −⎜
⎟ 2
m
2
⎝
⎠ vz
z2
q2
r0
B
r
dz
≈
−
∫z1
8m q ⋅ U acc
2
z
z2
dr
dz
∫ B dz
2
z
=0
z1
dr
dz
z1
z1
z2
f
z2
z
Hier wurde eine dünne Linse angenommen. Daher bleibt der
Strahlradius r0 in der Linse nahezu konstant. Für die
Geschwindigkeit kann man noch die Beschleunigungsspannung
dr
Uacc einsetzen.Damit erhält man für die Fokallänge: dz
z2
r
≈ 0
f
q2
1
=−
f
8mq ⋅ U acc
⇒
z2
2
B
z
∫ dz
z1
z2
Mann nutzt in der linearen Strahloptik eine effektive Feldlänge zL mit
B02 z L = ∫ Bz2 dz
Nun gyrieren geladene Teilchen im Soleniodfeld. Nach dem Busch Theorem ist
mit
θ& =
WS2011/12
dθ dθ
=
vz
dt
dz
z1
θ& = −
.
q
Bz .
2m
folgt dann für die Winkeländerung mit dem Ort:
10.19
q
dθ
q
Bz = −
Bz
=−
2m ⋅ vz
dz
8mqU acc
q
⇒ θ =−
8mqU acc
z2
∫ B dz
z
z1
Neben den radial wirkenden Kräften
gibt es auch azimuthal wirkende Kräfte,
die zu einer Winkeländerung in diese
Richtung führen
Die Änderung des Winkels hängt vom Vorzeichen der Ladung und der Richtung des Magnetfeldes ab.
Vorteile der Solenoidlinsen sind die Erhaltung der Raumladungskompensation und das Fehlen der
sphärischen Abberation. Nachteile sind die Beschränkung auf niederenergetische Strahlen und die
chromatische Abberation.
Elektrostatische Zylinderlinsen
Bz = Br = 0 ,
q
⎡q ⎤
vz2 r ′′ + ⎢ Ez ⎥ ⋅ r ′ = Er
m
⎣m ⎦
Ziel hierbei ist es die Felder mit den Potentialen auszudrücken:
WS2011/12
v z2 =
2qU acc
m
10.20
r ′′ +
Er
Ez
′
⋅r −
=0
2U acc
2U acc
∂V
∂V
, Er = −
, Eθ = 0 und
Ez = −
∂r
∂z
∂ 2V 1 ∂V ∂ 2V
∆V = 2 +
+ 2 =0
∂z
r ∂r ∂r
Für axialsymmetrische Probleme kann man das Potential entwickeln:
1 2 ∂ 2V ( z,0) 1 4 ∂ 4V ( z,0)
+ ...
V ( z , r ) = V ( z,0) + r
+ r
2
4
∂r
∂r
2
24
mit der Laplacegleichung erhält man
Nun gilt außerdem:
1 2 ∂ 2V ( z,0) 1 ∂V ( z,0)
V ( z , r ) ≈ V ( z ,0) − r
− r
2
∂z
∂r
2
2
∂V
1 2 ∂ 2V
1 2 ∂ 2V ( z,0)
r
=− r
⇒ V ( z, r ) ≈ V ( z,0) − r
2
∂r
2 ∂z
∂z 2
4
Damit ergeben sich die elektrischen Feldstärken zu
∂V
∂V 1 ∂ 2V 1
Ez = −
= −V ′, E r = −
= r 2 = rV ′′
∂z
∂r 2 ∂z
2
Die Bewegungsgleichung in elektrostatischen Rohrlinsen ergibt sich damit zu
WS2011/12
10.21
r ′′ +
V′
V ′′
′
⋅r +
r = 0 mit U acc = U 0 + V
2U acc
4U acc
d ⎛
dr ⎞
r
V ′′
=
−
U
V
+
⎟
⎜ 0
dz ⎝
dz ⎠
4 U0 + V
dr
U0 + V
dz
z2
z1
dr
dz
⇒
=0
z1
dr
dz
z1
z2
z2
f
f
z
r
V ′′
4 U0 + V
z1
z2
= −∫
1
=
f
1
r0 U 0 + V
1
1 dr
=−
f
r0 dz
r
V ′′
∫z1 4 U 0 + V dz
z2
z2
Das Integral lässt sich schreiben als:
r V ′′
r0
dz
≈
∫z1 4 U 0 + V
4
z2
z2
∫
z1
V ′′
r0 ⎡ V ′
dz = ⎢
4 ⎢⎣ U 0 + V
U0 +V
z2
⎤
r0
+
⎥
⎥⎦ z1 8
z2
∫ (U
z1
(V ′)2
+V )
3/ 2
0
dz
Spezialfälle:
WS2011/12
10.22
A) Einzellinse
Vz1 = Vz2 = 0
dr
dz
z2
z2
z2
⎞
⎛
r0 ⎜ ⎡ V ′ ⎤
1
(V ′) 2
⎟
dz
=−
+ ∫
⎢
⎥
3/ 2
⎟
4 U 0 ⎜ ⎢⎣ U 0 ⎥⎦ z1 2 z1 (U 0 + V )
⎠
⎝
Sind die Feldstärken
z1
z2
z
VE
Vz′1 = Vz′2 = 0 , dann erhält man für die Brennweite
1
1
=−
f
8 U0
(V ′) 2
∫z1 (U 0 + V )3 / 2 dz
z2
Dies bedeutet das Einzellinsen immer Sammellinsen sind, da alle Größen in der Gleichung positiv
sind. Bei Strahlen mit hoher Raumladung besitzen diese Linsen den Nachteil, dass diese die
Raumladungskompensation brechen.
B) Diaphragma
1
1
=
f r0 U 0 + V
WS2011/12
r V ′′
∫z1 4 U 0 + V dz
z2
10.23
Da z1 Æ z2 geht gilt:
1
1
≈
f r0 U 0 + V
1
4 U0 +U2
U2
U1
r0
V ′′
∫z1 4 U 0 + V dz =
z2
Vz′2 − Vz′1
1
(Vz′2 − Vz′1 ) ,
≈
U 0 + U 2 4U 0
z1
z2
z
wenn U2 = 0
Die Brennweite ist dabei proportional zur Differenz der Feldstärken im Raum vor und hinter der
Blende. Ist
Vz′1 = E1 ≥ Vz′2 = E2 ,
was im Falle einer Anodenanordnung (E2=0) vorliegt, dann ist f
negativ. Damit ist eine Anodenblende eine Zersteuungslinse und zwar für alle Extraktionssyteme. Man
nennt diesen Effekt den Anodenlinseneffekt.
f ≈−
WS2011/12
4U 0
4U 0
=−
E1
E Anode
10.24