4) Magnetischer Einschluss von Plasmen

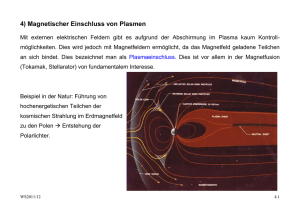
4) Magnetischer Einschluss von Plasmen
Mit externen elektrischen Feldern gibt es aufgrund der Abschirmung im Plasma kaum Kontrollmöglichkeiten. Dies wird jedoch mit Magnetfeldern ermöglicht, da das Magnetfeld geladene Teilchen
an sich bindet. Dies bezeichnet man als Plasmaeinschluss. Dies ist vor allem in der Magnetfusion
(Tokamak, Stellarator) von fundamentalem Interesse.
Beispiel in der Natur: Führung von
hochenergetischen Teilchen der
kosmischen Strahlung im Erdmagnetfeld
zu den Polen Æ Entstehung der
Polarlichter.
WS2011/12
4.1
Zunächst betrachten wir die Bewegung von Einzelteilchen im Magnetfeld. Berücksichtigen wir
kollektive Effekte, dann müssen diese durch die Magnetohydrodynamik (MHD) beschrieben werden.
r r
r& r
m ⋅ v = FL = q ⋅ v × B
Lorentzkraft:
r
r
FL ⊥ B
r&
m ⋅ v|| = 0 ,
Wegen
ist
d.h. das Magnetfeld hat keinen Einfluss auf die Bewegung parallel
zum Magnetfeld. Außerdem ändert sich nur die Richtung von der Geschwindigkeit senkrecht zum
Magnetfeld, die kinetische Energie des Teilchens ändert sich dabei nicht (Kreisbahn).
v⊥2
m ⋅ = mω c2 r = q ⋅ v⊥ ⋅ B = qω c r ⋅ B
r
Æ
ωc =
q
B
m
Zyklotronfrequenz
ω ce [Hz ] = 1.76 ⋅1011 ⋅ B[T ] , ω ci =
WS2011/12
(4.1)
me
ω ce ,
mi
4.2
Radius auf Orbit:
r=
m ⋅ v⊥
q⋅B
• Gyrationsbewegung der Elektronen Æ Plasmadiagnostik
• Einstrahlen einer elektromagnetischen Welle mit ω = ωce Æ Plasma heizen
Mit
1
2
m ⋅ v⊥2 = kT
(2 Freiheitsgrade senkrecht zu B) folgt der Lamorradius rL zu
Te [eV ]
m ⋅ v⊥
2mkT
−6
[m]
rL =
=
= 3.4 ⋅10 ⋅
q⋅B
qB
B[T ]
(4.2)
Beispiel: Te = 1 eV, B = 1 T → rL = 3.4 µm
Was ist jedoch, wenn
r r
r& r
m⋅v = F + q⋅v × B
mit einer zusätzlichen Kraft F, welche auf die Teilchen wirkt
> keine geschlossenen Kreisbahnen mehr
WS2011/12
4.3
Für räumlich und zeitlich konstantes B und F
Æ guiding center-Ansatz
Bewegung des Führungszentrums
r r
r r r
r m⋅v v × B
m r r
rc = r + rg , rg =
⋅
=
v×B
2
q⋅B v⋅B q⋅B
Die Geschwindigkeit des Führungszentrums ist
r
r r r
r r& r& r& r
m r& r r
1
vc = rc = r + rg = v +
⋅v × B = v +
( F + q ⋅ v × B) × B
2
2
q⋅B
q⋅B
mit
r r r r r r
r
r
( v × B ) × B = ( v ⋅ B ) B − B 2 v = − B 2 v⊥
r r
r r F ×B
vc = v|| +
q ⋅ B2
folgt für die Geschwindigkeit des Führungszentrums
mit
r
r&
mv|| = F||
(4.3)
Der zweite Term ist die Driftgeschwindigkeit, die nicht beschleunigt und senkrecht zu B und F| steht.
WS2011/12
4.4
Beispiele:
Æ
1.)
elektrisches Feld
r
r
F = q⋅E
Æ
E x B –Drift
v r
r
E×B
vD =
B2
Die Driftgeschwindigkeit
ist ladungsunabhängig!
2.)
Gravitationskraft
r
r
F = m⋅g
Æ
Das Teilchen gewinnt Energie in Richtung
Ladungstrennung mit dem Strom
r r
r
m⋅g × B
vD =
q ⋅ B2
r
g|| .
Die Drift ist ladungsabhängig und führt zur
r r
r
r r
g × B ⎛ mi
⎞
m
+
j g = n e e ⋅ ( vi − v e ) = n e e
⎜
e⎟
e ⋅ B2 ⎝ Z
⎠
Für Quellen ist diese Drift jedoch vernachlässigbar. Wichtiger sind Driften aufgrund von Gradienten.
WS2011/12
4.5
3.)
r r
r
∇ B-Drift, wenn B = f ( x, t )
Æ Krümmungsdrift
r r
∇⋅ B = 0
Aufgrund von
bedingt ein Gradient in
B eine Krümmung der Feldlinien. Dies bewirkt die
r2
r
v|| r
F = m⋅
⋅ rˆc
Zentrifugalkraft
.
Rc
r 2 r r
m
v
⋅
r
rˆc × B
||
vD =
⋅
Rc
q ⋅ B2
r
rˆ
rˆ
rc dT
∇B
=
=−
Nun gilt: R
ds
B
c
Die Zentrifugalkraft zeigt in Richtung
r
− ∇B und damit
r 2
r
r
m
v
⋅
r
||
vD = −
⋅ ∇B × B
3
q⋅B
Beispiel: toroidales Magnetfeld
WS2011/12
4.6
Adiabatische Invarianz des magnetischen Moments
Ein geladenes Teilchen bildet einen Kreisstrom im Magnetfeld
I =q
v
2π ⋅ r
=q
ω
2π
magnetisches Dipolmoment:
r
r
r
q2
2 r
1
µ m = I ⋅ ∫ dF ⋅ n F = I ⋅ F ⋅ n F = 2 qω c ⋅ rL ⋅ n F =
B ⋅ rL2 ⋅ n F
2m
F
r
mit dem Lamorradius
v m
rL = ⊥
B⋅q
2
⎛ v⊥ m ⎞
q
m ⋅ v ⊥2 W⊥
B ⋅ ⎜⎜
µm =
=
⎟⎟ =
B
2m ⎝ B ⋅ q ⎠
2B
2
erhält man
(4.4)
Wie ändert sich nun das magnetische Moment bei einer langsamen Drift des Führungszentrums?
Änderung des magnetischen Flusses durch die Orbitfläche! (Induktion)
Mit der Gyrationsperiode
Æ
τC =
2π
ωc
und
∆W⊥ = q ⋅
dW⊥ ∆W⊥ π ⋅ q ⋅ rL dB
dB
≈
⋅
= µm
=
τc
dt
τc
dt
dt
WS2011/12
dφ
dB
= π ⋅ q ⋅ rL2 ⋅
dt
dt
wenn τc und rL eingesetzt werden.
4.7
Andererseits ist
dµ m
dB
dW⊥ d
= (µm B) = B
+ µm
dt
dt
dt
dt
daher gilt:
dµ m
= 0 , µ m = const .
dt
Das magnetische Moment bleibt bei einer langsamen Driftbewegung (langsam ggü. der Gyrationsbewegung) erhalten.
Æ
Beispiel:
adiabatische Invariante
magnetischer Spiegel
Läuft ein Teilchen in ein Gebiet höherer Feldstärke
so nimmt wegen der Konstanz des magnetischen
Moments auch die kinetische Energie der
Gyrationsbewegung zu. Da die Gesamtenergie der
Teilchen erhalten bleiben muss, nimmt die kinetische
Energie in Richtung der Magnetfeldlinien ab.
Um v|| komplett abzubauen muss gelten:
µ m ( Bmax − B1 ) = ∆W⊥ = W2 ⊥ − W1⊥ > W||,1
Dabei startet das Teilchen an Position 1. Position 2 bezeichnet das Magnetfeldmaximum Bmax.
WS2011/12
4.8
B2 W2 ⊥
∆W⊥
=
= 1+
B1 W1⊥
W1⊥
⇒
B2
∆W⊥
−1 =
≥
B1
W1⊥ W1⊥
W||,1
2
⎛ v1|| ⎞
⎟⎟ = (cot α )2
= ⎜⎜
⎝ v1⊥ ⎠
Man bezeichnet B2/B1 als das Spiegelverhältnis.
α
v 1⊥
v 1 ||
Der Verlustkegel ergibt sich aus
Bmin
α = arcsin(
)
Bmax
(4.5)
Die obige Gleichung zeigt, dass ein magnetischer Spiegel nicht perfekt reflektiert. Vor allem Teilchen
mit keiner Geschwindigkeitskomponente senkrecht zum Magnetfeld gehen verloren (da deren Winkel
bezüglich der Achse kleiner als α ist.
WS2011/12
4.9
Magnetischer Einschluss findet sich im Ionenquellenbereich wie folgt wieder:
•
•
•
•
Elektron Zyklotron Resonanz Ionenquelle (EZR) (resonantes Heizen von Plasmen mit HF)
Einschuss von Ionen in eine Elektronenstrahl-Ionenquelle (EBIS)
Multicusp-Ionenquellen
Bewegung von Ionen in einer EBIS und einer Penningfalle
WS2011/12
4.10