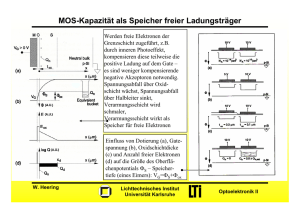
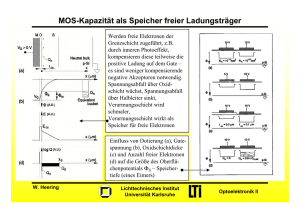
Elektronik für Plasma- und Laserlichtquellen - KIT

Maxwell- und Materialgleichungen
JG
JG
∂B
rotE = −
∂t
JG
divB = 0
JG
JG ∂ D G
+j
rotH =
∂t
JG
divD = ρ
JG
JG
D = ε0ε r E
JG
JG
B = µ 0µ r H
G
JG JJG
j = σE + jext
JG
E
JG
H
JG
D
JG
B
G
j
elektrische Feldstärke
magnetische Feldstärke
elektrischeVerschiebungsdichte
magnetische Flussdichte
elektrische Stromdichte
Materialgleichungen für isotropes Medium: rel.
Permittivität εr, rel. Permeabilität µr und el.
Leitfähigkeit σ sind Materialkennzahlen – hier
keine Tensoren
JG
JG
JG
JG
JG
∂
Rotation angewandt auf ∇ × (∇ × E) = ∇ (∇ ⋅ E) − ∇ E = −∆ E = −µ
rotH ⇒
1. Maxwell-Gleichung:
∂t
2
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Wellengleichung
G
G
2
G
∂ E
∂E
∆E − ε ⋅µ 2 − σ ⋅µ
=0
∂t
∂t
ε = ε 0 ε r , µ = µ 0µ r
c = 1/ ε0µ 0
Wellengleichung der elektrischen Feldstärke E,
abzuleiten aus den Maxwell-Gleichungen und
Materialgleichungen für ein homogenes,
isotropes Dielektrikum ohne Raumladungen;
c Vakuumlichtgeschwindigkeit, σ „optische“
Leitfähigkeit
G
ρ = 0 → divE = 0
G
G
E = {E x , 0, 0} , q = {0, 0, q z }
Lösung muss transversale Welle mit Feldvektor
senkrecht zum Ausbreitungsvektor sein!
O.B.d.A.: linear polarisiert
E x = E 0 e j( ω⋅t −qz ⋅z)
Lösungsansatz ergibt eingesetzt in Wellenglg.
Einführung einer komplexen
Brechzahl n* - Verknüpfung mit
komplexer Wellenzahl qz
E x = E0 e
W. Heering
ω
− k ⋅z
c
e
Phase
n
jω ( t − z )
c
(1)
q z 2 = εµω2 − jσµω
(2)
qz ≡
ω
c
c
⇒ v ph =
n
n * mit n* = n − jk
Lichttechnisches Institut
Universität Karlsruhe
⇒
Phasengeschwindigkeit
Optoelektronik II
Verknüpfung elektrischer Materialgrößen mit optischen Kennzahlen
Vergleich von (1) mit (2) ergibt:
(3)
n 2 − k 2 = εµ ⋅ c 2 = ε r ⋅ µ r
n reelle Brechzahl
k Absorptionszahl
(4)
σ ⋅ c2
2n ⋅ k =
µ
ω
n2=εr für k =0 und µr=1 – Maxwell-Beziehung
ω
Bestrahlungsstärke
−
2
k ⋅z
ω
2
2
Absorptionskoeffizient
c
⇒a=2 k
E x ∝ E0 e
ist proportional
c
Einführung einer komplexen dielektrischen Funktion ε*:
n *2
⇒
ε * = ε1 − jε 2 =
2
µ ⋅c
(5)
(6)
n2 − k 2
=ε
ε1 =
2
µ ⋅c
2n ⋅ k σ
=
ε2 =
2
µ ⋅c ω
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Kramer-Kronig-Dispersionsrelation
∞
2 ω ' ε 2 (ω ')
dω '
ε1 (ω) = 1 + P ∫ 2
2
π 0 ω' − ω
∞
ε1 (ω ')
2
dω '
ε 2 (ω) = P ∫ 2
2
π 0 ω' − ω
P Cauchyscher Hauptwert
des Integrales bei der
Singularität ω‘= ω
n und k wie auch ε1 und ε2 sind nicht unabhängig von einander,
sondern über die Kramer-Kronig Dispersionsrelation mit einander
verknüpft!
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Polarisierbarkeit – Übergang von der makroskopischen zur
mikroskopischen Beschreibung
Die ins Material eindringende el.magn. Welle polarisiert die Atome bzw. Moleküle.
Polarisation:
P = N p = Nα ⋅ Elok ≈ Nα ⋅ E
D = ε * ⋅E = ε 0 E + P
p
mittleres induziertes Dipolmoment
N Anzahldichte der Atome bzw. Moleküle
Elok lokales (mikroskopisches) el. Feld ≈ äußeres (makroskopisches) el. Feld
- gute Näherung bei nicht gebundenen Elektronen
α komplexe Polarisierbarkeit - berechnet aus einem atomaren Modell
D komplexe dielektrische Verschiebungsdichte
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Polarisierbarkeit und optische Kennzahlen
E = Elok
⇒
Mit µc2=µr/ε0
folgt aus (5), (6) und (7)
W. Heering
ε * = ε1 − jε 2 = (1 +
n − k = Re(1 +
2
2
Nα
N ⋅α
ε0
(7)
)µr
ε0
Nα
2nk = − Im(1 +
) µr
ε0
Lichttechnisches Institut
Universität Karlsruhe
)ε 0
(8)
Optoelektronik II
Lorentz-Oszillator
Lorentz-Modell
anwendbar auf Halbleiter und Isolatoren
quantenmechanisch verallgemeinerbar
beschreibt durch elektrisches Feld Elok erzwungene Schwingung eines an ein Atom
gebundenen Valenzelektrons mit Ladung e und Masse m - anstelle der reduzierten Masse kann
Elektronenmasse eingesetzt werden, weil real das Elektron gegen das sehr viel schwerere Kristallgitter schwingt:
d2r
dr
2
m 2 + mΓ
+ mω 0 r = − e Elok
dt
dt
beschleunigende, dämpfende, rücktreibende,
Mit
antreibende Kraft
Elok (t ) = Elok (0)e jωt
Der 2-te Term der DGL beinhaltet den
Energieverlust durch viskose Dämpfung, der
3-te Term ist gemäß dem Hookschen Gesetz.
erhält man durch Einsetzen in obige DGL
−e/m
r (t ) =
Elok (t )
2
2
(ω0 − ω ) + jΓω
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Dispersionsgleichungen
p = − e r = α (ω ) Elok ⇒
e2
1
α (ω ) =
m (ω 0 2 − ω 2 ) + jΓω
(9)
Mit (7) und (9) bzw. (7) und (8)
e2 N
1
ε * / ε0 = 1 +
mε 0 (ω0 2 − ω 2 ) + jΓω
(10)
e2 N
ω0 − ω 2
ε1 / ε 0 = n − k = 1 +
mε 0 (ω0 2 − ω 2 ) 2 + Γ 2ω 2
2
2
2
e2 N
Γω
ε 2 / ε 0 = 2nk =
mε 0 (ω 0 2 − ω 2 ) 2 + Γ 2ω 2
W. Heering
(11)
Lichttechnisches Institut
Universität Karlsruhe
für nichtmagnetische
Materialien: µr=1
Optoelektronik II
Dielektrische Funktion für Ensemble klassischer Atome mit 1 Elektron
Normale Dispersion: ε1 wachsend mit ω
e2 N
mε0 ω0 Γ
Anormale Disprsion: ε1 fallend mit ω im
Dämpfungsbereich
Dämpfungs (Absorptions)profil für
ω − ω0 << ω0
e2 N
1
ε2 / ε0 ≈
mε 0ω 0 Γ 1 + ( ω − ω 0 ) 2
Γ/2
ε1 ⇒ ε1 / ε 0
ε2 ⇒ ε2 / ε0
W. Heering
Lorentzprofil mit Halbwertsbreite Γ
und Dämpfungsmaximum bei ω0
(ε 2 / ε 0 ) max ≈
Lichttechnisches Institut
Universität Karlsruhe
e2 N
mε 0ω 0 Γ
Optoelektronik II
Verallgemeinerung auf mehrere quantenmechanische Oszillatoren
Dielektrische Funktion für Ni Atome pro Volumeneinheit mit Übergangsenergie =ωi
zwischen zwei atomaren Zuständen und relativer Übergangswahrscheinlichkeit fi
(Oszillatorenstärke)
e2
N i fi
ε * / ε0 = 1 +
∑
mε 0 i (ωi 2 − ω 2 ) + jΓiω
N = ∑ Ni
i
Summenregel
1 = ∑ fi
i
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Polarisationsformen
Orientierung
permanenter
Dipole - MW
IonengitterSchwingungen
– MIR + FIR
Auslenkung gebundener
Elektronen – NIR + VIS + UV
Realteil der Polarisierbarkeit als Funktion der Frequenz:
Im Bereich optischer Frequenzen, vor allem im Bereich ©, ist der Beitrag der Orientierungspolarisation wie auch der der Atompolarisation wegen der Trägheit der Dipole und der Atome
(Ionen) klein gegen den der Elektronenpolarisation.
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Spektrale Abhängigkeit der dielektrischen Funktion
Beispiel:
=ω0 = 4eV
=Γ = 1eV
Ne 2
= 60
mε0
ε1 ⇒ ε1 / ε 0
ε2 ⇒ ε2 / ε0
W. Heering
Einsatz von
Spektralbereich IV: ε1 / ε0 = 0
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Spektrale Abhängigkeit von Brech- und Absorptionszahl
n und k berechnet aus der dielektrischen
Funktion:
1
⎡⎣(ε12 + ε 2 2 )1/ 2 + ε1 ⎤⎦ / ε 0
n=
2
1
⎡⎣(ε12 + ε 2 2 )1/ 2 − ε1 ⎤⎦ / ε 0
k=
2
Einsatz von
Spektralbereich IV: n = k =
ε2
2ε 0
Bereich I und IV: Medium nahezu
transparent
Bereich II: Medium stark absorbierend
Bereich III: Medium reflektierend
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Spektrale Abhängigkeit der Reflexion
Fresnel-Reflexionsgrad bei
senkrechtem Einfall aus Medium mit
Brechzahl n=1 (Vakuum, Luft,..)
(n − 1) 2 + k 2
R=
(n + 1) 2 + k 2
Bereich III:
Weit oberhalb der Resonanzfrequenz, wo
n≠1 und k relativ groß ist, starke
Reflexion.
Photonenenergie>Bindungsenergie der
Elektronen – Elektronen quasi frei,
Isolator mit „metallischer“ Reflexion. Für
gute Isolatoren wie die Alkalihalogenide
liegt Bereich III im VUV, für Halbleiter
wie Ge und Si mit Bandkante im IR liegt
Bereich metallischer Reflexion im VIS.
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Diskussion des Lorentz-Modells
Bereich I:
Wenn ω << ω0 ⇒ ε 2 / ε 0 = 2nk → 0 ⇒
Schwache
Absorption
k ≈ 0 ⇒ ε1 / ε0 ≈ n 2
Beispiele
KCl: n=1,5 in I, folglich hohe Transparenz im Gebiet I
Si: 4 Valenzelektronen / Atom; damit folgt aus (11) mit unten
2
stehender Übergangsfrequenz für ω → 0 ε1 / ε 0 ≈ n = 15 ,
also n=3,87 – tatsächlich n=3,5 im Niederfrequenzbereich
Ge: n=4 im Gebiet I, wegen der großen Brechzahl wie bei Si
nennenswerte Reflexion im Bereich I, obwohl keine
Absorption dort stattfindet
Bereich II:
Dielektrische Funktion und Reflexionsgrad
von Si; E 0 = =ω0 ≈ 3eV ⇒ ω0 ≈ 4,5 ⋅1015 s −1
W. Heering
Hohe Absorption, aber auch nennenswerte Brechzahlen und
damit auch beträchtliche Reflexion
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Plasmafrequenz
Bereich IV:
Einsatz von IV: ε1=0 bzw. n=k
ω >> ω0 >> Γ ⇒
Nahezu freie Elektronen, schwache Dämpfung;
Für
n = k ⇔ ε1 = 0
Damit folgt aus (11)
(12)
Ne 2
ω = ωp =
mε0
Plasmafrequenz – liegt im UV oder VIS
Oberhalb der Plasmafrequenz mit zunehmender Frequenz abnehmende Reflexion!
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Drude-Modell der Metalle
Quasifreie Elektronen im Leitungsband von Metallen – Übergang vom LorentzModell zum Drude-Modell durch Ansetzen der rücktreibenden Kraft gleich Null:
(11)
ω0 = 0 ⇒
Ne 2
1
ε1 / ε 0 = 1 −
mε0 ω2 + Γ 2
Ne 2
1
ε 2 / ε0 =
mε0 ω(ω2 + Γ 2 )
(12)
ε1 / ε0 = 1 −
⇒
ε 2 / ε0 =
W. Heering
ωp 2 τ2
1 + ω2 τ2
ωp 2 τ
In Metallen (viskose) Dämpfung durch
Stöße der Elektronen mit dem Gitter -
Γ = 1/ τ
τ ≈ 10−14 s
mittlere Zeit zwischen zwei Stößen
Metalle sollten sich optisch verhalten wie
Isolatoren im Bereich IV: ω >> ω0 >> Γ
ω(1 + ω2 τ2 )
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Dielektrische Funktion von Metallen
Im Bereich nahe der Plasmafrequenz:
ωτ >> 1 ⇒
ε1 / ε0 = n 2 − k 2 = 1 −
ωp 2
ω2
Insbesondere dicht oberhalb der Plasmafrequenz:
n >> k ⇒
n2 ≈ 1−
Siehe folgendes Bild!
ωp 2
ω2
=ωp = 5,5eV, =Γ = 0, 02eV
Bei der Plasmafrequenz verschwindet die Brechzahl,
die Phasengeschwindigkeit c/n und die Wellenlänge
λVak/n werden folglich unendlich groß – alle
Elektronen schwingen in Phase!
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Optische Eigenschaften von Metallen
Hohe Absorption und Reflexion unterhalb der Plasmafrequenz, meist im VIS, immer im IR!
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II
Lichttechnik-Tage in Karlsruhe – LTiK 2005
Montag, 7.11.2005
11.00 – 17.00 Uhr
Firmenkontaktmesse
Teilnehmende Unternehmen z.B.
BMW, Audi, VW und viele andere.
11.30 – 12.00 Uhr
Vorstellung Studienmodell 10
„Optische Technologien“
Lichttec
Prof.
Uli Lemmer
12.00 – 14.00 Uhr
Firmenpräsentationen im LTI-Hörsaal
15.30 – 16.30 Uhr
Stunde der „Offenen Labore“ im LTI
Ab 17.00 Uhr
Abendveranstaltung im HSI-Hörsaal
W. Heering
Lichttechnisches Institut
Universität Karlsruhe
Optoelektronik II