Pruning Pruning

Pruning
Overfitting vermeiden durch nachträgliches
Verkleinern (Pruning):
• Abschneiden eines Zweiges Tt für einen inneren Knoten t.
• Neues Label von t: häufigstes Konzept der Beispiele in D(t).
label(t) = argmaxi{|{(x, c(x)) ∈ D(t) : c(x) = i}|}
outlook
overcast
sunny
rain
yes
wind
temp.
strong
weak
yes
cool
hot
no
yes
no
t
mild
wind
weak
Tt
no
strong
yes
label(t) = No
Uwe Bubeck
Machine Learning: Decision Trees
1
Pruning
Overfitting vermeiden durch nachträgliches
Verkleinern (Pruning):
• Abschneiden eines Zweiges Tt für einen inneren Knoten t.
• Neues Label von t: häufigstes Konzept der Beispiele in D(t).
label(t) = argmaxi{|{(x, c(x)) ∈ D(t) : c(x) = i}|}
outlook
overcast
rain
yes
no
wind
weak
yes
sunny
strong
no
label(t) = No
Uwe Bubeck
Machine Learning: Decision Trees
2
1
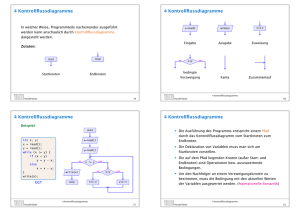
Reduced Error Pruning 1/4
• Aufteilen der Beispiele in Trainingsmenge D und
Validierungsmenge DV.
→ Allgemeine Technik zur Fehlerabschätzung
→ Probleme (bei kleiner Beispielmenge):
Kostbare Trainingsinformation geht verloren.
Sind die Klassen in D und DV gleich verteilt?
• Pruning innerer Knoten t mit Error(DV,T) ≥ Error(DV,T\Tt).
• In welcher Reihenfolge wählen wir solche Knoten?
→ Greedy-Ansatz:
Knoten mit größtem Verbesserungspotential
argmaxt{Error(DV,T) - Error(DV,T\Tt)}
Uwe Bubeck
Machine Learning: Decision Trees
3
Reduced Error Pruning 2/4
Finden des Knotens mit dem größten Verbesserungspotential:
Laut Skript ist Error die relative Missklassifikationsrate.
Wir können auch die absolute Fehlerzahl Failures benutzen:
argmaxt{Error(DV,T) - Error(DV,T\Tt)}
= argmaxt{Error(DV,T) ⋅ |DV | - Error(DV,T\Tt) ⋅ |DV |}
= argmaxt{Failures(DV,T) - Failures(DV,T\Tt)}
Dann gilt:
Failures(DV,T) - Failures(DV,T\Tt)
= Failures(DV(t),T) - Failures(DV(t),T\Tt)
= |{(x, c(x)) ∈ DV(t) : c(x) ≠ CDT(x,root(T))}|
- |{(x, c(x)) ∈ DV(t) : c(x) ≠ label(t)}|
Uwe Bubeck
Machine Learning: Decision Trees
4
2
Reduced Error Pruning 3/4
∆Failures(t) =
|{(x, c(x)) ∈ DV(t) : c(x) ≠ CDT(x,root(T))}|
- |{(x, c(x)) ∈ DV(t) : c(x) ≠ label(t)}|
Hier: label(t) = No
(aus D(t) ! vgl. Folie 1)
outlook
overcast
sunny
rain
yes
wind
temp.
strong
weak
yes
cool
yes
no
hot
no
t
mild
wind
weak
Tt
no
strong
yes
CDT((D16, ...),root(T)) = Yes
CDT((D20, ...),root(T)) = Yes
∆Failures(t) = |{(D16,...), (D20,...)}| - |{}| = 2
Uwe Bubeck
Machine Learning: Decision Trees
5
Reduced Error Pruning 4/4
Verbesserungspotentiale der anderen Knoten:
outlook ∆Failures(t) = 0
overcast
rain
yes
∆Failures(t) = 0
weak
yes
sunny
wind
temp.
strong
no
cool
yes
hot
no
∆Failures(t) = 2
mild
wind
weak
no
∆Failures(t) = 1
strong
yes
→ Pruning des Knotens temp.
→ Aktualisierung von ∆Failures(t) auf den betroffenen Pfaden.
→ Fortsetzung, bis ∆Failures(t) < 0 für alle Knoten t.
Uwe Bubeck
Machine Learning: Decision Trees
6
3