121 200607 LK Math Klausur1 Aufgaben

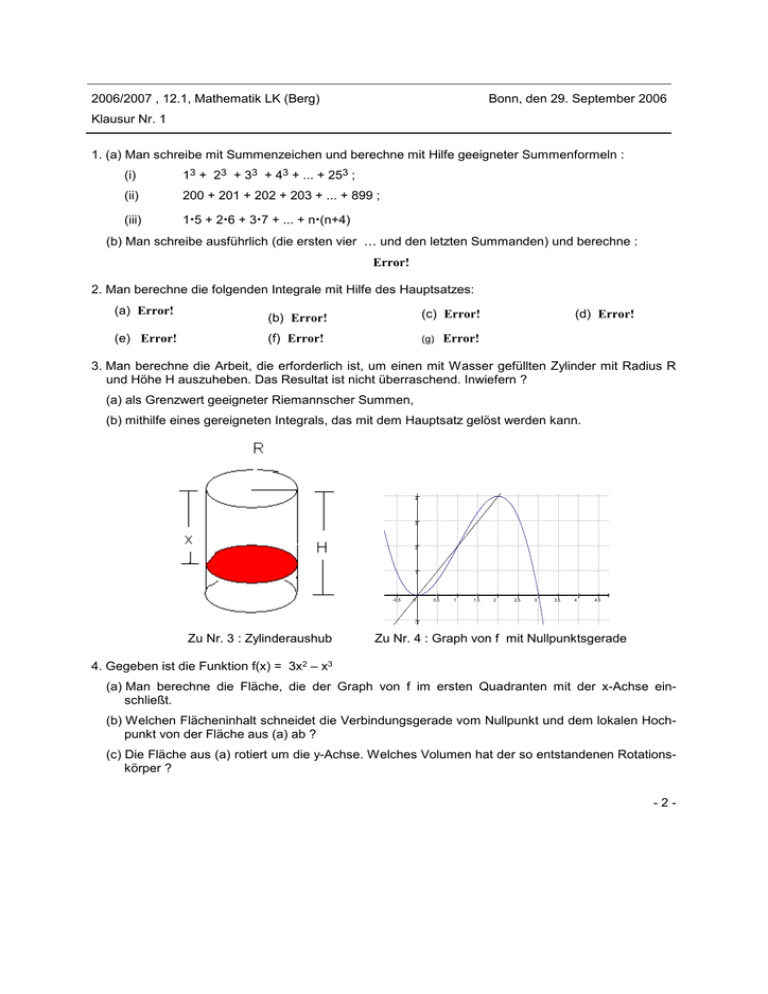
2006/2007 , 12.1, Mathematik LK (Berg)
Bonn, den 29. September 2006
Klausur Nr. 1
1. (a) Man schreibe mit Summenzeichen und berechne mit Hilfe geeigneter Summenformeln :
(i)
13 + 23 + 33 + 43 + ... + 253 ;
(ii)
200 + 201 + 202 + 203 + ... + 899 ;
(iii)
1.5 + 2.6 + 3.7 + ... + n.(n+4)
(b) Man schreibe ausführlich (die ersten vier … und den letzten Summanden) und berechne :
Error!
2. Man berechne die folgenden Integrale mit Hilfe des Hauptsatzes:
(a) Error!
(e) Error!
(b) Error!
(c) Error!
(f) Error!
(g)
(d) Error!
Error!
3. Man berechne die Arbeit, die erforderlich ist, um einen mit Wasser gefüllten Zylinder mit Radius R
und Höhe H auszuheben. Das Resultat ist nicht überraschend. Inwiefern ?
(a) als Grenzwert geeigneter Riemannscher Summen,
(b) mithilfe eines gereigneten Integrals, das mit dem Hauptsatz gelöst werden kann.
y
4
3
2
1
x
-4.5
-4
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
-1
Zu Nr. 3 : Zylinderaushub
Zu Nr. 4 : Graph von f mit Nullpunktsgerade
-2
4. Gegeben ist die Funktion f(x) = 3x2 – x3
-3
(a) Man berechne die Fläche, die der Graph von f im ersten Quadranten mit der x-Achse einschließt.
-4
(b) Welchen Flächeninhalt schneidet die Verbindungsgerade vom Nullpunkt und dem lokalen Hochpunkt von der Fläche aus (a) ab ?
(c) Die Fläche aus (a) rotiert um die y-Achse. Welches Volumen hat der so entstandenen Rotationskörper ?
-2-
2006 / 2007 12.1 Mathematik LK, Klausur 1, Seite 2
5. Logarithmus- und Exponentialfunktion
(a) Wie wird der natürliche Logarithmus ln x nach Felix Klein definiert und was bedeutet diese Definition für die Ableitung von ln x ?
(b) Es sei a eine Konstante. Man leite f(x) = ln (ax) ab (Kettenregel !). Inwiefern folgt aus dem Ergebnis die Logarithmenregel ln ab = ln a + ln b ?
(c) Im Unterricht haben wir Näherungsformeln für ln x erarbeitet. Bestimmen Sie ln 11 mit diesen
Näherungsformeln für n = 1000. Wie genau ist diese Näherung ?
(d) Man berechne den Flächeninhalt eines Sehnentrapezes über der Hyperbel y = Error! zwischen
den Randwerten a und b (beide positiv mit a < b) und zeige, dass diese nur vom Quotient der
Randwerte abhängt. Benutzen Sie diese Tatsache, um einen Teil der Näherungsformeln (2) (s.
Ergänzung zur Formelsammlung) herzuleiten.
(2) 2n Error!
 ln x  Error! (Error!
-
Error!)
Sehnentrapez
(e) Man berechne ln 11 für n = 1000 mithilfe der Näherungsformeln (2) und vergleiche mit der Genauigkeit aus (c).
(f ) Man benutze die linke Seite von (2) um eine Näherungsformel für die Eulersche Zahl e zu berechnen. Welcher Näherungswert ergibt sich speziell für n = 1000. Man vergleiche die Genauigkeit mit der bekannten Näherung.