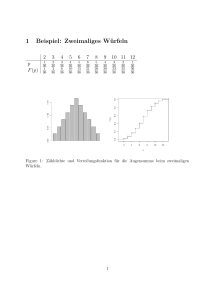
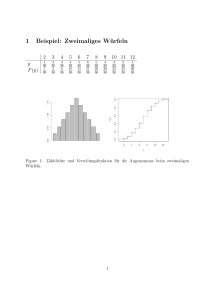
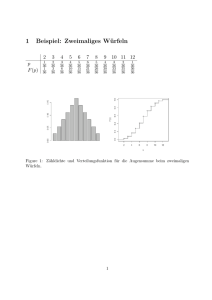
3. Übungen zu Mathematische Methoden der Physik 1 / 8. April

3. Übungen zu Mathematische Methoden der Physik 1 / 8. April 2002
Wahrscheinlichkeit
1. Ein W-maß der reellen Achse R, die Exponentialverteilung, hat die Dichte ρ(x) = λ exp (−λx) für
x > 0 und ρ(x) = 0 sonst.
(a) Welches W-maß hat das Intervall (a, b)? limb→∞ W ((0, b)) =?
(b) Welchen Erwartungswert und welche Varianz hat die stochastische Variable X(x) := x?
p
(c) Welche Verteilungsfunktion
F o´
und Dichte F 0 hat die stochastische Variable |X|? Hinweis:
³n
p
F (ξ) = W
x ∈ R | |x| ≤ ξ . Skizzieren Sie die Graphen von F und F 0 .
(d) Sei B das Ereignis B = (L, ∞) mit gegebenem L > 0. Welche Verteilungsfunktion und Dichte
hat die Einschränkung von X − L auf B unter dem konditionellen W-maß WB ?
(e) Welche relative Wahrscheinlichkeit hat das Ereignis A = (0, L1 ) bezüglich B = (0, L2 )? Sind
diese Ereignisse unabhängig?
ª
©
2. Das W-maß W von R3 , sei für R > 0 in (x, y, z) ∈ R3 | x2 + y 2 + z 2 < R2 gleichverteilt.
(a) Welche Verteilungsfunktion und Dichte hat (die stochastische Variable) r unter W ?
p
r : R3 → R,
r(x, y, z) := x2 + y 2 + z 2
(b) hriW =?, VW (r) =?
(c) Welche Verteilungsfunktion hat π1 : (x, y, z) 7→ x unter W ?
3. Der Abstand r zwischen Kern und Elektron eines H-Atoms hat im Grundzustand die Verteilungsfunktion F : R>0 → R mit
Z x
ρ(ξ)dξ,
ρ(x) := N x2 exp(−x).
F (x) :=
0
(Hier ist der halbe Bohrsche Radius als Längeneinheit gewählt.) N ∈ R
(a) N =? Hinweis: limx→∞ F (x) = 1.
(b) Skizzieren Sie die Graphen von F und ρ.
(c) hri =?, V (r) =?
1