wahrscheinlichkeitstheorie und statistik für studierende der informatik

8 Verteilungsfunktionen und Dichten
8.1 Satz und Definition (Dichten)
Eine Funktion f : R → R heißt Dichtefunktion, kurz Dichte, wenn sie (Riemann-)
integrierbar ist mit f (t) ≥ 0 für alle t ∈ R und
Z
∞
f (t) dt = 1.
−∞
Setzt man
P(B) :=
Z
f (t) dt,
B ⊂ R,
B
so ist P ein Wahrscheinlichkeitsmaß auf R, welches als die zur Dichte f gehörende
Verteilung bezeichnet wird.
Die Dichten dürfen nicht mit den Zähldichten verwechselt werden!
Ist B ein Intervall, etwa B = (a, b], so kann
(erweiterte) Riemann-Integral ersetzen werden:
R
B
f (t) dt durch das gewöhnliche
P([a, b]) = P((a, b]) = P([a, b)) = P((a, b))
Z b
=
f (t) dt, −∞ ≤ a < b ≤ ∞
a
Anschaulich: P([a, b]) ist die Fläche unter der Dichtefunktion f zwischen den Grenzen a und b.
Dichte und Wahrscheinlichkeit
Achtung: Die Dichte f ist nicht eindeutig bestimmt. f darf in endlich vielen Punkten
beliebig geändert werden, ohne dass sich die Integrale ändern.
Voraussetzung: Im Folgenden setzten wir voraus, dass die Dichten f bis auf endlich
viele Stellen stetig sind.
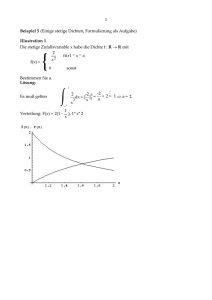
8.2 Beispiel
Gleichverteilung auf dem Intervall (a, b)
Die zur Dichte (−∞ < a < b < ∞)
1
, a<t<b
b−a
f (t) =
 0 , sonst


gehörende Verteilung heißt (stetige) Gleichverteilung U(a, b) (auf dem Intervall
(a, b)). Hierbei steht U für uniform“.
”
f (t)
1.0
0.8
0.6
0.4
0.2
0
1
2
t
8.3 Satz und Definition
Stetige Zufallsvariablen
Eine Zufallsvariable X heißt stetig (verteilt), wenn es eine Dichte fX gibt mit
P(a ≤ X ≤ b) =
Z
b
fX (t) dt
a
für alle a, b mit −∞ ≤ a < b ≤ ∞.
In diesem Fall heißt die Funktion fX (eine) (Riemann-) Dichte von X, und PX ist
dann die zu fX gehörende Verteilung.
8.4 (Bemerkungen:)
a) Ist die Zufallsvariable X stetig, so gilt
P(X = t) = 0
für jedes t ∈ R, insbesondere
P(a < X ≤ b) = P(a ≤ X < b)
= P(a < X < b) =
Z
b
fX (t) dt
a
für alle a, b mit −∞ ≤ a < b ≤ ∞.
b) Ist X stetig und a eine Stetigkeitsstelle von fX , so gilt für genügend kleines
ǫ>0
P(a < X < a + ǫ) ≈ fX (a) · ǫ,
P(a − ǫ < X < a + ǫ) ≈ fX (a) · 2ǫ.
Dabei kann jedes der Kleiner-Zeichen durch ≤“ ersetzt werden.
”
Zur Interpretation von f (a)
8.5 Definition (Verteilungsfunktion)
Ist P ein (beliebiges) Wahrscheinlichkeitsmaß auf R, so heißt die Funktion
F (t) :



 R −→ [0, 1]


 t
7−→ F (t) := P((−∞, t])
die Verteilungsfunktion von P.
Ist speziell X eine Zufallsvariable mit Verteilung PX , so heißt die Verteilungsfunktion
von PX auch Verteilungsfunktion von X. Diese wird mit FX bezeichnet, und es gilt
FX (t) = P(X ∈ (−∞, t]) = P(X ≤ t), t ∈ R.
8.6 Beispiel
Die Gleichverteilung U(a, b) auf dem Intervall (a, b) besitzt die Verteilungsfunktion
F (t) =



 0
t−a
b−a


 1
1.0
0.8
0.6
0.4
0.2
0
, t ≤ a,
, a < t ≤ b,
, t > b.
F (t)
1
2
Verteilungsfunktion von U(1, 2)
t
8.7 Satz
Jede Verteilungsfunktion F besitzt die folgenden Eigenschaften:
a) F ist monoton wachsend, d.h. aus s ≤ t folgt F (s) ≤ F (t).
b) F ist rechtsseitig stetig, d.h. es gilt
lims>t,s→t F (s) = F (t)
für alle t ∈ R.
c) F (−∞) := limt→−∞ F (t) = 0 und F (∞) := limt→∞ F (t) = 1.
8.8 Satz
Aus
P({X ≤ b}) = P({X ≤ a} + {a < X ≤ b}) = P(X ≤ a) + P(a < X ≤ b)
folgt für beliebige Zufallsvariablen X
P(a < X ≤ b) = FX (b) − FX (a)
für −∞ ≤ a < b ≤ ∞, insbesondere
P(X > t) = 1 − FX (t), t ∈ R.
Für stetige Zufallsvariablen X gilt darüber hinaus
P(a ≤ X ≤ b) = P(a < X < b)
= P(a ≤ X < b) = FX (b) − FX (a)
für alle −∞ < a < b < ∞. Ist X diskret mit Werten in 0, 1, 2, . . . und der Zähldichte fX , so gilt
X
FX (t) =
fX (k), t ∈ R.
k≤t
FX ist in diesem Fall eine Treppenfunktion.
Besitzt dagegen X die Dichte fX , so gilt
FX (t) =
Z
t
fX (x) dx, t ∈ R.
−∞
In diesem Fall ist FX stetig.
Dichte und Verteilungsfunktion bei diskreter und stetiger Verteilung
8.9 Satz
Ist die Verteilungsfunktion FX von X stetig und bis auf endlich viele Stellen stetig
differenzierbar, so ist die Funtion fX (x) mit
fX (x) := FX′ (x)
falls FX in x stetig differenzierbar ist und mit fX (x) = 0 sonst, eine Dichte von X.
8.10 Definition (Mehrdimensionale Dichten)
Eine Funktion f : Rn → R ist eine Dichte, wenn sie (erweitert Riemann-) integrierbar ist mit f (t) ≥ 0 für alle t ∈ Rn und
Z
Z ∞ Z ∞
f (t) dt =
...
f (t1 , . . . , tn ) dtn . . . dt1 = 1.
Rn
−∞
−∞
Durch
P(B) =
Z
f (t) dt, B ∈ Bn ,
B
ist ein Wahrscheinlichkeitsmaß P auf Bn definiert, die zu f gehörende Verteilung.
Sonderfälle
Ist B = {(s, t) ∈ R2 : a ≤ s ≤ b , g(s) ≤ t ≤ h(s)} mit stetigen Funktionen g
und h, wobei g ≤ h, so gilt
Z
f (s, t) d(s, t) =
B
a
insbesondere im Fall
Z
B
Z b "Z
h(s)
#
f (s, t)dt ds,
g(s)
B = {(s, t) ∈ R2 : a ≤ s ≤ b , c ≤ t ≤ d}
f (s, t) d(s, t) =
Z b Z
a
c
d
Z
f (s, t)dt ds =
d
c
Z
a
b
f (s, t)ds dt.
5
0
4
-5
2
3
-10
-4
1
-3
0
-2
-2
1
t
0
2
-3
s
-1
-1
3
4
-4
f (s ,t )
10
Wahrscheinlichkeit als Volumen
8.11 Beispiel
Die (stetige) Gleichverteilung UC auf einer Menge C ⊂ R2 mit positivem, endlichen
Flächeninhalt c (0 < c < ∞) ist das Wahrscheinlichkeitsmaß mit der Dichte
f (s, t) =
(
1/c , falls (s, t) ∈ C,
0
, sonst.
Es gilt dann
UC (B) =
Fläche von B ∩ C
, B ⊂ R2 .
Fläche von C
8.12 Definition
Sind X und Y stetige Zufallsvariablen mit
P(a ≤ X ≤ b, c ≤ Y ≤ d) =
Z b Z
a
c
d
fX,Y (s, t) dt ds
für −∞ ≤ a < b ≤ ∞, −∞ ≤ c < d ≤ ∞ für eine Riemann-integrierbare Funktion
fX,Y : R2 → R≥0 , so heißt fX,Y (eine) gemeinsame Dichte von X und Y .
Die zu fX,Y gehörende Verteilung ist dann die gemeinsame Verteilung PX,Y von X
und Y .
8.13 Satz (Marginalverteilungen)
Sind X und Y stetige Zufallsvariablen mit gemeinsamer Dichte fX,Y , so ist
s → fX (s) :=
Z
∞
fX,Y (s, t) dt
−∞
eine Dichte von X und
t → fY (t) :=
eine Dichte von Y .
Z
∞
fX,Y (s, t) ds
−∞